Class 10

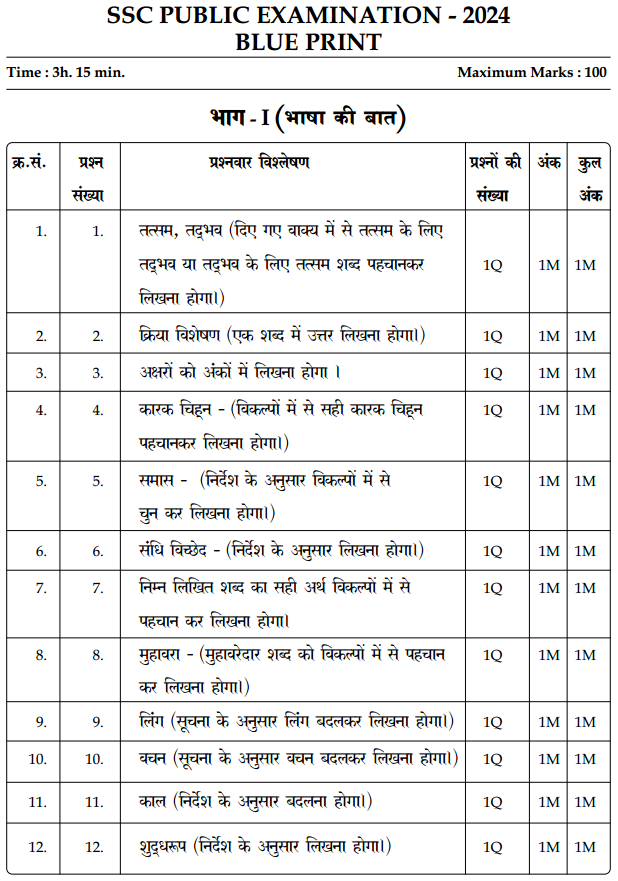
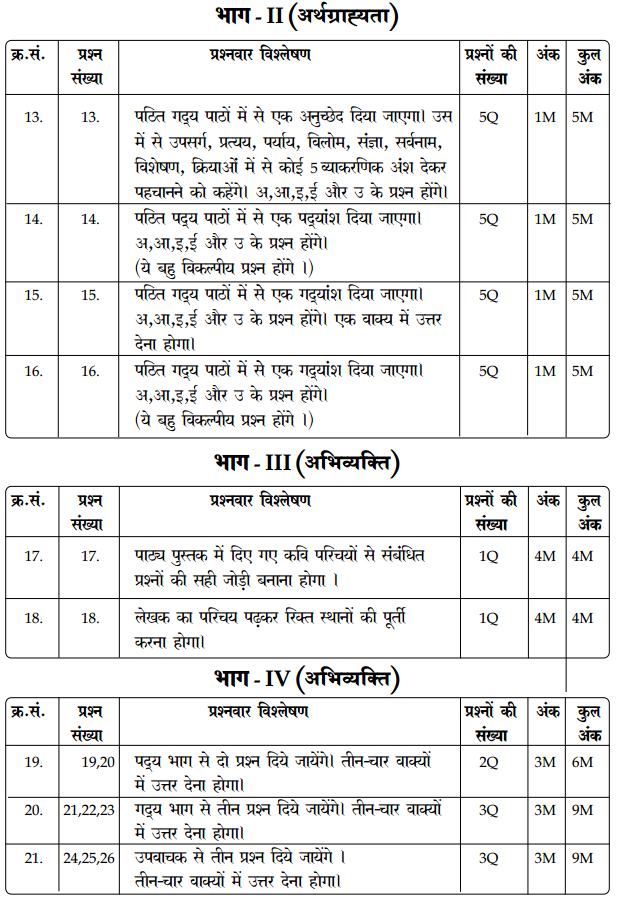
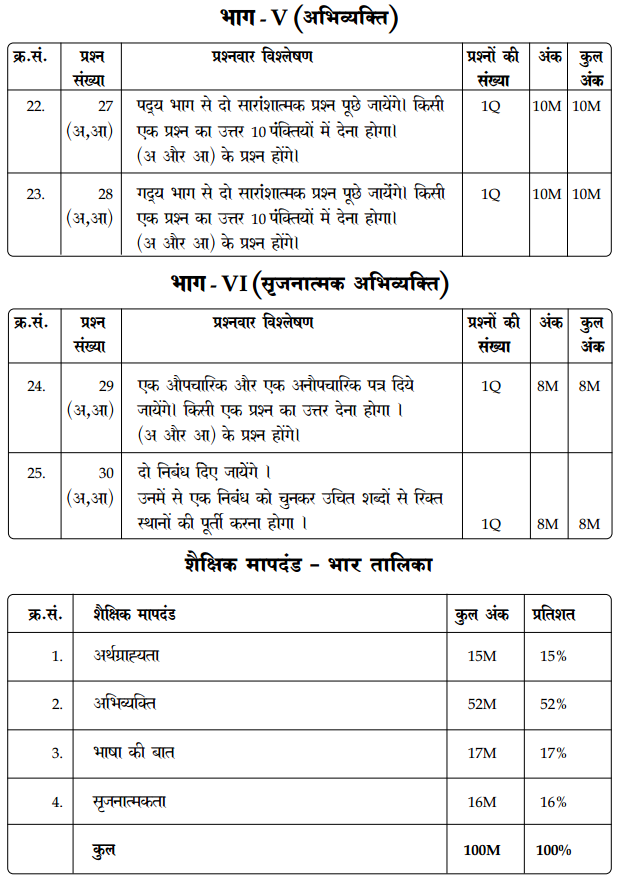
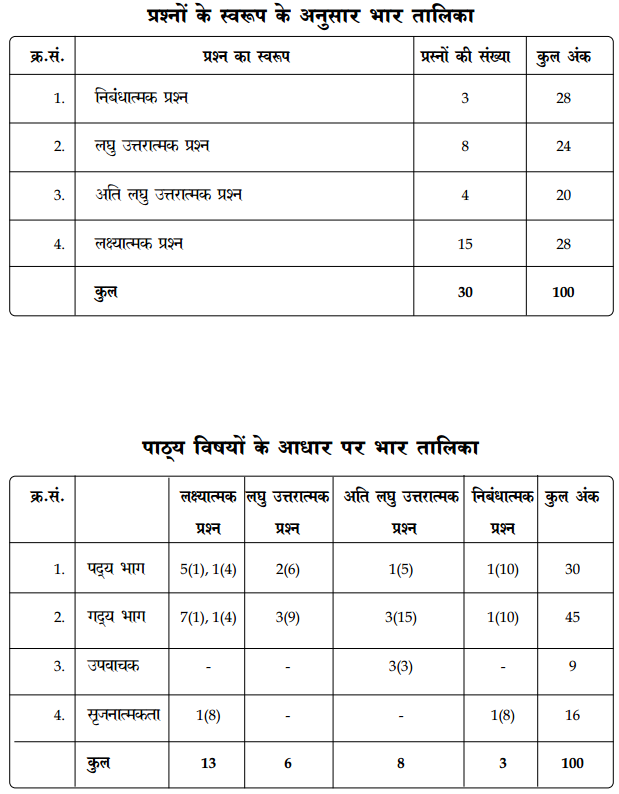
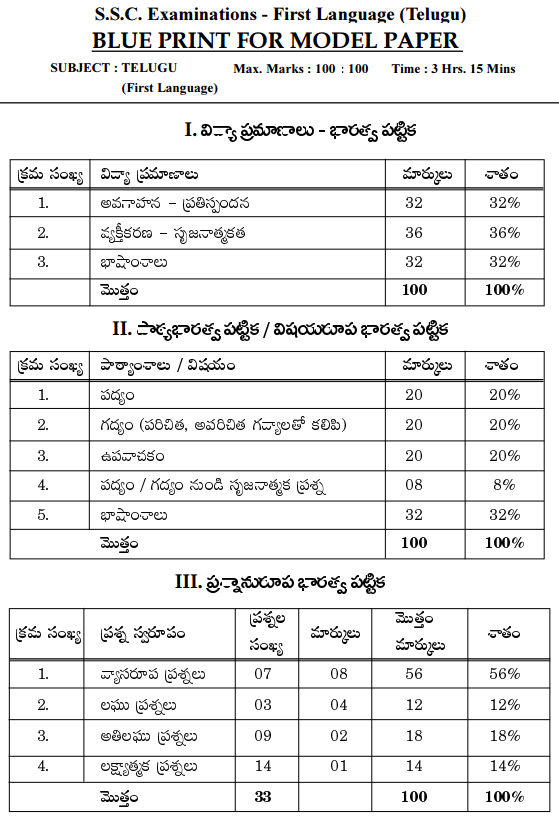
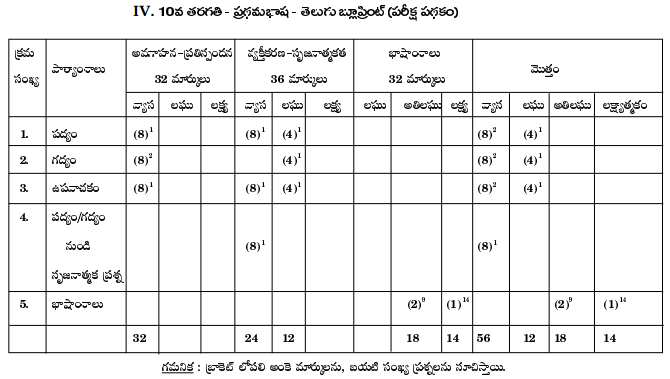
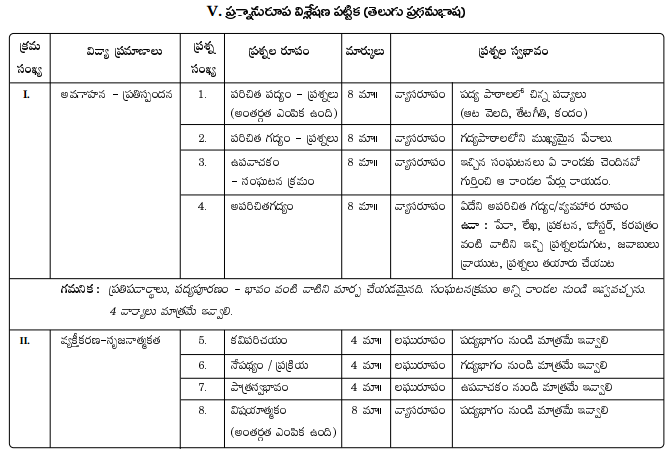
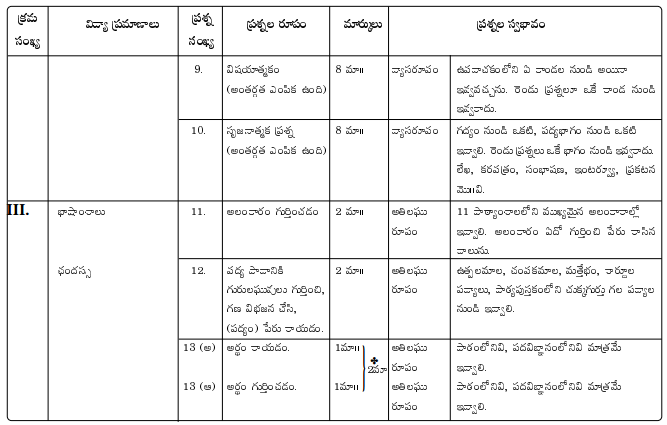
Reviewing TS 10th Class Telugu Model Papers and TS 10th Class Telugu (S/L) Question Paper April 2023 can help students identify areas where they need improvement.

TS 10th Class Telugu (S/L) Question Paper April 2023

‘సమయం: 2 గం. 30 ని.లు
మార్కులు : 60

విద్యార్థులకు సూచనలు :

1. జవాబులు రాయడానికి 2 గంటల 30 నిముషాలు ఉపయోగించాలి.
2. పార్ట్ ‘బి’ చివరి 30 నిమిషాలలో పూర్తిచేసి, పార్ట్ ‘ఎ’ జవాబు పత్రానికి జతచేయాలి.

పార్ట్ – A
I. అవగాహన – ప్రతిస్పందన (20 మార్కులు)

అ) కింది, పేరా చదువండి. ఇచ్చిన ప్రశ్నలకు జవాబులు 1, 2 వాక్యాలలో రాయండి. (5 × 1 = 5 మా.)

వ్యాపారస్తుడు రంగడి రిక్షా ఎక్కుతూ, “చౌరస్తాకు తీసుకువెళ్ళు” అన్నాడు. అతను చౌరస్తాలో దిగి రంగడి చేతిలో నాలుగణాల బిళ్ళ పెట్టి వెళ్ళిపోయాడు. రంగడు ఇంటికి చేరుకుని రిక్షా మూలకు చేరుస్తుండగా రిక్షాలోంచి ఒక బరువు గల సంచి కిందపడింది. మిణుగు మిణుగుమంటున్న దీపాన్ని పెద్దది చేసి, సంచిని చేతిలో పట్టుకుని లోనికెళ్ళి తెరిచి చూశాడు. సంచి నిండా ముత్యాలున్నాయి. చౌరస్తాలో రిక్షా దిగి వెళ్ళిన వ్యక్తి ముత్యాల వర్తకుడనీ, అతడే సంచి మరిచిపోయి ఉంటాడనీ రంగడు నిశ్చయించుకున్నాడు.

ప్రశ్నలు :

ప్రశ్న 1.
రంగడి రిక్షా ఎవరు ఎక్కారు ?
జవాబు:
వ్యాపారస్తుడు

ప్రశ్న 2.
రిక్షాలోంచి ఏమి పడింది ?
జవాబు:
బరువు గల ఒక సంచి.

ప్రశ్న 3.
సంచిలో ఏమి ఉన్నాయి ?
జవాబు:
ముత్యాలు

ప్రశ్న 4.
రంగడు ఏమని నిశ్చయించుకున్నాడు ?
జవాబు:
చౌరస్తాలో రిక్షా దిగి వెళ్ళిన వ్యక్తి ముత్యాల వర్తకుడనీ, అతడే సంచి మరచిపోయి ఉంటాడనీ రంగడు నిశ్చయించుకున్నాడు.

ప్రశ్న 5.
వ్యాపారస్తుడు రంగడి చేతిలో ఏమి పెట్టాడు
జవాబు:
నాలుగణాల బిళ్ళ

ఆ) కింది పద్యాలలో ఏదైనా ఒక పద్యానికి ప్రతిపదార్థం రాయండి. (1 × 5 = 5 మా.)

ప్రశ్న 6.
సత్యం బెప్పుడు ……….. సర్వేశ్వరా !
జవాబు:
సత్యం బెప్పుడు తప్పఁడేనియు, దురాచారుండు గాఁడేని, యౌ
చిత్యం చేమఱఁడేని, దుర్జనుల గోష్ఠిం బొందఁడే భక్త సాం
గత్యం బాదటఁ బాయఁడేని మదనగ్రస్తుండు గాఁడేని నీ
భృత్యుం డాతఁడు మూఁడు లోకములలోఁ బూజ్యుండు సర్వేశ్వరా !

(లేదా)

సిరిగల వాని కెయ్యెడల ……….. ఫలంబు భాస్కరా !
జవాబు:
సిరిగల వాని కెయ్యెడల జేసిన మేలది నిష్ఫలంబగున్
నెఱిగురిగాదు పేదలకు నేర్పున జేసిన సత్ఫలంబగున్
వఱపున వచ్చి యేఘుడొక వర్షము వాడిన చేలమీదటన్
కురిసిన గాక యంబుధులు గుర్వగనేమి ఫలంబు భాస్కరా !

ఇ) కింది గద్యాన్ని చదువండి. ప్రశ్నలను తయారు చేయండి. (5 × 2 = 10 మా.)

గోలకొండ కోటను గొర్రెల కాపరుల కొండ అని పిలిచేవారు. అదే గొల్లకొండ, గోల్కొండగా మారింది. ఇది తెలంగాణాలో హైదరాబాద్లో ఉన్నది. గోల్కొండ కోట నిర్మాణం జరిగి దాదాపు 500 సంవత్సరాలు గడిచాయి. ఎన్ని విపత్తులు వచ్చినా, ఎన్ని రాజ్యాలు దండెత్తినా తట్టుకొని నిలబడింది. ఈ కోట 10 కిలోమీటర్ల పరిధిలో 87 చంద్రాకార బురుజులు ఉన్నాయి. 8 ప్రధాన ద్వారాలూ, నాలుగు వంతెనలు, అనేక రాజ మందిరాలూ, ఆలయాలూ, మసీదులతో నేటికీ ఎంతో వైభవంగా కనిపిస్తున్నది.

ప్రశ్న 7.
……………………………….
జవాబు:
గోలకొండను ఏమని పిలిచేవారు ?

ప్రశ్న 8.
………………………………
జవాబు:
గొల్లకొండ ఎలా మారింది ?

ప్రశ్న 9.
………………………………
జవాబు:
గోల్కొండ ఏ రాష్ట్రంలో ఉంది ?

ప్రశ్న 10.
………………………….
జవాబు:
గోల్కొండ కోట నిర్మాణ ప్రత్యేకత ఏమిటి ?

ప్రశ్న 11.
…………………………
జవాబు:
గోల్కొండ కోట పరిధిలో ఎన్ని బురుజులు ఉన్నాయి ?

II. వ్యక్తీకరణ – సృజనాత్మకత
(32 మార్కులు)

అ) కింది ప్రశ్నలకు 4 నుండి 6 వాక్యాలలో జావాబులు రాయండి. (4 × 4 = 16 మా.)

ప్రశ్న 12.
డాక్టర్ సి. నారాయణరెడ్డి గురించి మీకు తెలిసిన విషయాలు రాయండి.
జవాబు:
సి. నారాయణరెడ్డి 29.07.1931 సం॥రంలో, పూర్వపు కరీంనగర్ జిల్లా నేటి రాజన్న సిరిసిల్ల జిల్లా, హనుమాజీపేట గ్రామంలో జన్మించారు. ఈయన ప్రముఖ కవి. సాహితీ పరిశోధకుడు. బహుభాషావేత్త. ప్రయోగశీలి. నాగార్జునసాగరం, కర్పూర వసంతరాయలు, విశ్వంభర, మధ్యతరగతి మందహాసం, ప్రపంచ పదులు మున్నగు 70కి పైగా కావ్యాలు రాశాడు. భారత ప్రభుత్వంచే ‘పద్మభూషణ్’ పుస్కారంతో సత్కరించబడ్డాడు. ‘విశ్వంభర’ కావ్యానికి జాతీయస్థాయిలో అత్యున్నత స్థాయి సాహితీ పురస్కారమైన ‘జ్ఞానపీఠ్ అవార్డును’ అందుకున్నాడు.

ప్రశ్న 13.
“తేనెటీగ సంపాదించిన తేనె బాటసారి పాలైంది కదా !” మరి మీరు సంపాదించిన ధనాన్ని మీరు ఏమి చేస్తారు ?
జవాబు:
“తేనెటీగ సంపాదించిన తేనె బాటసారి పాలైంది కదా ! కాని నేను కష్టపడి ధనాన్ని సంపాదిస్తాను. కొంత పొదుపుచేసి భవిష్యత్తులో ఉపయోగపడటానికి దాచి ఉంచుతాను. తృప్తిగా తింటాను. మిగిలిన కొంత సొమ్మును సాటి పేద ప్రజలకు పంచి పెడతాను.

ప్రశ్న 14.
“సంస్కృతీ, నాగరికతలకు పునాదులు పల్లెపట్టులు” అని పొడుపు కథలు పాఠంలో ఉన్నది కదా ! ఎట్లాగో రాయండి.
జవాబు:
మన భారతీయ సంస్కృతి ఎంత ప్రాచీనమైందో అంత విచిత్రమైంది. దానికి ఔన్నత్యం ఎంత ఉందో అంత వైశాల్యమూ ఉంది. ఈ రెండింటిని మించిన లోతు కూడా ఉంది. మనది వ్యవసాయిక దేశం. ఈ దేశీయుల సంస్కృతీ నాగరికతలకు పునాదులు పల్లెపట్టులు. మన పూర్వులు ఆ పశుపాలనలో, ఆ పచ్చిక బయళ్ళలో, ఆ నీలాకాశంలోని మెరుపుల్లో, కుండపోతగా కురిసే వానల్లో ఏదో తమకు తెలియని రహస్యం దాగి ఉంది. ఈ భావనే అన్ని తత్వ రహస్యాలకూ, సమస్యలకూ, ముడులకూ, ముడి విప్పులకూ కారణమైంది.

ప్రశ్న 15.
చదువు మన జీవిత గమనాన్ని ఏ విదంగా మారుస్తుందో మీ మాటల్లో రాయండి.
జవాబు:
మనం చిన్నప్పుడు చదువుకున్న చదువు మన జీవిత గమనాన్ని మారుస్తుంది. ఆవేశాలను అణగారుస్తుంది. ఆలోచనలను రేకెత్తిస్తుంది. మానవులంగా సమానమే అన్న భావన కలిగిస్తుంది. అన్ని వర్గాల వాళ్ళకూ సామాజిక భాగస్వామ్యం మరియు చైతన్యం ఎంతో అవసరమని తెలియజేస్తుంది. ప్రతి ఒక్కరిలోను చైతన్యం రావాలి అంటే చదువుకోవాలి. నిరక్షరాస్యతను నిర్మూలించాలి. చదువు అక్షరాస్యతను అభివృద్ధి చేయటానికి మార్గాలను అన్వేషించేటట్లు చేస్తుంది. ప్రతి ఒక్కరూ అన్ని వర్గాల వారికి చదువు ప్రాధాన్యతను వివరించి, వారిని ఉత్తేజపరచడానికి నడుం బిగించాలి.

ఆ) కింది ప్రశ్నలకు పది వాక్యాలలో జవాబులు రాయండి. (2 × 8 = 16 మా.)

ప్రశ్న 16.
“ఎంత పీల్చినా గాలికి ఎప్పుడైనా కోత ఉన్నదా.” అని కవి ఎందుకన్నాడో వివరించండి.
జవాబు:
“తరతరాలుగా మట్టిని దున్నుతున్నప్పటికినీ అది బాధపడదు. అలాగే ఎల్లప్పుడూ పరవళ్ళు తొక్కుతూ ప్రవహించే ఏటికి కూడా అనారోగ్యం ఉండదు. కనుక ఈ కొద్ది ప్రయాణానికే అలసిపోయే మానవులారా ! ఆలోచించుకోండి. ఎంత ఎత్తుకు ఎగిరినప్పటికీ ఆకాశానికి అంతు ఉండదు. ప్రాణికోటి ఎంత పీల్చుకుంటున్నా గాలికి కరవు ఉండదు. మనిషి కూడా ఇటువంటి చైతన్యంతో ఉన్నతమైన లక్ష్యం కోసం కృషి చేయాలి.

(లేదా)

శతక పద్యాలు చదవడం వల్ల ఏయే లక్షణాలు పెంపొందుతాయి ?
జవాబు:
శతక పద్యాలను ప్రతి ఒక్కరూ నేర్చుకోవాలి. ఇవి లోకంలో మంచి చెడులను, లోక ధర్మాలను, లోక రీతుల్ని తెలియజేస్తాయి. ప్రతి ఒక్కరిలో నైతిక విలువలను పెంపొందిస్తాయి. బాలబాలికల్ని ఉత్తమ పౌరులుగా తీర్చిదిద్దుతాయి. సమాజానికి హితం చేస్తాయి. నీతి, ధర్మం, సత్యం, దేశభక్తి, మంచి నడవడి మొదలైనవి శతక పద్యాలు బోధిస్తాయి. ‘పైగా శతక పద్యాల్లో ఎన్నో నీతులు, విలువలు చోటు చేసుకున్నాయి. అందరిలో ఆ విలువల్ని పెంపొందింపచేయడమే శతక పద్యాల గొప్పదనం. కనుక వాటిని ఆచరించాలి.

ప్రశ్న 17.
భాగ్యరెడ్డి వర్మ మంచి నాయకుడిగా పేరు తెచ్చుకున్నాడు కదా ! మీకు కూడా మంచి పేరు రావాలంటే మీరు ఏమి చెయ్యాలనుకుంటున్నారో రాయండి.
జవాబు:
అంటరాని వర్గాలు అనుభవిస్తున్న అవస్థల నుంచి వారిని గట్టెక్కించడానికి భాగ్యరెడ్డి వర్మ అంకిత భావంతో కృషి చేశాడు కదా ! నేను కూడా అణగారిన కులాల నాయకుల సహకారం, నైతిక మద్దతు కూడగట్టుతాను. అంటరాని వర్గాల ఉన్నతి కోసం సంస్కరణలు మొదలుపెడతాను. మనుషులు సమానమని, ఎవరూ ఎక్కువ, తక్కువ కాదన సత్యాన్ని తెలుసుకునేటట్లు చేస్తాను. అంటరాని వర్గాలు, చదువుపై చూపు పెట్టేటట్లు చేస్తాను. అందువల్ల కొన్ని సాంఘిక దురాచారాలు మటుమాయమవుతాయి. అనేక బహిరంగ సభలు జరిపి, సామాజిక స్వచ్ఛత గురించి చెప్పి, వారందరినీ ఏకతాటిపై నడిపిస్తాను. దేవదాసి, ముర్లీ, వేశ్యా సంప్రదాయాలను అడ్డుకుంటాను. ప్రజలచే తాగుడు మాన్పిస్తాను, అణగారిన వార్గల్లో చేతన్యాన్ని తేవడానికి కృషి చేస్తాను.

(లేదా)

“తెలుగు మహిళ” పాఠం చదివారు కదా ! తల్లి తమ సంతానానికి ఏ విధమైన ఆదర్శాలు బోధిస్తుందో వివరించండి.
జవాబు:
మన జాతి సంస్కృతినీ, నాగరికతనూ అనేక విపత్కరమైన పరిస్థితులలో మన స్త్రీలు కాపాడినారు. వారు పరంపరాగతమైన సదాచారాలనూ, అనుశ్రుతంగా వస్తున్న అలవాట్లనూ పట్టుదలతో, దీక్షతో ఆచరిస్తున్నందువల్లనే మన జాతి సంస్కృతీ, నాగరికత సంరక్షించబడ్డాయి. స్త్రీలు తమ ఆదర్శాలను సాధించడానికి పట్టుదలతో, భక్తిశ్రద్ధలతో, దీక్షతో నోములో, వ్రతాలలో ఆచరించి ఒక విశిష్టమైన శారీరక మానసిక క్రమశిక్షణను అలవరచుకున్నారు. ఈ నోములు వ్రతాల ద్వారా స్త్రీలు కోరుకునేది తమ కుటుంబ సౌఖ్యం. వినాయక చవితికి పిల్లలతో విఘ్నేశ్వర పూజ చేయించి పండుగల విశిష్టతను తెలియజేస్తుంది. సంస్కృతి, సంప్రదాయాలను నేర్పుతుంది. పురాణగాథలను చెప్తుంది. మంచి బుద్ధులను, ఆదర్శాలను తెలియజేస్తుంది.

పెద్దల పట్ల వినయ విధేయతలు, భక్తి గౌరవాలు, పేదల పట్ల దయాదాక్షిణ్యాలు, బంధుప్రీతి, అతిథి అభ్యాగతుల సత్కారము మొదలైన సుగుణాలను తల్లి తన సంతానానికి నేర్పుతుంది.

ఇ) సృజనాత్మకత (8 మార్కులు)

అ) కింది ప్రశ్నల్లో ఏదైనా ఒక ప్రశ్నకు జవాబు రాయండి. (1 × 8 = 8 మా.)

ప్రశ్న 18.
“సమాజంలో సాంఘిక దురాచారాలను తొలగించాలి” అనే విషయాన్ని తెలియజేస్తూ పోస్టర్ తయారు చేయండి..
జవాబు:
సాంఘిక దురాచారాలను తొలగించండి

మహాజనులారా !

మన సమాజంలో ఎంతో కాలంగా ఎన్నో సాంఘిక దురాచారాలు పాతుకుపోయాయి. వాటిని మనం గుడ్డిగా నమ్మి పాటిస్తూ వస్తున్నాము. రాజా రామమోహనరాయ్, ఈశ్వరచంద్ర విద్యాసాగర్, కందుకూరి వీరేశలింగం పంతులు గారు వంటి సంఘ సంస్కర్తలు, సతీ సహగమనము, భర్త పోయిన స్త్రీలకు అలంకారాలు తొలగించడం వంటి దురాచారాల నిర్మూలనకు కృషి చేసి, విజయం సాధించారు. మన ఆంధ్రదేశంలో కందుకూరి వీరేశలింగం పంతులుగారు విధవలకు తిరిగి వివాహాలు జరిపించారు. ఎన్నో మూఢాచారాలను వారు నిర్మూలించారు. దయ్యాలు లేవని, భూత వైద్యం అంతా దగా అని వారు నిరూపించారు. శకునాలు, తిథులు మంచివి కావని వాటిని నమ్మేవారికి జాగృతులు కలిగించండి. వరకట్న పిశాచిని తరిమికొట్టండి. అంటరానితనాన్ని నిర్మూలించి, మానవులంతా ఒక్కటేనని ఎలుగెత్తి చాటండి. మానవ సేవయే మాధవ సేవయని తలచి సాటివారికి సహకరించండి.

ఇట్లు,
సాంఘిక దురాచారాల నిర్మూలన సంఘం,
హైదరాబాదు.

ప్రశ్న 19.
సమాజంలో మీకు సేవలందించే వారి గురించి తెలియజేస్తూ మీ మిత్రునికి లేఖ రాయండి.
జవాబు:

కరీంనగర్,
XXXXXX

ప్రియమైన మిత్రునకు,
నమస్కారము.

నేను క్షేమము. నీవు క్షేమమని తలుస్తాను. మా గ్రామ సమాజంలో ఒక సంఘసేవకుడు ఉన్నారు. నిరంతరం ఆయన ప్రజలకు ఏదో ఒక సేవ చేస్తూనే ఉంటారు. ఆయన పేరు ధర్మారావు. పేరుకు తగినట్టే ఆయన సహాయ సహకారాలందిస్తుంటారు. ముఖ్యంగా మా గ్రామానికి మంచినీటి సౌకర్యాన్ని కల్గించారు. రోడ్లు వేయించారు. పాఠశాలలు, ఆసుపత్రులు నిర్మించి ఉచితంగా ప్రజలకు సేవలందిస్తున్నారు. ఇంకా ఖాళీ ప్రదేశాల్లో చెట్లను నాటించి, సంరక్షణ భారాన్ని ఆయనే తీసుకున్నారు. నీకు తెలిసిన సేవలందించే వారుంటే వారిని గురించి వెంటనే తెలియజేస్తూ ఉత్తరం రాయి.
ఉంటా!

ఇట్లు,
నీ ప్రియమిత్రుడు,
కె. విజయ్

చిరునామా :
పి. శివరామ్
10వ తరగతి, ఇం.నెం. 5-3/14.
ఖమ్మం.

ప్రశ్న 20.
మీ పాఠశాలలో మీరు గీసిన చిత్ర ప్రదర్శన కార్యక్రమానికి ఒక చిత్రకారున్ని ఆహ్వానిస్తూ, ఆహ్వాన పత్రాన్ని తయారు చేయండి.
జవాబు:

శారదా విజ్ఞాన మందిరం
ఆదిలాబాద్
* ఆహ్వానం *

సుప్రసిద్ధ చిత్రకారులగు శ్రీమాన్ రవి గార్కి,
నమస్కారము !
అయ్యా! ‘

ఇటీవల మా పాఠశాలలో మా బాల బాలికలచే చిత్రాలు గీయించి, చిత్రప్రదర్శన ఏర్పాటు చేశాము. దయచేసి మీరు మా పాఠశాలకు వచ్చి, చిత్ర ప్రదర్శనను తిలకించవలసిందిగా ప్రార్థన, అంతేగాక ఆ చిత్ర ప్రదర్శనలో విజేతలైన వారికి బహుమతి ప్రదానం చేయవలసిందిగా ఆహ్వానిస్తున్నాము. మీ అమూల్యమైన సందేశాన్ని ఈయవలసిందిగాను కోరుచున్నాము.
తేది: X X X X X

ఇట్లు,
కార్యదర్శి,
చిత్ర ప్రదర్శన పరిషత్.

పార్ట్ – B

సమయం : 30ని.లు
(మార్కులు : 20)

సూచనలు :

1. అన్ని ప్రశ్నలకు సమాధానాలు నిర్దేశించిన స్థలంలోనే రాయాలి.
2. పూర్తి చేసిన పార్టు – బి పత్రాన్ని పార్టు – ఎ సమాధాన పత్రంతో జతపరచండి.

I. భాషాంశాలు

అ) పదజాలం : (10 మార్కులు)

కింది పదాలను ఉపయోగించి సొంత వాక్యాలు రాయండి. (2 × 1 = 2 మా.)

ప్రశ్న 1.
ఉల్లాసం : ……………………..
జవాబు:
ఉల్లాసం : ఎవ్వరైనా ఎప్పుడూ ఉల్లాసంగా జీవించాలి.

ప్రశ్న 2.
సఖుడు : ………………..
జవాబు:
సఖుడు : అర్జునుడు శ్రీకృష్ణుని సఖుడు.

కింది ప్రశ్నలకు సరైన జవాబును గుర్తించి (A/B/C/D) సంకేతాన్ని బ్రాకెట్లలో రాయండి. (8 × 1 = 8 మా.)

ప్రశ్న 3.
జంతువులపై కరుణ చూపాలి. (గీత గీసిన పదానికి అర్థం)
A) దానం
B) దయ
C) దశ
D) దర్శనం’
జవాబు:
B) దయ

ప్రశ్న 4.
ప్రతి వ్యక్తి ఓ లక్ష్యముతో పని చేయాలి. (గీత గీసిన పదానికి అర్థం)
A) యుద్ధం
B) శబ్దం
C) గురి
D) ఎల్లప్పుడు
జవాబు:
C) గురి

ప్రశ్న 5.
‘అంబుధి’ లో నీరు ఉప్పగా ఉంటుంది. (గీత గీసిన పదానికి పర్యాయపదాలు)
A) ఆకాశం, గగనం
B) గృహం, నిలయం
C) మాట, పలుకు
D) సముద్రం, సంద్రం
జవాబు:
D) సముద్రం, సంద్రం

ప్రశ్న 6.
ఎండాకాలం పయస్సును ఎక్కువగా వాడుతాము. (గీత గీసిన పదానికి పర్యాయపదాలు)
A) పాలు, క్షీరము
B) నీరు, ఉదకము
C) పరమాన్నం, పాయసం
D) చారు, రసం
జవాబు:
A) పాలు, క్షీరము

ప్రశ్న 7.
“కుడుచు’ పదానికి నానార్థాలు గుర్తించండి.
A) తిను, తాగు
B) గుహ, అడవి
C) తామర, శంఖం
D) మేఘం, చీకటి
జవాబు:
A) తిను, తాగు

ప్రశ్న 8.
“సంతోషం, స్నేహం” నానార్థాలుగా గల పదం
A) కోతి
B) మూతి
C) ప్రీతి
D) నూతి
జవాబు:
C) ప్రీతి

ప్రశ్న 9.
‘పుస్తకం’ పదానికి వికృతి పదం
A) బాస
B) పానం
C) బత్తి
D) పొత్తం
జవాబు:
D) పొత్తం

ప్రశ్న 10.
“కస్తి” పదానికి ప్రకృతి పదం
A) కష్టం
B) కథ
C) ఆధారం
D) గుణం.
జవాబు:
A) కష్టం

ఆ) వ్యాకరణాంశాలు: (10 మార్కులు)
కింది ప్రశ్నలకు సరైన జవాబును గుర్తించి (A/B/C/D) సంకేతాన్ని బ్రాకెట్లలో రాయండి. (10 × 1 = 10 మా.)

ప్రశ్న 11.
వైష్ణవి చక్కగా చదువుకుంటుంది. (గీత గీసిన పదం ఏ భాషాభాగం)
A) సర్వనామము
B) నామవాచకం
C) క్రియ
D) విశేషణము
జవాబు:
B) నామవాచకం

ప్రశ్న 12.
అమీనా టీచర్ పాఠం చెబుతున్నది. (క్రియా పదాన్ని గుర్తించండి)
A) అమీనా
B) చెబుతున్నది
C) పాఠం
D) టీచర్
జవాబు:
B) చెబుతున్నది

ప్రశ్న 13.
రాజు, రాము …………. బహుమతి కొన్నాడు. (విభక్తి ప్రత్యయాన్ని గుర్తించండి.)
A) చే
B) కంటె
C) కొరకు
D) లో
జవాబు:
C) కొరకు

ప్రశ్న 14.
శివాని ………….. విహార యాత్రలు చేయాలంటే చాలా ఇష్టం. (విభక్తి ప్రత్యయాన్ని గుర్తించండి)
A) కి
B) వలన
C) ను
D) కంటె
జవాబు:
A) కి

ప్రశ్న 15.
చార్మినార్ను కులీ కుతుబ్ షా చాలా పటిష్టంగా నిర్మించాడు. (‘కర్త’ పదాన్ని గుర్తించండి)
A) చార్మినార్
B) నిర్మించాడు
C) కులీ కుతుబ్ షా
D) పటిష్టంగా
జవాబు:
C) కులీ కుతుబ్ షా

ప్రశ్న 16.
పద్మజ పుస్తకం తీసింది. పద్మజ కవితలు రాసింది. (సంక్లిష్ట వాక్యంగా మార్చండి)
A) పద్మజ పుస్తకం’ తీసినందుకు కవితలు రాసింది.
B) పద్మజ పుస్తకం తీసినందువల్ల కవితలు రాసింది.
C) పద్మజ పుస్తకం తీసి కవితలు రాసింది.
D) పద్మజ పుస్తకంలో కవితలు రాసింది.
జవాబు:
C) పద్మజ పుస్తకం తీసి కవితలు రాసింది.

ప్రశ్న 17.
రథానికి నాలుగు చక్రాలు ఉన్నాయి. (గీత గీసిన పదం ఏ సమాసం)
A) ద్వంద్వ
B) తత్పురుష
C) బహువ్రీహి
D) ద్విగు
జవాబు:
D) ద్విగు

ప్రశ్న 18.
మా నాన్న సంతలో కూరగాయలు తెచ్చాడు. (ద్వంద్వ సమాస పదాన్ని గుర్తించండి)
A) వెళ్ళి
B) కూరగాయలు
C) నాన్న
D) తెచ్చాడు
జవాబు:
B) కూరగాయలు

ప్రశ్న 19.
“ఎప్పుడెప్పుడు” పదాన్ని విడదీయండి.
A) ఎప్పుడు + ఎప్పుడు
B) ఎప్పు + డెప్పుడు
C) ఎప్పు + ఎప్పుడు
D) ఎప్పుడెప్పు + డు
జవాబు:
A) ఎప్పుడు + ఎప్పుడు

ప్రశ్న 20.
దొంగలకు + ఇత్తురో పదాన్ని కపపండి.
A) దొంగల ఇత్తురో
B) దొంగ లొత్తురో
C) దొంగలకిత్తురో
D) దొంగలకుఇత్తురో
జవాబు:
C) దొంగలకిత్తురో

AP 10th Class Social Model Paper 2024, AP SSC Social Model Paper 2024, AP SSC Social Question Paper 2024, AP SSC Social Previous Question Papers Pdf.

AP 10th Class Social Model Papers 2024-2025 – AP SSC Social Previous Question Papers Pdf

• AP 10th Class Social Model Paper 2023 (Board Model Paper)
• AP 10th Class Social Model Paper Set 1
• AP 10th Class Social Model Paper Set 2
• AP 10th Class Social Model Paper Set 3
• AP 10th Class Social Model Paper Set 4
• AP 10th Class Social Model Paper Set 5
• AP 10th Class Social Model Paper Set 6
• AP 10th Class Social Model Paper Set 7
• AP 10th Class Social Question Paper June 2023
• AP 10th Class Social Question Paper April 2023
• AP 10th Class Social Question Paper July 2022
• AP 10th Class Social Question Paper April 2022

AP 10th Class Social Model Paper 2024-25 Weightage

Section I (Objective Questions):

No. of Questions (1 – 12)	Syllabus	Marks
6	Paper I (Lessons 1 – 12)	6 × 1 = 6 Marks
6	Paper II (Lessons 13 – 22)	6 × 1 = 6 Marks
Total		12 × 1 = 12 Marks

Section II (Very Short Answer Questions):

No. of Questions (13 – 20)	Syllabus	Marks
4	Paper I (Lessons 1 – 12)	4 × 2 = 8 Marks
4	Paper II (Lessons 13 – 22)	4 × 2 = 8 Marks
Total		8 × 2 = 16 Marks

Section III (Short Answer Questions):

No. of Questions (21 – 28)	Syllabus	Marks
4	Paper I (Lessons 1 – 12)	4 × 4 = 16 Marks
4	Paper II (Lessons 13 – 22)	4 × 4 = 16 Marks
Total		8 × 4 = 32 Marks

Section IV (Essay Type Questions):

No. of Questions (29 – 33)	Syllabus	Marks
2	Paper I (Lessons 1 -12)	2 × 8 = 16 Marks
2	Paper II (Lessons 13 – 22)	2 × 8 = 16 Marks
1 (Map Pointing) (Q 33A & 33B)	Paper I & Paper II (Lessons 1 – 12 & 13 – 22)	4 + 4 = 8 Marks
Total		5 × 8 = 40 Marks

Section Wise Questions & Marks:

Section	Question Number	Marks
Section I	1 – 12	12 × 1 = 12 Marks
Section II	13 – 20	8 × 2 = 16 Marks
Section III	21 – 28	8 × 4 = 32 Marks
Section IV	29 – 33	5 × 8 = 40 Marks
Total	33 Questions	100 Marks

Weightage for Academic Standards:

Academic Standard	Weightage	Marks
I (Conceptual Understanding)	40%	40
II (Interpretation)	10%	10
III (Information Skills)	15%	15
IV (Current Issues)	10%	10
V (Mapping Skills)	15%	15
VI (Appreciation & Sensitivity)	10%	10
Total	100%	100 Marks

AP 10th Class Social Model Papers, AP SSC Social Model Papers, AP SSC Social Question Papers, AP SSC Social Previous Question Papers.

AP 10th Class Model Papers

AP 10th Class Physical Science Model Paper 2024, AP SSC Physical Science Model Paper 2024, AP SSC Physical Science Question Paper 2024, AP SSC Physical Science Previous Question Papers Pdf.

AP 10th Class Physical Science Model Papers 2024-2025 – AP SSC Physical Science Previous Question Papers Pdf

• AP 10th Class Physical Science Model Paper 2024 (Board Model Paper)
• AP 10th Class Physical Science Model Paper Set 1
• AP 10th Class Physical Science Model Paper Set 2
• AP 10th Class Physical Science Model Paper Set 3
• AP 10th Class Physical Science Model Paper Set 4
• AP 10th Class Physical Science Model Paper Set 5
• AP 10th Class Physical Science Model Paper Set 6
• AP 10th Class Physical Science Model Paper Set 7
• AP 10th Class Physical Science Question Paper June 2023
• AP 10th Class Physical Science Question Paper April 2023
• AP 10th Class Physical Science Question Paper June 2022
• AP 10th Class Physical Science Question Paper April 2022

AP 10th Class Physical Science Model Paper 2023-24 Weightage

		AS – I	AS – II	AS – III	AS – IV	AS – V	AS – VI	Total Questions	Total Marks
Section-I (1 Mark Questions)	PS	2	1	–	3	1	1	8	8	8
Section-II (2 Mark Questions)	PS	1	2	–	–	–	–	3	6	6
Section-III (4 Mark Questions)	PS	–	–	–	1	1	1	3	12	12
Section-IV (8 Mark Questions) (Internal Choice)	PS	2	–	1	–	–	–	3	24	24
								17Q	50	50

AP 10th Class Physical Science Model Papers, AP SSC Physical Science Model Papers, AP SSC Physical Science Question Papers, AP SSC Physical Science Previous Question Papers.

AP 10th Class Model Papers

AP 10th Class Biology Model Paper 2024, AP SSC Biology Model Paper 2024, AP SSC Biology Question Paper 2024, AP SSC Biology Previous Question Papers Pdf.

AP 10th Class Biology Model Papers 2024-2025 – AP SSC Biology Previous Question Papers Pdf

• AP 10th Class Biology Model Paper 2024 (Board Model Paper)
• AP 10th Class Biology Model Paper Set 1
• AP 10th Class Biology Model Paper Set 2
• AP 10th Class Biology Model Paper Set 3
• AP 10th Class Biology Model Paper Set 4
• AP 10th Class Biology Model Paper Set 5
• AP 10th Class Biology Model Paper Set 6
• AP 10th Class Biology Model Paper Set 7
• AP 10th Class Biology Model Paper Set 8
• AP 10th Class Biology Question Paper June 2023
• AP 10th Class Biology Question Paper April 2023
• AP 10th Class Biology Question Paper April 2022

AP 10th Class Biology Model Paper 2024-25 Weightage

	AS1 (6Q)	AS2 (3Q)	AS3 (1Q)	AS4 (3Q)	AS5 (2Q)	AS6 (2Q)	Total (17Q)
1M	2	1		1	1	1	6M
2M	1	2		1			8M
4M	2			1	1 + 1	1	20M
8M	1 + 1		1 + 1				16M (2 Internal Choice)
	20M	5M	8M	7M	5M	5M	50M
1 + 1 means internal choice

AP 10th Class Biology Model Papers, AP SSC Biology Model Papers, AP SSC Biology Question Papers, AP SSC Biology Previous Question Papers.

AP 10th Class Model Papers

AP 10th Class English Model Paper 2024, AP SSC English Model Paper 2024, AP SSC English Question Paper 2024, AP SSC English Previous Question Papers Pdf.

AP 10th Class English Model Papers 2024-2025 – AP SSC English Previous Question Papers Pdf

• AP 10th Class English Model Paper 2023 (Board Model Paper)
• AP 10th Class English Model Paper Set 1
• AP 10th Class English Model Paper Set 2
• AP 10th Class English Model Paper Set 3
• AP 10th Class English Model Paper Set 4
• AP 10th Class English Model Paper Set 5
• AP 10th Class English Model Paper Set 6
• AP 10th Class English Model Paper Set 7
• AP 10th Class English Question Paper June 2023
• AP 10th Class English Question Paper April 2023
• AP 10th Class English Question Paper June 2022
• AP 10th Class English Question Paper April 2022

AP 10th Class English Model Paper 2024-25 Weightage

Section – A
Reading Comprehension (30 Marks)

Questions 1 to 5 – From A – Reading (2 Wh Questions + 3 MCQs) (5 × 2 = 10 Marks)

Questions 6 to 8 – From B – Reading (Poem/Prose) (3 MCQs) (3 × 2 = 6 Marks)

Questions 9 to 10 – From C – Reading (2 MCQs) (2 × 2 = 4 Marks)

Questions 11 to 15 – Study Skills (2 Wh Qns + 3 MCQs) (5 × 2 = 10 Marks)

Section – B
Vocabulary & Grammar (40 Marks)

Question 16 – Combine the sentences using Relative clause/Nonfinite clauses (Ref: Units – 1 & 5) (2 Marks)

Question 17 – Change the Voice (2 Marks)

Question 18 – Combine the sentences using the linkers given in the brackets. (Ref: Units – 3, Page 92 & Unit 6 Page 192) (2 Marks)

Question 19 – Fill in the blanks with compound Prepositional phrases and Prepositions given in brackets. (Ref: Unit – 2 & Unit 4) (2 × 1 = 2 Marks)

Question 20 – Fill in the blanks with the correct form of verbs (Ref: Units 2, 3 & 4) (2 × 1 = 2 Marks)

Question 21 – Give a suitable Advice (2 Marks)

Question 22 – Change into a Polite Request (2 Marks)

Question 23 – Identify the Expression (2 × 1 = 2 Marks)

Question 24 – Pick out the right synonyms for the underlined words (A – Readings) (4 × 1 = 4 Marks)

Question 25 – Choose the correct antonyms for the underlined words (A – Readings) (4 × 1 = 4 Marks)

Question 26 – Choose the right forms of words (A – Readings) (4 × 1 = 4 Marks)

Question 27 – Fill in the blanks with ‘ae’, ‘au’, ‘ie’, ‘ei’, ‘ou’, ‘oo’ or ‘ee’ (A – Readings) (2 × 1 = 2 Marks)

Question 28 – Fill in the blanks with suitable suffixes (A – Readings) (2 × 1 = 2 Marks)

Question 29 – Find the wrongly spelled word and write the correct answer. (A – Readings) (2 × 1 = 2 Marks)

Question 30 – Dictionary Skills (2 × 1 = 2 Marks)

Question 31 – Write under correct headings (Ref: Units 1, 2, 3 & 4) (8 × ¼ = 2 Marks)

Question 32 – Match the one-word substitutes with the right phrases (Ref: Units 1, 4 & 5) (4 × ½ = 2 Marks)

Section – C
Creative Expression (30 Marks)

Question 33 – (a) Conversation (A, B, C Readings) (OR) (b) Diary Entry (10 Marks)

Question 34 – (a) Letter Writing (OR) (b) Biographical Sketch (10 Marks)

Question 35 – (a) Framing ‘WH’ Questions (Ref: C – Reading) (OR) (b) Information Transfer (10 Marks)

AP 10th Class English Model Papers, AP SSC English Model Papers, AP SSC English Question Papers, AP SSC English Previous Question Papers.

AP 10th Class Model Papers

AP 10th Class Hindi Model Paper 2024, AP SSC Hindi Model Paper 2024, AP SSC Hindi Question Paper 2024, AP SSC Hindi Previous Question Papers Pdf.

AP 10th Class Hindi Model Papers 2024-2025 – AP SSC Hindi Previous Question Papers Pdf

• AP 10th Class Hindi Model Paper 2024 (Board Model Paper)
• AP 10th Class Hindi Model Paper 2023 (Board Model Paper)
• AP 10th Class Hindi Model Paper Set 1
• AP 10th Class Hindi Model Paper Set 2
• AP 10th Class Hindi Model Paper Set 3
• AP 10th Class Hindi Model Paper Set 4
• AP 10th Class Hindi Model Paper Set 5
• AP 10th Class Hindi Model Paper Set 6
• AP 10th Class Hindi Question Paper June 2023
• AP 10th Class Hindi Question Paper April 2023
• AP 10th Class Hindi Question Paper June 2022
• AP 10th Class Hindi Question Paper April 2022

AP 10th Class Hindi Model Paper 2023-24 Weightage

प्रश्न संख्या	प्रश्नवार विश्लेषण	प्रश्नों की संख्या	अंक	कुल अंक
भाग- I (भाषा की बात)
1	तत्सम तद्भव (दिए गए वाक्य में से तत्सम के लिए तद्भव या तद्भव के लिए तत्सम शब्द पहचानकर लिखना होगा।)	1Q	1M	1M
2	क्रिया विशेषण (एक शब्द में उत्तर लिखना होगा।)	1Q	1M	1M
3	अक्षरों को अंकों में लिखना होगा।	1Q	1M	1M
4	कारक चिह्न – (विकल्पों में से सही कारक चिह्न पहचानकर लिखेना होगा।)	1Q	1M	1M
5	समास – (निर्देश के अनुसार विकल्पों में से चुन कर लिखना होगा।)	1Q	1M	1M
6	संधि विच्छेद – (निर्देश के अनुसार लिखना होगा।)	1Q	1M	1M
7	निम्न लिखित शब्द का सही अर्थ विकल्पों में से पहचान कर लिखना होगा।	1Q	1M	1M
8	मुहावरा – (मुहावरेदार शब्द को विकल्पों में से पहचान कर लिखना होगा।)	1Q	1M	1M
9	लिंग (सूचना के अनुसार लिंग बदलकर लिखना होगा।)	1Q	1M	1M
10	वचन (सूचना के अनुसार वचन बदलकर लिखना होगा।)	1Q	1M	1M
11	काल (निर्देश के अनुसार बदलना होगा।)	1Q	1M	1M
12	शुद्धरूप (निर्देश के अनुसार लिखना होगा।)	1Q	1M	1M
भाग- II (अर्थग्राह्यता)
13	पठित गद्य पाठों में से एक अनुच्छेद दिया जाएगा। उस में से उपसर्ग, प्रत्यय, पर्याय, विलोम, संज्ञा, सर्वनाम, विशेषण, क्रियाओं में से कोई 5 व्याकरणिक अंश देकर पहचानने को कहेंगे। अ, आ, इ, ई और उ के प्रश्न होंगे।	5Q	1M	5M
14	पठित पद्य पाठों में से एक पद्यांश दिया जाएगा। अ, आ, इ, ई और उ के प्रश्न होंगे। (ये बहु विकल्पीय प्रश्न होंगे।)	5Q	1M	5M
15	पठित गद्य पाठों में से एक गद्यांश दिया जाएगा। अ, आ, इ, ई और उ के प्रश्न होंगे। एक वाक्य में उत्तर देना होगा।	5Q	1M	5M
16	पठित गद्य पाठों में से एक गद्यांश दिया जाएगा। अ, आ, इ, ई और उ के प्रश्न होंगे। (ये बहुविकल्पीय प्रश्न होंगे।)	5Q	1M	5M
भाग – III (अभिव्यक्ति)
17	पाठ्य पुस्तक में दिए गए कवि परिचयों से संबंधित प्रश्नों की सही जोड़ी बनाना होगा।	1Q	4M	4M
18	लेखक का परिचय पढ़कर रिक्त स्थानों की पूर्ती करना होगा।	1Q	4M	4M
भाग – IV (अभिव्यक्ति)
19, 20	पद्य भाग से दो प्रश्न दिये जायेंगे। तीन-चार वाक्यों में उत्तर देना होगा।	2Q	3M	6M
21, 22, 23	गद्य भाग से तीन प्रश्न दिये जायेंगे। तीन-चार वाक्यों में उत्तर देना होगा।	3Q	3M	9M
24, 25, 26	उपवाचक से तीन प्रश्न दिये जायेंगे। तीन-चार वाक्यों में उत्तर देना होगा।	3Q	3M	9M
भाग – V (अभिव्यक्ति)
27 (अ, आ)	पद्य भाग से दो सारांशात्मक प्रश्न पूछे जायेंगे। किसी एक प्रश्न का उत्तर 10 पंक्तियों में देना होगा। (अ और आ) के प्रश्न होंगे।	1Q	10M	10M
28 (अ, आ)	गद्य भाग से दो सारांशात्मक प्रश्न पूछे जायेंगे। किसी एक प्रश्न का उत्तर 10 पंक्तियों में देना होगा। (अ और आ) के प्रश्न होंगे।	1Q	10M	10M
भाग – VI (सृजनात्मक अभिव्यक्ति)
29 (अ, आ)	एक औपचारिक और एक अनौपचारिक पत्र दिये जायेंगे। किसी एक प्रश्न का उत्तर देना होगा। (अ और आ) के प्रश्न होंगे।	1Q	8M	8M
30 (अ, आ)	दो निबंध दिए जायेंगे। उनमें से एक निबंध को चुनकर उचित शब्दों से रिक्त स्थानों की पूर्ती करना होगा।	1Q	8M	8M

शैक्षिक मापदंड – भार तालिका

शैक्षिक मापदंड	कुल अंक	प्रतिशत
1. अर्थग्राह्यता	15M	15%
2. अभिव्यक्ति	52M	52%
3. भाषा की बात	17M	17%
4. सृजनात्मकता	16M	16%
कुल	100M	100%

प्रश्नों के स्वरूप के अनुसार भार तालिका

प्रश्न का स्वरूप	प्रस्नों की संख्या	कुल अंक
1. निबंधात्मक प्रश्न	3	28
2. लघु उत्तरात्मक प्रश्न	8	24
3. अति लघु उत्तरात्मक प्रश्न	4	20
4. लक्ष्यात्मक प्रश्न	15	28
कुल	30	100

पाठ्य विषयों के आधार पर भार तालिका

	लक्ष्यात्मक प्रश्न	लघु उत्तरात्मक प्रश्न	अति लघु उत्तरात्मक प्रश्न	निबंधात्मक प्रश्न	कुल अंक
1. पद्य भाग	5(1), 1(4)	2(6)	1(5)	1(10)	30
2. गद्य भाग	7(1), 1(4)	3(9)	3(15)	1(10)	45
3. उपवाचक	–	–	3(3)	–	9
4. सृजनात्मकता	1(8)	–	–	1(8)	16
कुल	13	6	8	3	100

AP 10th Class Hindi Model Papers, AP SSC Hindi Model Papers, AP SSC Hindi Question Papers, AP SSC Hindi Previous Question Papers.

AP 10th Class Model Papers

AP 10th Class Telugu Model Paper 2024, AP SSC Telugu Model Paper 2024, AP SSC Telugu Question Paper 2024, AP SSC Telugu Previous Question Papers Pdf.

AP 10th Class Telugu Model Papers 2024-2025 – AP SSC Telugu Previous Question Papers Pdf

• AP 10th Class Telugu Model Paper 2024 (Board Model Paper)
• AP 10th Class Telugu Model Paper Set 1
• AP 10th Class Telugu Model Paper Set 2
• AP 10th Class Telugu Model Paper Set 3
• AP 10th Class Telugu Model Paper Set 4
• AP 10th Class Telugu Model Paper Set 5
• AP 10th Class Telugu Model Paper Set 6
• AP 10th Class Telugu Model Paper Set 7
• AP 10th Class Telugu Model Paper Set 8
• AP 10th Class Telugu Model Paper Set 9
• AP 10th Class Telugu Question Paper June 2023
• AP 10th Class Telugu Question Paper April 2023

AP 10th Class Telugu Model Paper 2024-25 Weightage

I. విద్యా ప్రమాణాలు – భారత్వ పట్టిక

విద్యా ప్రమాణాలు	మార్కులు	శాతం
1. అవగాహన – ప్రతిస్పందన	32	32%
2. వ్యక్తీకరణ – సృజనాత్మకత	36	36%
3. భాషాంశాలు	32	32%
మొత్తం	100	100%

II. పాఠ్యభారత్వ పట్టిక / విషయరూప భారత్వ పట్టిక

పాఠ్యాంశాలు / విషయం	మార్కులు	శాతం
1. పద్యం	20	20%
2. గద్యం (పరిచిత, అపరిచిత గద్యాలతో కలిపి)	20	20%
3. ఉపవాచకం	20	20%
4. పద్యం / గద్యం నుండి సృజనాత్మక ప్రశ్న	8	8%
5. భాషాంశాలు	32	32%
మొత్తం	100	100%

III. ప్రశ్నానురూప భారత్వ పట్టిక

ప్రశ్న స్వరూపం	ప్రశ్నల సంఖ్య	మార్కులు	మొత్తం మార్కులు	శాతం
1. వ్యాసరూప ప్రశ్నలు	7	8	56	56%
2. లఘు ప్రశ్నలు	3	4	12	12%
3. అతిలఘు ప్రశ్నలు	9	2	18	18%
4. లక్ష్యాత్మక ప్రశ్నలు	14	1	14	14%
మొత్తం	33		100	100%

AP 10th Class Telugu Model Papers, AP SSC Telugu Model Papers, AP SSC Telugu Question Papers, AP SSC Telugu Previous Question Papers.

AP 10th Class Model Papers

AP 10th Class Maths Model Paper 2024, AP SSC Maths Model Paper 2024, AP SSC Maths Question Paper 2024, AP SSC Maths Previous Question Papers Pdf.

AP 10th Class Maths Model Papers 2024-2025 – AP SSC Maths Previous Question Papers Pdf

• AP 10th Class Maths Model Paper 2023 (Board Model Paper)
• AP 10th Class Maths Model Paper Set 1
• AP 10th Class Maths Model Paper Set 2
• AP 10th Class Maths Model Paper Set 3
• AP 10th Class Maths Model Paper Set 4
• AP 10th Class Maths Model Paper Set 5
• AP 10th Class Maths Model Paper Set 6
• AP 10th Class Maths Model Paper Set 7
• AP 10th Class Maths Question Paper June 2023
• AP 10th Class Maths Question Paper April 2023
• AP 10th Class Maths Question Paper July 2022
• AP 10th Class Maths Question Paper April 2022

AP 10th Class Maths Model Paper 2024-25 Weightage:

Academic Standard – I	Academic Standard –II	Academic Standard – III	Academic Standard – IV	Academic Standard – V
6 × 1 Marks = 6 Marks	2 × 1 Marks = 2 Marks	2 × 1 Marks = 2 Marks	1 × 1 Marks = 1 Marks	1 × 1 Marks = 1 Marks
3 × 2 Marks = 6 Marks	1 × 2 Marks = 2 Marks	2 × 2 Marks = 4 Marks	1 × 2 Marks = 2 Marks	1 × 2 Marks = 2 Marks
3 × 4 Marks = 12 Marks	2 × 4 Marks = 8 Marks	1 × 4 Marks = 4 Marks	1 × 4 Marks = 4 Marks	1 × 4 Marks = 4 Marks
2 × 8 Marks = 16 Marks	1 × 8 Marks = 8 Marks	–	1 × 8 Marks = 8 Marks	1 × 8 Marks = 8 Marks
40 Marks	20 Marks	10 Marks	15 Marks	15 Marks

AP 10th Class Maths Model Papers, AP SSC Maths Model Papers, AP SSC Maths Question Papers, AP SSC Maths Previous Question Papers.

AP 10th Class Model Papers

The strategic use of TS 10th Class Maths Model Papers and TS 10th Class Maths Question Paper April 2023 can significantly enhance a student’s problem-solving skills.

TS 10th Class Maths Question Paper April 2023

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. Answer all the questions under Part – A on a separate answer book.
2. Write the answers to the questions under Part – B on the question paper itself and attach it to the answer book of Part – A.

Part – A (60 Marks)
Section – I (6 × 2 = 12 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 1.
Find the centroid of the triangle whose vertices are (2, 3) (-4, 7) and (2, -4).
Answer:

Question 2.
Find the probability of getting a ‘vowel’ if a letter is chosen randomly from the word “INNOVATION’.
Answer:
P(E) = \(\frac{\text { Number of favourble outcomes }}{\text { Number of total outcomes }}\)
Favourable outcomes = i, o, a, i, o
Number of favourable outcomes = 5.
Number of total outcomes = 10
P(getting a vowel) = \(\frac{5}{10}\) = \(\frac{1}{2}\)

Question 3.
Express ‘tan θ’ in terms of ‘sin θ’.
Answer:
‘tan θ’ = \(\frac{\sin \theta}{\cos \theta}\)
sin² θ + cos² θ = 1
cos θ = 1 – sin² θ
cos² θ = \(\sqrt{1-\sin ^2 \theta}\)
∴ tan θ = \(\sqrt{\frac{\sin \theta}{1-\sin ^2 \theta}}\)

Question 4.
“An observer standing at a distance of 10m from the foot of a tower, observes its top with an angle of elevation of 60°.” Draw a suitable diagram for this situation.
Answer:
AB – Tower
C – Position of observer
60° – Angle of elevation

Question 5.
The sides of a triangle measure 2√2, 4 and 2 √6 units. Is it a right-angled triangle ? Justify.
Answer:
(2√2)² = 8
(4)² = 16
(2√6)² = 24, (2√2)² + (4)² = (2√6)²
∴ If sum of squares of two sides of a triangel is equal to the square of the third side, then the triangle is a right angled triangle. (Converse of Pytha groups theorem)
∴ Given triangle is a right – angled triangle.

Question 6.
Solve the quadratic equation 2 sin² θ – 3 sin θ + 1 = 0, where 0° < θ ≤ 90°.
Answer:
2 sin² θ – 3 sin θ + 1 = θ
where 0° < θ ≤ 90°
2 sin² θ – 2 sin θ – sin θ + 1 = θ
2 sin θ (sin θ – 1) – 1 (sinθ – 1) = 0
(2 sin θ – 1) (sin θ – 1) = 0

2 sin θ – 1 = 0
2 sin θ = 1
sin θ = \(\frac{1}{2}\)
sin θ = \(\frac{1}{2}\) = sin 30°
θ = 30°

sin θ – 1 = 0
sin θ = 1
sin θ = 1 = sin 90°
θ = 90°

Section – II (6 × 4 = 24 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 7.
Write the formula for Median of a grouped data and explain each term of it.
Answer:
Median = l + \(\left[\frac{\frac{n}{2}-c f}{f}\right]\) × h
l = lower boundary of median class.
n = number of observations.
cf = cumulative frequency of class preceding the median class.
f = frequency of median class.
h – class size.

Question 8.
If x² + y² = 10xy, then prove that 2 log (x + y) = logx + logy + 2 log 2 + log3.
Answer:
Given equation x² + y² = 10xy
Adding 2xy on both sides
x² + y² + 2xy = 10xy + 2xy
(x + y)² = 12xy
Applying log on both sides
log (x + y)² = log (12xy)
2 log (x + y) = log 12 + log x + log y
∴ 2 log (x +y) = log 4 + log 3 + log x + log y
Hence proved.

Question 9.
A strip of width 4 cm is attached to one side of a square to form a rectangle. The area of the rectangle formed is 77 cm², then find the length of the side of the square.

Answer:
Let the side of the square be ‘x’ cm.
Then length of rectangle = x + 4 cm
Breadth of rectangle = x = cm

Area of rectangle = length × breadth
= (x + 4) x

Question 10.
From the given Venn diagram šhow that n (A∪B) = n (A) + n (B) – n (A∩B).

Answer:
A – { b, d, m, a, e, u},
B = {a, e, u, p, q, r, t}
(A∪B) = {b, d, m, a, e, u, p, q, r, t}
(A∩B) = {a, e, u}
n (A) = 6, n (B) = 7
n (A ∪ B) = 10, n (A∩B) = 3
LHS n (A ∪ B) = 10
RHS n (a) + n (B) – n(A∩B)
= 6 + 7-3 = 13-3 = 10 LHS = RHS
∴ n (A∪B) = n (A) + n(B) – n (A∩B)

Question 11.
A box contains four slips numbered 1, 2, 3, 4 and another box contains five slips numbered 5, 6, 7, 8, 9. If one slip is taken randomly from each box,
i) How many number pairs are possible ? ,
ii) What is the probability of both being odd ? „
iii) What is the probability of getting the sum of the numbers 10 ?
Answer:
i) Possible number pairs
(1, 5) (1, 6) (1, 7) (1, 8) (1, 9)
(2, 5) (2, 6) (2, 7) (2, 8) (2, 9)
(3, 5) (3, 6) (3, 7) (3, 8) (3, 9)
(4, 5) (4, 6) (4, 7) (4, 8) (4, 9)
Number of possible number pairs = 20

ii) Favourable outcomes (1, 5), (1,7), (1, 9), (3, 5), (3,7), (3, 9)
Number of favourable outcomes = 6
P (getting both being odd)
= \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}\)
= \(\frac{6}{20}\) = \(\frac{3}{10}\)

iii) Favourable outcomes (1, 9), (2, 8) (3, 7), (4, 6)
Number of favourable outcomes = 4
P (getting the sum of the numbers 10)
= \(\frac{4}{20}\) = \(\frac{1}{5}\)

Question 12.
Which term of the A.P. 21, 18, 15, ………………. is – 81 ? Also find the term which becomes zero.
Answer:
Arithmetic progression 21, 18, 15, ……..
a = 21; d = 18 – 21 = -3; a_n = -81
n = ?
a_n = a + (n – 1) d
– 81 = 21 + (n – 1) (- 3)
(n – 1) (- 3) = – 81 – 21 = – 102
n – 1 = \(\frac{-102}{-3}\) = 34
n = 34 + 1 = 35
-81 is 35^th term of that A.P.
again a_n = 0; n = ?
⇒ a_n = a + (n – 1) d
0 = 21 + (n – 1) (- 3)
(n – 1) (- 3) = – 21
n- 1 = \(\frac{-21}{-3}\) = 7
n – 1 = 7 ⇒ n = 7 + 1 = 8
∴ 8^th term of that A.P. is zero.

Section – III (4 × 6 = 24 Marks)

Note :

1. Answer any 4 questions from the given six questions.
2. Each question carries 6 marks.

Question 13.
Draw the graph of the quadratic polynomial p(x) = x² – 4x + 3 and find the zeroes of the polynomial from the graph.
Answer:
y = p(x) = x² – 4x + 3

Question 14.
In an acute angled triangle ABC, if sin (A + B – C) = \(\frac{I}{2}\) and cos (B + C – A) = \(\frac{I}{2}\), then find ∠A, ∠B and ∠C.
Answer:
sin (A + B – C) = \(\frac{I}{2}\) = sin 30°
⇒ A + B – C = 30° ………….. (1)
cos (B + C – A) = \(\frac{I}{2}\) = cos 60°
⇒ B + C – A = 60° ……………. (2)
On adding equations (1) and (2)

⇒ B = \(\frac{90}{2}\) = 45°
Substituting the value of B in equation (2)
C – 4 = 60° – 45° = 15° ………………. (3)
B + C + A = 180°
(sum of angles of a triangle)
C + A = 180° – 45° = 135° …………….. (4)
Now solving equations (3) and (4)

∠A = 135° – 75° = 60°
∠A = 60°, = 45°, ∠C =75°

Question 15.
Find the mode for the following data.

Answer:

since the maximum families 40 lies in the class 1500 – 2000, this is the required modal class.
Lower boundary of the modal class (l) = 1500
Frequency of the modal class (f₁) = 40
Frequency of the class preceding the modal class f₀ = 24
Frequency of the class succeeding the modal class f₂ = 33
Height of the class, h = 500
Model (Z) = l + \(\frac{\left[\mathrm{f}_1-\mathrm{f}_0\right]}{2 \times \mathrm{f}_1-\left[\mathrm{f}_0+\mathrm{f}_2\right]}\) × h = 1500 + \(\frac{40-24}{2 \times 40-(24+33)}\) × 500
= 1500 + \(\frac{16 \times 500}{80-57}\) = 500 + \(\frac{8000}{23}\) = 1500 + 347.826 = ₹ 1847.83
Hence, modal monthly income = ₹ 1847.83
Assumed mean (a) = 3250
Σf_i = 200; Σu_if_i = – 235
Mean monthly income= \(\bar{x}\) = a + \(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\) × h = 3250 – \(\frac{235}{200}\) × 500

Question 16.
If A (-2, 2), B (a, 6), C (4, b) and D (2, -2) are the vertices of a parallelogram ABCD, then find the values of a and b. Also find the lengths of its sides.
Answer:

Vertices of parallelogram ABCD are
A (-2, 2), B (a, 6), C (4, b), D (2, -2)
Mid point of AC = (\(\frac{-2+4}{2}, \frac{2+b}{2}\)) = (1, \(\frac{2+b}{2}\))
Mid point of BD = (\(\frac{a+2}{2}, \frac{6-2}{2}\)) = (\(\frac{a+2}{2}\), 2)
Since it is a parallelogram, mid-points of diagonals coincide.
So, (1, \(\frac{2+b}{2}\)) = (\(\frac{a+2}{2}\), 2)
\(\frac{1}{1}\) = \(\frac{a+2}{2}\)
a + 2 = 2
a = 2 – 2 = 0

\(\frac{2+b}{2}\) = \(\frac{2}{1}\)
2 + b = 4
b = 4 – 2 = 2

Question 17.
Construct triangle ABC with BC = 7 cm, ∠B = 45° and ∠C = 60°. Then construct another triangle similar to Δ ABC, whose sides are \(\frac{3}{5}\) times of the corresponding sides of Δ ABC.
Answer:

Construction:
Steps of Construction:

1. Construct Δ ABC with given measurements.
2. Draw \(\overrightarrow{\mathrm{BX}}\) such that ∠CBX is an acute angle.
3. Locate points P₁, P₂, P₃, P₄, P₅ on \(\overrightarrow{\mathrm{BX}}\) such that
   BP₁ = P₁P₂ = P₂P₃ = P₃P₄ = P₄P₅
4. Joint P₅ and C.
5. Draw a parallel line to P₅ C through P₃to meet BC at C¹.
6. Draw a parallel line to AC through C¹ to meet BA at A¹.
7. Δ A¹ BC¹ is required similar triangle.

Question 18.
Prove that 2√3 + √5 is an irrational number.
Answer:
To Prove: 2√3 + √5 is an irrational number. On contrary, let us suppose that 2√3 + √5 be a rational number. ”
Then 2√3 +√5 = \(\frac{\mathrm{p}}{\mathrm{q}}\)
squaring on both sides, we get (2√3 + √5)² = (\(\frac{\mathrm{p}}{\mathrm{q}}\))²
(2√3)² + (√5)² + 2 (2√3) (√5) = \(\frac{p^2}{q^2}\)
12 + 5+ 4\(\sqrt{15}\) = \(\frac{p^2}{q^2}\)
17 + 4\(\sqrt{15}\) = \(\frac{p^2}{q^2}\) ⇒ 4\(\sqrt{15}\) = \(\frac{p^2}{q^2}\) – 17 ⇒ \(\sqrt{15}\) = \(\frac{p^2-17 q^2}{4 q^2}\)
L H. S = an irrational number.
R. H. S = p, q being integers, \(\frac{p^2-17 q^2}{4 q^2}\)
is a rational number.

This is a contradiction to the fact that \(\overline{\mathrm{X}}\) is an irrational. This is due to our assumption that 2√3 + √5 is rational. Hence our assumption is wrong, and 2√3 + √5 is an irrational number.

Also;
(2√3 + √5) (2√3 – √5) = (2√3)² – (√5)²
[∵ (a + b) (a – b) = a² – b²] = 4 × 3 – 5 = 12 – 5 = 7, a rational number.

Part – B (20 Marks)

Note :

1. All questions are to be answered.
2. Each question carries 1 mark.
3. Answers are to be written in the Question paper only.
4. Marks will not be given for overwriting, rewriting or erased answers.

I. Write the CAPITAL LETTERS (A, B, C, D) of the correct answer in the brackets provided against each question, 20 × 1 = 20 M

Question 1.
Prime factorization of 98 is ……………. .
A) 2² × 7
B) 2² × 7²
C) 2 × 7²
D) 2³ × 7
Answer:
C) 2 × 7²

Question 2.
The 30^th term of the A.P. 10, 7, 4, ……………. is ……………….. .
A) 87
B) 77
C) -77
D) -87
Answer:
C) -77

Question 3.
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is ……………….. .
A) 5
B) 12
C) 11
D) 7 + √5
Answer:
B) 12

Question 4.
If x⁴ + 3x² + 7 is divided by x + 3, then the possible degrees of quotient and remainder are …………… .
A) 3, 0
B) 4, 1
C) 3, 1
D) 4, 0
Answer:
A) 3, 0

Question 5.
The pair of equations 9x + 3y +12 = 0 and 18x + 6y + 26 = 0 has …………… .
A) unique solution.
B) two solutions.
C) infinitely many solutions.
D) no solution.
Answer:
D) no solution.

Question 6.
“The product of two consecutive positive integers is 30”. This can be expressed algebraically as …………….. .
A) x(x + 2) = 30
B) x(x – 2) = 30
C) x(x – 3) = 30
D) x(x + 1) = 30
Answer:
D) x(x + 1) = 30

Question 7.
A cylindrical pencil sharpened at one end is a combination of ……………….. .
A) a cone and a cylinder.
B) a cone and a hemisphere.
C) a hemisphere and a cylinder.
D) two cylinders.
Answer:
A) a cone and a cylinder.

Question 8.
If a solid sphere is melted and converted into a solid cylinder, then the volume of the cylinder will ……………….. .
A) become double.
B) remains unchanged.
C) increase.
D) decrease.
Answer:
B) remains unchanged.

Question 9.
If Δ ABC is right-angled at C, then the value of cos (A + B) is ………………… .
A) 0
B) \(\frac{I}{2}\)
C) \(\frac{\sqrt{3}}{2}\)
D) 1
Answer:
A) 0

Question 10.
If the mean of a, a + 3, a + 6, a + 9 and a + 12 is 10, then the value of ‘a’ is …………………. .
A) 1
B) 2
C) 3
D) 4
Answer:
D) 4

Question 11.
A fish tank has 5 male fish and 8 female fish. If a fish is randomly taken out of it, then the probability of getting a male fish is ……………….. .
A) \(\frac{5}{8}\)
B) \(\frac{5}{13}\)
C) \(\frac{8}{5}\)
D) \(\frac{13}{5}\)
Answer:
B) \(\frac{5}{13}\)

Question 12.
The roster form of the set A = {x: x = n², n ∈ N, n < 5} is ………………….. .
A) A = {1, 4, 9, 16, 25}
B) A = {0, 1, 4, 9, 16}
C) A = {1, 4, 9, 16 }
D) A = {0, 1, 4, 9, 16, 25}
Answer:
C) A = {1, 4, 9, 16 }

Question 13.
If the zeroes of the polynomial x² + (a + 1) x + b are 2 and -3, then the values of a and b are ………………. .
A) a = -5, b = -1
B) a = 5, b = -1
C) a = -2, b = 6
D) a = 0,b = -6
Answer:
D) a = 0,b = -6

Question 14.
Among the following, the pair of triangles which are always similar is ……………… .
A) two isosceles triangles.
B) two scalene triangles.
C) two equilateral triangles.
D) two right-angled triangles.
Answer:
C) two equilateral triangles.

Question 15.
Corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm², then the area of the larger triangle is ……………… .
A) 108 cm²
B) 72 cm²
C) 36 cm²
D) 90 cm²
Answer:
A) 108 cm²

Question 16.
If the length of a tangent from an external point ‘A’ at a distance of 5 cm from the centre of the circle is 4 cm, then the radius, of the circle is ……………….. .
A) 5 cm
B) 3 cm
C) 7 cm
D) 5 + √3 cm
Answer:
B) 3 cm

Question 17.
The quadratic equation with roots 2 + √3 and 2 – √3 is ………………….. .
A) x² + 4x + 1 = 0
B) x² + 4x – 1 = 0
C) x² – 4x + 1 = 0
D) x² – 4x – 1 =0
Answer:
C) x² – 4x + 1 = 0

Question 18.
The LCM of the given numbers x and y where y is a multiple of x is …………………….. .
A) x
B) y
C) x^y
D) x + y
Answer:
B) y

Question 19.
The value of (sin 30° + cos 60°) – (sin 60° + cos 30°) is ………………… .
A) 0
B) 1 + 2√3
C) 1 – √3
D) 1 + √3
Answer:
C) 1 – √3

Question 20.
In a random experiment E and E are complementary events. If P (E) = 0.43, then P(\(\overline{\mathbf{E}}\)) is ……………….. .
A) 0.57
B) 0.43
C) 0.17
D) 1
Answer:
A) 0.57

AP 10th Class Model Paper 2024 Pdf: AP SSC Model Papers 2024 Pdf English Medium, AP SSC Question Paper 2024 Pdf Download, AP SSC Previous Question Papers Pdf, AP 10th Class Public Exam Model Paper 2024, AP SSC 10th Previous Year Question Papers, AP 10th Class Model Papers 2024, SCERT Model Question Papers For Class 10 in AP.

AP 10th Class Public Exam Model Paper 2024 – AP SSC Previous Question Papers English & Telugu Medium

• AP 10th Class Maths Model Papers
• AP 10th Class Biology Model Papers
• AP 10th Class Physical Science Model Papers
• AP 10th Class Social Model Papers
• AP 10th Class Telugu Model Papers
• AP 10th Class English Model Papers
• AP 10th Class Hindi Model Papers

AP Board SSC PUBLIC EXAMINATIONS – 2024
SUBJECT WISE MODEL QUESTION PAPERS & BLUE PRINTS & WEIGHTAGE

S.No	SUBJECTS	PAPER CODES	DOWNLOAD
1	1ST LANGUAGE (TELUGU)	01T & 02T	CLICK HERE
2	1ST LANGUAGE (HINDI)	01H & 02H	CLICK HERE
3	1ST LANGUAGE (TAMIL)	01A & 02A	CLICK HERE
4	1ST LANGUAGE (KANNADA)	01K & 02K	CLICK HERE
5	1ST LANGUAGE (ODIA)	01 ‘O’ & 02’O’	CLICK HERE
6	1ST LANGUAGE (URDU)	01U & 02U	CLICK HERE
7	1ST LANGUAGE PAPER – I (COMPOSITE TELUGU)	03T	CLICK HERE
8	1ST LANGUAGE PAPER – II (COMPOSITE SANSKRIT)	04S	CLICK HERE
9	2ND LANGUAGE ( TELUGU)	09T	CLICK HERE
10	2ND LANGUAGE ( HINDI)	09H	CLICK HERE
11	3RD LANGUAGE ( ENGLISH)	13E & 14E	CLICK HERE
12	MATHEMATICS (ENGLISH – MEDIUM)	15E & 16E	CLICK HERE
13	MATHEMATICS (TELUGU – MEDIUM)	15T & 16E	CLICK HERE
14	GENERAL SCIENCE – PAPER-I (ENGLISH – MEDIUM)	19E	CLICK HERE
15	GENERAL SCIENCE – PAPER-I (TELUGU – MEDIUM)	19T	CLICK HERE
16	GENERAL SCIENCE – PAPER-II (ENGLISH – MEDIUM)	20E	CLICK HERE
17	GENERAL SCIENCE – PAPER-II (TELUGU – MEDIUM)	20T	CLICK HERE
18	SOCIAL (ENGLISH – MEDIUM)	21E & 22E	CLICK HERE
19	SOCIAL (TELUGU – MEDIUM)	21T & 22T	CLICK HERE

AP SSC 2024 Model Paper, AP 10th Class 2024 Model Paper, AP SSC Question Paper 2024 Pdf Download, AP 10th Class Model Paper 2024 Pdf, AP SSC Previous Question Papers Pdf, AP SSC Model Question Papers.

Access to a diverse set of AP 10th Class Social Model Papers Set 7 ensures a well-rounded preparation strategy.

AP 10th Class Social Model Paper Set 7 with Solutions

Time: 3.15 hours
Max.Marks: 100

Instructions:

1. In the duration of 3 hours, 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the separate booklet only.
3. Question paper consists of 4 Sections and 33 Questions.
4. Internal choice is available in Section IV only.
5. Answers shall be written neatly and legibly.

Section-I
12 × 1 = 12 M

Note:
1) Answer all the questions.
2) Each question carries 2 marks.

Question 1.
Where is Mawkdok Dympep Valley located?
Answer:
Meghalaya State

Question 2.
Identify the wrongly matched pair and write ¡t in the answer booklet.

primary  Sector	Fishing
Secondary Sector	Mining
Tertiary Sector	Banking

Answer:
Secondary Sector – Mining. (Mining comes under primary sector)

Question 3.
Write any three environmental issues.
Answer:
The environmental issues are deforestation, soil erosion, lowering groundwater levels, increasing pollution, pressure on grazing land, rising dependence on fossil fuels, industrial emissions, use of chemical fertilizers or pesticides, etc.

Question 4.
Census is about to start in India soon.
‘A’ says that this census shows age structure, gender ratio, and literacy rate.
‘B’ says that it shows the size and density of population. Who is correct?
‘A only
B only
A & B
None of the above
Answer:
Both A & B

Question 5.
Poorest of the poor have a provision to get 35 kgs of grains per month under PDS. Name the ration card related to this.
Answer:
Antyodaya Cards

Question 6.
Which of the following places is nearer to the equator?
Trivandrum
Kanyakumari
Chennai
Answer:
The place nearer to the equator is -Kanyakumari

Question 7.
Expand U.S.S.R
Answer:
U.S.S.R – “Union of Soviet Socialist Republic”.

Question 8.
The relation between the items in the first pair is the same with those in the second pair. Find out the missed item of the second pair. Vietnam : France:: India:?
Answer:
Vietnam : France:: India: Britain.

Question 9.
Which regions are good absorbers of sunlight?
Answer:
Heavily vegetated regions.

Question 10.
In which state was the Anti-Hindi agitation started?
Answer:
Tamil Nadu.

Question 11.
The chairman of the Constitutional Drafting Committee was ……………….. .
Answer:
B.R. Ambedkar.

Question 12.
Based on the information given below, answer the question that follows.

Beginning of First World War	Russian Revolution	Treaty of Versailles	Break out of Second World War	German Invasion of USSR
1914	1917	1919	1939	1942

Q. Nitme the country which withdrew from the World War I before the War.
Answer:
Russia

Section – II
8 x 2 = 16 M

Note:
1) Answer all the questions.
2) Each question carries 2 marks.

Question 13.
Distinguish between population growth and population change.
Answer:

Population growth	Population change
1. Increase in population per annum.	Difference in number of inhabitants of a country during specific period.
2. Population growth is the difference between birth rate and death rate plus migration per year.	Population change is the number of people added to the total population in year.
3. It is expressed in percentage.	It is expressed in the addition of number of people.
4. Population growth refers to the increase in the number of inhabitants of a region during specific period of time.	This refers to the change in the distribution and composition of size of population during a specific period of time.

Question 14.
Give examples of the criterion for the measurement of human development.
Answer:
In measuring human development, the criteria taken into consideration are

• per capita income
• education
• health
• Electricity
• housing
• Life expectancy.

Question 15.
Plot the below information on a bar graph (rough).

Year	Cultivated area (in million hectares)
2000	140
2010	140

Answer:

Question 16.
Observe the below world map which is based on the basis of population and answer the question that follows.

Q. Asian Continent looks the largest in the above map. Why?
Answer:

1. Asia has the largest populous countries like China and India.
2. These two countries occupy the first two places as the highest populous countries.
3. This world map has been drawn on the basis of population.
4. So, the Asian continent looks big when comparing with other continents.

Question 17.
Mention any two environmental problems faced by Nigeria.
Answer:
Environmental problems faced by Nigeria:
Reckless oil extraction without care for the environment by foreign oil companies in Nigeria has created havoc in coastal environment.

1. Oil spillage from oil wells has a major impact on the ecosystem. Large tracts of the mangrove forests, which are especially susceptible to oil, have been destroyed.
2. Spills destroy crops and aquaculture through contamination of the groundwater and soils.

Question 18.
Explain how RTI Act enriches the democracy.
Answer:

1. It ensures the availability of all types of information to the citizen.
2. Democracy requires informed citizens.
3. Information should be transparent.
4. This can help to control corruption and make the governments accountable Thus RTI act enriches democracy.

Question 19.
Observe the following table and answer the given questions.
Coalition Governments and some political parties from 1980’s

1) What are the governing parties from 1989 – 1990?
2) What are the parties in NDA?
Answer:
1. Janatha dal,DMK, AGP,TDP and Jammu Kashmir National Conference (JKNC), etc.
2. JDU,SAD, AIADMKJKNC,Trinamool Congress,Biju Janta Dal and Shiv Sena

Question 20.
” I Have a dream that my four little children will one day live in a nation where they will not be judged the colour of their skin but by’ the content of their character…. Dr. Martin Luther King Jr.
Express the sensitivity in this speech.
Answer:
In this speech the intention of Jr. Martin Luther King is to achieve equality for all people through peaceful means. He expected that the government should ban segregation gradually on blacks by their colour and give them opportunity based on their intelligence.

Section – III
8 × 4 = 32 M

Note:
1) Answer all the questions.
2) Each question carries 4 marks.

Question 21.
What suggestions do you give to maintain friendly relations with neighbouring countries?
Answer:
The following are the suggestions for maintaining friendly relations with neighbouring countries:

• Following the ideals of democracy and international peace.
• Mutual understanding and respect for each other’s territorial integrity.
•  Settlement of disputes through bilateral discussions.
• Not interfering in the internal affairs of others.
• Promoting friendship and cooperation in the fields of culture, trade and technology.
• Restoring diplomatic relations.
• Reducing arms.
• Sharing of technological innovations.
• Organising cultural festivals.

Question 22.
Explain the role of schooling played in Vietnam National movement?
Answer:

1. Vietnamese was taught in French.
2. While teaching, Vietnamese teachers quietly modified the text and criticised what was stated by the French.
3. Students were inspired by patriotic feelings and the conviction that it was the duty of the educated to fight for the benefit of the society.
4. Many students went to Japan, China, France, USSR to study and learn about new ideas.

Question 23.
Observe the following table and analyse it.
Seat share of various political parties in 1952 and 1962

Political Party	1952	1962
1.Indian National Congress	364	361
2. Communist Party of India	16	29
3. Independents	37	20
4. Socialist Party	12	06
5. Others	38	27

Answer:

• The table shows the seat share of various political parties in 1952 and 1962 Loksabha elections.
• In first general elections held in 1952, 1957 and 1962. the Indian National Congress won reducing other parties to almost nothing.
• It was the one-party domination in political system. The Congress consistently won over 70% of the seats by obtaining about 45% of the total votes cast between 1952-1962.
• The opposition parties posed only a latent and not a real threat.
• This period helped to a large extent to nurture democracy in its early years allowing the establishment of a multi-party system based on free and open competition.

Question 24.
Based on the map given below, name any four states which record average temperatures more than 15 degrees in the month of January.

Answer:
The states which record average temperatures of more than 15 degrees in the month of January:

1. Gujarat
2. Madhya Pradesh
3. Chattisgarh
4. Odisha
5. Goa
6. Kamataka
7. Kerala
8. Tamil Nadu

Question 25.
Write any Two welfare programmes launched by present Government of India.
Answer:
The welfare programmes launched by present Government of India are

1. Sukanya Samrudhi Yojana.
2. Prime Minister Jeevan Jyothi Bhima Yojana.
3. Mahatma Gandhi National Rural Employment Guarantee Act
4. Atal Pension Yojana.

Question 26.
Write about the League of Nations.
Answer:
League of Nations:

1. The Treaty of Versailles set up the League of Nations.
2. The League of Nations had 58 members in its peak stage in 1934.
3. The President of America, Woodrow Wilson took an active role in the set up of League of Nations.
4. The League of Nations also set up health, labour welfare organisations and an International Court of Justice.
5. The League of Nations failed to prevent Germany and Italy from violating international agreements and attacks as it had no army.

Question 27.
Mention the Constitutional provisions that facilitate social change.
Answer:

1. The Constitution has many provisions facilitating social change.
2. The abolition of Untouchability.
3. The provision for reservations for Scheduled Castes and Scheduled Tribes in the Constitution.
4. Voting rights to all citizens.
5. The reservation of seats in legislatures and in public sector jobs.
6. The right of religious minorities to run their own educational institutions etc.,

Question 28.
Explain the role played by women in Anti Arrack movement in the then Andhra Pradesh.
Answer:
Role of women in Anti arrack movement in the Andhra Pradesh:

1. The women m Dubagunta village, Nellore read Sitamma’s story” Adavallu kamacite” in evening school and got inspired.
2. So next day, hundréds of them marched out of the village and stopped a cart of toddy.
3. They told the owner to throw away the liquor and he was terrified.
4. In several villages, liquor shops had to face picketings,throwìng out liquor packets and the alcohol was set on fire. Only women did all these things.
5. After innumerable meetings and protests by women across the state, arrack was officially banned by the government in 1993 and total prohibition was implemented in 1995.
6. This is really a great achievement of women who are uneducated and are of rural background.

Section-IV
5 x 8 = 40 M

Note:
1) Answer all the questions.
2) Each question carries 8 marks.
3) Each question has internal choice.
4) In question no.33, both A and B (India snap and World map) should be answered separately.

Question 29.
A) Describe the occupational structure of Indian Economy.
(OR)
B) ‘Most children of migrant families become drop-outs. Do you agree with this statement? Justify your answer.
Answer:
A) The distribution of working population among different occupations or productive activities is known as occupational structure.
1. Primary Sector:
Agriculture, fishing, plantations, mining and allied activities are included in primary occupations.
2. Secondary Sector:

• industries both large and small comprise this sector. Construction is also included in this sector.
• This sector showed a tremendous increase in the last 37 years.

3. Tertiary Sector:

• Occupation services like, Banking, Insurance, Telecommunications, etc., come under tertiary sector or service sector.
• The shares of service sector in employment and CDP are 25% and 57% respectively.

B)

1. Yes, I agree with the above statement
2. When families migrate, children also accompany them to their destination.
3. The children who are at present studying in a school in their native village need to discontinue their studies and migrate along with their parents.
4. These migrated children are not able to continues their studies at the new place due to financial problems and strange atmosphere in the new place.
5. Schools in their native place refuse to take them again when they come back. So, finally, most of the children become drop-outs.

Question 30.
A) Describe the cycle of the monsoon patterns in India.
(OR)
B) How are human activities contributing to global warming?
Answer:
A)

1. 1. The climate of India can be described as tropical monsoon type. The word ‘monsoon’ has been derived from the Arabic word ‘mausam’ which conveys the rhythm of seasons and the changes that occur in the direction of winds and in the distribution of rainfall and temperature with the change of seasons.
2. 2. Monsoon winds are caused by thermal Contrast between the inter-tropical convergence zone and the upper air circulation.
3. 3. An intensive low pressure develops on the land surface during the summer season. It draws air from the high-pressure region of the seas Leading to the southwest monsoons.
4. 4. During the winter, the pressure conditions in the area are reversed and so are the winds. This time low-pressure system develops in the seas which draws air from the landmass particularly blowing from northeast side and form the north-east monsoons.

(OR)

1. Global warming is occurring since the Industrial Revolution.
2. More and more of greenhouse gases are released due to industrialization.
3. Burning of fossil fuels by humans also increased global warming.
4. Radiation created by the humans also causes global warming.
5. The release of chiro-fluoro carbons also led to global warming.
6. Deforestation i.e. cutting down of trees is one of the human activities that contributes to global warming.
7. Excessive use of vehicles releases much carbon-di-oxide which contributes to air pollution. Arid that, in turn, causes global warming.

Question 31.
A) Hitler said, “We do not consider it correct for the woman to interfere in the world of the man, in his main sphere” – How far are his words justifiable? Give your opinion.
(OR)
B) Describe the present circumstances, that are threatening world peace.
Answer:
A)

1. The words of Hitler are not justifiable.
2. In the view of Hitler, men and women belong to a distinct world.
3. Women should be confined have bringing up children and to bear pain and suffering.
4. of course, as a social norm, it was in practice that men make out a living and women are entrusted the responsibility of the children.
5. But, now the scenario changed. Nowadays women came into every field and succeeded.
6. They are in every sphere. They are not only holding household activities but they are also the bread winners for the family.
7. In some institutions, they are in key positions also. They are ruling the governments. In my view, we have to respect every woman.

(OR)
B) Present circumstances that are threatening world peace

• Terrorism
• Wars
• Armament race
• Invasions
• Communalism
• Exploitation of resources
• Interference of developed countries in the affairs of developing countries
• Aggressive nationalism

Question 32.
A) Observe the below bar graph and analyse it.

(OR)
B) Based on the information given answer the questions.
i) Who won the Second World War?
ii) What was the immediate provocation of World War II?
iii) Mention the superpower that joined late in the World War II.
iv) Name the person who was mainly responsible lot the mass murder of the Jews

Answer:
A)

1. The constitution makers were aware that laws will have to be amended from time to time.
2. The makers laid down the provisions for amending the laws and the articles in the constitution.
3. Since the constitution came into force on 26th January 1950 till 2013, nearly 99 amendments were made to make successful functioning of our democracy.
4. During the decades 1971-1990, maximum amendments were made.
5. One major amendment to the constitution was made in 1970 including the words ‘Secular and ‘Socialist to the preamble. ‘
6. However, certain basic principles on which the nation continues to exist cannot be amended.

(OR)

B)

• Allied Forces.
• Germany’s invasion of Poland
• USA
• Adolf Hitler.

Question 33.
A) Mark the following on the outline map of India.
i)
1) Delhi
2) Lakshadweep islands
3) River Godavari
4) Arunachal Pradesh
(OR)
ii)
1) Aravalis
2) River Krishna
3) Sikkim
4) Indian Ocean
Answer:
a)
1) Delhi
2) Lakshadweep islands
3) River Godavari
4) Arunachal Pradesh
(OR)
b)
1) Aravalis
2) River Krishna
3) Sikkim
4) Indian Ocean

B) Mark the following on the outline map of the world.
i)
1) Egypt
2) Portugal
3) China
4) USA
(OR)
ii)
1) Mediterranean Sea
2) Srilanka
3) Equator
4) France
Answer:
a)
1) Egypt
2) Portugal
3) China
4) USA
(OR)
b)
1) Mediterranean Sea,
2) Srilanka
3) Equator
4) France

Access to a diverse set of AP 10th Class Social Model Papers Set 6 ensures a well-rounded preparation strategy.

AP 10th Class Social Model Paper Set 6 with Solutions

Time: 3.15 hours
Max.Marks:100

Instructions:

1. In the duration of 3 hours, 15 minutes, 15 minztes of time is allotted to read the question paper.
2. All answers shall be written in the separate booklet only.
3. Question paper consists of 4 Sections and 33 Questions.
4. Internal choice is available in Section IV only.
5. Answers shall be written neatly and legibly.

Section – I
12 x 1 = 12 M

Note:
1) Answer all the questions.
2) Each question carries 1 mark.

Question 1.
Find the odd one out with regard to reducing the differences In sex ratio.
Education
Child marriages
Infanticides
Superstitions
Answer:
Education

Question 2.
River Ganga has twin sources.
Fill the box.

Answer:
Bhagiradhi

Question 3.
What is the river shown with’?’
Answer:

River Brahmaputra

Question 4.
What is the book ‘Before they pass away’ about?
Answer:
Extinction of nomadic communities.

Question 5.
Identify the wrong statement.
1. If we go towards poles from equator, temperatures increase
2. South of Tropic of Cancer is in tropical region
3. Surface temperatures depend on insolation.
Answer:
1. (If we go towards poles from the equator, temperatures increase)

Question 6.
The pyramid shows the order of settlements.
What is the highest level?

A) Revenue villages
B) Metropolitan cities
C) Megacities
D) Towns
Answer:
C. (Megacities)

Question 7.
Who is the prime minister that abolished privy purses?
Answer:
Indira Gandhi

Question 8.
The 3R’ s in ‘New Deal’ policy reveals
i) Reforms
ii) Relief
iii) …………………….. .?
Answer:
Recovery

Question 9.
If you want to travel to Mexico from Greenland, in which direction you have to travel?
Answer:
South direction

Question 10.
Arrange the following in a chronological order
(a) Simia agreement;
(b) Tashkent agreement;
(c) Indo-China War.
Answer:
(c) Indo-China War.
(b) Tashkent agreement;
(a) Simia agreement;

Question 11.
Choose the incorrect matching.
i) George Orwell – AnimaI Farm
ii) Roosevelt – New Deal Policy
iii) Silent Spring – Bava Mahalia
Answer:
(iii) Silent Spring – Bava Mahalia (Silent Spring is written by Rachel Carson about the impacts of DDT on living beings.)

Question 12.
Identify the ‘?

Answer:
Hausa – Fulani

Section – II
8 × 2 = 16 M

Note:
1) Answer all the questions.
2) Each question carries 2 marks.

Question 13.
MGNREGA is a scheme for providing rural employment. Mention some other schemes that are meant for providing employment.
Answer:
jawahar rozgar yojana, DWACRA, PMEGP (Prime Minister Employment Generation
Programme)
SGSY (Swarna Jayanti Gram Swaroz-gar Yojana)

Question 14.
Mention any two reasons for more employment in the agriculture sector.

Answer:

• Not enough jobs were created in industry and service sectors.
• No need of literacy in agriculture compared to the other sectors.
• No need of skill as agriculture is more traditional.

Question 15.
Why did the people oppose the establishment of Kudankulam Nuder power project in Tamilnadu?
Answer:
The people of Kudankulam have protested against the Nuclear power project on the grounds of safety, security, and livelihood.

Question 16.
Objectives of liberalisation are appreciable. Write any two appreciable facts.
Answer:

1. Removing the obstacles in the process of economic development.
2. Widening the scope of the private sector.

Question 17.
Though Hitler was the main responsible person for the Second World War, to which of his characteristics, the Germans get attracted?
Answer:
The Germans got attracted to

• Hitler powerful attracting speeches
• His promises to restore the dignity of Germany
• His promises to build a strong Germany.

Question 18.
Write any two malpractices in elections that we can notice nowadays?
Answer:

1. Give cash or gif to voters.
2. Campaigning after or before the permitted hours.

Question 19.
What is the ‘two nation theory’?
Answer:
Partition of India based on religions Ilindus and Muslims.

Question 20.
Is India a ‘Republic State’?
Answer:
Yes, India is a Republic State because the head of our country is elected by the people either directly or indirectly. It is not a hereditary post.

Section – III
8 × 4 = 32 M

Note:
1) Answer all the questions.
2) Each question carries 4 marks.

Question 21.
How is environmental protection linked with our lifestyle?
Answer:

1. Use of organic agricultural farming practices.
2. Avoiding plastic usage.
3. Use of renewable energy sources.
4. Use of public transport.
5. Use of CNG.

Question 22.
Name the facilities enjoyed by the workers in the organised sector.
Answer:
The following facilities are available to workers organised sector.

1. Security of Employment.
2. Fixed number of working hours.
3. Payment for overtime work.
4. Paid leave
5. Payment during holidays
6. Provident Fund
7. Medical facilities
8. Pension
9. Safe working environment.

Question 23.
How did the settlements begin? Why did they change?
Answer:
Beginning of settlements :
Early humans were hunter-gatherers. But owing to changes in obtaining food, they started agricultural practices and this resulted in settlements.

Reasons for change:

1. Livelihoods
2. Migrations
3.  Importance of cities.
4. Weather conditions.
5. Infrastructural facilities, public amenities

Question 24.
Observe the map and answer the following questions.
1. What are the tributaries of River Indus?
2. ‘Girhills’ are situated in which state?

Answer:
1. Jhelum, Chenab, Ravi and Sutlej
2. Gujarat

Question 25.
What is your opinion about the decisions made by Mountbatten in February 1947 before independence?
Answer:

1. In February 1947, Mountbatten replaced Wavell and became the Vicerc Mount Batten started one last round of talks to find a solution to the granting of free to our nation.
2. When these talks also failed, he announced that British India would become freed but also would be divided.
3. In my opinion, this solution was the Only workable solution to end the riots, bloodshed and hatred that people were filled with.

Question 26.
Write about ‘Operation Blue Star’.
Answer:
Sikh militants under the leadership of Bhind Ranwale attacked non-Sikh population in Punjab. This Sikh separatist group hid in Golden Temple, a holy place for all Sikhs. Army was called to take action to subdue those militants and vacate the campus. This operation was called Operation Blue Star.

Question 27.
Why did anti-Hindi agitation start? Write about its consequences.
Answer:

1. When the Official Languages Act was passed in 1963, the Tamilnadu party D.M.K believed that it was an attempt to foist Hindi On the rest of the country. They started anti-Hindi agitation consequences.
2. When things seemed to be going out of hand, Lal Bahadur Shastri, made a series of concessions to assuage the feelings of the anti-Hindi camp.
3. These included among others, the right of each state to have a language of its own.
4. English would continue to be the communication language.
5. Thus, we can see how a popular social movement forced the government of the day to reconsider the official position.

Question 28.
If a constitution for the entire school had to be drafted who all have to be involved in it?
Answer:
If a constitution for the entire school had to be drafted, the following members are to be involved in it.

1. Student representatives of both genders from all classes.
2. Headmaster of the school.
3. Teaching and non-teaching staff of the school.
4. Members of school management committee.

Section – IV
5 x 8 = 40 M

Note:
1) Answer all the questions.
2) Each question carries 8 marks.
3) Each question has internal choice.
4) In question no.33, both A and B (India map and World map) should be answered separately.

Question 29.
A) Read the given paragraph and comment. In many parts of the country, girls’ education is still given less priority by the parents as compared to boys’ education. While girls may study for a few years, they may not complete their schooling.
(OR)
B) Read the given paragraph and interpret.
Labour being the most abundant factor of production, it would be ideal if the new ways of farming used much more labour. Unfortunately, such a thing has not happened use of labour on farms is limited. The labour, looking for opportunities is thus migrating to neighbouring villages, towns and cities. Some labour has entered the non-farm sector in the village.
Answer:
A)

1. Education is very important for every child whether boy or girl. It is sad that some communities still discriminate against the education of the girl child.
2. The biggest hurdle is the prejudices families have about girls that girls are slow learners, they are not rational, they are to be confined inside the domestic household.
3. By sending a girl to school, she is far more likely to ensure that her children also receive education.
4. Children of educated women are less likely to die before their first birthday. Primary education also helps to reduce infant mortality rate.

B)

1. Agricultural labourers are widely scattered over large number of villages in the country and so cannot be effectively organised.
2. Villagers are generally unskilled workers carrying on agricultural operations at a very low wage.
3. The agricultural labourers are one of the most exploited and oppressed classes in rural areas.
4. They have to face the problems of unemployment and underemployment.

Question 30.
A) What is the influence on society when female percentage decreases in sex ratio?
(OR)
B) Give solutions to address the urbanization problems.
Answer:
A)

1. Sex ratio is the number of females per 1000 males in the population.
2. This information is an important social indicator to measure the extent of equality between men and women in a society.

The following are the effects of low sex ratio:

1. Sex ratio is a cause of concern since it indicates a hidden form of discrimination.
2. Women and girls iii particular face inequal opportunities for education and development.
3. Sex ratio also shows the discrimination of women in the male-dominated society.
4. Many of the girl children are married even before the age of marriage is reached. This is causing the early childbirth for the girl and as a result the girl is not only losing her childhood but also her health.

Question 31.
A) Observe the following table and answer the questions given below.

a) When was the first coalition government formed in India?
b) Which party was a partner of government in all the three coalition governments?
c) Which state does Trinamool Congress belong to?
d) What is the difference between political parties becoming partners in the coalition government and supporting the government?
(OR)
B) Observe the following bar graph and answer the questions given below.
a) Prepare a table with the information given in the bar graph.
b) Mention names of the six countries which increased 300% of investment on military from 1880-1914.
c) What is the relationship between industrialisatioñ and armaments race?

Answer:
A)
a) In 1989 the first coalition government led by VP Singh’s Janata Dal was formed in India.
b) Jammu and Kashmir National Conference.
c) West Bengal
d) The political parties becoming partners in the coalition government can be ministers in the cabinet. They are binded over by the policies of the government The parties supporting the government do not take part in the ministry or cabinet The parties supporting the government give issue-based cooperation only.

B)
a)

Year	Expenditure (in million pounds)
1880	132
1890	158
1900	205
1910	288
1914	397

(b) Germany, Austria-Hungary, Great Britain, Russia, Italy and France.

(c) Relationship between industrialisation and armaments race:

• Industrialisation led to overproduction. This made the industrial powers to search markets to sell their production and to get raw materials. This created lot of tension among the countries to suppress one another through wars.
• All these industrial countries competed with one another leading to wars and decrease in military expenditure.
• A large industry of weapons emerged due to industrialisation. They constantly promoted the idea of using war as a solution to diplomatic problems.

Question 32.
A) Write about the great economic depression.
(OR)
B) Read the following paragraph and interpret the changes taken place in social and economic fields in India.
Land reforms were implemented in a half-hearted manner across India. While Zamindari system was abolished, redistribution of land to landless did not take place. The rich and powerful in the rural areas continued to control most of the land. The Dalits continued to be landless but benefitted from the abolition of forced labour and abolition of untouchability.
Answer:
A)

1. The Great Depression began around the end of 1929 and lasted almost till 1939 when the Second World War began. During this decade there was a worldwide economic decline triggered by a decline in Iemand and faU in prices.
2. As many as 25% of Americans were unemployed and nearly 33% in many other countries. As factories closed down and trade declined, cities became centres of decline.
3. This in turn caused a collapse of prices up to 60% on agricultural produce causing pauperisation of millions of farmers and stopping of cultivation.
4. It had devastating social consequences, increasing poverty, desolation and’ homelessness etc.

Question 33.
Locate the following In the given map of India.
A)
a)
1) A peninsular river
2) Mumbai
3) Himalayan mountains
4) Circar coast
(OR)
b)
1) Vindhya mountains
2) One summer resort
3) Chennai
4) Arunachal Pradesh
Answer:
A)
a)
1) A peninsular river: R. Godavari
2) Mumbai
3) Himalayan mountains
4) Circar coast
(OR)
b)
1) Vindhya mountains
2) Chennai
3) Ooty
4) Arunachal Pradesh

B)
a) Locate the following on the given world map.
1. China
2. Vietnam
3. France
4. USSR
(OR)

b)
1) The ocean in which Japan is existing.
2) The nearest group of islands to Taiwan
3) The country where Igbo tribe lives.
4) The city in which UNO headquarters is situated.
Answer:
B)
a)
1) China
2) Vietnam
3) France
4) USSR
(OR)
b)
1) Pacific Ocean
2) Philippine Islands
3) Nigeria
4) New York