TS 10th Class Maths Question Paper April 2023

The strategic use of TS 10th Class Maths Model Papers and TS 10th Class Maths Question Paper April 2023 can significantly enhance a student’s problem-solving skills.

TS 10th Class Maths Question Paper April 2023

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. Answer all the questions under Part – A on a separate answer book.
2. Write the answers to the questions under Part – B on the question paper itself and attach it to the answer book of Part – A.

Part – A (60 Marks)
Section – I (6 × 2 = 12 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 1.
Find the centroid of the triangle whose vertices are (2, 3) (-4, 7) and (2, -4).
Answer:

Question 2.
Find the probability of getting a ‘vowel’ if a letter is chosen randomly from the word “INNOVATION’.
Answer:
P(E) = \(\frac{\text { Number of favourble outcomes }}{\text { Number of total outcomes }}\)
Favourable outcomes = i, o, a, i, o
Number of favourable outcomes = 5.
Number of total outcomes = 10
P(getting a vowel) = \(\frac{5}{10}\) = \(\frac{1}{2}\)

Question 3.
Express ‘tan θ’ in terms of ‘sin θ’.
Answer:
‘tan θ’ = \(\frac{\sin \theta}{\cos \theta}\)
sin² θ + cos² θ = 1
cos θ = 1 – sin² θ
cos² θ = \(\sqrt{1-\sin ^2 \theta}\)
∴ tan θ = \(\sqrt{\frac{\sin \theta}{1-\sin ^2 \theta}}\)

Question 4.
“An observer standing at a distance of 10m from the foot of a tower, observes its top with an angle of elevation of 60°.” Draw a suitable diagram for this situation.
Answer:
AB – Tower
C – Position of observer
60° – Angle of elevation

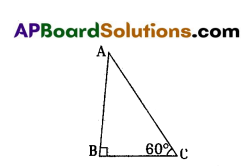
Question 5.
The sides of a triangle measure 2√2, 4 and 2 √6 units. Is it a right-angled triangle ? Justify.
Answer:
(2√2)² = 8
(4)² = 16
(2√6)² = 24, (2√2)² + (4)² = (2√6)²
∴ If sum of squares of two sides of a triangel is equal to the square of the third side, then the triangle is a right angled triangle. (Converse of Pytha groups theorem)
∴ Given triangle is a right – angled triangle.

Question 6.
Solve the quadratic equation 2 sin² θ – 3 sin θ + 1 = 0, where 0° < θ ≤ 90°.
Answer:
2 sin² θ – 3 sin θ + 1 = θ
where 0° < θ ≤ 90°
2 sin² θ – 2 sin θ – sin θ + 1 = θ
2 sin θ (sin θ – 1) – 1 (sinθ – 1) = 0
(2 sin θ – 1) (sin θ – 1) = 0

2 sin θ – 1 = 0
2 sin θ = 1
sin θ = \(\frac{1}{2}\)
sin θ = \(\frac{1}{2}\) = sin 30°
θ = 30°

sin θ – 1 = 0
sin θ = 1
sin θ = 1 = sin 90°
θ = 90°

Section – II (6 × 4 = 24 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 7.
Write the formula for Median of a grouped data and explain each term of it.
Answer:
Median = l + \(\left[\frac{\frac{n}{2}-c f}{f}\right]\) × h
l = lower boundary of median class.
n = number of observations.
cf = cumulative frequency of class preceding the median class.
f = frequency of median class.
h – class size.

Question 8.
If x² + y² = 10xy, then prove that 2 log (x + y) = logx + logy + 2 log 2 + log3.
Answer:
Given equation x² + y² = 10xy
Adding 2xy on both sides
x² + y² + 2xy = 10xy + 2xy
(x + y)² = 12xy
Applying log on both sides
log (x + y)² = log (12xy)
2 log (x + y) = log 12 + log x + log y
∴ 2 log (x +y) = log 4 + log 3 + log x + log y
Hence proved.

Question 9.
A strip of width 4 cm is attached to one side of a square to form a rectangle. The area of the rectangle formed is 77 cm², then find the length of the side of the square.

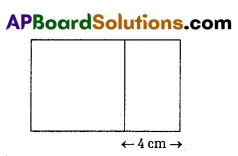
Answer:
Let the side of the square be ‘x’ cm.
Then length of rectangle = x + 4 cm
Breadth of rectangle = x = cm

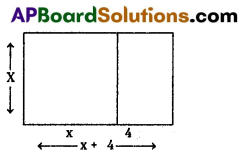
Area of rectangle = length × breadth
= (x + 4) x

Question 10.
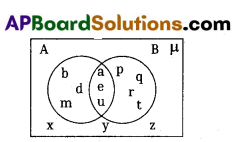
From the given Venn diagram šhow that n (A∪B) = n (A) + n (B) – n (A∩B).

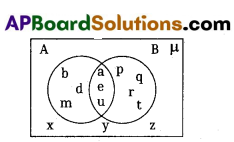
Answer:
A – { b, d, m, a, e, u},
B = {a, e, u, p, q, r, t}
(A∪B) = {b, d, m, a, e, u, p, q, r, t}
(A∩B) = {a, e, u}
n (A) = 6, n (B) = 7
n (A ∪ B) = 10, n (A∩B) = 3
LHS n (A ∪ B) = 10
RHS n (a) + n (B) – n(A∩B)
= 6 + 7-3 = 13-3 = 10 LHS = RHS
∴ n (A∪B) = n (A) + n(B) – n (A∩B)

Question 11.
A box contains four slips numbered 1, 2, 3, 4 and another box contains five slips numbered 5, 6, 7, 8, 9. If one slip is taken randomly from each box,
i) How many number pairs are possible ? ,
ii) What is the probability of both being odd ? „
iii) What is the probability of getting the sum of the numbers 10 ?
Answer:
i) Possible number pairs
(1, 5) (1, 6) (1, 7) (1, 8) (1, 9)
(2, 5) (2, 6) (2, 7) (2, 8) (2, 9)
(3, 5) (3, 6) (3, 7) (3, 8) (3, 9)
(4, 5) (4, 6) (4, 7) (4, 8) (4, 9)
Number of possible number pairs = 20

ii) Favourable outcomes (1, 5), (1,7), (1, 9), (3, 5), (3,7), (3, 9)
Number of favourable outcomes = 6
P (getting both being odd)
= \(\frac{\text { Number of favourable outcomes }}{\text { Total number of outcomes }}\)
= \(\frac{6}{20}\) = \(\frac{3}{10}\)

iii) Favourable outcomes (1, 9), (2, 8) (3, 7), (4, 6)
Number of favourable outcomes = 4
P (getting the sum of the numbers 10)
= \(\frac{4}{20}\) = \(\frac{1}{5}\)

Question 12.
Which term of the A.P. 21, 18, 15, ………………. is – 81 ? Also find the term which becomes zero.
Answer:
Arithmetic progression 21, 18, 15, ……..
a = 21; d = 18 – 21 = -3; a_n = -81
n = ?
a_n = a + (n – 1) d
– 81 = 21 + (n – 1) (- 3)
(n – 1) (- 3) = – 81 – 21 = – 102
n – 1 = \(\frac{-102}{-3}\) = 34
n = 34 + 1 = 35
-81 is 35^th term of that A.P.
again a_n = 0; n = ?
⇒ a_n = a + (n – 1) d
0 = 21 + (n – 1) (- 3)
(n – 1) (- 3) = – 21
n- 1 = \(\frac{-21}{-3}\) = 7
n – 1 = 7 ⇒ n = 7 + 1 = 8
∴ 8^th term of that A.P. is zero.

Section – III (4 × 6 = 24 Marks)

Note :

1. Answer any 4 questions from the given six questions.
2. Each question carries 6 marks.

Question 13.
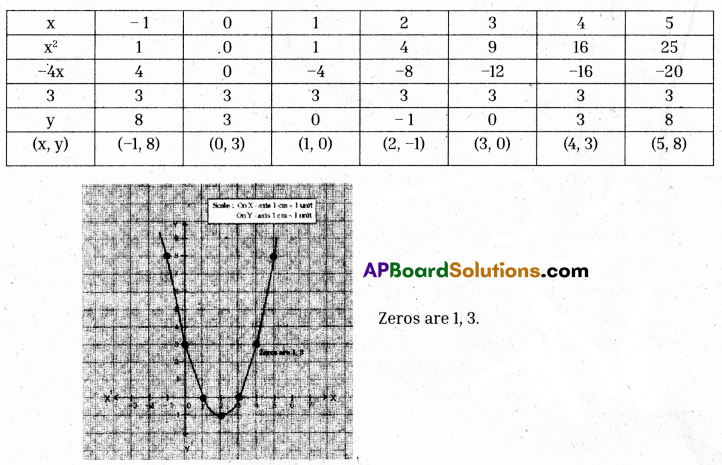
Draw the graph of the quadratic polynomial p(x) = x² – 4x + 3 and find the zeroes of the polynomial from the graph.
Answer:
y = p(x) = x² – 4x + 3

Question 14.
In an acute angled triangle ABC, if sin (A + B – C) = \(\frac{I}{2}\) and cos (B + C – A) = \(\frac{I}{2}\), then find ∠A, ∠B and ∠C.
Answer:
sin (A + B – C) = \(\frac{I}{2}\) = sin 30°
⇒ A + B – C = 30° ………….. (1)
cos (B + C – A) = \(\frac{I}{2}\) = cos 60°
⇒ B + C – A = 60° ……………. (2)
On adding equations (1) and (2)

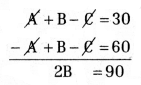
⇒ B = \(\frac{90}{2}\) = 45°
Substituting the value of B in equation (2)
C – 4 = 60° – 45° = 15° ………………. (3)
B + C + A = 180°
(sum of angles of a triangle)
C + A = 180° – 45° = 135° …………….. (4)
Now solving equations (3) and (4)

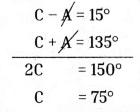
∠A = 135° – 75° = 60°
∠A = 60°, = 45°, ∠C =75°

Question 15.
Find the mode for the following data.

Answer:

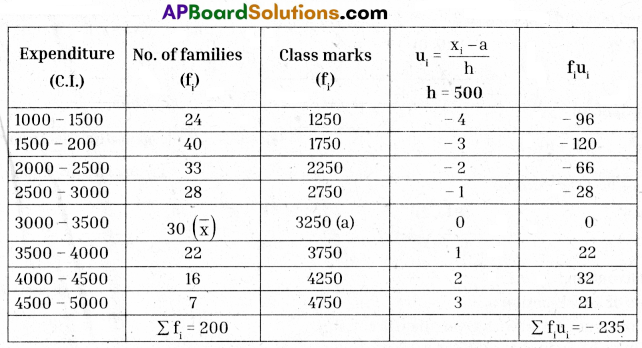
since the maximum families 40 lies in the class 1500 – 2000, this is the required modal class.
Lower boundary of the modal class (l) = 1500
Frequency of the modal class (f₁) = 40
Frequency of the class preceding the modal class f₀ = 24
Frequency of the class succeeding the modal class f₂ = 33
Height of the class, h = 500
Model (Z) = l + \(\frac{\left[\mathrm{f}_1-\mathrm{f}_0\right]}{2 \times \mathrm{f}_1-\left[\mathrm{f}_0+\mathrm{f}_2\right]}\) × h = 1500 + \(\frac{40-24}{2 \times 40-(24+33)}\) × 500
= 1500 + \(\frac{16 \times 500}{80-57}\) = 500 + \(\frac{8000}{23}\) = 1500 + 347.826 = ₹ 1847.83
Hence, modal monthly income = ₹ 1847.83
Assumed mean (a) = 3250
Σf_i = 200; Σu_if_i = – 235
Mean monthly income= \(\bar{x}\) = a + \(\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}\) × h = 3250 – \(\frac{235}{200}\) × 500

Question 16.
If A (-2, 2), B (a, 6), C (4, b) and D (2, -2) are the vertices of a parallelogram ABCD, then find the values of a and b. Also find the lengths of its sides.
Answer:

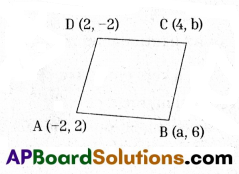
Vertices of parallelogram ABCD are
A (-2, 2), B (a, 6), C (4, b), D (2, -2)
Mid point of AC = (\(\frac{-2+4}{2}, \frac{2+b}{2}\)) = (1, \(\frac{2+b}{2}\))
Mid point of BD = (\(\frac{a+2}{2}, \frac{6-2}{2}\)) = (\(\frac{a+2}{2}\), 2)
Since it is a parallelogram, mid-points of diagonals coincide.
So, (1, \(\frac{2+b}{2}\)) = (\(\frac{a+2}{2}\), 2)
\(\frac{1}{1}\) = \(\frac{a+2}{2}\)
a + 2 = 2
a = 2 – 2 = 0

\(\frac{2+b}{2}\) = \(\frac{2}{1}\)
2 + b = 4
b = 4 – 2 = 2

Question 17.
Construct triangle ABC with BC = 7 cm, ∠B = 45° and ∠C = 60°. Then construct another triangle similar to Δ ABC, whose sides are \(\frac{3}{5}\) times of the corresponding sides of Δ ABC.
Answer:

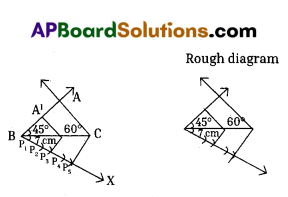
Construction:
Steps of Construction:

1. Construct Δ ABC with given measurements.
2. Draw \(\overrightarrow{\mathrm{BX}}\) such that ∠CBX is an acute angle.
3. Locate points P₁, P₂, P₃, P₄, P₅ on \(\overrightarrow{\mathrm{BX}}\) such that
   BP₁ = P₁P₂ = P₂P₃ = P₃P₄ = P₄P₅
4. Joint P₅ and C.
5. Draw a parallel line to P₅ C through P₃to meet BC at C¹.
6. Draw a parallel line to AC through C¹ to meet BA at A¹.
7. Δ A¹ BC¹ is required similar triangle.

Question 18.
Prove that 2√3 + √5 is an irrational number.
Answer:
To Prove: 2√3 + √5 is an irrational number. On contrary, let us suppose that 2√3 + √5 be a rational number. ”
Then 2√3 +√5 = \(\frac{\mathrm{p}}{\mathrm{q}}\)
squaring on both sides, we get (2√3 + √5)² = (\(\frac{\mathrm{p}}{\mathrm{q}}\))²
(2√3)² + (√5)² + 2 (2√3) (√5) = \(\frac{p^2}{q^2}\)
12 + 5+ 4\(\sqrt{15}\) = \(\frac{p^2}{q^2}\)
17 + 4\(\sqrt{15}\) = \(\frac{p^2}{q^2}\) ⇒ 4\(\sqrt{15}\) = \(\frac{p^2}{q^2}\) – 17 ⇒ \(\sqrt{15}\) = \(\frac{p^2-17 q^2}{4 q^2}\)
L H. S = an irrational number.
R. H. S = p, q being integers, \(\frac{p^2-17 q^2}{4 q^2}\)
is a rational number.

This is a contradiction to the fact that \(\overline{\mathrm{X}}\) is an irrational. This is due to our assumption that 2√3 + √5 is rational. Hence our assumption is wrong, and 2√3 + √5 is an irrational number.

Also;
(2√3 + √5) (2√3 – √5) = (2√3)² – (√5)²
[∵ (a + b) (a – b) = a² – b²] = 4 × 3 – 5 = 12 – 5 = 7, a rational number.

Part – B (20 Marks)

Note :

1. All questions are to be answered.
2. Each question carries 1 mark.
3. Answers are to be written in the Question paper only.
4. Marks will not be given for overwriting, rewriting or erased answers.

I. Write the CAPITAL LETTERS (A, B, C, D) of the correct answer in the brackets provided against each question, 20 × 1 = 20 M

Question 1.
Prime factorization of 98 is ……………. .
A) 2² × 7
B) 2² × 7²
C) 2 × 7²
D) 2³ × 7
Answer:
C) 2 × 7²

Question 2.
The 30^th term of the A.P. 10, 7, 4, ……………. is ……………….. .
A) 87
B) 77
C) -77
D) -87
Answer:
C) -77

Question 3.
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is ……………….. .
A) 5
B) 12
C) 11
D) 7 + √5
Answer:
B) 12

Question 4.
If x⁴ + 3x² + 7 is divided by x + 3, then the possible degrees of quotient and remainder are …………… .
A) 3, 0
B) 4, 1
C) 3, 1
D) 4, 0
Answer:
A) 3, 0

Question 5.
The pair of equations 9x + 3y +12 = 0 and 18x + 6y + 26 = 0 has …………… .
A) unique solution.
B) two solutions.
C) infinitely many solutions.
D) no solution.
Answer:
D) no solution.

Question 6.
“The product of two consecutive positive integers is 30”. This can be expressed algebraically as …………….. .
A) x(x + 2) = 30
B) x(x – 2) = 30
C) x(x – 3) = 30
D) x(x + 1) = 30
Answer:
D) x(x + 1) = 30

Question 7.
A cylindrical pencil sharpened at one end is a combination of ……………….. .
A) a cone and a cylinder.
B) a cone and a hemisphere.
C) a hemisphere and a cylinder.
D) two cylinders.
Answer:
A) a cone and a cylinder.

Question 8.
If a solid sphere is melted and converted into a solid cylinder, then the volume of the cylinder will ……………….. .
A) become double.
B) remains unchanged.
C) increase.
D) decrease.
Answer:
B) remains unchanged.

Question 9.
If Δ ABC is right-angled at C, then the value of cos (A + B) is ………………… .
A) 0
B) \(\frac{I}{2}\)
C) \(\frac{\sqrt{3}}{2}\)
D) 1
Answer:
A) 0

Question 10.
If the mean of a, a + 3, a + 6, a + 9 and a + 12 is 10, then the value of ‘a’ is …………………. .
A) 1
B) 2
C) 3
D) 4
Answer:
D) 4

Question 11.
A fish tank has 5 male fish and 8 female fish. If a fish is randomly taken out of it, then the probability of getting a male fish is ……………….. .
A) \(\frac{5}{8}\)
B) \(\frac{5}{13}\)
C) \(\frac{8}{5}\)
D) \(\frac{13}{5}\)
Answer:
B) \(\frac{5}{13}\)

Question 12.
The roster form of the set A = {x: x = n², n ∈ N, n < 5} is ………………….. .
A) A = {1, 4, 9, 16, 25}
B) A = {0, 1, 4, 9, 16}
C) A = {1, 4, 9, 16 }
D) A = {0, 1, 4, 9, 16, 25}
Answer:
C) A = {1, 4, 9, 16 }

Question 13.
If the zeroes of the polynomial x² + (a + 1) x + b are 2 and -3, then the values of a and b are ………………. .
A) a = -5, b = -1
B) a = 5, b = -1
C) a = -2, b = 6
D) a = 0,b = -6
Answer:
D) a = 0,b = -6

Question 14.
Among the following, the pair of triangles which are always similar is ……………… .
A) two isosceles triangles.
B) two scalene triangles.
C) two equilateral triangles.
D) two right-angled triangles.
Answer:
C) two equilateral triangles.

Question 15.
Corresponding sides of two similar triangles are in the ratio 2 : 3. If the area of the smaller triangle is 48 cm², then the area of the larger triangle is ……………… .
A) 108 cm²
B) 72 cm²
C) 36 cm²
D) 90 cm²
Answer:
A) 108 cm²

Question 16.
If the length of a tangent from an external point ‘A’ at a distance of 5 cm from the centre of the circle is 4 cm, then the radius, of the circle is ……………….. .
A) 5 cm
B) 3 cm
C) 7 cm
D) 5 + √3 cm
Answer:
B) 3 cm

Question 17.
The quadratic equation with roots 2 + √3 and 2 – √3 is ………………….. .
A) x² + 4x + 1 = 0
B) x² + 4x – 1 = 0
C) x² – 4x + 1 = 0
D) x² – 4x – 1 =0
Answer:
C) x² – 4x + 1 = 0

Question 18.
The LCM of the given numbers x and y where y is a multiple of x is …………………….. .
A) x
B) y
C) x^y
D) x + y
Answer:
B) y

Question 19.
The value of (sin 30° + cos 60°) – (sin 60° + cos 30°) is ………………… .
A) 0
B) 1 + 2√3
C) 1 – √3
D) 1 + √3
Answer:
C) 1 – √3

Question 20.
In a random experiment E and E are complementary events. If P (E) = 0.43, then P(\(\overline{\mathbf{E}}\)) is ……………….. .
A) 0.57
B) 0.43
C) 0.17
D) 1
Answer:
A) 0.57