AP 10th Class Maths Model Paper Set 4 with Solutions

Regularly solving AP 10th Class Maths Model Papers Set 4 contributes to the development of problem-solving skills.

AP SSC Maths Model Paper Set 4 with Solutions

Instructions :

1. In the duration of 3 hours 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the answer booklet only.
3. Question paper consists of 4 Sections and 33 questions.
4. Internal choice is available in section – IV only.
5. Answers shall be written neatly and legibly.

Section – I
(12 × 1 = 12M)

Note:

1. Answer all the questions in one word or phrase.
2. Each question carries 1 mark.

Question 1.
The exponent of 2 in the prime factorisation of 144, is ……..
A) 4
B) 5
C) 6
D) 3
Solution:
A) 4

Question 2.
Statement (A) : Degree of a constant polynomial is “0”.
Statement (B) : Degree of a zero polynomial is “0”.
Choose the correct answer.
i) Both (A) and (B) are TRUE
ii) (A) is TRUE, (B) is FALSE
iii) (A) is FALSE, (B) is TRUE
iv) Both (A) and (B) are FALSE
Solution:
ii) (A) is TRUE, (B) is FALSE

Question 3.
∆ABC is an isosceles triangle right angled at ‘C’ and AB² = n.AC² then, n = ……….
Solution:
2.

Question 4.
When A ⊂ B then A – B = ……………….
Solution:
φ

Question 5.
If AP and AQ are the two tangents to a circle with centre “O” so that ∠POQ = 110 then ∠PAQ = ………..

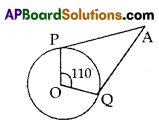
Solution:
70°

Question 6.
Match the following

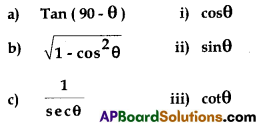
A) a – iii, b – ii, c – i
B) a – ii, b – iii, c – i
C) a – iii, b – i, c – ii
D) a – ii, b – i, c – iii
Solution:
A) A – iii, B – ii, C – i.

Question 7.
In an A.P. a = 10, d = 10 then the fourth term of A.P is ………..
Solution:
40.

Question 8.
A ladder of length x metres is leaning against a wall making an angle θ with the ground. Which trigonometric ratio would you like to consider to find the height of the point on the wall at which the ladder is touching ?
Solution:
Relevant diagram for the problem, Clearly hypotenuse AC is given as x and the height of wall is opposite side of θ.

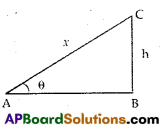
Thus, we consider sin θ to find the height.

Question 9.
Assertion : x + 2y – 30 = 0, 2x + 4y – 66 = 0 are inconsistent equations.
Reason: a₁x + b₁y + c₁ = 0, a₂x + b₂y + c₂ = 0 represent parallel lines if \(\frac{a_1}{a_2}\) = \(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) ≠ \(\frac{c_1}{c_2}\)
A) Both Assertion and Reason are true. Reason is supporting the Assertion
B) Both Assertion and Reason are true. Reason does not support the Assertion.
C) Assertion is true. Reason is False.
D) Assertion is False. Reason is True.
Solution:
(A) Both Assertion and Reason are true. Reason is supporting the Assertion.

Question 10.
If (p + 5)x³ + 2x² + 3x – 5 = 0 represents a quadratic equation, then find the value of p.
Solution:
5

Question 11.
If P(E) = 0.05, then P(not E) = ………..
Solution:
0.95.

Question 12.
The distance of the point (4, 7) from X – axis is ……….
Solution:
7 units.

Section – II
(8 × 2 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 2 marks.

Question 13.
How many bricks each measuring 25 cm × 11.25 m × 6 cm will be needed to build a wall 8 m × 6 m × 22.5 cm.
Solution:
Number of bricks \(=\frac{\text { Volume of the wall }}{\text { Volume of the brick }}\)
= \(\frac{800 \times 600 \times 22.5}{25 \times 11.25 \times 6}\) = 6400.

Question 14.
Two concentric circles of radii 5 cm and 3 cm are drawn. Find the length of the chord of larger circle which touches the smaller circle.
Solution:
As shown in the figure OP = 3 cm, OB = 5 cm
Since AB touches the smaller circle at P,
We have OP ⊥ AB ⇒ ∠OPB = 90°
∴ By Pythagoras theorem,
OB² = OP² + PB²
⇒ PB² = OB² – OP²
= 5² – 3² = 25 – 9
= 16
∴ PB = \(\sqrt{16}\) = 4 cm

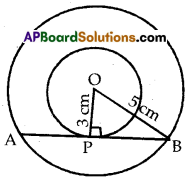
Since the perpendicular through the centre bisects a chord we have AP = PB = 4 cm
∴ AB = AP + PB
= 4 cm + 4 cm
= 8 cm
Thus, the length of the required chord = 8 cm.

Question 15.
If x = log₂3, y = log₂5 then write log₂15 in terms of x and y.
Solution:
log₂15 = log₂ (3 × 5)
= log₂3 + log₂5
= x + y
We know that log_a xy = log_ax + log_ay
Given log₂3 = x and log₂5 = y

Question 16.
Check whether the equations 2x + 3y = 1, 3x – y = 7 have a unique solution, infinitely many solutions
or no solution.
Solution:
2x + 3y = 1; 3x – y = 7
In the given equations \(\frac{a_1}{a_2}\) = \(\frac{2}{3}\)
\(\frac{\mathrm{b}_1}{\mathrm{~b}_2}\) = \(\frac{3}{-1}\) = -3
∴ \(\frac{a_1}{a_2}\) ≠ \(\frac{b_1}{b_2}\)
∴ The given system of equations has consistent and unique solution.

Question 17.
Find the arithmetic mean of the data 5, 6, 9, 10, 6, 6, 7.
Solution:
Arithmetic mean
= \(\frac{5+6+9+10+6+6+7}{7}\) = \(\frac{49}{7}\) = 7.

Question 18.
Two dice, one red and one yellow are thrown at the same time. Write down the possible out comes that the sum of the two numbers appearing on the top of the dice is 8.
Solution:
The possible out comes that the sum of the two numbers appearing on the top of the dice is 8 are given by
A ={(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}

Question 19.
Draw the venn diagram of A – B where A and B are non empty sets.
Solution:

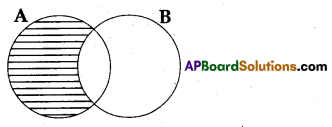
Question 20.
Find the value of ‘k’ for kx (x – 2) + 6 = 0 so that it has two equal roots.
Solution:
kx² – 2kx + 6 = 0
The given equation is in the form of
ax² + bx + c = 0 where a = k; b = -2k;
c = 6
Given that the quadratic equation has two equal roots.
∴ Discriminant = 0
b² – 4ac = 0
(-2k)² – 4(k)(6) = 0
4k² – 24k = 0
Divide the equation with ‘4k’
\(\frac{4 k^2}{4 k}\) – \(\frac{24 k}{4 k}\) = 0
k – 6 = 0
∴ k = 6

Section – III
(8 × 4 = 32 M)

Note:

1. Answer all the questions.
2. Each question carries 4 marks.

Question 21.
Find a quadratic polynomial with zeroes -2 and \(\frac{1}{3}\).
Solution:
Let the quadratic polynomial be ax² + bx + c, a ≠ 0 and its zeroes be α and β.
Here α = -2, β = \(\frac{1}{3}\)
Sum of the zeroes = (α + β)
= -2 + \(\left(\frac{1}{3}\right)\) = \(\frac{-5}{3}\)
Product of zeroes = (αβ)
= -2\(\left(\frac{1}{3}\right)\) = \(\frac{-2}{3}\)
Therefore the quadratic polynomial
ax² + bx + c is k [x² – (α + β)x + αβ],
where k is a constant = k[x² + \(\frac{5}{3}\)x – \(\frac{2}{3}\)]
We can put different values of k.
When k = 3, the quadratic polynomial will be 3x² + 5x – 2.

Question 22.
For what positive value of ‘p’, the following pair of linear equations have infinitely many solutions.
px + 3y – (p – 3) = 0; 12x + py – p = 0
Solution:
Given pair of equations are px + 3y – (p – 3) = 0 and 12x + py – p = 0
a₁ = p; b₁ = 3 ; c₁ = -(p – 3);
a₂ = 12; b₂ = p; c₂ = -p
Given equations has infinitely many solutions
∴ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)

Question 23.
Find a point on the Y-axis which is equidistant from both the points A (6, 5) and B (-4, 3).
Solution:
We know that a point on the Y – axis is of the form (0, y). So, let the point P (0, y) be equidistant from A and B. Then
PA = \(\sqrt{(6-0)^2+(5-y)^2}\)
PB = \(\sqrt{(-4-0)^2+(3-y)^2}\)
PA² = PB²
So, (6 – 0)² + (5 – y)² = (-4 – 0)² + (3 – y)²
i.e., 36 + 25 + y² – 10y = 16 + 9 + y² – 6y
i.e., 4y = 36
i.e., y = 9
So, the required point is (0, 9).
Let us check our solution :
AP = \(\sqrt{(6-0)^2+(5-9)^2}\)
So (0, 9) is equidistant from (6, 5) and (-4, 3).

Question 24.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Solution:
Given: ABCD is a rhombus whose diagonals AC and BD intersect at ‘O’.
AB = BC = CD = DA
To prove: AB² + BC² + CD² + DA² = AC² + BD²

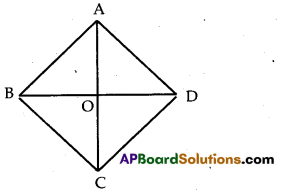
Proof:
The diagonals of a rhombus bisect perpendicularly each other.
⇒ AO = \(\frac{1}{2}\) AC and BO = \(\frac{1}{2}\) BD
Also ∆AOB is a right triangle.
∴ By Baudhayan theorem (Pythagoras theorem)
AB² = AO² + BO²
= \(\left(\frac{\mathrm{AC}}{2}\right)^2\) + \(\left(\frac{B D}{2}\right)^2\) = \(\frac{\mathrm{AC}^2}{4}\) + \(\frac{\mathrm{BD}^2}{4}\)
⇒ 4AB² = AC² + BD²
⇒ AB² + AB² + AB² + AB² = AC² + BD²
⇒ AB² + BC² + CD² + DA² = AC² + BD²
Hence the proof.

Question 25.
In figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm.
If OD = 2 cm., find the area of the shaded region.
(use π = \(\frac{22}{7}\))

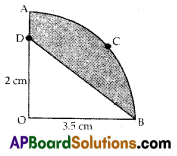
Solution:

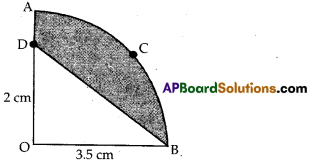
It is given that OACB is a quadrant of a circle with centre ‘O’.
⇒ ∠AOB = 90°
Radius = 3.5 cm and OD = 2 cm
Area of the sector shaped OACB = \(\frac{x^{\circ}}{360^{\circ}}\) × πr²
= \(\frac{90^{\circ}}{360^{\circ}}\) × \(\frac{22}{7}\) × 3.5 × 3.5 cm²
= \(\frac{1}{4}\) × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) cm²
= \(\frac{77}{8}\) cm² = 9.625 cm²
Area of ∆ODB = \(\frac{1}{2}\) × OB × OD
= \(\frac{1}{2}\) × 3.5 × 2 cm² = 3.5 cm²
∴ Area of shaded portion = Area of OACB – Area of ∆ODB
= 9.625 cm² – 3.5 cm²
= 6.125 cm²

Question 26.
Is it possible to design a rectangular park of perimeter 80m and area 400m². If so, find its length and breadth.
Solution:
Area of rectangular park = 400 m²
Let the length be x m.
The breadth = \(\frac{400}{x}\) m
Perimeter = 80 m
2(x + \(\frac{400}{x}\)) = 80
\(\frac{x^2+400}{x}\) = \(\frac{80}{2}\) = 40
x² + 400 = 40x
x² – 40x + 400 = 0
x² – 20x – 20x + 400 = 0
x(x – 20) – 20 (x – 20) = 0
(x – 20) (x – 20) = 0
x – 20 = 0; x – 20 = 0
x = 20; x = 20
The length of Park = 20m
breadth of park = \(\frac{400}{20}\) = 20m.

Question 27.
Which term of G.P. \(\sqrt{3}\), 3, 3\(\sqrt{3}\) …….. is 729 ?
Solution:

Question 28.
Draw diagram for the situation
“A person observes two banks of a river at angles of depression θ₁, and θ₂(θ₁ < θ₂) from the top of a tree of height “h” which is at a side of the river. The width of the river is “d”.
Solution:

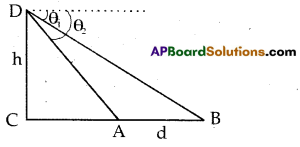
Section – IV
(5 x 8 = 40 M)

Note:

1. Answer all the questions.
2. Each question carries 8 marks.
3. Each question has internal choice.

Question 29.
a) If A = {x : x is a natural number)
B = {x : x is an even natural number)
C = {x : x is an odd natural number) and
D = {x : x is a prime number)
Find A – B, B∩C, A∪B, B – D
(OR)
b) The median of the following data is 525. Find the values of x and y, if the total frequency is 100. Here CI stands for class interval and Fr for frequency.

CI	0-100	100-200	200-300	300-400	400-500	500-600	600-700	700-800	800-900	900-1000
Fr	2	5	x	12	17	20	y	9	7	4

Solution:
A = {x : x is a natural number}
= {1, 2, 3, 4……..}
B = {x : x is an even natural number)
= {2, 4, 6, 8,…… }
C = {x : x is an odd natural number)
= {1, 3, 5, 7,……}
D = {x : x is a prime number)
= {2, 3, 5, 7,………}

i) A – B = {1, 2, 3, 4,…} – {2, 4, 6, 8,…}
= {1, 3, 5, ……..}
= {x : x is an odd natural number}

ii) B ∩ C = { } = φ

iii) A∪B = {1, 2, 3, 4,…..} ∪ {2, 4, 6, 8,…….}
= {1, 2, 3,……}
= A.

iv) B – D = {2, 4, 6, 8 } – {2, 3, 5, 7}
= {4, 6, 8,……..}

b)

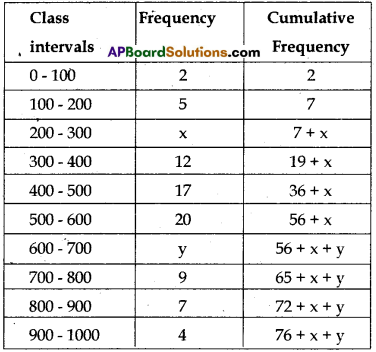
Given that, the total frequency,
n = 100
U.C. ⇒
2 + 5 + x + 12 + 17 + 20 + y + 9 + 7 + 4 = 100
⇒ x + y = 100 – 76 = 24 → (1)
\(\frac{n}{2}\) = 50
Median = 525 which is in the class 500 – 600.
So, l = 500, f = 20, cf = 2 + 5 + x + 12 + 17
= x + 36, h = 100
So, 525 = l + \(\frac{\left(\frac{n}{2}-c f\right)}{f}\) × h
⇒ 525 = 500 + \(\left[\frac{50-(x+36)}{20}\right]\) × 100
⇒ 525 = 500 + 5 (-x + 14)
⇒ 5 (-x + 14) = 25 ⇒ -x + 14 = 5
⇒ x = 9 → (2)
Put (2) in (1), 9 + y = 24 ⇒ y = 15
So, required values are x = 9 and y = 15.

Question 30.
a) Find the value of K for the points (7, -2), (5,1) and (3, K) are collinear.
(OR)
b) A sphere, a cylinder and a cone are of the same radius and same height. Find the ratio of their curved surface areas.
Solution:
a) Given points (7, -2), (5, 1), (3, K)
Here x₁ = 7, y₁ = -2, x₂ = 5, y₂ = 1, x₃ = 3, y₃ = K
Area of triangle

(OR)

b) Let r be the common radius of a sphere, a cone and cylinder
Curved surface area of sphere = 4 πr²
Height of sphere = diameter = 2r
Height of the cone = height of cylinder
= height of sphere = 2r
Curved surface area of cylinder = 2 πrh
= 2π.r. (2r) = 4 πr²

Curved surface area of sphere = 4πr²
Curved surface area of cylinder
= 2πrh = 2πr × 2r = 4πr²
Ratio of curved surface area of sphere,
cylinder and cone = 4πr² : 4πr² : \(\sqrt{5}\)πr² = 4 : 4 : \(\sqrt{5}\).

Question 31.
a) Prove that \(\sqrt{2}\) + \(\sqrt{3}\) is irrational.
(OR)
b) If cosecθ + cotθ = k then prove that cos θ = \(\frac{\mathrm{k}^2-1}{\mathrm{k}^2+1}\).
Solution:
a) Let us suppose that \(\sqrt{2}\) + \(\sqrt{3}\) is rational.
Let \(\sqrt{2}\) + \(\sqrt{3}\) = \(\frac{\mathrm{a}}{\mathrm{b}}\), where a, b are integers and b ≠ 0
Therefore,
Squaring on both sides, we get

Since, a, b are integers, \(\frac{a^2+b^2}{2 a b}\) is rational, and so, \(\sqrt{3}\) is rational.
This contradicts the fact that \(\sqrt{3}\) is irrational. Hence, \(\sqrt{2}\) + \(\sqrt{3}\) is irrational.

(OR)

b) Suppose cosecθ + cotθ = k …….. (1)
we have, cosec²θ – cot²θ = 1
⇒ (cosecθ + cotθ) (cosecθ – cotθ) = 1
⇒ k(cosecθ – cotθ) = 1.
⇒ (cosecθ – cotθ) = \(\frac{1}{\mathrm{k}}\) ……… (2)
Adding (1) and (2) we get
cosecθ + cotθ + cosecθ – cotθ = k + \(\frac{1}{\mathrm{k}}\)
⇒ 2 cosecθ = k + \(\frac{1}{\mathrm{k}}\) ……. (3)
Subtracting (1) and (2) we get
cosecθ + cotθ – cosecθ + cotθ = k – \(\frac{1}{k}\)
⇒ 2 cotθ = k – \(\frac{1}{\mathrm{k}}\) ……. (4)
From (3) and (4), we have

Question 32.
a) 200 logs are stacked in the following manner : 20 logs in the bottom row, 19 in the next row, 18 in the
row next to it and so on. In how many rows are the 200 logs placed and how many logs are in the top row?
(OR)
b) A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
i) a two-digit number
ii) a perfect square.
Solution:
a) Number of logs in each row 20, 19, 18, 17, …., is an AP.
Total number of logs = 200
a = 20; d = 19 – 20 = – 1, S_n = 200
s_n = [2a + (n – 1)d]
200 = \(\frac{n}{2}\) [2 × 20 + (n – 1)(-1)]
n(40 – n + 1) = 400
n(41 – n) = 400
41n – n² = 400
n² – 41n + 400 = 0
By applying factorization method,
n² – 25n – 16n + 400 = 0
n(n – 25) – 16(n – 25) = 0
(n – 25) (n – 16) = 0
Either (n – 25) or (n – 16) = 0
n – 25 = 0 gives n = 25
n – 16 = 0 gives n = 16
Number of rows = 16
S_n = \(\frac{n}{2}\) (a + l)
Here a = 20 ; n = 16 ; S_n = 200 ; l = ?
200 = \(\frac{16}{2}\)(20+l)
8(20+l) = \(\frac{200}{8}\)
20 + l = 25
l = 25 – 20 = 5
\(\frac{25}{2}\)(20 + l) = 200
500 + 25l = 400
25l = 400 – 500 = 100
l = \(\frac{-100}{25}\) = -4
l can’t in negative
∴ 25 is not no. of rows
∴ no. of rows = 16
no. of logs in the top row = 5

(OR)

b) In the given experiment, sample space S
= {1, 2, ………., 90}
n(S) = 90

i) Let A denote the event that the drawn disc bears a two – digit number. Then, A = {10, 11, ………,90} Number of two digit numbers ‘n’ (A) = 81
So, required probability P(A)
= \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{81}{90}\) = \(\frac{9}{10}\)

ii) Let B denote the event that the drawn disc bears a perfect square number.
Then, B = {1, 4, 9,16, 25, 36, 49, 64, 81}
n(B) = 9
So, required probability P(B) = \(\frac{n(B)}{n(S)}\)
= \(\frac{9}{90}\) = \(\frac{1}{10}\)

Question 33.
a) Draw the graph of x² – 6x + 9 and find the zeroes.
(OR)
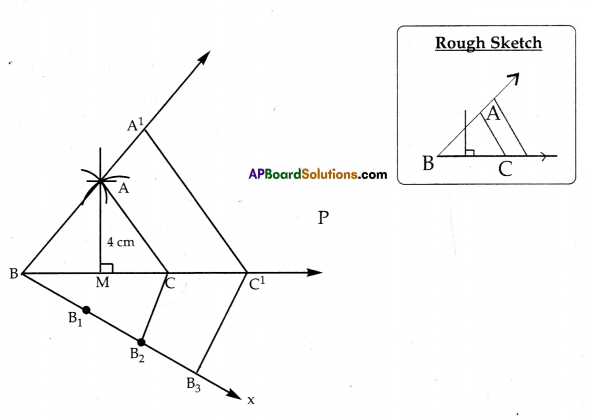
b) Construct an Isosceles triangle whose base is 8cm and altitude is 4 cm. Then, draw another triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of the isosceles triangle.
Solution:
p(x) = x² – 6x + 9
y = x² – 6x + 9

x	-1	0	1	2	3	4	5
y = x2 – 6x + 9	16	9	4	1	0	1	4
(x, y)	(-1, 16)	(0, 9)	(1, 4)	(2, 1)	(3, 0)	(4, 1)	(5, 4)

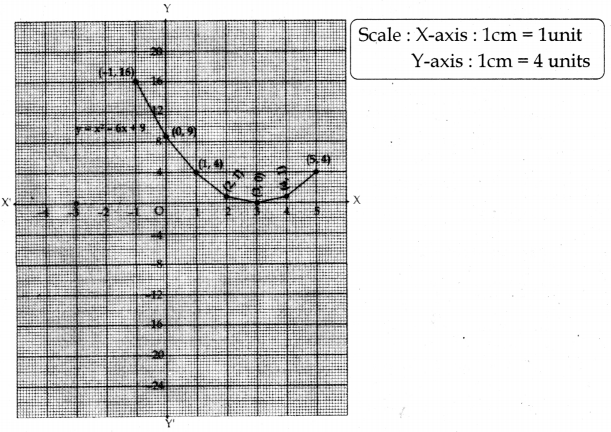
3 is a zero of the quadratic polynomial because (3, 0) is intersection point of X axis.
Justification: x² – 6x + 9 = 0
x² – 2. x. 3 + 3² = 0
(x – 3)² = 0
x = 3
∴ zeroes of p (x) = 3.

(OR)

b) Steps of construction :

1. Construct an isosceles triangle ABC with the given measurements.
2. Draw a ray BX making an acute angle with BC on the opposite side of A.
3. Locate 3 points B₁, B₂, B₃ on BX so that BB₁ = B₁B₂ = B₂B₃.
4. Produce BC upto P
5. Join B₂C and draw a line from B₃ to C¹ which is parallel to B₂C and it is intersecting BP at C¹.
6. Draw a line through C¹ parallel to CA to intersect the produced line of BA at A¹
   ∴ A’BC’ is the required triangle.