AP 10th Class Maths Question Paper July 2022 with Solutions

Regularly solving AP 10th Class Maths Model Papers and AP 10th Class Maths Question Paper July 2022 contributes to the development of problem-solving skills.

AP SSC Maths Question Paper July 2022 with Solutions

Time : 3.15 hours
Max. Marks : 100

Instructions:

1. In the duration of 3 hours 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the answer booklet only.
3. Question paper consists of 4 Sections and 33 questions.
4. Internal choice is available in section – IV only.
5. Answers shall be written neatly and legibly.

Section – I
(12 × 1 = 12 M)

Note :

1. Answer all the questions in one word or phrase.
2. Each question carries 1 mark.

Question 1.
Express 0.75 in p/q form.
Solution:
\(\frac{75}{100}\) or \(\frac{3}{4}\)

Question 2.
Match the following :

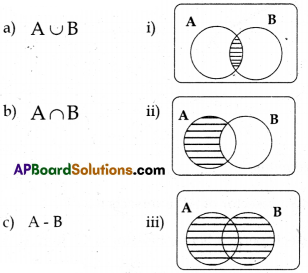
Choose the correct answer.
A) a-ii, b-iii, c-i
B) a-iii, b-i, c-ii
C) a-i, b-ii, c-iii
D) a-iii, b-ii, c-i
Solution:
B) a-iii, b-i, c-ii

Question 3.
Number of zeroes of cubic polynomial …………
Solution:
at most 3

Question 4.
As shown in the figure, a hemisphere is placed on a cone. How do you find the surface area of the figure?

Solution:
S.A of figure = C.S.A of hemisphere + C.S.A of cone.

Question 5.
Express 2y = 5x + 7 in the form of ax + by + c = 0
Solution:
5x – 2y + 7 = 0

Question 6.
Identify the distance between A (8, 3) and B (4, 3) from the following.
A) 12
B) 0
C) 4
D) 6
Solution:
C) 4

Question 7.
Statement ‘p’ : A tangent to a circle intersects it in one point.
Statement ‘q’: We can draw infinite tangents to a given circle.
A) Statement ‘p’ and ‘q’ both are true
B) Statement ‘p’ true ‘q’ is false
C) Statement ‘p’ false ‘q’ both are true
D) Statement ‘p’ and q’ both are false
Solution:
A) Statement ‘p’ and ‘q’ both are true

Question 8.
Write the relation between Cosθ and Secθ
Solution:
cosθ = \(\frac{1}{\sec \theta}\) or secθ = \(\frac{1}{\cos \theta}\) or sec θ . cos θ = 1

Question 9.
Identify the angle of depression from the given figure.

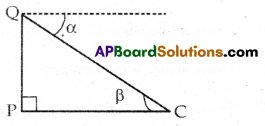
Solution:
α

Question 10.
From the given frequency distribution table, what is the class interval of highest frequency class?

Class interval	1-3	3-5	5-7	7-9	9-11
Frequency	7	8	2	2	1

Solution:
3 – 5

Question 11.
If P(E) = 0.4, then what is the probability of ‘not E’?
Solution:
0.6

Question 12.
“In a right triangle, the square of hypotenuse is equal to the sum of the squares of the other two sides. ‘The above theorem is related to which Mathematician?
A) Baudhavan
B) Aryabhata
C) Euclid
D) Bhaskaracharva
Solution:
A) Baudhavan

Section – II
(8 × 2 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 2 marks.

Question 13.
Find the H.C.F. of 12, 15 and 21
Solution:
Given numbers are 12, 15, 21 12
12 = 2² × 3
15 = 5 × 3
21 = 7 × 3
HCF of 12, 15 and 21 is 3.

Question 14.
If p(t) = t³ – 1, then find the values of p(1) and p(0). Identify the zero value.
Solution:
p(t) = t³ – 1
p(1) = 1³ – 1 = 1 – 1 = 0
p(0) = 0³ – 1 = 0 – 1 = -1
Zero of the given polynomial is 1.

Question 15.
If 3x + 4y = 2 and px + 8y = 4 equations represent two coincident lines, then find the value of ‘p’.
Solution:
Given 3x + 4y = 2 and px + 8y = 4 are coincident lines
Here a₁ = 3, b₁ = 4, c₁ = -2
a₂ = p, b₂ = 8, c₂ = -4
Since lines are coincident b,
\(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)
⇒ \(\frac{3}{\mathrm{p}}\) = \(\frac{4}{8}\) = \(\frac{2}{4}\)
⇒ p = \(\frac{8 \times 3}{4}\) = 6

Question 16.
Find the mid point of the line segment joining the points (3, 0) and (-1, 4).
Solution:
Given points are (x₁, y₁) = (3, 0) and (x₂, y₂) = (-1, 4) Mid point of the line segment joining the given points is

Question 17.
Find the volume of right circular cone with radius 6 cm, and height 7 cm.
Solution:
Radius of the cone (r) = 6 cm
Height (h) = 7 cm
Volume(v) = \(\frac{1}{3}\)πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7} \frac{22}{7} \frac{22}{7}\) × 6 × 6 × 7 cm³
Volume of cone = 264 cm³

Question 18.
Prove that the tangents to a circle at the end points of a diameter are parallel.
Solution:
Let O’ be the centre of circle, AB is diameter.
PQ and RS are two tangents of the circle at contact points A and B respectively.

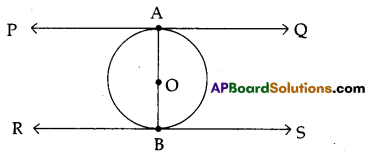
We have to prove that PQ//RS
Since PQ is tangent
OA ⊥ PQ (∵ Tangent at any point of the circle is perpendicular to the radius through point of contact)
= AB ⊥ PQ
Similarly AB ⊥ RS
We know that two lines perpendicular to a same line are parallel.
∴ PQ || RS.
Hence proved.

Question 19.
Jani observes Vanaja on the ground from the ‘ balcony of the first floor of a building at an angle of depression 60°. The height of the first floor of the building is 10 meters. Draw the diagram for this data.
Solution:

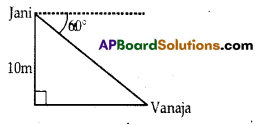
Question 20.
If the mean of 8, 11, 13, x, 9 and 3 is 8, find the value of x.
Solution:
Given numbers are 8, 11, 13, x, 9 and 3
Mean of the numbers is 8
Mean = \(\frac{\sum x_i}{N}\)
8 = \(\frac{8+11+13+x+9+3}{6}\)
⇒ 44 + x = 6 × 8
⇒ x = 48 – 44 = 4
∴ x = 4

Section – III
(8 × 4 = 32 M)

Note:

1. Answer all the questions.
2. Each question carries 4 marks.

Question 21.
If A = {2, 5, 6, 8) and B = {1, 5, 7, 9}, find
(i) A ∪ B and
(ii) A – B and draw Venn diagram.
Solution:
A = {2, 5, 6, 8}
B = {1, 5, 7, 9}

i) A∪B = {2, 5, 6, 8} ∪ {1, 5, 7, 9}
= {1, 2, 5, 6, 7, 8, 9}

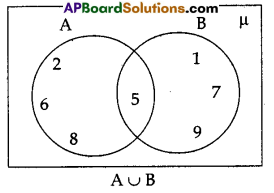
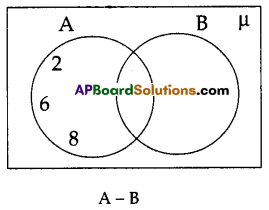
ii) A – B = {2, 5, 6, 8} – {1, 5, 7, 9}
= {2, 6, 8}

Question 22.
Check whether, ‘-150’ is a term of an A.P. : 11, 8, 5, 2, ……….
Solution:
Given A.P. : 11, 8, 5, 2 ………
a₁ = 11
d = a₂ – a₁
= 8 – 11
= -3
a_n = a₁ + (n – 1)d
⇒ 11 + (n – 1)(-3) = -150 – 11
⇒ (n – 1)(-3) = -150 – 11
⇒ (n – 1) (-3) = -161
⇒ n – 1 = \(\frac{161}{3}\)
⇒ n = \(\frac{161}{3}\) = 1 + \(\frac{164}{3}\)
Since ‘n’ is not a positive integer, -150 is not a term of given A.P

Question 23.
Solve the pair of equations by reducing them to a pair of linear equations.
\(\frac{2}{\sqrt{x}}\) + \(\frac{3}{\sqrt{y}}\) = 2 ; \(\frac{4}{\sqrt{x}}\) – \(\frac{9}{\sqrt{y}}\) = -1
Solution:
\(2\left(\frac{1}{\sqrt{x}}\right)\) + \(3\left(\frac{1}{\sqrt{y}}\right)\) = 2 …….. (1)
\(4\left(\frac{1}{\sqrt{x}}\right)\) – \(9\left(\frac{1}{\sqrt{y}}\right)\) = -1 …….. (2)
If we substitute \(\frac{1}{\sqrt{x}}\) = p and \(\frac{1}{\sqrt{y}}\) = q
we get a pair of linear equations.
2p + 3q = 2 ……… (3)
4p – 9q = -1 ……. (4)
Elimination Method:

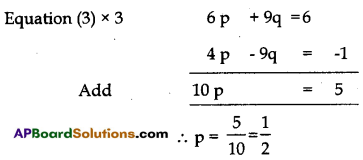
Substitute the value of p in equation (4)

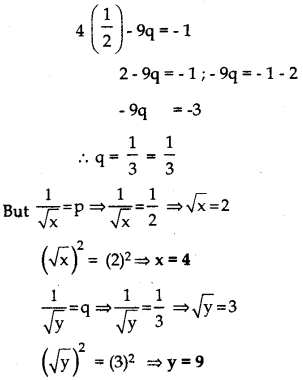
Question 24.
Two poles of heights 6 m and 11 m stands on a plane ground. 1f the distance between the feet of the poles is 12 m, then find the distance between their tops.
Solution:
Length of pole AB = 6 m
Length of pole CD = 11 m
Distance between the feet of two poles
= 12 m
By Drawing AE ⊥ CD
ABCE is a rectangle
∴ AB = CE = 6.m
BC = AE = 12 m
CD = CE + ED
11 = 6 + ED

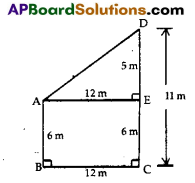
⇒ ED = 11 – 6 = 5 m
In right angled traingle AED,
AD² = AE² + ED²
(By Pythagoras theorem)
AD² = 12² + 5²
AD = \(\sqrt{144+25}\)
AD = \(\sqrt{169}\) = 13 m
Distance between the tops of poles is 13 m

Question 25.
If A, B and C are interior angles of a triangle ABC, then show that sin\(\left(\frac{B+C}{2}\right)\) = cos\(\frac{A}{2}\)
Solution:
Given A, B, C are interior angles of ∆ ABC

Question 26.
Suppose Siddu is shooting an arrow from the top of a building at an height of 6 m to a target on the ground at an angle of depression of 60°. What is the distance between Siddu and the object ?
Solution:
Height of the building AB = 6 m
Angle of depression = 60°

Question 27.
A box contains 3 blue, 2 white and 4 red marbles. If a marble is drawn at random from die box, what is the probability that it will be
(i) white
(ii) red ?
Solution:
Given 3 blue, 2 white, 4 red marbles are in the box
Total number of outcomes in sample space n(S) = 3 + 2 + 4 = 9

i) Number of favourable outcomes for getting white marble n(E₁) = 2
Probability of getting white marble
P(E₁) = \(\frac{n\left(E_1\right)}{n(S)}\) = \(\frac{2}{9}\)

ii) Number of favourable outcomes for getting
red marble n(E₂) = 4
Probability of getting red marble
P(E₂) = \(\frac{n\left(E_2\right)}{n(S)}\) = \(\frac{4}{9}\)

Question 28.
Find the dimensions of a rectangle whose perimeter is 28 meters and whose area is 40 square meters.
Solution:
Area of rectangle = 40 sq.m.
Let the length of rectangle be = x m.
x × breadth = 40
breadth = \(\frac{40}{x}\)m
Perimeter of rectangle = 28 m
2(l + b) = 28
2(x + \(\frac{40}{x}\) = 28
\(\frac{x^2+40}{x}\) = \(\frac{28}{2}\) = 14
x² + 40 = 14x
x² – 14x + 40 = 0
x² – 10x – 4x + 40 = 0
x(x – 10) -4(x – 10) = 0
(x – 10)(x – 4) = 0
x – 10 (or) x – 4 = 0
x = 10 (or) x = 4
If length = 10 m then breadth = \(\frac{40}{10}\) = 4 m
If length = 4 m then breadth
= \(\frac{40}{4}\) = 10 m
∴ dimensions of rectangle = 10 m, 4 m

SECTION – IV
(5 × 8 = 40 M)

Note:

1. Answer all the questions.
2. Each question carries 8 marks,
3. Each question has internal choice.

Question 29.
a) Show that 5 – \(\sqrt{3}\) is irrdtional
(OR)
b) Prove that

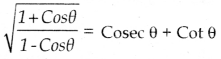
Solution:
a)
Let us assume that 5 – \(\sqrt{3}\) is rational.
That is, we can find coprimes ‘a’ and ‘b’ (b ≠ 0) such that
5 – \(\sqrt{3}\) = \(\frac{\mathrm{a}}{\mathrm{b}}\) ∴ 5 – \(\frac{\mathrm{a}}{\mathrm{b}}\) = \(\sqrt{3}\)
Rearranging this equation we get
∴ \(\sqrt{3}\) = 5 – \(\frac{\mathrm{a}}{\mathrm{b}}\) = \(\frac{5 b-a}{b}\) ……. (1)
Since ‘a’ and ‘b’ are integers, the RHS of equation (1) \(\frac{5 b-a}{b}\) is rational.
So the LHS \(\sqrt{3}\) also rational.
But this contradicts the fact that \(\sqrt{3}\) is irrational.
This contradiction has arisen because of our incorrect assumption that 5 – \(\sqrt{3}\) is rational.
So, we conclude that 5 – \(\sqrt{3}\) is irrational.

(OR)

b) L.H.S = \(\sqrt{\frac{1+\cos \theta}{1-\cos \theta}}\)
By rationalising, we get

Question 30.
a) If A = {3, 6, 9, 12, 15, 18, 21}, B = {4, 8, 12, 16, 20}, C = {2, 4, 6, 8, 10, 12, 14, 16}, then find the following:
i) A – B
ii) A – C
iii) B – C
iv)B∪C
(OR)
b) Find the 12^th term of a G.P. whose 8th term is 192 and the common ratio is 2.
Solution:
a)
Given A = {3, 6, 9, 12, 15, 18, 21};
B = {4, 8, 12, 16, 20}
C = {2, 4, 6, 8, 10, 12, 14, 16}
i) A – B = {3, 6, 9, 12, 15, 18, 21} – {4, 8, 12, 16, 20}
= {3, 6, 9, 15, 18, 21}

ii) A – C = {3, 6, 9, 12, 15, 18, 21} – {2, 4, 6, 8, 10, 12, 14, 16}
= {3, 9, 15, 18, 21}

iii) B – C = {4, 8, 12, 16, 20} – {2, 4, 6, 8, 10, 12, 14, 16}
= {20}

iv) B∪C = {4, 8, 12, 16, 20} ∪ {2, 4, 6, 8, 10, 12, 14, 16}
= {4, 8, 12, 16, 20, 2, 6, 10, 14}
= {2, 4, 6, 8, 10, 12, 14, 16, 20}

(OR)

b) Let the first term of the G.P be a and common ratio r = 2
Also given 8^th term of the GP is 192.
∴ ar⁷ = 192
⇒ a . 2⁷ = 192
⇒ a = \(\frac{192}{128}\) = \(\frac{3}{2}\)
12th term of the GP is ar¹¹
= \(\frac{3}{2}\)(2)¹¹ = 3(2¹⁰)
= 3072

Question 31.
a) Prove that the points A (7, 3), B (6, 1), C(8, 2) and D (9, 4) taken in order are the corners of a parallelogram.
(OR)
b) The following data gives the information on the observed life times (in hours) of 225 electrical components

Life time (in hours)	0-20	20-40	40-60	60-80	80-100	100-120
Frequency	10	35	52	61	38	29

Determine the modal life times of the components.
Solution:
Let the points
A(7, 3), B(6, 1), C(8, 2) and D(9, 4) are given verticles.

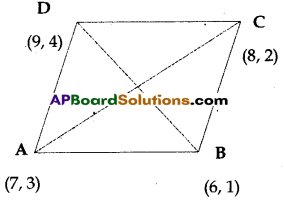
We know that the diagonals of a parallelogram bisect each other.
∴ So the midpoints of the diagonals AC and DB should be equal.
Now, we find the mid points of AC and DB by using the formula
\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
Mid point of AC
= \(\left(\frac{7+8}{2}, \frac{3+2}{2}\right)\) = \(\left(\frac{15}{2}, \frac{5}{2}\right)\)
Hence, mid point of AC = Mid point of DB
∴ The points A, B, C, D taken in order are the vertices of a a parallelogram.

(OR)

b)

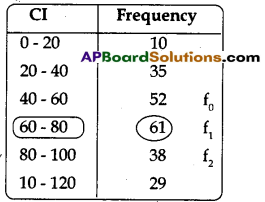
Since, the maximum frequency is in the interval 60 – 80, the modal class is 60 – 80.
We have,
Mode = l + \(\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right)\) × h
Here, l = 60
f₀ = 52
f₁ = 61
f₂ = 38
h = 20
Mode = 60 + \(\left(\frac{61-52}{2(61)-52-38}\right)\) × 20
= 60 + \(\frac{9}{32}\) × 20
= 60 + \(\frac{90}{16}\) = 60 + 5.625
= 65.625 hrs.

Question 32.
a) A sphere, a cylinder and a cone are of the same radius and same height. Find the ratio of their curved
surface areas.
(OR)
b) One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting :
i) A face card of diamond;
ii) Ace card;
iii) Spade card;
iv) A jack of red’
Solution:
a) Let r be the common radius of a sphere, a cone and cylinder
Curved surface area of sphere = 4πr²
Height of sphere diameter = 2r
Height of the cone = height of cylinder
= height of sphere
= 2r
Curved surface area of cylinder = 2 πrh
= 2 π.r.(2r) = 4 πr²
Slant height of cone (l)
= \(\sqrt{\mathrm{r}^2+\mathrm{h}^2}\)
= \(\sqrt{r^2+(2 r)^2}\)
= \(\sqrt{r^2+4 r^2}\)
= \(\sqrt{5 r^2}\) = \(\sqrt{5 r}\)
Curved surface area of the cone
= π r l
= π. r. \(\sqrt{5}\) . r
= \(\sqrt{5}\) πr²
Curved surface area of sphere
= 4 π r²
Curved surface area of cylinder
= 2 π rh = 2 π r × 2 r
= 4 π r²
Ratio of curved surface area of sphere, cylinder and cone
= 4πr² : 4πr² : \(\sqrt{5}\)πr².
= 4 : 4 : \(\sqrt{5}\)

(OR)

b) Number of cards in the deck n (S) = 52
i) Number of favourable outcomes to get a face card of diamond n (E₁) = 3
Probability of getting a face card of diamond P(E₁) = \(\frac{\mathrm{n}\left(\mathrm{E}_1\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{52}\)

ii) Number of favourable outcomes to get an Ace n (E₂) = 4
Probability of getting an Ace P (E₂) = \(\frac{\mathrm{n}\left(\mathrm{E}_2\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{4}{52}\) = \(\frac{1}{13}\)

iii) Number of favourable outcomes to get a spade card n(E₃) = 13
Probability of getting a spade card P(E₃) = \(\frac{\mathrm{n}\left(\mathrm{E}_3\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{13}{52}\) = \(\frac{1}{4}\)

iv) Number of favourable outcomes to get a jack of red n(E₄) = 2
Probability of getting a jack card of red P (E₄) = \(\frac{\mathrm{n}\left(\mathrm{E}_4\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{2}{52}\) = \(\frac{1}{26}\)

Question 33.
a) Draw the graph of the given polynomial p(x) = x² – 6x + 9 and find the zeroes.
(OR)
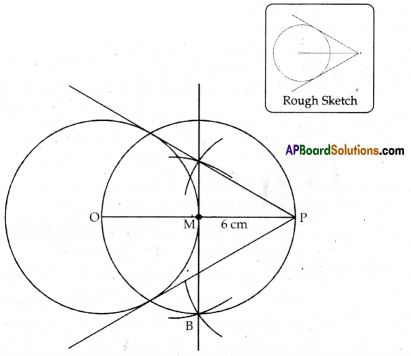
b) Draw a circle of radius 4 cm. From a point 6 cm away from its center, construct the pair of tangents to the circle.
Solution:
a) p(x) = x² – 6x + 9; y = x² – 6x + 9

x	-1	0	1	2	3	4	5
y = x2 – 6x + 9	16	9	4	1	0	1	4
(x, y)	(-1,16)	(0,9)	(1,4)	(2,1)	(3,0)	(4,1)	(5, 4)

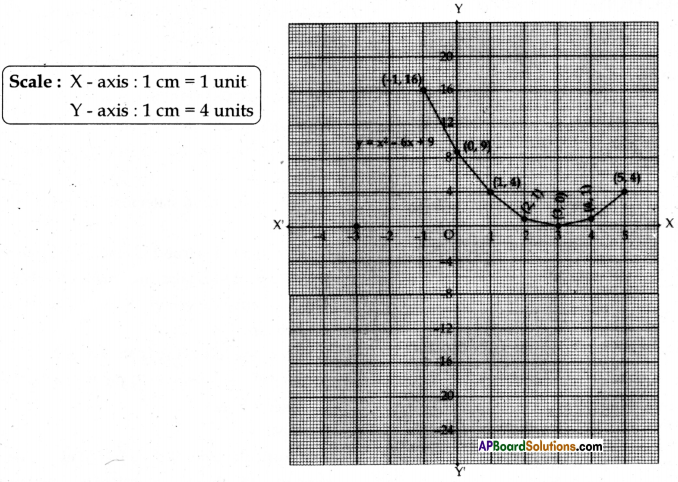
(OR)

b)
Draw a circle of radius 4 cm with centre ‘O’.
Plot a point P, such that OP = 6 cm
Bisect OP at M and for drawing a circle with radius OM or MP
Draw tangents from P to the intersecting points of two circles.