AP 10th Class Maths Model Paper 2023 with Solutions

Regularly solving AP 10th Class Maths Model Papers and AP 10th Class Maths Board Model Paper 2023 contributes to the development of problem-solving skills.

AP SSC Maths Model Paper 2023 with Solutions

Time : 3.15 hours
Max. Marks : 100

Instructions:

1. In the duration of 3 hours 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the answer booklet only.
3. Question paper consists of 4 Sections which includes 33 questions.
4. Internal choice is available in section – IV only.
5. Answers shall be written neatly and legibly.

Section – I
(12 × 1 = 12 M)

Note:

1. Answer all the questions in one word or phrase.
2. Each question carries 1 mark.

Question 1.
“The cost of 2 pens and 5 pencils is Rs. 20”. Express this data as a linear equation.
Solution:
Let the pens = X and pencils = y
The cost of 2 pens and 5 pencils = ₹ 20.
∴ 2x + 5y = 20

Question 2.
Choose the correct answer satisfying the following statements.
Statement (A) : Number of maximum zeroes of a cubic polynomial is 3.
Statement (B) : Zero of a linear polynomial x – 2 is -2.
i) Both (A) and (B) are TRUE.
ii) (A) is TRUE, (B) is FALSE
iii) (A) is FALSE, (B) is TRUE,
iv) Both (A) and (B) are FALSE.
Solution:
(ii) [A is TRUE, B is FALSE]

Question 3.
Find the value of Log₆36.
Solution:
Let log₆36 = x
6^x = 36
6^x = 6²
x = 2
∴ log₆36 = 2

Question 4.
Find the discriminant of quadratic equation x² – 5x + 6 = 0.
Solution:
x² – 5x + 6 = 0
where a = 1, b = -5, c = 6.
discriminant = b² – 4ac
= (-5)² – 4 × 1 × 6
= 25 – 24
= 1

Question 5.
Find the volume of a cylinder whose base radius is 3 cm and height is 7 cm.
Solution:
Base radius of a cylinder = r = 3 cm
height = h = 7 cm
Volume of a cylinder = πr²h
= \(\frac{22}{7}\) × 3² × 7
= 22 × 9
= 198 cm³

Question 6.
If n(A) = 10, n(B) = 6 and n(A∪B) = 12, then n(A∩B) = ………….
Solution:
n(A) = 10, n(B) = 6, and n(A∪B) = 12, n(A∩B) = ?
n(A∪B) = n(A) + n(B) – n(A∩B)
12 = 10 + 6 – n(A∩B)
n(A∩B) = 16 – 12
n(A∩B) = 4

Question 7.
Given two examples of pair of similar figures.
Solution:
i) A pair of circles are similar
ii) A pair of square are similar

Question 8.
Match the following:

a) A → (i), B → (ii), C → (iii)
b) A → (ii), B → (iii), C → (i)
c) A → (iii), B → (i), C → (ii)
d) A → (ii), B → (i), C → (iii)
Solution:
c) A→(iii), B→(i), C→(ii)]

Question 9.
Midpoint of a line joining the two points (0, 0) and (4, 6) is ………..
Solution:
The midpoint of a line joining the two points (0, 0) and (4, 6) is
= \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
= \(\left(\frac{0+4}{2}, \frac{0+6}{2}\right)\) = \(\left(\frac{4}{2}, \frac{6}{2}\right)\) = (2, 3)

Question 10.
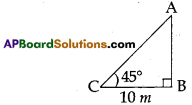
Draw a rough diagram to the given situation.
“A person observed a top of a tree 10 m away from its foot at the angle of elevation is 45°.”
Solution:
Height of the tree = AB
The distance of a person from foot of the tree = BC = 10 m
Angle of elevation = ∠BCA = 45°

Question 11.
Assertion : Mode of sin 0°, cos 0°, sin 90° and tan 45″ is 0
Reason : \(\bar{x}\) = \(\frac{\sum f_i x_i}{\sum f}\)
Choose the correct answer
A) Both Assertion and Reason are true. Reason is supporting the Assertion.
B) Both Assertion and Reason are true. But Reason is not supporting the Assertion.
C) Assertion is true but the Reason is false.
D) Assertion is false but the Reason is true.
Answer:
D) Assertion is false and Reason is true

Question 12.
The number of common tangents can be drawn to two concentric circles is ……..
Answer:
0

Section – II
(8 × 2 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 2 marks.

Question 13.
If x + 2y = 7 and 4x – ay = 10 has no solution, then find the value of ‘a’.
Solution:
x + 2y = 7 and 4x – ay = 10
a₁ = 1; b₁ = 2; c₁ = 7
a₂ = 4; b₂ = -a; c₂ = 10
Given pair of linear equations has no solution.
So they are parallel lines
∴ \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\)
\(\frac{1}{4}\) = \(\frac{2}{-a}\) ≠ \(\frac{7}{10}\)
\(\frac{1}{4}\) = \(\frac{2}{-a}\) = -a = 2 × 4
-a = 8
a = -8

Question 14.
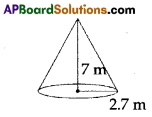
In a construction of kitchen shed at school, a truck unloaded the sand which was formed in the shape of a cone. The base radius of the cone is 2.7 m. and its height is 7 m. Find the volume of sand unloaded there.
Solution:
The unloaded sand was formed in the shape of a cone.
The base radius of cone = r = 2.7 m
height = h = 7 m

∴ The volume of sand = volume of cone

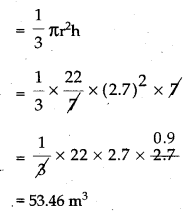
Question 15.
Express the following sets in set-builder form :
i) A = {1, 8, 27, 64}
ii) B = {-3, -2, -1, 0, 1, 2}
Solution:
i) A = {1, 8, 27,64}
= {1³, 2³, 3³, 4³}
= [x : x = n³, n ∈ N and n ≤ 4}

ii) B = {-3, -2, -1, 0, 1, 2}
= {x : x ∈ Z and -3 < x < 2}

Question 16.
Find the HCF of 220 and 40 by using Euclid Division Lemma.
Solution:
When 220 is divided by 40
220 = 40 × 5 + 20
40 = 20 × 2 + 0
∴ The H.C.F. of (220, 40) is 20.

Question 17.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other is a secant to the circle.
Solution:

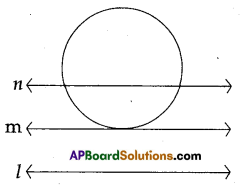
In the figure l is a given line and l || m || n such that m is a tangent and n is secant of the circle.

Question 18.
If tanθ = \(\frac{7}{24}\), then find the value of sec θ.
Solution:
tan θ = \(\frac{7}{24}\)
sec²θ – tan²θ = 1
sec²θ = 1 + tan²θ
= 1 + \(\left(\frac{7}{24}\right)^2\)
= 1 + \(\frac{49}{576}\)
= \(\frac{576+49}{576}\) = \(\frac{625}{576}\)
secθ = \(\sqrt{\frac{625}{576}}\) = \(\frac{25}{24}\)

Question 19.
Write the formula to find mean of grouped data in direct method and explain the terms in it.
Solution:
Mean of grouped data by direct method
\((\bar{x})\) = \(\frac{\sum f_i x_i}{\sum f_i}\)
f_i = Frequency of corresponding class
x_i = Mid value (class mark)
Σf_i = Total frequency

Question 20.
Show that the centroid of a triangle formed by the vertices (o, o), (2, 0) and (1, 3) is (1, 1).
Solution:
Centroid of a triangle formed by the vertices (0, 0), (2, 0), and (1,3) is

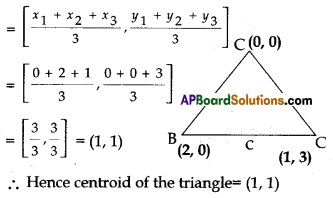
Section – III
(8 × 4 = 32)

Note:

1. Answer all the questions.
2. Each question carries 4 marks.

Question 21.
‘Find the zeroes of the polynomial x² + 7x + 10 and verify the relation between the co-efficients of the polynomial and the zeroes of the polynomial
Solution:
We have
x² + 7x + 10 = (x + 2) (x + 5)
So, the value of x² + 7x + 10 is zero when x + 2 = 0 or x + 5 = 0,
i.e., when x = -2 or x = -5.
Therefore, the zeroes of x² + 7x + 10 are -2 and -5.
Now, sum of the zeroes= -2 + (-5) = – (7)
= \(\frac{-(7)}{1}\) = \(\frac{-(\text { coefficient of } x)}{\text { coefficient of } x^2}\)
Product of the zeroes = -2 × (-5) = 10
= \(\frac{10}{1}\) = \(=\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)

Question 22.
Kavitha went to a bank to withdraw Rs. 8,000. She asked the cashier to give the cash in Rs. 100 and Rs. 500 notes only. She got 32 notes in all. Can you tell how many notes each of Rs. 100 and Rs. 500 she received?
Solution:
Let the number of ₹ 100 notes be x
Let the number of ₹ 500 notes be y
She got 32 notes in all
∴ x + y = 32 → 1
The amount of money withdraw = ₹ 8000
100 x + 500 y = 8000 → (2)
From eq(1) y = 32 – x
y = 32 – x is subsituting in eq(2)
100x + 500(32 – x) = 8000
100x + 16000 – 500x = 8000
-400x = 8000 – 16000
-400x = -8000
x = \(\frac{8000}{400}\) = 20
x = 20
x = 20 is subsituting in y = 32 – x
y = 32 – 20
y = 12
∴ Number of ₹ 100 notes = 20
Number of ₹ 500 notes = 12

Question 23.
If A = {x: x is a factor of 6}, B = {x: x is a positive even number less than 10}, then find
(i) A∪B,
(ii) A∩B,
(iii) A – B by Venn diagram.
Solution:
A = {x : x is a factor of 6} = {1, 2, 3, 6}
B = {x : x is a positive even number less than 10}
= {2, 4, 6, 8}

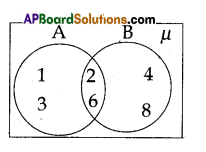
i) A∪B
A ∪ B = {1, 2, 3, 6} ∪ {2, 4, 6, 8}
A ∪ B = {1, 2, 3, 4, 6, 8}

ii) A ∩ B
A ∩ B = {1, 2, 3, 6} ∩ {2, 4, 6, 8}
= {2, 6}

iii) A – B
A – B = {1, 2, 3, 6} – {2, 4, 6, 8}
= {1, 3}

Question 24.
If the Geometric Progressions 162, 54, 18, ……. and \(\frac{2}{81}\), \(\frac{2}{27}\), \(\frac{2}{9}\),…….. have their n^th terms equal, then find the value of ‘n’.
Solution:
Given geometric progression = 162, 54, 18…

Given n^th term of these geometric progressions are equal.

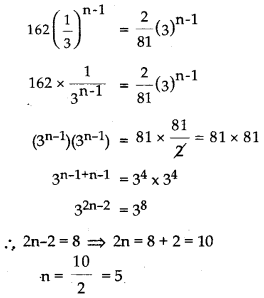
Question 25.
Find the area of shaded D region in figure, if AB CD is a square of side 10.5 cm and APD, BPC are semicircles

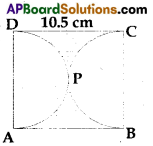
(Use π = \(\frac{22}{7}\)).
Solution:
Side of a square = 10.5 cm
Area of a square
= 10.5 × 10.5
= 110.25 cm²

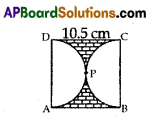
Radius of each semi circle = \(\frac{10.5}{2}\)
= 5.25 cm

Similarly area of semicircle BPC = 43.3125 cm²
∴ Sum of areas of two semicircles = 2 × 43.3125
= 86.625 cm²
∴ Area of shaded region
= Area of square ABCD – sum of areas of two semicircles
= 110.25 – 86.625
= 23.625 cm²

Question 26.
Express the following in terms of trigonometric ratios of angles between 0° and 45°.
i) sin 81° + tan 75°
ii) cos 65° + cot 75°
Solution:
i) sin 81° + tan 75°
= sin(90 – 9)° + tan(90 – 15)°
= cos 9° + cot 15°
[∵ sin(90 – θ) = cosθ
tan(90 – θ) = cotθ]

ii) cos 65° + cot 75°
= cos(90-25)° + cot(90-15)°
= sin 25° + tan 15°
[∵ cos(90 – θ) = sin θ
cot (90 – θ) = tan θ]

Question 27.
When a die is thrown once, find the probability of getting on its face :
i) 8
ii) a number less than 6
iii) a prime number
iv) a composite number
Solution:
When a die is thrown once then possible outcomes = {1, 2, 3, 4, 5, 6}
Total possible outcomes = 6.

i) 8
Let ‘E’ be the event of getting on its face is 8
No. of favourable outcomes = 0.
Probability of an event P (E)
\(=\frac{\text { No.of favourable outcomes }}{\text { Total possible outcomes }}\) = \(\frac{0}{6}\) = 0

ii) A number less than 6.
Let ‘F’ be the event of getting on its face is number less than 6.
No. of favourable outcomes = 5
Probability of an event = P(F) = \(\frac{5}{6}\)

iii) A prime number
Let ‘G’ be the event of getting on its face is prime number.
No. of favourable outcomes = 3 i.e {2, 3, 5}
Probability of an event P(G) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

iv) a composite number
Let ‘H’ be the event of getting on its face is a composite number.
No. of favourable outcomes 2
Probability of an event = P(H) = \(\frac{2}{6}\) = \(\frac{1}{3}\)

Question 28.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point ‘O’.
Show that \(\frac{\mathrm{AO}}{\mathrm{BO}}\) = \(\frac{\mathrm{CO}}{\mathrm{DO}}\).
Solution:
Given : ABCD is trapezium in which AB || DC.
Its diagonals intersect each other at the point ‘O’
To Prove: \(\frac{\mathrm{AO}}{\mathrm{BO}}\) = \(\frac{\mathrm{CO}}{\mathrm{DO}}\)

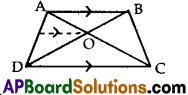
Construction: Draw a line OE parallel to AB or CD through ‘O’ and intersecting AD at E
Proof: In ∆ABD we have OE || AB
∴ By Basic proportionality theorem,
\(\frac{\mathrm{AE}}{\mathrm{ED}}\) = \(\frac{\mathrm{BO}}{\mathrm{OD}}\) ……. (1)
In ∆ADC, we have EO || DC
⇒ \(\frac{\mathrm{AE}}{\mathrm{ED}}\) = \(\frac{\mathrm{AO}}{\mathrm{OC}}\) ……. (2)
From (1) and (2) we have
\(\frac{B O}{O D}\) = \(\frac{A O}{O C}\) ⇒ \(\frac{A O}{B O}\) = \(\frac{C O}{D O}\)
Hence proved.

Section – IV
(5 × 8 = 40 M)

Note:

1. Answer all the questions.
2. Each question carries 8 marks.
3. Each question has internal choice.

Question 29.
a) Prove that \(\sqrt{2}\) + \(\sqrt{5}\) is an irrational.
OR
b) Check whether – 150 a term of the AP : 11, 8, 5, 2, ……
Solution:
a) Let us assume that \(\sqrt{2}\) + \(\sqrt{5}\) is a rational.
\(\sqrt{2}\) + \(\sqrt{5}\) = \(\frac{a}{b}\) [where a, b are integers and b ≠ 0]
squaring on both sides

∴ Since a, b are integers \(\frac{a^2+3 b^2}{2 a b}\) is rational
So \(\sqrt{5}\) is rational.
This contradicts the fact \(\sqrt{5}\) is irrational.
∴ Hence \(\sqrt{2}\) + \(\sqrt{5}\) is irrational.

OR

b) We have,
a₂ – a₁ = 8 – 11 = -3;
a₃ – a₂ = 5 – 8 = -3;
a₄ – a₃ = 2 – 5 = -3;
a_k+1 – a_k is same for k = 1, 2, 3, … . the given list of numbers is an AP.
For this AP; a = 11; d = -3
We choose to begin with the assumption that -150 is a term. Say the n^th term of this AP. We will see if an ‘n’ exists for which
a_n = -150
a + (n – 1)d = -150
11 + (n – 1)(-3) = -150
11 – 3n + 3 = -150
14 – 3n = -150
-3n = -150 – 14
-3n = 164
n = \(\frac{-164}{-3}\) = \(\frac{164}{3}\)
But n should be a positive integer.
So, -150 is not a term in the given AP.

Question 30.
a) Find the roots of the quadratic equation x² + 3x -18 = 0 by the method of completing the square.
OR
b) Two cubes each of volume 64 cm³ are joined end to end together. Find the lateral surface area and total surface area of resulting cuboid.
Solution:
a) x² + 3x – 18 = 0
x² + 3x = 18
x² + \(\frac{2}{2}\) × 3 × x = 18
x² + 2 × x × \(\frac{3}{2}\) = 18
Adding \(\left(\frac{3}{2}\right)^2\) on both sidés

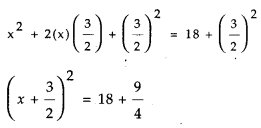
OR

b) Volume of cube (v) = 64 cm³

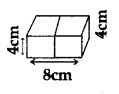
s³ = 64 cm³ = (4 cm)³
⇒ s = 4 cm
Length of the cuboid = 4 cm + 4cm = 8 cm
Surface area of the cuboid
= 2(lb + lh + bh)
= 2[8 × 4 + 8 × 4 + 4 × 4] cm²
= 2[32 + 32 + 16] cm² = 160 cm²
Lateral surface area of cuboid = 2h[l + b]
= 2 × 4[8 + 4]
= 8 × 12
= 96 cm²

Question 31.
a) Find the area of the quadrilateral whose vertices taken in order are A(1, 1), B(7, -3), C(12, 2), D(7, 21).
OR
b) If the median of 60 observations given below is 28.5, then find the values of x and y.

Class interval	0-10	10-20	20-30	30-40	40-50	50-60
Frequency	5	X	20	15.	y	5

Solution:
a) A(1, 1), B(7, -3), C(12, 2) and D(7, 21) are the vertices of quadrilateral ABCD.
Join BD, ∆ABD and ∆BCD are formed.

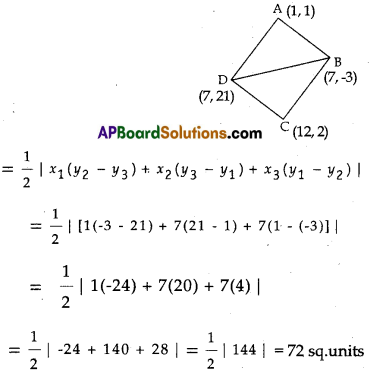
Area of ∆BCD
= \(\frac{1}{2}\) |7[(2 – 21) + 12(21 – (-3) + 7(-3 – 2)] |
= \(\frac{1}{2}\) |7(-19) + 12(24) + 7(-5)|
= \(\frac{1}{2}\) |-133 + 288 – 35| = \(\frac{1}{2}\)|-120| = 60 sq.units
∴ Area of quadrilateral ABCD
= Area of ∆ABD + Area of ∆BCD
= 72 + 60
= 132 sq.units.

OR

b) Given median value 28.5 is in the class 20-30.
So, 20-30 is the median class.

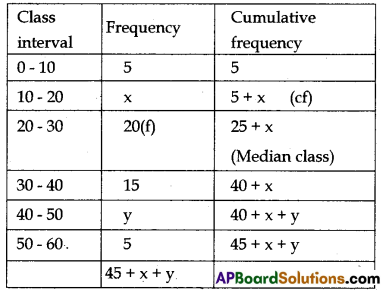
Given, total number of observations,
n = 45 + x + y = 60
⇒ x + y = 15 → 1
Also, \(\frac{\mathrm{n}}{2}\) = 30, l = 20, f = 20, cf = 5 + x, h = 10

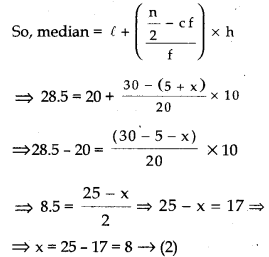
Substitute x value in eq.(1)
8 + y = -15; y = 15 – 8 = 7
So, required values; x = 8, y = 7

Question 32.
a) A straight highway leads to the foot of a tower. Ramaiah standing at the top of the tower observes a car at an angle of depression 30°. The car is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
OR
b) One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting :
i) A queen of black colour
ii) a face card
iii) a jack of diamond
iv) a club card
Solution:
a) Let the distance travelled by the car in 6 seconds = AB = x meters
Height of the tower CD = h meters
The remaining distance to be travelled by the car BC = d meters
and AC = AB + BC = (x + d) meters
∠PDA = ∠DAC = 30°
(Alternate interior angles)
∠PDB = ∠DB×C = 60°
(Alternate interior angles)

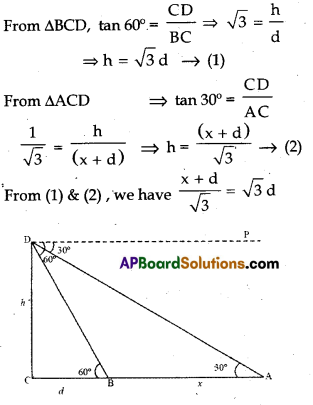
x + d = 3d; x = 2d ; d = \(\frac{x}{2}\)
Time taken to travel ‘x’ meters = 6 seconds.
Time taken to travel the distance of d meters, i.e., \(\frac{x}{2}\) meters = 3 seconds.

b) Total number of cards in a deck = 52
Total possible outcomes = 52

i) A queen of black colour
Let ‘E’ be the event of getting a queen of black colour.
No. of favourable outcomes = 2
Probability of an event E is
P(E) \(=\frac{\text { No. favourable outcomes }}{\text { Total possible outcomes }}\) = \(\frac{2}{52}\)
= \(\frac{1}{26}\)

ii) A face card
Let ‘F’ be the event of getting a face card.
favourable outcomes = 12
Probability of an event F is P(F) = \(\frac{12}{52}\)
= \(\frac{3}{13}\)

iii) A jack of diamond
Let ‘G’ be the event of getting a jack of diamond
Favourable outcomes = 1
probability of an event = P(G) = \(\frac{1}{52}\)

iv) A club card
Let ‘H’ be the event of getting a club card.
Favourable outcomes = 13
Probability of an event = P(H) = \(\frac{13}{52}\) = \(\frac{1}{4}\)

Question 33.
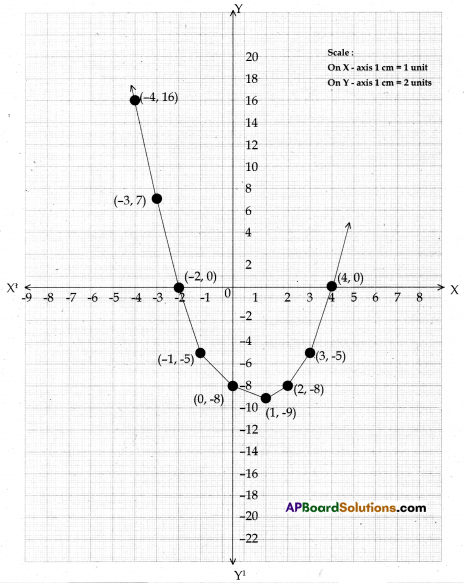
a) Draw the graph of the polynomial p(x) = x² – 2x – 8 and find its zeroes.
OR
b) Construct an isosceles triangle whose base is 6 cm and altitude is 3 cm. Then draw another triangle whose sides are 1\(\frac{1}{3}\) times the corresponding sides of the isosceles triangle.
Solution:
a) p(x) = x² – 2x – 8
Let y = x² – 2x – 8

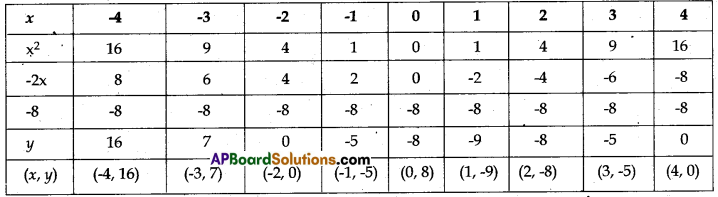
Result:

1. p(x) = x² – 2x – 8 is a quadratic equation that forms parabola.
2. p (x) = x² – 2x – 8 intersects X-axis at (-2, 0) and (4, 0)
3. Hence zeroes of p(x) are -2 and 4.

Verification:

⇒ x² – 2x -8 = 0
⇒ x² + 2x – 4x – 8 = 0
⇒ x(x + 2) – 4(x – 4) = 0
(x + 2) (x – 4) = 0
x + 2 = 0 and x – 4 = 0
x = -2 and x = 4

b)

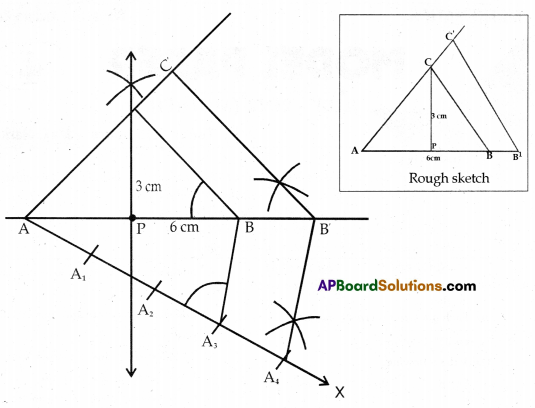
Steps of Construction:

1. Construct an isosceles triangle ABC with given measurements
2. Draw a line segment AB 6 cm and draw a perpendicular bisector of AB intersects it at ‘P.
3. Draw an arc with measure of 3 cm at the point P, it intersects perpendicular bisector at ‘C’. Join AC and BC.
4. Draw a ray AX, making an acute angle with AB on the side opposite to vertex ‘C’.
5. Locate 4 points A₁, A₂, A₃, A₄ on AX so that AA₁ = AA₂ = A₂A₃ = A₃A₄.
6. Join A₃B and draw a line through A₄ parallel to A₃B intersecting AB at B’.