AP 10th Class Maths Model Paper Set 6 with Solutions

Regularly solving AP 10th Class Maths Model Papers Set 6 contributes to the development of problem-solving skills.

AP SSC Maths Model Paper Set 6 with Solutions

Instructions :

1. In the duration of 3 hours 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the answer booklet only.
3. Question paper consists of 4 Sections and 33 questions.
4. Internal choice is available in section – IV only.
5. Answers shall be written neatly and legibly.

Section – I
(12 × 1 = 12M)

Question 1.
Which of the following point lies in Q3?
A) (3, -2)
B) (3, 2)
C) (-3, -2)
D) (- 3,2)
Solution:
C) (-3, -2)

Question 2.
Draw the graph of ax² + bx + c = 0 when b² – 4ac < 0.
Solution:

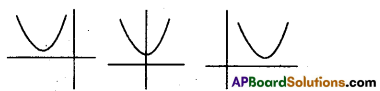
Question 3.
\(\frac{7}{5}\) is the zero of 7x – 5. Is it True/False ?
Solution:
False
p(x) = 7x – 5
p(\(\frac{7}{5}\)) = 7(\(\frac{7}{5}\)) – 5 = \(\frac{49}{5}\) – 5 = \(\frac{49-25}{5}\) = \(\frac{24}{5}\)
p(\(\frac{7}{5}\)) ≠ 0. So, \(\frac{7}{5}\) is not a zero of p(x).

Question 4.
From the figure, find ∠PAQ.

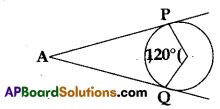
Solution:
∠PAQ = 180° – 120° = 60°

Question 5.
In 2, 4, 6, 8, 10 …….. of A.P. , common difference is ……
Solution:
2

Explanation:
2, 4, 6, 8, 10 …….. is an A.P
Common difference = d = a₂ – a₁ = 4 – 2 = 2

Question 6.
Choose the correct answer.

Statement p : Sin 45° = \(\frac{1}{\sqrt{2}}\)
Statement q : Tan 30° = \(\frac{1}{\sqrt{3}}\)
A) p true, q false
B) p false, q true
C) both p, q are true
D) both p, q are false
Solution:
C) both p, q are true

Question 7.
If the ratio of areas of two similar triangles is 2 : 1 then the ratio of their perimeters is ……..
Solution:
\(\sqrt{2}\) : 1

Question 8.
Choose the correct matching:

a) x + 2y = 4, 3x + 6y = 7, ( ) i) unique solution
b) x + 2y = 4, 3x + 6y = 12 ( ) ii) no solution
c) x + 2y = 4, 3x – y = 2 ( ) iii) infinite solutions

A) a – i, b – ii, c – iii
B) a – iii, b – ii, c – i
C) a – ii, b – iii, c – i
D) a – ii, b – i, c – iii
Solution:
C) a – ii, b – iii, c – i

Question 9.
Choose the correct matching:

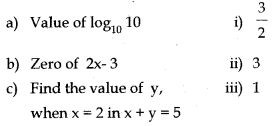
A) a – (i), b -(ii), c – (iii)
B) a – (i), b – (iii), c – (ii)
C) a – (iii), b – (i), c – (ii)
D) a – (ii), b – (iii), c – (i)
Solution:
C) a – (iii), b – (i), c – (ii)

Question 10.
If A = {1, 2} and B = {3, 4} then A∪B
Solution:
A ∪ B = {1, 2} ∪ {3, 4} = {1, 2, 3, 4}

Question 11.
If a dice is thrown, what is the probability of getting an odd number less than 3?
Solution:
\(\frac{1}{6}\)

Question 12.
In Mode = l + \(\left[\frac{f_1-f_0}{2 f_1-f_0-f_2}\right]\) × h, ‘l’ represents ….
A) lower limit
B) upper limit
C) lower boundary
D) upper boundary
Solution:
C) lower boundary

Section – II
(8 × 2 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 2 marks.

Question 13.
What value(s) of x will make DE || AB, in the given figure AD = 8 x + 9, CD = x + 3, BE = 3x + 4, CE = x.
Solution:
In ∆ABC, DE || AB
∴ By Thale’s theorem,

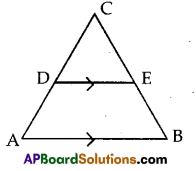
\(\frac{C D}{A D}\) = \(\frac{C E}{C B}\)
⇒ (x + 3) (3x + 4) = x (8x + 9)
⇒ 3x² + 4x + 9x + 12 = 8x² + 9x
⇒ 8x² + 9x – 3x² – 4x – 9x – 12 = 0
⇒ 5x² – 4x – 12 = 0
⇒ 5x² – 10x + 6x – 12 = 0
⇒ 5x(x – 2) + 6(x – 2) = 0
⇒ (x – 2) (5x + 6) = 0
⇒ x = 2 or x = \(\frac{-6}{5}\)

Question 14.
Is 2t – 1 = 2t + 5 a linear equation in one variable?
Solution:
2t – 1 = 2t + 5
2t – 2t = 5 + 1
0 = 6
There is no variable in it. So it is not a linear equation in one variable.

Question 15.
Determine the value of \(2^{2+\log _2^3}\)
Solution:
\(2^{2+\log _2 3}\) = 2² × \(2^{\log _2 3}\)
= 4 × \(\log _2 3\)
= 4 × 3
= 12
We know that
(i) a^{m + n} = a^m × aⁿ
(ii) \(a^{\log _a N}\) = N

Question 16.
2, 3, 5, 7, 8, 10, 15 …… is an arithmetic progression? Why ?
Solution:
Given that 2, 3, 5, 7, 8, 10, 15…………
a₂ – a₁ = 3 – 2 = 1
a₃ – a₂ = 5 – 3 = 2
a₄ – a₃ = 7 – 5 = 2
a₅ – a₄ = 8 – 7 = 1
∴ a₂ – a₁ ≠ a₃ – a₂ = a₄ – a₃ ≠ a₅ – a₄
So it is not an arithmetic progression.

Question 17.
What is the probability for drawing out a ’Red king’ from a deck of cards?
Solution:
Total deck of cards = 52
Total possible outcomes = 52
No. of favourable outcomes to drawing out a red king = 2
∴ Probability P (E)
No. of favourable out comes
\(=\frac{\text { No. of favourable out comes }}{\text { Total possible out comes }}\)
= \(\frac{2}{52}\) = \(\frac{1}{26}\)

Question 18.
Write the formula to find median of a grouped data?
Solution:
Median = l + \(\frac{\frac{n}{2}-c f}{f}\) × h
Where l = lower limit of the median class.
h = length of the median class.
f = frequency of the median class,
cf = cumulative frequency of the class preceeding the median class.

Question 19.
A cylinder and cone have bases of equal radii and are of equal heights. Show that their volumes are
in the ratio of 3 : 1.
Solution:
It is given that the bases have equal radii and are of equal heights.
∴ Ratio of the volumes of the cylinder and the cone = πr²h : \(\frac{1}{3}\)πr²h
= 1 : \(\frac{1}{3}\) = 3 : 1

Question 20.
Rinki observed a ball on the ground from the balcony of the first floor of a building at an angle of depression θ. If the height of the first floor of the building is ‘x’ meters. Draw the diagram for this data
Solution:

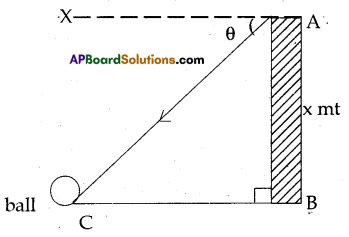
AB = height of the building = x mt
∠XAC = Angle of depression = θ

Section – III
(8 × 4 = 32 M)

Note:

1. Answer all the questions.
2. Each question carries 4 marks.

Question 21.
How many multiples of 4 lie between 10 and 250?
Solution:
The list of multiples of 4 lie between 10 and 250 is,
12, 16, 20, 24, ……., 248
Here, a = 12 ; d = 4 ; a_n = 248
a_n = a + (n – 1)d
248 = 12 + (n – 1)4
248 – 12 = (n – 1)4
(n – 1)4 = 236
n – 1 = \(\frac{236}{4}\) = 59
n = 59 + 1 = 60
∴ There are 60, multiples of 4 lie between 10 and 250.

Question 22.
Solve the following pair of equations:
\(\frac{2}{x}\) + \(\frac{3}{y}\) = 13 ; \(\frac{5}{x}\) – \(\frac{4}{y}\) = -2
Solution:
Observe the given pair of equations. They are not linear equations.
We have 2(\(\frac{1}{x}\)) + 3(\(\frac{1}{y}\)) = 13 …….. (1)
5(\(\frac{1}{x}\)) – 4(\(\frac{1}{y}\)) = -2 …….. (2)
If we substitute \(\frac{1}{x}\) = p and \(\frac{1}{y}\) = q, we get a pair of linear equations:
2p + 3q = 13 ………… (3)
5p – 4q = -2 ………. (4)
[Coefficients of q are 3 and 4 and their L.C.M. is 12. Using the elimination method:]

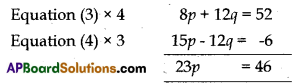
[‘q’ has opposite sign, so we add the two equations.]
p = \(\frac{46}{23}\) = 2
Substitute the value of p in equation (3)
2(2) + 3q = 13 ; 3q = 13 – 4 = 9
q = \(\frac{46}{23}\)
But, \(\frac{1}{x}\) = p = 2 ⇒ x = \(\frac{1}{2}\)
\(\frac{1}{y}\) = q = 3 ⇒ y = \(\frac{1}{3}\)

Question 23.
Find two consecutive positive integers, sum of whose squares is 613.
Solution:
Let the first positive integer be x
Then the consecutive positive integer is x + 1
Sum of the squares = x² + (x + 1)²
= x² + x² + 2x + 1
= 2x² + 2x + 1
Given sum of the squares = 613
∴ 2x² + 2x + 1 = 613
2x² + 2x + 1 – 613 = 0
2x² + 2x – 612 = 0
x² + x – 306 = 0
x² + 18x – 17x – 306 = 0
x(x + 18) – 17 (x + 18) = 0
(x + 18)(x – 17)
x + 18 = 0 or x – 17 = 0
x + 18 = 0 gives x = -18
x – 17 = 0 gives x = 17
For x = 17 its consecutive positive integer is x + 1 = 17 + 1 = 18.
Two consecutive positive integers are 17, 18.

Question 24.
Find all the zeroes of 2x⁴ – 3x³ – 3x² + 6x – 2, if you know that two of its zeroes are \(\sqrt{2}\) and –\(\sqrt{2}\).
Solution:
Since two of the zeroes are \(\sqrt{2}\) and –\(\sqrt{2}\), therefore we can divide by

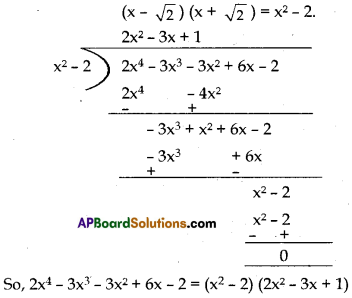
Now, by splitting -3x, we factorize 2x² – 3x + 1 as (2x – 1) (x – 1). So, its zeroes are given by x = \(\frac{1}{2}\) and x = 1. Therefore, the zeroes of the given polynomial are \(\sqrt{2}\), –\(\sqrt{2}\) and 1 and \(\frac{1}{2}\).

Question 25.
Prove that the points A (-7, -3), B (5, 10), C (15, 8) and D (3, – 5) taken in order are the vertices of a
parallelogram.
Solution:
Let A(-7, -3), B(5, 10), C(15, 8) and D(3, -5) be the given points.


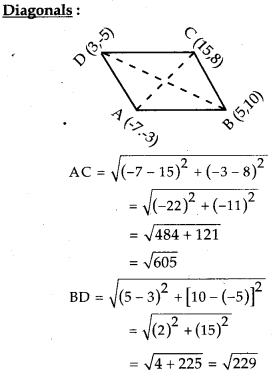
Opposite sides AB = CD, BC = DA
Diagonals AC ≠ BD
Therefore ABCD is a parallelogram.
The given points taken in order form a parallelogram.

Question 26.
A heap of rice is in the form of a cone of diameter 12 m. and height 8 m. Find its volume? How much canvas cloth is required to cover the heap?
(Use π = 3.14)
Solution:
Diameter of the conic heap of rice = 12 m
∴ Its radius(r) = –\(\frac{12}{2}\)m = 6 m
height (h) = 8 m
Its volume (v) = \(\frac{1}{3}\)πr²h

Required canvas cloth to cover the heap
= Curved surface area of heap
= πrl = 3.14 × 6 × 10 m²
= 188.4 m²

Question 27.
Show that

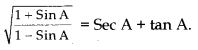
Solution:

Question 28.
A die is thrown once. Find the probability of getting
i) a prime Number
ii) a number lying between 2 and 6
iii) an odd number
iv) multiple of 3.
Solution:
When a die is thrown, sample space S = {1, 2, 3, 4, 5, 6}
i) Let A denotes the event of getting a prime number. Then A = {2, 3, 5}
So, required probability = P(A)
= \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

ii) Let B denote the event of getting a number between 2 and 6.
Then, B = {3, 4, 5}
∴ Required probability = P(B) = \(\frac{n(B)}{n(S)}\)
\(\frac{3}{6}\) = \(\frac{1}{2}\)

iii) Let C denotes the event of getting an odd number. Then C = {1, 3, 5}
So, required probability, P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}\)
\(\frac{3}{6}\) = \(\frac{1}{2}\)

iv) Let D denotes the event of getting multiple of 3. Then D = {3, 6}
No. of favorable outcomes = 2
So, required probability,
p(D) = \(\frac{\mathrm{n}(\mathrm{D})}{\mathrm{n}(\mathrm{S})}\)
Probability = P (D) = \(\frac{2}{6}\) = \(\frac{1}{3}\)

Section-IV
(5 × 8 = 40 M)

Note:

1. Answer all the questions.
2. Each question carries 8 marks.
3. There is an internal choice for each question.

Question 29.
A = {x : x set of even prime}
B = {x : x is a natural number < 12}
C = {x : x is a multiple of 4 less than or equal to 12}
D = {x : x is a factors of 12}
Find
(i) A ∪ B
(ii) B ∩ C
(iii) C – D
(iv) A – D

(OR)

If log \(\left(\frac{x+y}{3}\right)\) = \(\frac{1}{2}\)(log x + log y), then find the value of \(\frac{x}{y}\).
Solution:
A = {x : x is set of even prime} = {2}
B = {x : x is a natural number < 12}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
C = {x : x is a multiple of 4 less than or equal to 12}
= {4, 8, 12}
D = {x : x is a factor of 12} = {1, 2, 3, 4, 6, 12}

(i) A∪B
A∪B= {2} ∪ {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}

(ii) B ∩ C
B ∩ C = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} ∩ {4, 8, 12} = {4, 8}

(iii) C – D
C – D = {4, 8, 12} – {1, 2, 3, 4, 6, 12} = {8}

(iv) A – D = {2} – {1, 2, 3, 4, 6, 12} = { } = φ

(OR)

Question 30.
For which acute angle ‘θ’

(OR)

A motor boat whose speed is 18 km/h in still water. It takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solution:

(OR)

Let the speed of the stream be x km/h
Therefore, the speed of the boat upstream = (18 – x) km/h and the speed of the boat downstream = (18 + x) km/h.
The time taken to go upstream distance 24
\(\frac{\text { distance }}{\text { speed }}\) = \(\frac{24}{18-x}\) hours.
Similarly, the time taken to go down-stream
= \(\frac{24}{18+x}\) hours
According to the question,
= \(\frac{24}{18-x}\) – \(\frac{24}{18+x}\) = 1
i.e., 24(18 + x) – 24(18 – x)
= (18 – x)(18 + x)
i.e., x² + 48x – 324 = 0
Using the quadratic formula, we get
x = \(\frac{-48 \pm \sqrt{48^2+1296}}{2}\) = \(\frac{-48 \pm \sqrt{3600}}{2}\)
= \(\frac{-48 \pm 60}{2}\) = 6 (or) -54
Since x is the speed of the stream, it cannot be negative. So, we ignore the root x = – 54. Therefore, x = 6 gives the speed of the stream as 6 km/hr.

Question 31.
The mean pocket allowance is 18/-. Find the missing frequencies.

Daily pocket allowance	11-13	13-15	15-17	17-19	19-21	21-23	23-25
Number of Children	7	6	9	13	f	5	4

(OR)

Find the co-ordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Solution:
Given that, mean pocket allowance is ₹ 18.
We will find the mean of the given data and equalize it with 18 to find the value of ‘f’.

(OR)

Let P and Q be the points of trisection of AB is AP = PQ = QB.
Therefore P divides AB internally in the ratio 1 : 2

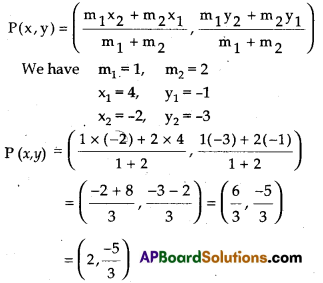
Now, Q also divides AB internally in the ratio 2 : 1
We have x₁ = 4, y₁ = -1, x₂ = -2, y₂ = -3.
m₁ = 2; m₂ = 1

Therefore the coordinates of the point of trisection of the line joining are p(2, \(\frac{-5}{3}\)) and Q(0, \(\frac{-7}{3}\))

Question 32.
State and prove Pythagoras Theorem.

(OR)

The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 15 seconds,
the angle of elevation changes to 30°. If the jet plane is flying at a constant height of 100\(\sqrt{3}\) meter, find the speed of the jet plane. (\(\sqrt{3}\) = 1.732)
Solution:
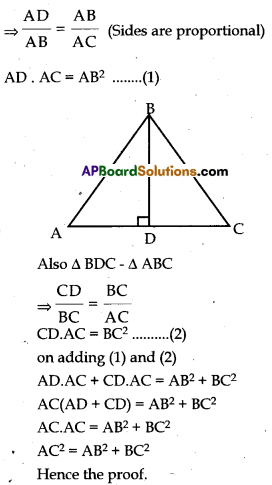
Statement: In a right triangle, the square of hypotenuse is equal to the sum of the squares of the other two sides.
Given : ∆ABC is the right triangle right angled at B.
RTP: AC² = AB² + BC²
Construction: Draw BD ⊥ AC
Proof: ∆ADB ~ ∆ABC

(OR)

Let D is the initial position of the jet plane which moves to C in 15 seconds.
A is the point on the ground from where we are observing. Then


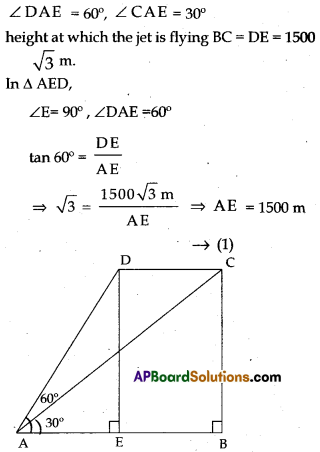
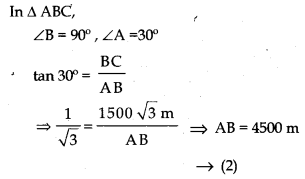
From (1) & (2)
Distance that jet flied
= CD = BE = AB – AE
= 4500 m – 1500 m = 3000 m
So, speed of the flight
= \(\frac{3000 \mathrm{~m}}{15 \text { seconds }}\) = 200 m/s

Question 33.
Draw the graph of p(x) = x² – x – 12 and find its zeroes. Justify your answer.
(OR)
Draw a circle of radius 6 cm. From a point 10 cm away from its centre construct the pair of tangents to the circle and measure their lengths. Verify by using Pythogaras theorem.
Solution:
p(x) = x² – x – 12
y = x² – x – 12


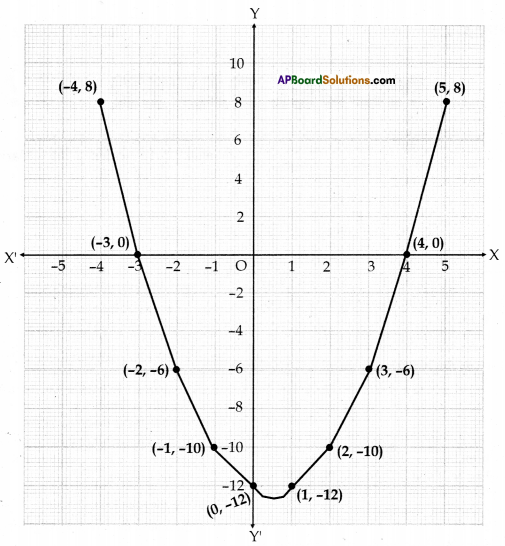
-3 and 4 are zeroes of the quadratic polynomial because (-3, 0) and (4, 0) are intersection points of X axis.
Justification: x² – x – 12 = 0 ⇒ x² – 4x + 3x – 12 ⇒ (x – 4) (x + 3) = 0
x – 4 = 0 and x + 3 = 0 x = 4, x = -3 zeroes of p(x) = -3, 4.

(OR)

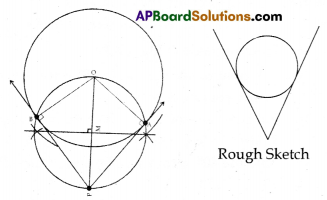
Construction:

1. Draw a circle of radius 6 cm. Let its centre be ‘O’
2. Let a point P is at a distance of 10 cm from the centre ‘O’
3. Draw the perpendicular bisector of PO which cuts it at the mid point M.
4. Taking M as centre with radius PM or MO, we draw a circle that intersects the given circle at two points A and B.
5. Join PA and PB. These are the required tangents of the circle.

Proof:
From the figure, PO = 10 cm, OA = 6 cm
Also ∆POA is a right angled triangle.
By Pythagoras theorem,
PO² = PA² + OA² ⇒ PA² = PO² – OA² = 10² – 6² = 100 – 36 = 64
∴ PA = \(\sqrt{64}\) = 8 cm
In OPB, ∠OBP = 90°. OB = 6 cm, OP = 10 cm.
By Pythagoras theorem OP² = OB² + BP²
⇒ BP² = OP² – OB² ⇒ = 10² – 6²
= 100 – 36 = 64 ⇒ BP = \(\sqrt{64}\)
= 8 cm