AP 10th Class Maths Model Paper Set 1 with Solutions

Regularly solving AP 10th Class Maths Model Papers Set 1 contributes to the development of problem-solving skills.

AP SSC Maths Model Paper Set 1 with Solutions

Instructions :

1. In the duration of 3 hours 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the answer booklet only.
3. Question paper consists of 4 Sections and 33 questions.
4. Internal choice is available in section – IV only.
5. Answers shall be written neatly and legibly.

Section – I
(12 × 1 = 12M)

Note:

1. Answer all the questions in one word or phrase.
2. Each question carries 1 mark.

Question 1.
“Every set is a subset of itself”. This statement belongs to which property?
Solution:
Reflexive property

Question 2.
In the A.P. -3, –\(\frac{1}{2}\), 2, ……. a₁₁
A) 11
B) 22
C) -22
D) -11
Answer:
B) 22

Question 3.
If x = 2 is a solution of the equation
2x² – kx + 5 = 0 then find the value of k.
Solution:
\(\frac{13}{2}\)

Question 4.
Statement (A): If log 625 = k. log 5 then the value of k = 5′
Statement (B): log₉ Sin 90° = 1
A) Both A and B are true
B) A is true, B is false
C) A is false, B is true
D) Both A and B are false
Solution:
D) Both A and B are false

Question 5.
Read the following data and answer the question

5 pencils and 7 pens together cost Rs 50, where as 7 pencils and 5 pens together cost Rs 46. Write a pair of linear equations from the data with variables x and y.
Solution:
5x + 7y = 50 [Let pencils be x, pens be y]
7x + 5y = 46

Question 6.
Write the zeros of the polynomial (shown in the graph).

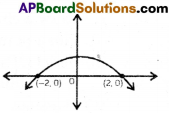
Solution:
-2, 2

Question 7.
If 4cos²θ = 3 then find sinθ.
Solution:
4cos²θ = 3
cos²θ = \(\frac{3}{4}\)
sin²θ = 1 – cos²θ
sin²θ = 1 – \(\frac{3}{4}\) = \(\frac{1}{4}\)
sinθ = \(\sqrt{\frac{1}{4}}\) = \(\frac{1}{2}\)
sinθ = \(\frac{1}{2}\)

Question 8.
“A person is flying a kite at an angle of elevation α and the length of thread from his hand to kite is ‘l’. Draw diagram for the situation.
Solution:

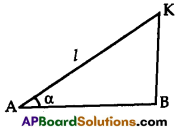
Question 9.
Read the following and answer question
If a line is passing through (2, 3) and (2, -3) then
1. the line is parallel to X – axis
2. the line is parallel to Y – axis
3. the slope of the line is not defined
4. the slope of the line is zero Which of the above are correct ?
Solution:
2 and 3

Question 10.
If P(E) = 0.09 then find P(not E) in percentage.
Solution:
P(E) = 0.09
P(E) + P\((\overline{\mathrm{E}})\) = 1
P\((\overline{\mathrm{E}})\) = 1 – P(E) = 1 – 0.09
P\((\overline{\mathrm{E}})\) = 0.91
P\((\overline{\mathrm{E}})\) in percentage = \(\frac{91}{100}\) × 100 = 91%

Question 11.
Match the following.

Choose the correct answer
A) a – iii, b – i, c – ii
B) a – ii, b – iii, c – i
C) a – ii, b – i, c – iii
D) a – i, b – iii, c – ii
Solution:
B) a-ii, b-iii, c-i

Question 12.
How many number of parallel tangents are drawn to a circle with a given tangent?
Solution:
one.

Section – II
(8 × 2 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 2 marks.

Question 13.
An empty set is a finite set. Is this statement true or false? Why?
Solution:
“An empty set is a finite set”. It is True.
Because number of elements in a null set is 0.
n(φ) = 0
It is possible to count the number of elements in the empty set.

Question 14.
A cylinder and cone have bases of equal radii and are of equal heights. Show that their volumes are in the ratio of 3 : 1.
Solution:
It is given that the bases have equal radii are of equal heights.
∴ Ratio of the volumes of the cylinder and the cone = πr²h : \(\frac{1}{3}\)πr²h
= 1 : \(\frac{1}{3}\) = 3 : 1

Question 15.
Solve 3x + 2y = 11; 2x + 3y = 4 using elimination method.
Solution:
3x + 2y = 11 …….. (1)
2x + 3y = 4 ………. (2) (Step 1)
Let us eliminate ‘y’ from the equations. The coefficients of ‘y’ in the given equations are 2 and 3. L.C.M. of 2 and 3 is 6.
So, multiply equation (1) by 3 and equation (2) by 2.

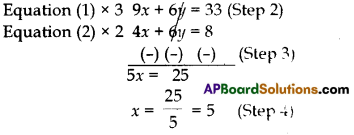
Substitute x = 5, in equation (1)
3(5) + 2y = 11
2y = 11 – 15 = – 4 ⇒ y = \(\frac{-4}{2}\) = -2
(Step 5)
Therefore, the required solution is x = 5, y = – 2.

Question 16.
Why are \(\frac{1}{4}\) and -1 zeroes of the polynomial p(x) = 4x² + 3x – 1?
Solution:
p(x) = 4x² + 3x – 1

Question 17.
Find the co-ordinates of the point, which divides the line segment joining (2, 0) and (0, 2) in the ratio 1 : 1.
Solution:
The point dividing the line segment joining (2, 0) and (0, 2) in the ratio 1: 1 is nothing but the mid point.
Coordinates of the required point
= \(\left(\frac{\mathrm{x}_1+\mathrm{x}_2}{2}, \frac{\mathrm{y}_1+\mathrm{y}_2}{2}\right)\)
= \(\left(\frac{2+0}{2}, \frac{0+2}{2}\right)\)
= \(\left(\frac{2}{2}, \frac{2}{2}\right)\) = (1, 1)

Question 18.
Find the roots of x – \(\frac{1}{x}\) = 3, x ≠ 0.
Solution:

Question 19.
PA is a tangent of length 8 cm to a circle whose radius OA = 6 cm. Then find PO.
Solution:

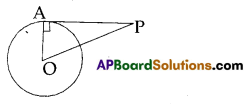
Tangent of a circle is perpendicular to its radius at the point of contact.
∠OAP = 90°
Using Pythagoras theorem,
OP² = OA² + PA²
= 6² + 8² = 36 + 64 = 100
∴ OP = \(\sqrt{100}\) = 10 cm

Question 20.
A boy observed the top of an electric pole at an angle of elevation of 60° when the observation point is 8 meters away from the foot of the pole.

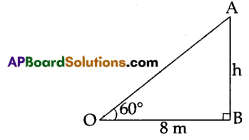
Solution:
From the figure, in triangle OAB

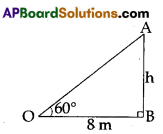
Let height of the pole = AB = h meters distance between observation point and foot of the pole OB = 8 meters, ∠AOB = 60°,
tan 60° = \(\frac{A B}{O B}\) ⇒ \(\sqrt{3}\) = \(\frac{h}{8}\)
⇒ h = 8\(\sqrt{3}\) m

Section – III
(8 × 4 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 4 marks.

Question 21.
A die is thrown once. Find the probability of getting
i) a prime number;
ii) a number lying between 2 and 6;
Solution:
When a die is thrown, sample space
S = {1, 2, 3, 4, 5, 6}

i) Let A denotes the event of getting a prime number. Then A = {2, 3, 5}
So, required probability = P(A)
= \(\frac{n(A)}{n(S)}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

ii) Let B denote the event of getting a number between 2 and 6.
Then, B = {3, 4, 5}
∴ Required probability = P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}\)
= \(\frac{3}{6}\) = \(\frac{1}{2}\)

Question 22.
“The area of a rectangular plot is 528m². The length of the plot (in meters) is one more than twice its breadth.” Represent the above situation in the form of quadratic equation.
Solution:
Let the breadth be x mts.
Length of the plot is one more than twice its breadth.
∴ Length = (2x + 1)mts
Area of the plot = Length × Breadth.
= (2x + 1) x = (2x² + x) square mts.
Given area of the plot = 528 sq. mts.
Therefore, 2x² + x = 528
2x² + x – 528 = 0
The required quadratic equation is 2x² + x – 528 = 0 (x = breadth)

Question 23.
Prove that \(\sqrt{2}\) + \(\sqrt{3}\) is irrational.
Solution:
Let us suppose that \(\sqrt{2}\) + \(\sqrt{3}\) is rational.
Let \(\sqrt{2}\) + \(\sqrt{3}\) = \(\frac{a}{b}\), where a, b are integers and b ≠ 0
Therefore,
Squaring on both sides, we get

Since a, b aré integers, \(\frac{a^2+b^2}{2 a b}\) is rational, and so, \(\sqrt{3}\) is rational.
This contradicts the fact that \(\sqrt{3}\) is irrational.
Hence, \(\sqrt{2}\) + \(\sqrt{3}\) is irrational.

Question 24.
In a retail market, fruit vendors were selling oranges kept in packing baskets. These baskets contained varying number of oranges. The following was the distribution of oranges.

Number of oranges	10-14	15-19	20-24	25-29	30-34
Number of baskets	15	110	135	115	25

Find the mean number of oranges kept in each basket. Which method of finding the mean did you choose ?
Solution:

By using the assumed mean method, 22 oranges are kept on average in a box.

Question 25.
Find the 31^st term of an AP whose 11^th term is 38 and 16th term is 73.
Solution:
We have,
a₁₁ = a + (11 – 1)d = a + 10d = 38 → (1)
a₁₆ = a + (16 – 1)d = a + 15d = 73 → (2)
Solving the equations (1) and (2) by using elimination method

Substitute
d = 7 in (1)
a + 10(7) = 38
a + 70 = 38 ⇒ a = 38 – 70 = -32
31^st term = a₃₁ = a + (31 – 1)d
= a + 30d
= -32 + 30(7)
= -32 + 210
= 178
The 31st term of the AP is 178.

Question 26.
In ∆ACB, ∠C = 90° and CD ⊥ AB. Prove that \(\frac{B C^2}{A C^2}\) = \(\frac{B D}{A D}\)

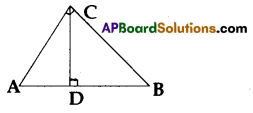
Solution:
In ∆ACD and ∆ABC we have ∠A = ∠A
(∴ Common angle)
∠ADC = ∠ACB = 90° [given]
∴ ∆ACD ~ ∆ABC ……….. (1)
Similarly ∆BCD ~ ∆ABC ……. (2)
From (1) and (2), we get
∆ACD ~ ∆BCD
⇒ \(\frac{\mathrm{AC}}{\mathrm{BC}}\) = \(\frac{\mathrm{AD}}{\mathrm{BD}}\)
[∴ ratios of corresponding sides]
⇒ \(\frac{B C^2}{A C^2}\) = \(\frac{B C^2}{A C^2}\)

Question 27.
A chord in a circle of radius 6 cm is making an angle 60° at the centre. Find the length of the chord.
Solution:
Given the radius of the circle
OA = OB = 6 cm
∠AOB = 60°
Draw OC ⊥ AB
Clearly OC is an angular bisector.
∴ ∠COB = 30°

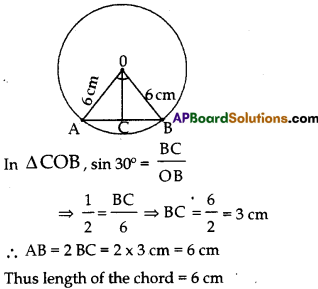
Question 28.
Verify that 1, -1 and -3 are the zeroes of the cubic polynomial x³ + 3x² – x – 3 and check the relationship between zeroes and the coefficients.
Solution:
Comparing the given polynomial with ax³ + bx² + cx + d
We get a = 1; b = 3; c = -1; d = -3
Further p(x) = x³ + 3x² – x – 3
p(1) = (1)³ + 3(1)² – 1 – 3
= 1 + 3 – 1 – 3 = 4 – 4 = 0
p(-1) = (-1)³ + 3(-1)² – (-1) – 3
= -1 + 3 + 1 – 3 = 4 – 4 = 0
p(-3) = (-3)³ + 3(-3)² – (-3) – 3
= -27 + 27 + 3 – 3
= 30 – 30 = 0
Therefore 1, -1 and -3 are zeroes of x³ + 3x² – x – 3
So, we take α = 1; β = -1 and γ = -3 Now,
α + β + γ = 1 + (-1) + (-3) = 1 – 4 = -3 = \(\frac{-3}{1}\)
= \(\frac{-b}{a}\)
αβ + βγ + γα = (1)(-1) + (-1)(-3) + (-3)(1)
= -1 + 3 – 3 = -1 = \(\frac{-1}{1}\) = \(\frac{\mathrm{c}}{\mathrm{a}}\)
αβγ = 1 × (-1) × (-3) = 3 = \(\frac{-(-3)}{1}\) = \(\frac{-\mathrm{d}}{\mathrm{a}}\)
From the above, the coefficients and the zeroes of the polynomial are equal.

Section – IV
(5 × 8 = 40 M)

Note:

1. Answer all the questions.
2. Each question carries 8 marks.
3. Each question has internal choice.

Question 29.
The median of the following data is 525. Find the values of x and y, if the total frequency is 100. Here, CI stands for class interval and Fr for frequency.

CI	0-100	100-200	200-300	300-400	400-500	500-600	600-700	700-800	800-900	900-1000
Fr	2	5	X	12	17	20	y	9	7	4

(OR)
Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).
Solution:

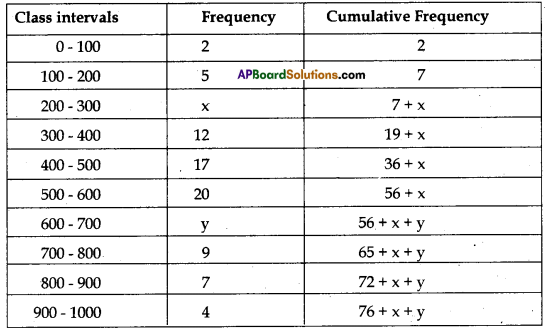
Given that, the total frequency, n = 100
U.C. ⇒ 2 + 5 + x + 12 + 17 + 20 + y + 9 + 7 + 4 = 100
⇒ x + y = 100 – 76 = 24 → (1)
\(\frac{n}{2}\) = 50
Median = 525 which is in the class 500 – 600.
So, l = 500, f = 20, cf = 2 + 5 + x + 12 + 17 = x + 36,
h = 100
So, 525 = l + \(\frac{\left(\frac{n}{2}-c f\right)}{f}\) × h ⇒ 525 = 500 + \(\left[\frac{50-(x+36)}{20}\right]\) × 100
⇒ 525 = 500 + 5 (-x + 14)
⇒ 5(-x + 14) = 25 ⇒ -x + 14 = 5
⇒ x = 9 → (2)
Put (2) in (1), 9 + y = 24 ⇒ y = 15
So, required values are x = 9 and y = 15

(Or)

Vertices of quadrilateral = A (-4, -2), B (-3, -5), C (3, -2), D (2, 3).
Here x₁ = -4, y₁ = -2, x₂ = -3, y₂ = -5, x₃ = 5, y₃ = -2, x₄ = 2, y₄ = 3
Area of quadrilateral ABCD

Question 30.
If log \(\left(\frac{x+y}{3}\right)\) = \(\frac{1}{2}\)(log x + log y) then find the value of \(\frac{x}{y}\) + \(\frac{y}{x}\)
(OR)
A cylindrical container is filled with ice-cream whose diameter is 12 cm. and height is 15 cm. The whole ice-cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is twice the diameter of its base, find the diameter of the ice-cream cone.
Solution:

(Or)

Let the radius of the base of conical ice cream be x cm.
∴ The height of the conical ice-cream
= 2(diameter) = 2(2x) = 4x cm.
Volume of ice-cream cone.
= Vol. of conical portion + Vol. of hemispherical portion

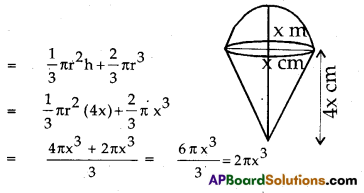
Diameter of cylindrical container = 12 cm
Its height = 15cm
Its volume = πr²h
= π(6)²15 = 54oπ
Number of children = 10
⇒ \(\frac{\text { Vol.of cylindrical container }}{\text { Vol of each ice-cream cone }}\) = 10
⇒ \(\frac{540 \pi}{2 \pi x^3}\) ⇒ x³ = \(\frac{540 \pi}{2 \times 10}\) = 27
⇒ x = \(\sqrt[3]{27}\) = 3
∴ Diameter of ice-cream cone = 2x = 2(3)
= 6 cm.

Question 31.
“A boat goes 30 km upstream and 44 km downstream in 10 hours. In 13 hours it can go 40 km upstream and 55 kin downstream. Determine the speed of the stream and that of the boat in still water.”

(OR)

From a deck of 52 playing cards, King, Ace and 10 of Clubs were removed and remaining cards were well shuffled. If a card is drawn at random from the remaining, find the probability of getting a card of i) Club
ii) Ace
iii) Diamond king
iv) Club 5.
Solution:
Let the speed of the boat be x km /hr.
The speed of the stream be y km / hr.
Relative speed upstream = (x – y) km /hr
Relative speed down the stream = (x + y) km / hr
Distance travelled to up stream = 30 km.
Time taken to up = \(\frac{30}{x-y}\) hrs.
Distance travelled to down stream 44 km.
Time taken = \(\frac{44}{x+y}\) hrs
Total time taken = \(\frac{30}{x-y}\) + \(\frac{44}{x+y}\)
Given total time taken = 10 hrs;
\(\frac{30}{x-y}\) + \(\frac{44}{x+y}\) = 10 ……….. (1)
Distance travelled to up stream = 40 km.
Time taken to up = \(\frac{40}{x-y}\) hrs
Distance travelled to down stream = 55 km.
Time taken = \(\frac{55}{x+y}\) hrs
Given total time taken = 13 hrs ;
\(\frac{40}{x-y}\) + \(\frac{55}{x+y}\) = 13 ……… (2)
44\(\left(\frac{1}{x+y}\right)\) + 30\(\left(\frac{1}{x-y}\right)\) = 10 ;
55\(\left(\frac{1}{x+y}\right)\) + 40\(\left(\frac{1}{x-y}\right)\) = 13
If we substitute \(\frac{1}{x+y}\) = p and \(\frac{1}{x-y}\) = q
we get a pair of linear equations
44p + 30q = 10 …….. (3)
55p + 40q = 13 …… (4)
Elimination Method:


Substitute the value of x in (5)
8 + y = 11 ; y = 11 – 8 = 3
Speed of the boat = 8 km / hr
Speed of the stream = 3 km / hr

(Or)

Total number of playing cards =52
Number of cards removed 3
Number of remaining cards = 52 – 3 = 49

i) Let E be the event of getting a card of club.
n(E) = 10.
P(E) = \(\frac{n(E)}{n(S)}\) = \(\frac{10}{49}\)

ii) Let F be the event or getting a card of Ace.
n(F) = 3
P(F) = \(\frac{\mathrm{n}(\mathrm{F})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{49}\)

iii) Let K be the event of getting a card of Diamond King.
n(K) = 1
P(K) = \(\frac{\mathrm{n}(\mathrm{K})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{1}{49}\)

iv) Let G be the event of getting a card of club 5
n(G) = 1
P(G) = \(\frac{\mathrm{n}(\mathrm{G})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{1}{49}\)

Question 32.
ABD is a triangle right angled at A and AC ⊥ BD Show that
(i) AB² = BC.BD
(ii) AC² = BC.DC

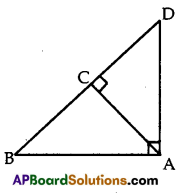
(OR)
i) Show that sec²θ + cosec²θ = sec²θ. cosec²θ.
ii) Prove that \(\sqrt{\frac{1+\cos \theta}{1-\cos \theta}}\) = cosec θ + cot θ.
Solution:
Given: In figure, ABD is a triangle right angled at A and AC ⊥ BD

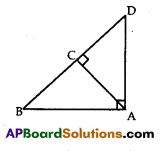
To prove:
(i) AB² = BC.BD
(ii) AC²
= BC.DC
(iii) AD² = BD.CD.
Proof:
i) In ∆BAC and ∆BDA we have
∠BCA = ∠BAD = 90° [given]
∠ABC = ∠ABD [common angle]
∴ By AA similarity criterion,
∆BAC ~ ∆BDA
Corresponding sides of two similar triangles are in same ratio.
⇒ \(\frac{\mathrm{BA}}{\mathrm{BD}}\) = \(\frac{\mathrm{BC}}{\mathrm{BA}}\) ⇒ AB² = BC.BD.

ii) In ∆ACB and ∆DCA we have
∠ACB = ∠DCA = 90° [given]
∠BAC = ∠ADC [proved in (i)]
∴ By AA similarity criterion,
AC BC
∆ACB ~ ∆DCA ⇒ \(\frac{A C}{D C}\) = \(\frac{B C}{A C}\)
[ratios of corresponding sides]
⇒ AC² = BC.DC.

(Or)

i) sec² θ + cosec² θ = sec²θ.cosec²θ.

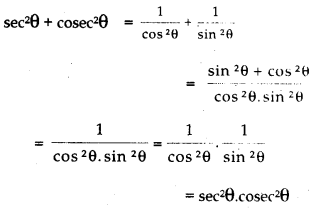
ii)

Question 33.
Solve the quadratic polynomial x² – 3x – 4 by graphical method.
(OR)
Draw two tangents to a circle of radius 2.5 cm, from a point ‘P’ at a distance of 7 cm from its centre.
Solution:
Let p(x) = y = x² – 3x -4 be the given quadratic polynomial.

Table of coordinates:

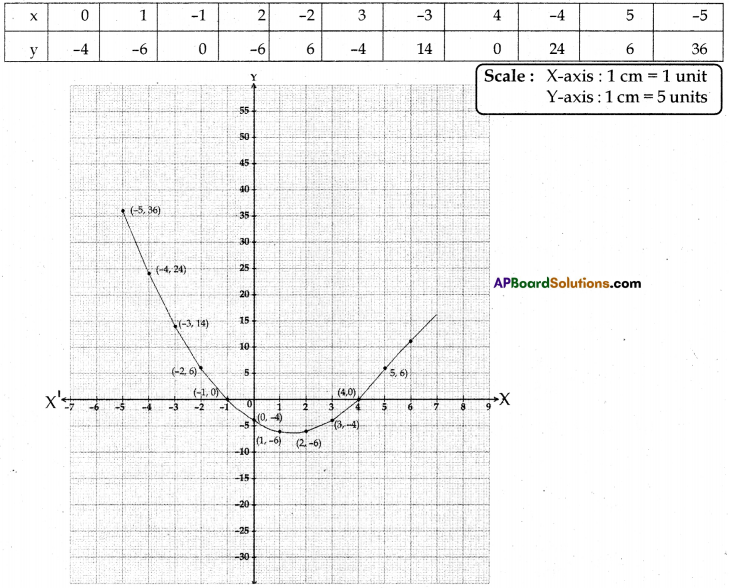
From the graph, we can observe that the curve intersects the X-axis at (-1, 0) and (4, 0).
∴ The zeroes of the given polynomial are -1 and 4.

(OR)

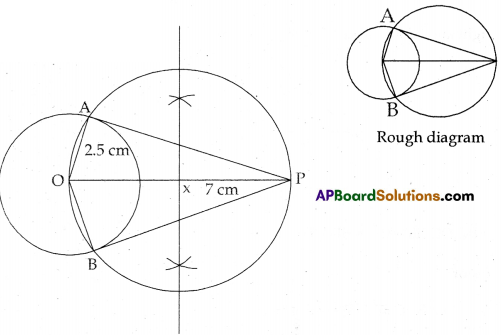
Steps of construction:

1. Draw a circle with radius 2.5 cm with centre O
2. Plot a point P such that OP = 7 cm
3. Draw perpendicular of OP and draw a circle with radius XP = XO from X
4. Join the two tangents PA and PB