AP 10th Class Maths Question Paper June 2023 with Solutions

Regularly solving AP 10th Class Maths Model Papers and AP 10th Class Maths Question Paper June 2023 contributes to the development of problem-solving skills.

AP SSC Maths Question Paper June 2023 with Solutions

Time : 3.15 hours
Max. Marks : 100

Instructions:

1. In the duration of 3 hours 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the answer booklet only.
3. Question paper consists of 4 Sections and 33 questions.
4. Internal choice is available in section – IV only.
5. Answers shall be written neatly and legibly.

Section – I
(12 × 1 = 12 M)

Note:

1. Answer all the questions in one word or phrase.
2. Each question carries 1 mark.

Question 1.
Express 2^x = y in logarithmic form.
Solution:
log₂y = x

Question 2.
If p(t) = t² – 1, then p(-1) = …….
Solution:
0

Question 3.
Write a linear equation in two variables for the following situation.
“The cost of 5 pens and 3 pencils is ₹54”.
Solution:
5x + 3y = 54

Question 4.
Nature of the roots of the quadratic equation 2x² – 6x + 3 = 0 is
A) Real
B) Equal
C) Distinct
D) Real and distinct
Solution:
D) Real and distinct

Question 5.
If 18, a, b, -3 are in A.P., then a + b = …….
A) 19
B) 7
C) 11
D) 15
Solution:
D) 15

Question 6.
Find the centroid of the triangle whose vertices are (-3, -5), (-2, 4) and (8, -2).
Solution:
(1, -1)

Question 7.
The length of the tangent to a circle of radius 7cm which is drawn from an external point at a
distance of 25 cm away from its centre is
A) 12 cm
B) 24 cm
C) 26 cm
D) 13 cm
Solution:
B) 24 cm

Question 8.
Statement I : Volume of a hemisphere of radius ‘r’ is \(\frac{4}{3}\) π r².
Statement II : Surface area of a sphere of radius ‘r’ is 4 π r²
Now, choose the correct answer:
A) Both Statements are true
B) Both Statements are false
C) Statement I is true, Statement II is false
D) Statement I is false, Statement II is true.
Solution:
D) Statement I is false, Statement II is true.

Question 9.
Express sec θ in terms of tan θ.
A) \(\sqrt{1-\tan ^2 \theta}\)
B) \(\sqrt{1+\tan ^2 \theta}\)
C) \(\sqrt{\tan ^2 \theta-1}\)
D) \(\frac{\sqrt{1+\tan \theta}}{\tan \theta}\)
Solution:
B) \(\sqrt{1+\tan ^2 \theta}\)

Question 10.
Draw a rough figure for the following situation. “A person is flying a kite at an angle of elevation ‘α’ and the length of thread from his hand to kite is ‘l’.”
Solution:

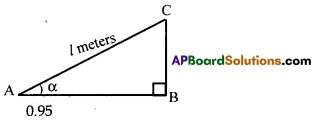
Question 11.
If P(E) = 0.05, then P(\(\overline{\mathrm{E}}\)) = ……..
Solution:
0.95

Question 12.
Assertion (A): If the mode of the data 5, 5, 5, 6, 6, 6, 2, 2, 2, 3, 3, 3, x is 6, then the value of x = 6.
Reason (R) : Mode is always at the centre of the data.
Now, choose the correct answer:
A) Both Assertion and Reason are true and Reason is supporting Assertion
B) Both Assertion and Reason are true, but Reason is not supporting Assertion
C) Assertion is true, but Reason is false
D) Assertion is false, but Reason is true.
Solution:
C) Assertion is true, but Reason is false

Section – II
(8 × 2 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 2 marks.

Question 13.
How will you show that (17 × 11 × 2) + (17 × 11 × 5) is a composite number ?
Solution:
(17 × 11 × 2) + (17 × 11 × 5)
= 17 × 11 × (2 + 5)
= 17 × 11 × 7
Since it has more than two factors it is a composite number.
By the fundamental theorem of arithmetic every composite number can be expressed as a product of primes.

Question 14.
Check whether the following equations are consistent or inconsistent. 2x – 3y = 8, 4x – 6y = 9
Solution:
2x – 3y – 8 = 0
4x – 6y – 9 = 0
img 23
Since \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{b_1}{b_2}\) ≠ \(\frac{c_1}{c_2}\), the given equations are inconsistent.

Question 15.
Find the 6^th term of the Geometric Progression whose a₁ = -12 and r = \(\frac{1}{3}\).
Solution:

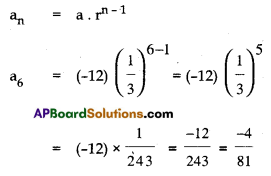
Question 16.
Find the slope of the line joining the two points A(3, -2) and B(-6, 5).
Solution:
Slope (m) = \(\frac{y_2-y_1}{x_2-x_1}\) = \(\frac{5-(-2)}{-6-3}\)
= \(\frac{5+2}{-9}\) = \(-\frac{7}{9}\)

Question 17.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:

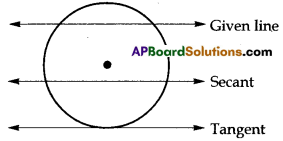
Question 18.
Find the volume of a cone whose height is 10 cm and the radius of the base is 3.5 cm.
Solution:
Radius of cone (r) = 3.5 cm = \(\frac{7}{2}\) cm
Its height (h) = 10 cm
Volume of a cone (V) = \(\frac{1}{3} \pi r^2 h\)
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 10
= \(\frac{770}{6}\) = 128.33 cm³

Question 19.
Express sin 81° + tan 81° in terms of trigonometric ratios of angles between 0° and 45°.
Solution:
sin 81° + tan 81° = sin (90° – 9°) + tan (90° – 9°)
= cos 9° + cot 9°
[∵ sin (90° – A) = cos A
tan (90° – A) = cot A]

Question 20.
A die is thrown once. Find the probability of getting
(i) a prime number,
(ii) an odd number.
Solution:
i) Let ‘E₁‘ be an event of getting a prime number,
E₁ = {2, 3, 5}
S = {1, 2, 3, 4, 5, 6}
∴ P(E₁) = \(\frac{\mathrm{n}\left(\mathrm{E}_1\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

ii) Let ‘E₂‘ be an event of getting an odd number,
E₂ = {1, 3, 5}
∴ P(E₂) = \(\frac{\mathrm{n}\left(\mathrm{E}_2\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

Section – III
(8 × 4 = 32 M)

Note:

1. Answer all the questions.
2. Each question carries 4 marks.

Question 21.
If A and B are two non-empty sets, then draw the venn diagrams of A∪B, A∩B, A – B and B – A.
Solution:

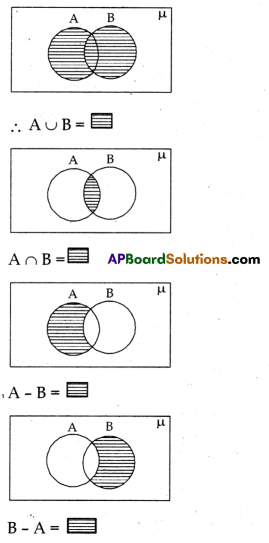
Question 22.
Find a quadratic polynomial with zeroes -2 and \(\frac{1}{3}\).
Solution:
Given: The zero’s of quadratic polynomial are -2 and \(\frac{1}{3}\)
Quadratic polynomial with zeros α, β is

Question 23.
Solve the following pair of linear equations.
3x – 5y = -1,
x – y = -1.
Solution:
Given : 3x – 5y = -1 → (1)
x – y = -1 → (2)

Substituting y = -1 in (1)
3x – 5(-1) = -1
⇒ 3x = -6
⇒ x = \(\frac{-6}{3}\) = -2
∴ x = -2, y = -1
Alternate Method :
Given : 3x – 5y = -1 → (1)
x – y = -1 → (2)
From (2), y = x + 1 → (3)
Substituting y = x + 1 in equation (1)
3x – 5(x + 1) = -1
-2x = -1 + 5
x = \(\frac{4}{-2}\) = -2
Substituting x = -2 in equation (3)
y = x + 1
y = -2 + 1 = -1
∴ x = -2, y = -1

Question 24.
A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades. (Use π = \(\frac{22}{7}\))
Solution:
Given : length of each blade, r = 25 cm
Angle of sweeping x° = 115°
Area swept by two wipers = 2 × Area swept by each blade
= 2 × \(\frac{x^{\circ}}{360^{\circ}}\)πr²
= 2 × \(\frac{115^{\circ}}{360^{\circ}}\) × \(\frac{22}{7}\) × (25)²
= 1254.96 sq. units.

Question 25.
Two cubes each of volume 64 cm³ are joined end to end together. Find the total surface area of the resulting cuboid.
Solution:
Let ‘a’ be an edge of a cube
Given : volume of the cube = 64 cm³
∴ a³ = 64 = 4³

The dimensions of resulting cuboid are
length l = 8 cm
breadth b = 4 cm
height h = 4 cm
Total surface area of the cuboid = 2(lb + bh + lh)
= 2[8 × 4 + 4 × 4 + 8 × 4]
= 2[32 + 16 + 32]
= 2[80] = 160 cm²

Question 26.
A tower stands vertically on the ground. From a point which is 15 metres away from the foot of the tower, the angle of elevation of the top of the tower is 45°. What is the height of the tower ?
Solution:

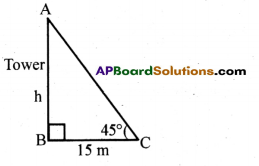
From the figure., in triangle ABC
Given, BC = Distance from the tower = 15 m,
Angle of elevation = ∠C = 45°
Let, height of the tower AB = h meters
tan 45° = \(\frac{\mathrm{h}}{15}\) ⇒ 1 = \(\frac{\mathrm{h}}{15}\) ⇒ h = 15m

Question 27.
Write the formula to find the median of a grouped data and explain the terms in it.
Solution:
Median, M = l + \(\left(\frac{\frac{\mathrm{n}}{2}-\mathrm{cf}}{\mathrm{f}}\right)_h\)
l = lower boundary of the median class,
h = size of the median class (class size)
n = number of observations
cf = cumulative frequency of class preceding the median class
f = frequency of median class

Question 28.
ABC is a right triangle right angled at C. Let BC = a, CA = b, AB = c and let ‘p’ be the length of perpendicular from C on AB, prove that pc = ab.
Solution:
Given, ABC is a right triangle right angled at C

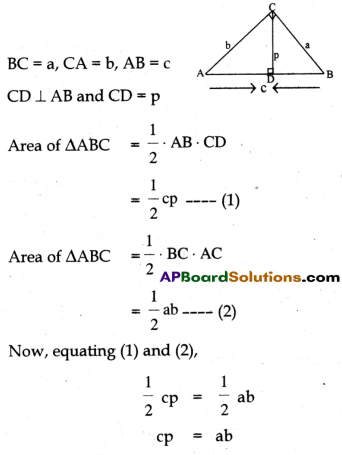
Section – IV
(5 × 8 = 40 M)

Note:

1. Answer all the questions.
2. Each question carries 8 marks.
3. Each question has internal choice.

Question 29.
a) Prove that \(\sqrt{3}\) is irrational.
OR
b) Prove that \(\sqrt{\frac{1+\cos \theta}{1-\cos \theta}}\) = cosecθ + cotθ.
Solution:
a) Let us assume \(\sqrt{3}\) is rational.
If it is rational, then there must exist two integers ‘r’ and ‘s'(s ≠ 0) such that \(\sqrt{3}\) = \(\frac{\mathrm{r}}{\mathrm{s}}\).
If ‘r’ and ‘s’ have a common factor other than 1, then we divide by the common factor to get \(\sqrt{3}\) = \(\frac{a}{b}\), where ‘a’ and ‘b’ are co-primes. So b\(\sqrt{3}\) = a
On squaring both sides and rearranging, we get
3b² = a²
∴ 3 divides a²
⇒ 3 divides a
So, we can write a = 3c, for some integer ‘c’
Substituting for a, we get 3b² = (3c)²
⇒ 3b² = 9c²
⇒ b² = 3c²
This means 3 divides b² ⇒ 3 divides b
∴ Both ‘a’ and ‘b’ have 3 as a common factor. But this contradicts the fact that ‘a’ and ’b’ are co-primes.
This contradiction has arisen because of our assumption that \(\sqrt{3}\) is rational.
Thus our assumption is false.
\(\sqrt{3}\) is irrational.

b)

Question 30.
a) If A = {2, 3, 5, 7}, B = {2, 4, 6, 8}, C = {2, 5, 8, 11}, D = {3, 5, 7, 9} then find
i) A∪B
ii) A – B
iii) A∩B
iv) B – A
v) C – D
vi) B – C
vii) B∩D
viii) C∪D

OR

b) Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Solution:
a) A = {2, 3, 5, 7}
B = {2, 4, 6, 8}
C = {2, 5, 8, 11}
D = {3, 5, 7, 9}
(i) A ∪ B = {2, 3, 5, 7} ∪ {2, 4, 6, 8}
= {2, 3, 4, 5, 6, 7, 8}
(ii) A – B = {2, 3, 5, 7} – {2, 4, 6, 8} = {3, 5, 7}
(iii) A ∩ B = {2, 3, 5, 7} ∩ {2, 4, 6, 8} = {2}
(iv) B – A = {2, 4, 6, 8} – {2, 3, 5, 7} = {4, 6, 8}
(v) C – D = {2, 5, 8, 11} – {3, 5, 7, 9}
= {2, 8, 11}
(vi) B – C = {2, 4, 6, 8} – {2, 5, 8, 11} = {4, 6}
(vii) B ∩ D = {2, 4, 6, 8} ∩ {3, 5, 7, 9}
= { } = φ
(viii) C ∪ D = {2, 5, 8, 11} ∪ {3, 5, 7, 9}
= {2, 3, 5, 7, 8, 9, 11}

b) Let A (4, -1) and B(-2, -3)
Let P and Q are the points of trisection of AB i.e. AP = PQ = QB
∴ P divides AB internally in the ratio 1 : 2

Now, Q also divides AB internally in the ratio 2: 1
So the coordinates of Q are
Q(x, y) = \(\left(\frac{2(-2)+1(4)}{2+1}, \frac{2(-3)+1(-1)}{2+1}\right)\)
= \(\left(\frac{-4+4}{3}, \frac{-6-1}{3}\right)\)
Q(x, y) = \(\left(0, \frac{-7}{3}\right)\)
Therefore, the coordinate of the points of trisection of the line segment are
P(2, \(\frac{-5}{3}\) and Q(0, \(\frac{-7}{3}\))

Question 31.
a) In an AP, given a = 5, d = 3, a_n = 50, find ‘n’ and ‘S_n‘.
OR
b) Find the mean of the following frequency distribution.

Class Interval	10-20	20-30	30-40	40-50	50-60
Frequency	15	110	135	115	25

Solution:
a) Given, a = 5, d = 3, a<sub.n = l = 50
We know that a_n = a + (n – 1)d
∴ 50 = 5 + 3(n – 1)3
3(n – 1) = 50 – 5
3(n – 1) = 45
n – 1 = 15
∴ n = 16

To find S_n:

(OR)

S_n = \(\frac{n}{2}\)[a + l] = \(\frac{16}{2}\)[5 + 50]
= 8(55) = 440

b)

∴ Mean of the given frequency distribution is 35.625

Alternate Method:

Question 32.
a) The diagonal of a rectangular field is 60 metres more than the shorter side. If the longer side is 30 metres more than the shorter side, find the sides of the field.
OR
b) One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
i) a King of red colour,
ii) a face card
iii) a Jack of hearts,
iv) a spade.
Solution:
a) Let the shorter side of a rectangle is ‘x’m.
Given:
longer side, y = (30 + x) m
diagonal = (60 + x) m

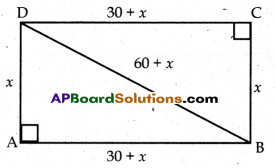
By Pythagoras theorem,
BD² = AD² + AB²
(60 + x)² = x² + (30 + x)²
3600 + 120x + x² = 900 + 60x + x² + x²
x² – 60x – 2700 = 0
x² – 90x + 30x – 2700 = 0
x(x – 90) + 30(x – 90) = 0
(x + 30) (x – 90) =0
∴ x = 90 (or) -30
x can’t be negative.
Shorter side = 90 m
Longer side = 30 + 90 = 120 m

b) Number of cards in the deck n(S) = 52
i) Number of favourable outcomes to get a king of red colour = n(E₁) = 2
Probability of getting a king of red colour
P(E₁) = \(\frac{n\left(E_1\right)}{n(S)}\) = \(\frac{2}{52}\) = \(\frac{1}{26}\)

ii) Number of favourable outcomes to get a face card = n(E₂) = 12
Probability of getting a face card
P(E₂) = \(\frac{\mathrm{n}\left(\mathrm{E}_2\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{12}{52}\) = \(\frac{3}{13}\)

iii) Number of favourable outcomes to get a jack of hearts = n(E₃) = 1
Probability of getting a jack of hearts
P(E₃ = \(\frac{\mathrm{n}\left(\mathrm{E}_3\right)}{\mathrm{n}(\mathrm{S})}\)) = \(\frac{1}{52}\)

iv) Number of favourable outcomes to get a spade = n(E₄) = 13
Probability of getting a spade
P(E₄ = \(\frac{\mathrm{n}\left(\mathrm{E}_4\right)}{\mathrm{n}(\mathrm{S})}\)) = \(\frac{13}{52}\) = \(\frac{1}{4}\)

Question 33.
a) Draw the graph of the polynomial
p(x) = x² + 3x – 4 and find its zeroes.
OR
b) Construct an isosceles triangle whose base is 5 cm and altitude is 4 cm. Then draw another triangle whose sides are 1\(\frac{1}{3}\) times the corresponding sides of the isosceles triangle.
Solution:
a)

x	-4	-3	-2	-1	0	1	2	3	4
y = x2 + 3x – 4	0	-4	-6	-6	-4	0	6	14	24
(x,y)	(-4,0)	(-3,-4)	(-2,-6)	(-1,-6)	(0,-4)	(1,0)	(2,6)	(3,14)	(4,24)

1 and -4 are zeroes of the quadratic polynomial because (1, 0) and (-4, 0) are intersection points of X – axis.

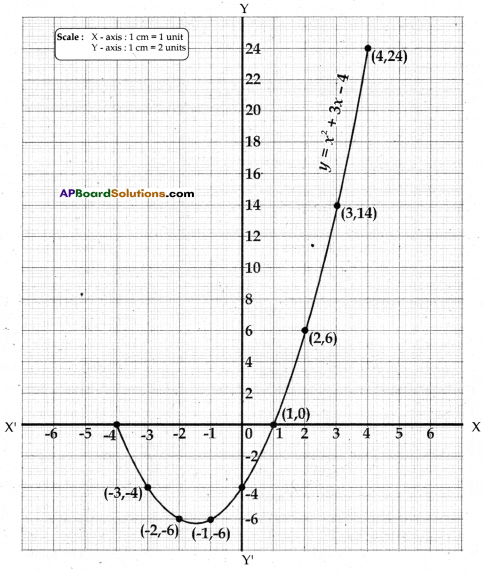
b)
Draw a line AX
Locate points A₁, A₂, A₃, A₄ such
that AA₁ = A₁A₂ = A₂A₃ = A₃A₄

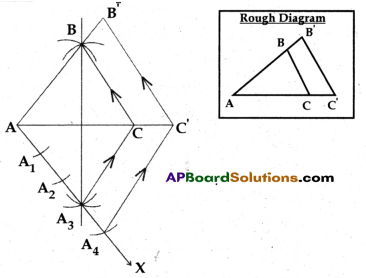
Join A₃ and C
Extend the line AC
Draw a line parallel to A₃C and let it meets the line AC at C’
Extend the line AB
Draw a line parallel to BC and let it meets the line AB at B’