AP 10th Class Maths Question Paper April 2023 with Solutions

Regularly solving AP 10th Class Maths Model Papers and AP 10th Class Maths Question Paper April 2023 contributes to the development of problem-solving skills.

AP SSC Maths Question Paper April 2023 with Solutions

Time : 3.15 hours
Max. Marks : 100

Instructions:

1. In the duration of 3 hours 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the answer booklet only.
3. Question paper consists of 4 Sections and 33 questions.
4. Internal choice is available in section – IV only.
5. Answers shall be written neatly and legibly.

Section – I
(12 × 1 = 12 M)

Note:

1. Answer all the questions in one word or a phrase.
2. Each question carries 1 mark.

Question 1.
Find the LCM of 12,15 and 21.
Solution:
420

Question 2.
Write the following set in roster form :
A = {x : x is a natural number less than 6}.
Solution:
A = {1, 2, 3, 4, 5}

Question 3.
Choose the correct answer satisfying the following statements:
Statement (P) : The degree of the quadratic polynomial is 2.
Statement (Q) : Maximum no. of zeroes of a quadratic polynomial is 2.
A) Both (P) and (Q) are true
B) (P) is true, (Q) is false
C) (P) is false, (Q) is true
D) Both (P) and (Q) are false
Solution:
A) Both (P) and (Q) are true

Question 4.
Assertion : 3x + 6y = 3900, x + 2y = 1300 represent coincident lines and have infinite number of solutions.
Reason : If a₁x + b₁y = c₁, a₂x + b₂y = c₂ and \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\) then, these lines are coincident lines.

Choose the correct answer :
A) Both Assertion and Reason are true, Reason is supporting the Assertion.
B) Both Assertion and Reason are true, but Reason is not supporting the Assertion.
C) Assertion is true but the Reason is false.
D) Assertion is false, but the Reason is true.
Solution:
A) Both Assertion and Reason are true, Reason is supporting the Assertion.

Question 5.
The number of roots of the equation 5x² – 6x – 2 = 0 is ……….
Solution:
‘2’

Question 6.
State Thales theorem.
Solution:
Thales theorem:
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then the other two sides are divided in the same ratio.

Question 7.
Find the number of tangents drawn at the end points of the diameter.
Solution:
‘2’

Question 8.
Find the volume of a cube, whose side is 4 cm.
Solution:
64 cm³

Question 9.
Match the following:

Choose the correct answer:
A) P → (i), Q → (ii), R → (iii)
B) P → (iii), Q → (i), R → (ii)
C) P → (iii), Q → (ii), R → (i)
D) P → (i), Q → (iii), R → (ii)
Solution:
B) P → (iii), Q → (i), R → (ii)

Question 10.
“You are observing top of your school building at an angle of elevation 60° from a point which is at 20 meters distance from foot of the building”. Draw a rough diagram to the above situation.
Solution:

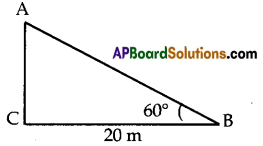
Question 11.
If P(E) = 0.05, what is the probability of not ‘E’ ?
Solution:
P(not E) = 0.95

Question 12.
Find the mean of the given data : 2,3, 7, 6, 6, 3, 8
Solution:
‘5’

Section – II
(8 × 2 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 2 marks.

Question 13.
If A = {3, 4, 5, 6), B = {5, 6, 7, 8, 9}, then illustrate A∩B in Venn diagram.
Solution:
A ∩ B = {5, 6}

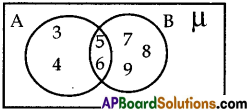
Question 14.
6 pencils and and 4 pens together cost ₹ 50 whereas 5 pencils and 6 pens together cost ₹ 46. Express the above statements in the form of linear equations.
Solution:
Let cost of each pencil ₹ x
Let cost of each pen ₹ y
∴ 6x + 4y = 50
5x + 6y = 46

Question 15.
Check whether (x – 2)² + 1 = 2x – 3 is a quadratic equation or not.
Solution:
(x – 2)² + 1 = 2x – 3
x² – 4x + 4 + 1 = 2x – 3
x² – 6x + 8 = 0 is a quadratic equation as it is in the form of ax² + bx + c = 0

Question 16.
Write the formula to find n^th term of AP and explain the terms in it.
Solution:
n^th term of Ap
a_n : a + (n – 1)d
a : first term
d : common difference

Question 17.
Find the distance between the two points (7, 8) and (-2, 3).
Solution:
A(x₁, y₁): (7, 8) B(x₂, y₂) : (-2, 3)
AB = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
AB = \(\sqrt{(-2-7)^2+(3-8)^2}\)
= \(\sqrt{(-9)^2+(-5)^2}\)
= \(\sqrt{81+25}\)
AB = \(\sqrt{106}\) units

Question 18.
From a point Q, the length of the tangent to a circle is 24 cm, and the distance of Q from the centre is 25 cm. Find the radius of the circle.
Solution:

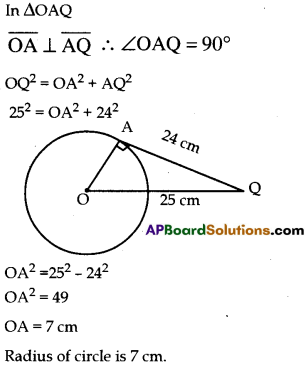
Question 19.
If cos A = \(\frac{12}{13}\), then find sin A and tan A.
Solution:

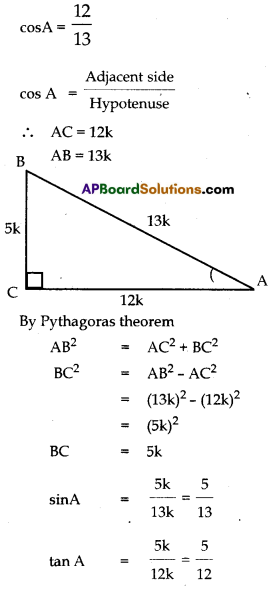
Question 20.
A die is thrown once, find the probability of getting
i) a prime number
ii) an odd number.
Solution:
Let ‘E₁‘ be an event of getting a prime number,
E₁ = {2, 3, 5}
S = {1, 2, 3, 4, 5, 6}
∴ P(E₁) = \(\frac{n\left(E_1\right)}{n(S)}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
Let ‘E₂‘ be an event of getting an odd number,
E₂ = {1, 3, 5}

Section – III
(8 × 4 = 32 M)

Note:

1. Answer all the questions.
2. Each question carries 4 marks.

Question 21.
Find ‘x’, if 2 log 5 + \(\frac{1}{2}\) log 9 – log 3 = log x.
Solution:
Given 2 log5 + \(\frac{1}{2}\) log 9 – log 3 = log x
⇒ log5² + log \(\sqrt{9}\) – log 3 = log x
⇒ log 25 + log 3 – log 3 = log x
⇒ log 25 = log x
∴ x = 25

Question 22.
Check whether -3 and 3 are the zeroes of the polynomial x⁴ – 81.
Solution:
Given polynomial
p(x) = x⁴ – 81
p(-3) = (-3)⁴ – 81
= 81 – 81 = 0
∴ -3 is zero of p(x)
p(3) = (3)⁴ – 81
= 81 – 81
= 0
∴ 3 is zero of p(x)

Question 23.
Solve the pair of linear equations using elimination method.
3x + 2y = -1 2x + 3y = -9
Solution:
Given 3x + 2y = -1 → (1)
2x + 3y = -9 → (2)

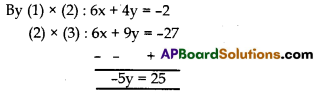
Substituting y = -5 in (1)
3x + 2(-5) = -1
3x – 10 = -1
3x = 9
x = 3

Question 24.
Rohan’s mother is 26 years older than him. The product of their ages after 3 years will be 360 years. Write the quadratic equation to find Rohari’s present age.
Solution:
Let Rohans present age = x years
Rohan’s mother’s present age = x + 26 years
After 3 years Rohan’s age = x + 3 years
After 3 years Rohan’s mother’s age = x + 29 years
By the problem:
(x + 3) (x + 29) = 360
x² – 32x + 87 = 360
x² + 32x – 273 = 0

Question 25.
Draw a tangent to a given circle with centre ‘O’ from a point ‘R’ outside the circle. How many tangents can be drawn to the circle from that point?
Solution:

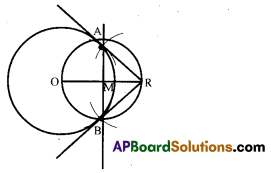
We can draw 2 tangents to the circle from R

Question 26.
An oil drum is in the shape of a cylinder having the following dimensions :
Diameter is 2 m and height is 7 meters. The painter charges ₹ 3 per m² to paint the drum. Find the total charges to be paid to the painter for 10 drums.
Solution:
Given: d = 2m
r = 1 m
h = 7m
T.S.A. of oil drum = 2πr (r + h)
= 2 × \(\frac{22}{7}\) × (1) × (8)
= 16(3.14) m² = 50.28 m²
Total charge paid for painting 10 drums
= 50.28 × 10 × 3 = ₹ 1508.40

Question 27.
Show that \(\frac{1-\tan ^2 A}{\cot ^2 A-1}\) = tan² A.
Solution:

Question 28.
A survey conducted on 20 households in a locality by a group of students resulted in the following frequency table for the number of family members in household.

Family size	1-3	3-5	5-7	7-9	9-11
No. of families	: 7	8	2	2	1

Find the mode of the data.
Solution:

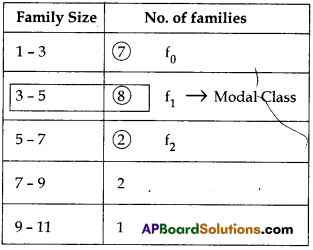
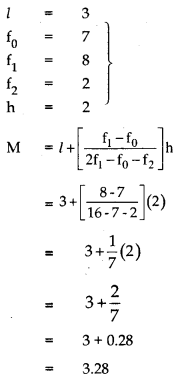
Section – IV
(5 × 8 = 40 M)

Note:

1. Answer all the questions.
2. Each question carries 8 marks.
3. Each question has internal choice.

Question 29.
a) Prove that 6 + \(\sqrt{2}\) is irrational.
(OR)
b) Show that a₁, a₂, a₃,…….. a_n form an AP where a_n is defined as below.
i) a_n = 3 + 4n
ii) a_n = 9 – 5n
Also find the sum of the first 15 terms in each case.
Solution:
a) Let us assume that 6 + \(\sqrt{2}\) is rational.
That is, we can find coprimes ‘a’ and ‘b’ (b ≠ 0)
such that 6 + \(\sqrt{2}\) = \(\frac{a}{b}\).
\(\sqrt{2}\) – \(\frac{a}{b}\) – 6 = \(\frac{a-6 b}{b}\) → (1)
Since ‘a’ and ‘b’ are integers, the RHS of equation (1)
\(\frac{a-6 b}{b}\) is rational, b
So the LHS \(\sqrt{2}\) also rational.
But this contradicts the fact that \(\sqrt{2}\) is irrational.
This contradiction has arisen because of our incorrect assumption that 6 + \(\sqrt{2}\) is rational.
So, we conclude that 6 + \(\sqrt{2}\) is irrational.

(OR)

b) Case i:
As a_n = 3 + 4n
a₁ = 3 + 4 = 7
a₂ = 3 + 4(2) = 11
a₃ = 3 + 4(3) = 15
List of numbers becomes 7, 11, 15,…….
Here, 11 – 7 = 15 – 11 = 4 and so on
So it forms on AP where a = 7, d = 4
Now S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₁₅ = \(\frac{15}{2}\)[2(7) + 14(4)]
= \(\frac{15}{2}\)(14 + 56) = 525

Case ii :
As a_n = 9 – 5n
a₁ = 9 – 5 = +4
a₂ = 9 – 5(2) = -1
a₃ = 9 – 5(3) = -6
List of numbers becomes 4, -1, -6,……….
Here -1 -4 = -6- (-1) = -5 and so on
So it forms an AP where a = 4, d = -5
Now S₁₅ = \(\frac{15}{2}\)[2(4) + 14(-5)]
= \(\frac{15}{2}\)(8 – 70)
= -465

Question 30.
a) Find the volume of the largest right circular cone that can be cutout of a cube whose edge is 7 cm.
(OR)
b) If A = {1, 2, 3, 4, 5}; B = {3, 4, 5, 6, 7}; C = {1, 3, 5, 7}; D = {2, 4, 6, 8}
Find :
i) A∪B
ii) B∪C
iii) A∪D
iv) B – D
v) A∩B
vi) B∩D
vii) C∩D
viii) A – D
Solution:
a) Edge of the cube = 7 cm
The right circular cone that can be cutout of the cube is largest if, height of the cone and diameter of the base of the cone are equal to the edge of the cube
height of the cone edge of the cube.
Height of the cone = h = 7 cm
Diameter of the base of
the cone = d = 7 cm
Base radius = r = \(\frac{7}{2}\) cm
Volume of the cone = \(\frac{1}{3}\) ∙ πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 7
= \(\frac{539}{2}\)
= 89\(\frac{5}{6}\) cm³

(OR)

b) Given A = {1, 2, 3, 4, 5), B {3, 4, 5, 6, 7}, C = {1, 3, 5, 7}, D = {2, 4, 6, 8}

(i) A∪B = {1, 2, 3, 4, 5}∪{3, 4, 5, 6, 7}
= {1, 2, 3, 4, 5, 6, 7}
(ii) B∪C = {3, 4, 5, 6, 7} ∪ {1, 3, 5, 7}
= {1, 3, 4, 5, 6, 7}
(iii) A∪D = {1, 2, 3, 4, 5} ∪ {2, 4, 6, 8}
= {1, 2, 3, 4, 5, 6, 8}
(iv) B – D = {3, 4, 5, 6, 7} – {2, 4, 6, 8}
= {3, 5, 7}
(v) A∩B = {1, 2, 3, 4, 5) ∩ {3, 4, 5, 6, 7}
= {3, 4, 5}
(vi) B∩D = {3, 4, 5, 6, 7} ∩ {2, 4, 6, 8}
= {4, 6}
(vii) C∩D = {1, 3, 5, 7} ∩ {2, 4, 6, 8} = { }
(viii) A – D = {1, 2, 3, 4, 5} – {2, 4, 6, 8} = {1, 3, 5}

Question 31.
a) The distribution below gives the weights of 30 students of class. Find the median weight of the students.

Weight (in kg)	Number of students
40-45	2
45-50	3
50-55	8
55-60	6
60-65	6
65-70	3
70 – 75	2

(OR)
b) Find the value of ’b’ for which the points A(1, 2), B(-1, b), C(-3, -4) are collinear.
Solution:
a)

(OR)

b) If A(1, 2), B(-1, b), C(-3, -4) are collinear then the area formed by

Question 32.
a) A 1.5 m tall boy is looking at the top of a temple which is 30 meter in height from a point at certain distance. The angle of elevation from his eye to the top of the crown of the temple increases from 30° to 60° as he walks towards the temple. Find the distance he walked towards the temple.
(OR)
b) One card is drawn from a well – shuffled deck of 52 cards. Find the probability of getting
i) a king of red colour
ii) a face card
iii) a jack of hearts
iv) a spade.
Solution:
a) Height of the boy AB = 1.5 m
Heigt h of the temple = CD = 30 m

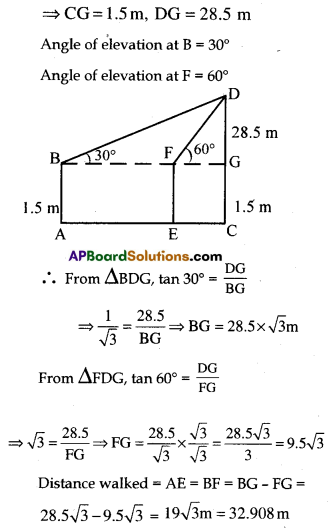
b)
Number of cards in the deck n(S) = 52
i) Number of favourable outcomes to get a king of red colour = n(E₁) = 2
Probability of getting a king of red colour P(E₁) = \(\frac{\mathrm{n}\left(\mathrm{E}_1\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{2}{52}\) = \(\frac{1}{26}\)

ii) Number of favourable outcomes to get a face card = n(E₂) = 12
Probability of getting a face card P(E₂) = \(\frac{\mathrm{n}\left(\mathrm{E}_2\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{12}{52}\) = \(\frac{3}{13}\)

iii) Number of favourable outcomes to get a jack of hearts = n(E₃) = 1
Probability of getting a jack of hearts P(E₃) = \(\frac{\mathrm{n}\left(\mathrm{E}_3\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{1}{52}\)

iv) Number of favourable outcomes to get a spade n(E₄) = 13
Probability of getting a spade P(E₄) = \(\frac{\mathrm{n}\left(\mathrm{E}_4\right)}{\mathrm{n}(\mathrm{S})}\) = \(\frac{13}{52}\) = \(\frac{1}{4}\)

Question 33.
a) Construct a triangle of sides 5 cm, 5 cm and 6 cm. Then, construct a triangle similar to it, whose sides are 2/3 of the corresponding sides of the triangle.
(OR)
b) Draw a graph of p (x) = x² – 3x – 4 and hence find the zeroes of the polynomial.
Solution:
a)
1) Construct the triangle with given measurements.
2) Draw a ray BX.

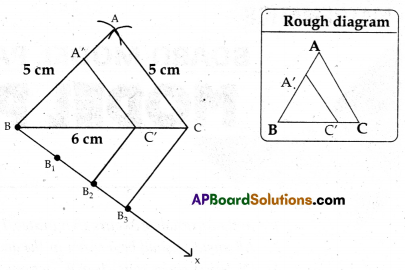
3) Locate 3 points B₁, B₂, B₃ on BX so that BB₁ = B₁B₂ = B₂B₃.
4) Join B₃ and draw a line through B₂ parallel to B₃C intersecting BC at C’.
5) Draw a line through C’ parallel to CA which intersects AB at A’.
So, ∆A’BC’ is the required triangle.

b) Let y = x² – 3x – 4

x	-2	-1	0	1	2	3	4	5
y = x2 – 3x – 4	6	0	-4	-6	-6	-4	0	6
x, y	(-2, 6)	(-1, 0)	(0, 4)	(1, -6)	(2, -6)	(3, -4)	(4, 0)	(5, 6)

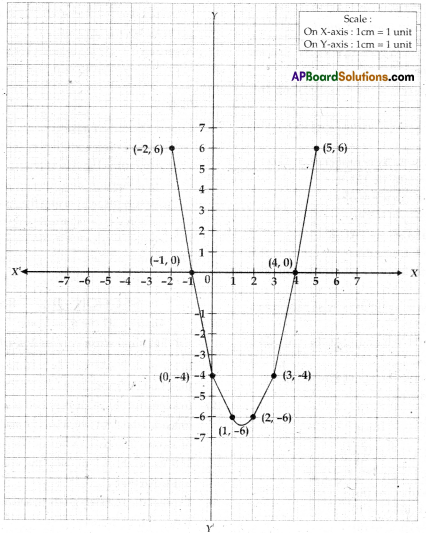
∴ The zeroes of the given polynomial are -1, and 4.