AP 10th Class Maths Model Paper Set 5 with Solutions

Regularly solving AP 10th Class Maths Model Papers Set 5 contributes to the development of problem-solving skills.

AP SSC Maths Model Paper Set 5 with Solutions

Instructions :

1. In the duration of 3 hours 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the answer booklet only.
3. Question paper consists of 4 Sections and 33 questions.
4. Internal choice is available in section – IV only.
5. Answers shall be written neatly and legibly.

Section – I
(12 × 1 = 12M)

Note:

1. Answer all the questions in one word or phrase.
2. Each question carries 1 mark.

Question 1.
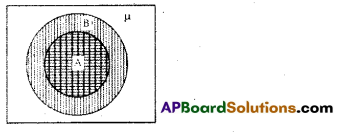
Draw Venn diagram if A ⊂ B then A ∩ B = A.
Solution:

Question 2.
What is the value of k for which the equations x + y – 4 = 0 and 2x + ky – 3 = 0 have no solution?
Solution:
\(\frac{1}{2}\) = \(\frac{1}{\mathrm{k}}\) ⇒ k = 2

Question 3.
Match the following.

A) a – i, b – ii, c – i
B) a – ii, b – iii, c – i
C) a – iii, b – ii, c – i
D) a – i, b – iii, c – ii
Solution:
D) a – i, b – iii, c – ii

Question 4.
Find the A.M of a – 2, a, a + 2.
Solution:
Arithmetic Mean

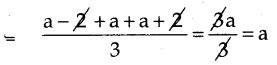
Question 5.
The angle of depression from the top of a tower 12 m height, at a point on the ground is 30°. The
distance of the point from the top is ……….
A) 12 m
B) 12 \(\sqrt{3}\) m
C) 7. 5 m
D) 6 m
Solution:
A) 12 m

Question 6.
Check whether -3 and 3 are the zeroes of the polynomial x² – 9.
Solution:
p(x) = x² – 9 ⇒ p(-3)
= (-3)² – 9 = 9 – 9 = 0
p(3) = (3)² – 9 = 9- 9 = 0
p(-3) = 0 and p(3) = 0
-3 and 3 are the zeroes of the polynomial
p(x) = x² – 9.

Question 7.
If one root of the equation x² + kx + 3 = 0 is 1 then find the other root.
Solution:
3

Question 8.
Draw a rough sketch of the combination of cone and hemisphere.
Solution:

Question 9.
The probability of picking a letter from the set of English alphabet is \(\frac{5}{26}\), then what are those alphabet ?
Solution:
Vowels [a, e, i, o, u]

Question 10.
Statement (A): Opposite sides are equal
Statement (B): Diagonals are not equal.
Which of the following is true considering both the statements ?
A) Square
B) Rhombus
C) Parallelogram
D) Rectangle
Solution:
D) Rectangle

Question 11.
Find the value of cosθ in terms of sinθ.
Solution:
sin²θ + cos²θ = 1
cos²θ = 1 – sin²θ
cosθ = \(\sqrt{1-\sin ^2 \theta}\).

Question 12.
Diagonal of a square is how many times of its side ?
Solution:
Diagonal (d) = \(\sqrt{2}\) × side

Section – II
(8 × 2 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 2 marks.

Question 13.
If A = {Prime numbers less than 10} and
B = {Positive odd numbers less than 10}, then find
i) A∩B
ii) B – A.
Solution:
A = {2, 3, 5, 7}
B = {1, 3, 5,7, 9}
A∩B = {2, 3, 5, 7} ∩ {1, 3, 5, 7, 9} = {3, 5, 7}
B – A = {1, 3, 5, 7, 9} – {2, 3, 5, 7} = {1, 9}

Question 14.
Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solution:
7 × 11 × 13 + 13 × 1 = 13 × [7 × 11 + 1]
= 13 × [77 + 1]
= 13 × 78
= 13 × 2 × 39
= 13 × 2 × 3 × 13
So, 7 × 11 × 13 + 13 is a composite number.
5 is a factor in the first term is in 7 × 6 × 5 × 4 × 3 × 2 × 1
∴ 5 is a factor in the second term i.e., 5
∴ 5 is a factor of both the numbers.
∴ 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 is a composite number.

Question 15.
Two concentric circles having radii 5 cm and 3 cm are drawn. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
As shown in the figure OP = 3 cm, OB = 5 cm
Since AB touches the smaller circle at P,
We have OP ⊥ AB
⇒ ∠OPB = 90° .

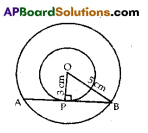
∴ By Pythagoras theorem,
OB² = OP² + PB²
⇒ PB² = OB² – OP²
⇒ 5² – 3² = 25 – 9 = 16
∴ PB = \(\sqrt{16}\) = 4 cm
Since the perpendicular through the centre bisects a chord
we have AP = PB = 4 cm
∴ AB = AP + PB = 4 cm + 4 cm = 8 cm
Thus, the length of the required chord = 8 cm.

Question 16.
Rajender observes a person standing on the ground from a helicopter at an angle of depression 45°. If the helicopter flies at a height of 50 meters from the ground, what is the distance of the person from Rajender?
Solution:
From the figure, in triangle OAB

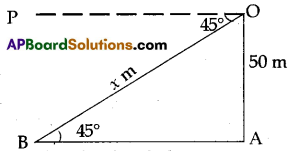
OA = height that helicopter flies from the ground 50 meters,
∠POB = ∠OBA = 45°
(Alternative interior angles)
distance of the person from Rajender = OB = x
sin 45° = \(\frac{\mathrm{OA}}{\mathrm{OB}}\) ⇒ x = 50\(\sqrt{2}\) m
The distance from the person to Rajender = 50\(\sqrt{2}\) m.

Question 17.
A page is opened at random from a book containing 100 pages. Find the probability that the page number is a perfect square.
Solution:
Number of pages of a book = 100
The list of perfect squares upto 100 is 1, 4, 9, 16, 25, 36, 49, 64, 81, 100
Let E be the event of getting a perfect square.
∴ E = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
Required probability = P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\)
= \(\frac{10}{100}\) = \(\frac{1}{10}\)

Question 18.
Find the distance between (a cos θ, 0) and (0, a sin θ).
Solution:

Question 19.
The perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.
Solution:
The perimeters of two similar triangles
= 30 cm, 20 cm
One side of first triangle = 12 cm
Let the corresponding side of the second triangle be x cm.
We know that
The ratio of perimeters of similar triangle = ratio of their corresponding sides.
⇒ \(\frac{30}{20}\) = \(\frac{12}{x}\)
⇒ x = 12 × \(\frac{20}{30}\) = 8
∴ The corresponding side of the second triangle = 8 cm.

Question 20.
Find a quadratic polynomial if the zeroes of it are 2 and \(\frac{-1}{3}\) respectively.
Solution:
Let the quadratic polynomial be ax² + bx + c, a ≠ 0 and its zeroes be α and β.
Here α = 2, β = \(\frac{-1}{3}\)
Sum of the zeroes = (α + β)
= 2 + \(\frac{-1}{3}\) = \(\frac{5}{3}\)
Product of the zeroes = αβ
= 2(\(\frac{-1}{3}\)) = \(\frac{-2}{3}\)
Therefore the quadratic polynomial
ax² + bx + c is k [x² – (α + β)x + αβ],
where k is a constant = k[x² – \(\frac{5}{3}\)x – \(\frac{2}{3}\)]
We can put different values of k.
When k = 3, the quadratic polynomial will be 3x² – 5x – 2.

Section – III
(8 × 4 = 32 M)

1. Answer all the questions,
2. Each question carries 4 marks.

Question 21.
Write two polynomials and create two questions for each of them.
Solution:
a) 2x² + 2x + 1 is a polynomial.

1. What is the sum of squares of two consecutive numbers ?
2. Find the length of one perpendicular side is 1 cm greater than the other, then the square of the hypotenuse is given by the polynomial 2x² + 2x + 1.

b) x² + 5x + 6 is also a polynomial.

1. A square is changed as a rectangle by enlarging two opposite sides by 2 units and the other pair by 3 units. To find the area of the rectangle, we get the given polynomial x² + 5x + 6.
2. In a family the age of father is 6 years greater than the sum of square of his son’s age and five times of his son’s age. White a polynomial for this situation.

Question 22.
The hypotenuse of a right triangle is 6m more than twice of the shortest side. If the third side is 2m less than the hypotensue, find the sides of the triangle.
Solution:
Let the shortest side be x m.
Then hypotensue = (2x + 6)m and third side
= (2x + 4)m.
by Pythagoras theorem, we have
(2x + 6)² = x² + (2x + 4)²
4x² + 24x + 36 = x² + 4x² + 16x + 6
x² – 8x – 20 = 0
(x – 10) (x + 2) = 0
x = 10 or x = -2
but x can’t be negative as side of a triangle.
∴ x = 10
Hence, the sides of the triangle are 10m, 26m, 24m.

Question 23.
The altitude of a right triangle is 7 cm less than its base. If the hypotenuse is 13 cm, find the other two sides.
Solution:
Let the base of the right triangle is x cm
Its altitude is 7cm less than its base
∴ Altitude is (x – 7) cm
Hypotenuse = 13 cm

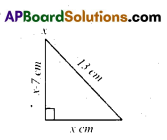
In a right angle triangle
(Hypotenuse)² = (side)² + (side)²
(13)² = x² + (x – 7)²
x² + x² – 14x + 49 = 149
2x² – 14x – 120 = 0
x² – 7x – 60 = 0
x² – 12x +5x – 60 = 0
x(x – 12) + 5 (x – 12) = 0
(x – 12) (x + 5) = 0
x – 12 = 0 or x + 5 = 0
x = 12 (or) x = – 5
Base of triangle can’t be negative
∴ Base of the triangle = 12 cm
Altitude of the triangle = 12 – 7 = 5 cm
∴ Other two sides are 5 cm and 12 cm.

Question 24.
Find the mode of the following data.
a) 5, 6, 9, 10, 6, 12, 3, 6, 11, 10, 4, 6, 7
b) 20, 3, 7, 13, 3, 4, 6, 7, 19, 15, 7, 18, 3
Solution:
a) Arranging the observations in order
3, 4, 5, 6, 6, 6, 6, 7, 9, 10, 10, 11, 12
6 is repeated maximum number of times.
So, mode = 6

b) Arranging the observations in order
3, 3, 3, 4, 6, 7, 7, 7, 13, 15, 18, 19, 20
3 and 7 are repeated maximum number of times (3)
So, modes are 3 and 7.

Question 25.
Find the point on X – axis, which is equidistant from (2, -5) and (-2, 9).
Solution:
Let P (x, 0) be the point on X – axis which is equidistant from A (2, – 5) and B (-2, 9)
PA = PB ⇒ PA² = PB²
⇒ (x – 2)² + (0 + 5)² = (x + 2)² + (0 – 9)²
⇒ x² – 4x + 4 + 25 = x² + 4x + 4 + 81
⇒ 4x + 4x = 25 – 81
⇒ 8x = -56
∴ x = \(\frac{-56}{8}\) = -7
Thus, the required point on X – axis = (-7, 0)

Question 26.
A toy is in the form of a cone mounted on a hemisphere. The diameter of the base and the height of the cone are 6 cm and 4 cm respectively. Determine the surface area of the toy. [use π = 3.14]
Solution:
Diameter of the cone (d) = 6 cm
Radius of the cone (r) = \(\frac{\mathrm{d}}{2}\) = \(\frac{6}{2}\) cm = 3 cm
Height of the cone (h) = 4 cm
Slant height (l) = \(\sqrt{\mathrm{r}^2+\mathrm{h}^2}\)
= \(\sqrt{3^2+4^2}\) = \(\sqrt{9+16}\)
= \(\sqrt{25}\) = 5cm

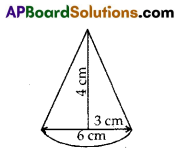
∴ Surface area of cone = πrl
= 3.14 × 3 × 5 cm² = 47.1 cm²
Surface area of hemisphere = 2πr² = 2 × 3.14 × 3 × 3 cm² = 56.52 cm²
Thus, total surface area of the toy
= SA of cone + SA of hemisphere
= 47.1 cm² + 56.52 cm²
= 103.62 cm²

Question 27.
If tan A = \(\frac{1}{\sqrt{3}}\) and tan B = \(\sqrt{3}\), then find sinA.cosB + cosA.sinB. (A, B < 90°).
Solution:
Given tan A = \(\frac{1}{\sqrt{3}}\) and tan B = \(\sqrt{3}\)
⇒ tan A = tan 30° and tan B = tan 60°
⇒ A = 30°, B = 60° [Since A, B are acute angles]
sin A . cos B + cos A . sin B
= sin 30°. cos 60° + cos 30° . sin 60°
= \(\frac{1}{2}\) × \(\frac{1}{2}\) + \(\frac{\sqrt{3}}{2}\) × \(\frac{\sqrt{3}}{2}\) = \(\frac{1}{4}\) + \(\frac{3}{4}\) = \(\frac{4}{4}\) = 1

Question 28.
How many two digit numbers are divisible by 3?
Solution:
The list of two digit numbers divisible by 3 is :
12, 15, 18,…. 99
It is in AP
Here, a = 12, d = 3, a_n = 99
As a_n = a + (n – 1)d,
we have 99 = 12 + (n – 1) × 3
i.e., 99 = 12 + 3n – 3 = 3n + 9
i.e., 3n = 99 – 9 = 90
i.e., n = \(\frac{90}{3}\) = 30
So, there are 30 two – digit numbers divisble by 3.

Section – IV
(5 × 8 = 40 M)

Note:

1. Answer all the questions.
2. Each question carries 8 marks,
3. Each question has internal choice.

Question 29.
Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9 m + 8.
(OR)
If A = {x : x is a natural number}
B = {x : x is an even natural number}
C = {x : x is an odd natural number}
D = {x : x is a prime number}
Find A ∩ B, A ∩ C, A ∩ D, B ∩ C, B ∩ D, C ∩ D.
Solution:
Let ‘a’ be any positive integer.
We apply Euclid’s division lemma with a and b = 3
Since 0 ≤ r < 3 the possible remainders are 0, 1 and 2
That is ‘a’ can be 3p or 3p +1 or 3p + 2 where p is the quotient.
Now (3p)³ = 27p³ which can be written in the form 9m since 9 is divisible by 9.
Again (3p + 1)³ = 27p³ + 27p² + 9p + 1 = 9 (3p³ + 3p² + p) + 1
which can be written in the form 9m + 8. since 27p³ + 27p² + 9p is 9 (3p³ + 3p² + p) is divisible by 9.
Lastly (3p + 2)³ = 27p³ + 54p² + 36p + 8
= 9(3p³ + 6p² + 4p) + 8
which can be written in the form 9m + 8. Since 27p³ + 54p² + 36p
i.e., 9 (3p³ + 6p² + 4p) is divisible by 9. Therefore, the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.

(Or)

A = {x : x is a natural number}
= {1, 2, 3, 4 ……..}
B = {x : x is an even natural number}
= {2, 4, 6, 8 ………}
C = {x : x is an odd natural number}
= {1, 3, 5, 7 ……….}
D = {x : x is a prime number}
= {2, 3, 5, 7, ……….}
The common elements in both sets.
A∩B = {2, 4, 6, 8 ………}
= {even natural numbers}
A∩C = {1, 3, 5, 7 ……..}
= {odd natural numbers}
A∩D = {2, 3, 5, 7 …….}
= {Prime numbers}
B∩ C = { } = φ
B∩D = {2} = φ
C∩D = {3, 5, 7 ……}
= {odd prime numbers}

Question 30.
A statue stands on the top of a 2m tall pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the statue.
(OR)
Rahim takes out all the hearts from the cards : What is the probability of
i. Picking out an ace from the remaining pack.
ii. Picking out a diamond
iii. Picking out a card that is not a heart.
iv. Picking out the Ace of heart.
Solution:
Height of the pedestal AB = 2 m
Let height of the statue AC = h meters

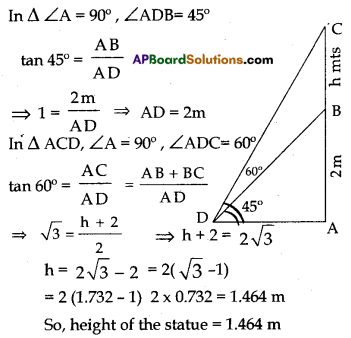
(Or)

Here, the sample space is the pack of cards.
n(S) = Total number of cards = 52.
All of the hearts in the cards = 13
Remaining pack = 52 – 13 = 39

i) Probability of picking out an ace
\(=\frac{\text { No.of aces in remaining pack }}{\text { Total no.of cards in remaining pack }}\) = \(\frac{3}{39}\) = \(\frac{1}{13}\)

ii) Probability of packing out a diamond
\(=\frac{\text { No.of diam onds in remaining pack }}{\text { Total no.of cards in remaining pack }}\)
\(\frac{13}{39}\) = \(\frac{1}{3}\)

iii) Probability of picking out a card that is not a heart.
\(=\frac{\text { No.of cards that is not a heart in remaining pack }}{\text { Total no.of cards in remaining pack }}\)
= \(\frac{39}{39}\) = 1

iv) Probability of picking out the ace of heart
\(=\frac{\text { No.of ace of heart in remaining pack }}{\text { Total no.of cards in remaining pack }}\)
= \(\frac{0}{39}\) = 0

Question 31.
A 20m deep well with diameter 7 m. is dug and the earth from digging is evenly spread out to form a platform 22 m. x 14 m. Find the height of the platform.
(OR)
If cosecθ + cotθ = k then prove that cosθ = \(\frac{k^2-1}{k^2+1}\)
Solution:
Diameter of well (d) = 7 m
∴ Radius of well (r) = \(\frac{d}{2}\) = \(\frac{7}{2}\) = 3.5 m
Height of the well (h) = 20m
Length of platform (l) = 22m
Breadth of platform (b) = 14m
Let the height of platform be H
According to the data, we note that
Volume of well = Volume of earth dug out

(Or)

Suppose cosecθ + cotθ = k …… (1)
we have, cosec²θ – cot²θ = 1
⇒ (cosecθ + cotθ) (cosecθ – cotθ) = 1
⇒ k(cosecθ – cotθ) = 1.
⇒ (cosecθ – cotθ) = \(\frac{1}{k}\) ……. (2)
Adding (1) and (2) we get
cosecθ + cotθ + cosecθ – cotθ = k + \(\frac{1}{\mathrm{k}}\)
⇒ 2 cosecθ = k + \(\frac{1}{\mathrm{k}}\) ………. (3)
Subtracting (1) and (2) we get

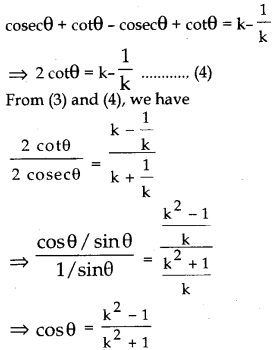
Question 32.
PQR is a triangle right angled at P and M is a point on QR such that PM ^ QR. Show that PM² = QR. MR.
(OR)
The following distribution gives the daily income of 50 workers of a factory.

Daily income (in Rupees )	250-300	300-350	350-400	400-450	450-500
Number of workers	12	14	8	6	10

Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.
Solution:
Given : In ∆PQR, ∠P = 90° and PM ⊥ QR
To prove : PM² = QM. MR
Proof: In ∆PQR ND ∆MPR, we have
∠R = ∠MRP [common angle]
∠P = ∠PMR = 90° [given]
∴ ∆PQR ~ ∆MPR …….. (1)
[By AA criterion of similarity]

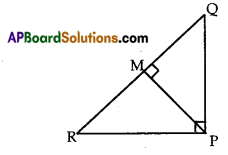
Similarly we can prove
∆PQR ~ ∆MQP …… (2)
From (1) and (2), we get
∆MPR ~ ∆MQP
The ratio of corresponding sides of similar triangles are equal
⇒ \(\frac{\mathrm{PM}}{\mathrm{MR}}\) = \(\frac{\mathrm{QM}}{\mathrm{PM}}\)
⇒ PM² = QM.MR
Hence the proof.

(Or)

Table for a less than type cumulative frequency distribution.

Upper limits	fr	Ascending cumulative for frequency		Suitable points
300	12	12	12	(300,12)
350	14	26	(12 + 14 =) 26	(350, 26)
400	8	34	(26+8 =)    34	(400,34)
450	6	40	(34+6 =)    40	(450,40)
500	10	50	(40+10 =) 50	(500,50)

Steps to draw less than ogive:

(a) Take the upper limits of the classes on X-axis and Ascending cumulative frequency number of workers on the Y-axis.
(b) Spot the corresponding suitable points on the coordinate plane and join the points.
(c) The smooth curve thus obtained by joining the points is the required less than type ogive.

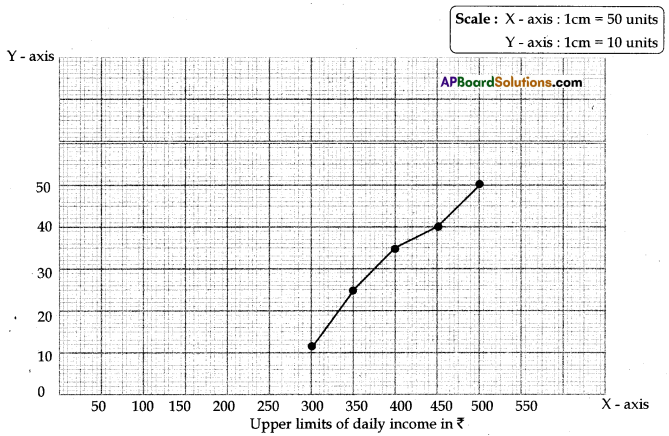
Question 33.
Solve the equations
2x – y = 4; 4x – 2y = 6 graphically.
(OR)
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle.
Solution:
2x – y = 4; 4x – 2y = 6

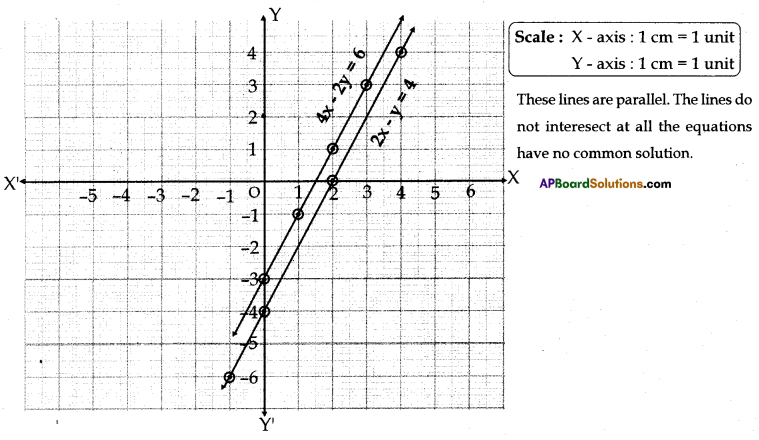
(Or)

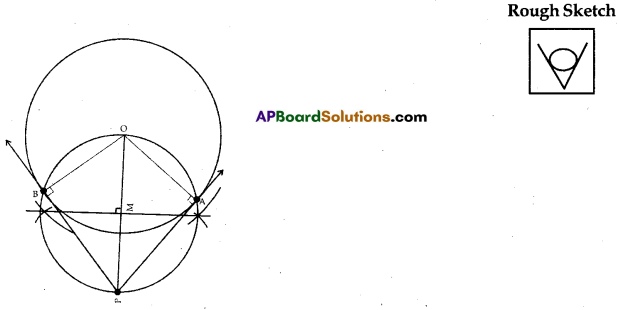
Construction:

1. Draw a circle of radius 6 cm. Let its centre be ‘O’
2. Let a point P be at a distance of 10 cm from the centre ‘O’
3. Join PO and draw the perpendicular bisector of PO which cuts it at the mid point M.
4. Taking M as centre, with radius PM or MO, we draw a circle that intersects the given circle at two points A and B.
5. Join PA and PB. These are the required tangents of the circle.