AP 10th Class Maths Model Paper Set 3 with Solutions

Regularly solving AP 10th Class Maths Model Papers Set 3 contributes to the development of problem-solving skills.

AP SSC Maths Model Paper Set 3 with Solutions

Instructions :

1. In the duration of 3 hours 15 minutes, 15 minutes of time is allotted to read the question paper.
2. All answers shall be written in the answer booklet only.
3. Question paper consists of 4 Sections and 33 questions.
4. Internal choice is available in section – IV only.
5. Answers shall be written neatly and legibly.

Section – I
(12 × 1 = 12M)

Note:

1. Answer all the questions in one word or a phrase.
2. Each question carries 1 mark.

Question 1.
If x² + 3x + k = 0 has equal roots, then what is the value of k?
Solution:
3² = 4(1)(k) ⇒ k = \(\frac{9}{4}\)

Question 2.
The decimal expansion of 0.225 in its rational form is
A) 225
B) \(\frac{225}{10^2}\)
C) \(\frac{225}{10^4}\)
D) \(\frac{9}{40}\)
Solution:
D) \(\frac{9}{40}\)

Question 3.
Choose the correct matching:
If α, β, γ are the zeros of a cubic polynomial ax³ + bx² + cx + d (a ≠ 0) then

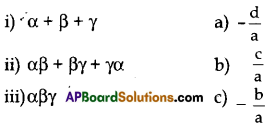
A) (i) – c, (ii) – b(iii) – a
B) (i) – a, (ii) – b, (iii) – c
C) (i) – b, (ii) – a, (iii) – c
D) (i) – b, (ii) – c, (iii) -a
Solution:
A) (i) – c, (ii) – b(iii) – a

Question 4.
Choose the correct matching:

a) {x : x is a multiple of 2}	i) Empty set
b) {x : x ∈ N and x < 1}	ii) Singleton set
c) {x : x is a even prime}	iii) Infinite set

A) a – i, b – ii, c – iii
B) a – iii, b – i, c – ii
C) a – ii, b – i, c – iii
D) a – iii, b – ii, c – i
Solution:
B) a – iii, b – i, c – ii

Question 5.
If x + y = 6, x – y = 10 then find ‘y’.
Solution:

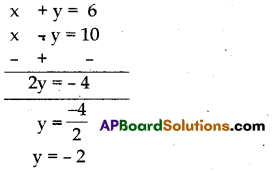
Question 6.
Name any objects which is in the shape of a cone.
Solution:
Ice cream cone, rice heap, tent etc.

Question 7.
In the given figure, P, Q are the mid points of sides XY and XZ, what is the relation between PQ and YZ?

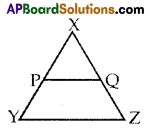
Solution:
PQ || YZ and PQ = \(\frac{1}{2}\) YZ.

Question 8.
If the common difference of A.P. is 2, then a₁₀ – a₅ =
A) 5
B) 10
C) 2
D) 20
Solution:
B) 10

Question 9.
Find the angle made by the minute hand in a clock during a period of 20 minutes.
Solution:
The angle made by minute hand to complete one complete rotation is = 360°
The angle made by minute hand in 60 min = 360°
The angle made by minute hand in

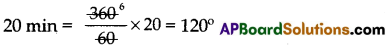
Question 10.
Define an angle of depression. Draw an angle of depression.
Solution:
Angle of depression: The angle of depression of an object viewed, is the angle formed by the line of sight with the horizontal level, i.e., the ease when we lower our head to look at the object.

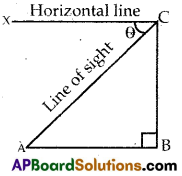
Question 11.
In the given figure ∠APB = 80° then find ∠AOB.

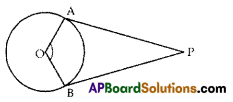
Solution:
From AOBP quadrilateral
∠A + ∠AOB + ∠B + ∠APB = 360°
90° + ∠AOB + 90° + 80° = 360°
∠AOB + 260° = 360°
∠AOB = 360 – 260
∠AOB = 100°

Question 12.
Which of the following is the modal class for the following data?

C.I	0-10	10-20	20-30	30-40	40-50
f	7	13	25	3	2

Solution:
Modal class is 20 – 30

Section – II
(8 × 2 = 16 M)

Note:

1. Answer all the questions.
2. Each question carries 2 marks.

Question 13.
Find the median of the ungrouped data 2, 12, 7, 5, 10, 6 ?
Solution:
Given data : 2,12, 7,5,10, 6
Writing in ascending order : 2, 5, 6, 7,10, 12
Number of observations (n) = 6 (an even number)
∴ Median = Average of \(\left(\frac{\mathrm{n}}{2}\right)^{\mathrm{th}}\) and \(\left(\frac{\mathrm{n}}{2}+1\right)^{\mathrm{th}}\) observations.
= Average of 3^rd and 4^th observations.
= Average of 6 and 7 = \(\frac{6+7}{2}\) = 6.5

Question 14.
Find the LCM and HCF of 324 and 360.
Solution:
We have 324 = 2 × 2 × 3 × 3 × 3 × 3 = 2² × 3⁴
360 = 2 × 2 × 2 × 3 × 3 × 5 = 2³ × 3² × 5¹
LCM (324, 360) = 3⁴ × 2³ × 5¹ = 3240
HCF (324, 360) = 2² × 3² = 4 × 9 = 36

Question 15.
Find the sum and product of roots of the quadratic polynomial x² – 4\(\sqrt{3}\)x + 9 = 0.
Solution:
Given quadratic equation is = x² – 4\(\sqrt{3}\)x + 9 = 0
Sum of roots (α + β) = \(\frac{-b}{a}\) = \(\frac{-(-4 \sqrt{3})}{1}\) = 4\(\sqrt{3}\)
Product of roots (αβ) = \(\frac{c}{a}\) = \(\frac{9}{1}\) = 9.

Question 16.
Find the probability that there are 53 Sundays in a leap year.
Solution:
A leap year contains 52 weeks and 2 days.
So, 52 Sundays are guaranteed and for our event one of the two days should be Sunday.
S = {(Sun, Mon), (Mon, Tue), (Tue, Wed), (Wed, Thu), (Thu, Fri), (Fri, Sat), (Sat, Sun)}
Out of all the 7 possible outcomes only 2 outcomes (Sun, Mon) and (Sat, Sim) will favour our event.
So, required probability = \(\frac{2}{7}\)

Question 17.
Find the volume and surface area of a sphere of radius 2.1 cm (π = \(\frac{22}{7}\))
Solution:

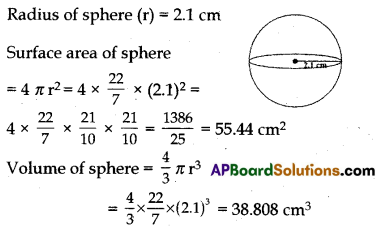
Question 18.
Find the slope of AB with given end points (-a, a) and (0, a + a\(\sqrt{3}\)).
Solution:
Points of a line are (-a, a) and (0, a + a\(\sqrt{3}\))
The slope of the line m = \(\frac{y_2-y_1}{x_2-x_1}\)
= \(\frac{(a+a \sqrt{3})-a}{0-(-a)}\) = \(\frac{a+a \sqrt{3}-a}{a}\) = \(\frac{a \sqrt{3}}{a}\) = \(\sqrt{3}\)
∴ Slope of the given line is \(\sqrt{3}\).

Question 19.
Calculate the length of tangent from a point 15 cm away from the centre of a circle of radius 9 cm.
Solution:
It is given that radius (r) = 9 cm
OQ (d) = 15 cm

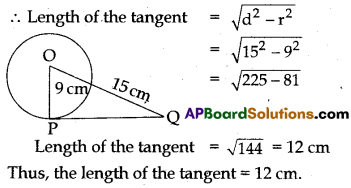
Question 20.
In ∆ABC, DE||BC and \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{3}{5}\). AC = 5.6. Find AE.
Solution:

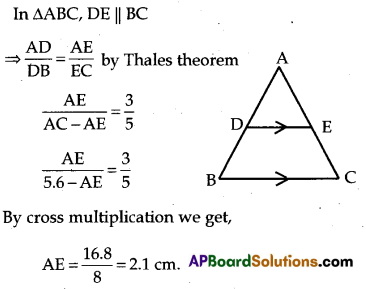
SECTION – III
(8 × 4 = 32 M)

Note:

1. Answer all the questions.
2. Each question carries 4 marks.

Question 21.
Find two numbers whose sum is 27 and product is 182.
Solution:
Sum of two numbers = 27
Let one number be x
Second number = 27 – x ………. (1)
Product = 182 …… (2)
x(27 – x) = 182
27x – x² = 182
27x – x² – 182 = 0
x² – 27x + 182 = 0
x² – 13x – 14x + 182 = 0
x(x -13) – 14 (x – 13) = 0
(x – 13)(x – 14) = 0
x -13 = 0 or x -14 = 0
x – 13 = 0 gives x = 13
If first number is 13 second number = 27 – 13 = 14
x – 14 = 0 gives x = 14
If first number is 14, second number = 27 – 14 = 13
Therefore two numbers are 13 and 14.

Question 22.
If x² + y² = 25xy then prove that 2 log (x + y) = 3 log 3 + log x + log y.
Solution:
Given x² + y² = 25xy
Adding 2xy both sides
x² + y² + 2xy = 25xy + 2xy
log (x + y)² = 27xy
Taking ‘log’ on both sides
log (x + y)² = log (27xy)
We know that
log_axⁿ = nlog_ax
2 log(x + y) = log 27 + log x + log y
log_axyz = log_ax + log_ay + log_az
27 = 9 × 3 = 3 × 3 × 3 = 3³
2log(x + y) = log 3³ + log x + log y
2log(x + y) = 3 log 3 + log x + log y

Question 23.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and – 2x + 4, respectively. Find g(x).
Solution:
Given polynomial is x³ – 3x² + x + 2
Dividing this polynomial by g(x)
Quotient = x – 2 and Remainder = -2x + 4
By division algorithm

Question 24.
Show that tan²θ + tan⁴θ = sec⁴θ – sec²θ.
Solution:
LHS = tan²θ + tan⁴θ = tan²θ (1 + tan²θ)
= tan²θ . sec²θ [∵ sec²θ – tan²θ = 1]
= (sec²θ – 1) . sec²θ = sec⁴θ – sec²θ = RHS

Question 25.
A solid iron rod has a cylindrical shape. Its height is 11 cm. and base diameter is 7 cm. Then find the total volume of 50 rods?
Solution:
Height of cylindrical rod (h) = 11 cm
Base diameter of it (d) = 7 cm
∴ Its radius (r) = \(\frac{d}{2}\) = \(\frac{7}{2}\) cm
Volume of the rod = πr²h
= \(\frac{22}{7}\) × \(\frac{7}{2}\) × \(\frac{7}{2}\) × 11 cm³ = \(\frac{847}{2}\) cm³
Total volume of 50 such rods 847
= 50 × \(\frac{847}{2}\) cm³ = 25 × 847 cm³ = 21175 cm³

Question 26.
A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increases uniformly by a fixed number every year. Find :
i) the production in the 1^st year
ii) the production in the 10^th year
Solution:
i) Since the production increases uniformly by a fixed number every year, the number of TV sets manufactured in 1^st, 2^nd, 3^rd, . . . , years will form an AP.
In AP,

Substitute the value of d in equation (1)
a + 2(25) = 600
a + 50 = 600
a = 600 – 50 = 550

ii) Now,
a₁₀ = a + 9d = 550 + 9 × 25 = 550 + 225 = 775
So, production of TV sets in the 10^th year is 775.

Question 27.
Solve \(\frac{2}{x}\) + \(\frac{3}{y}\) = 13; \(\frac{5}{x}\) – \(\frac{4}{y}\) = -2 where x ≠ 0 ; y ≠ 0 by reducing them to a pair of linear equations
Solution:
2\(\left(\frac{1}{x}\right)\) + 3\(\left(\frac{1}{y}\right)\) = 13 ……… (1)
5\(\left(\frac{1}{x}\right)\) – 4\(\left(\frac{1}{y}\right)\) = 13 ……… (2)
If we substitute \(\left(\frac{1}{x}\right)\) = p and \(\left(\frac{1}{y}\right)\) = q we get a pair of linear equations :
2 p + 3 q = 13
5 p – 4 q = -2
Elimination Method:

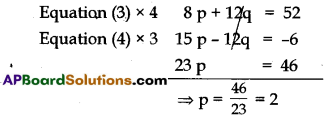
Substitute the value of p in (3)
2 (2) + 3q = 13
4 + 3q = 13
3q = 13 – 4
3q = 9
∴ q = \(\frac{9}{3}\) = 3
But \(\left(\frac{1}{x}\right)\) = p ⇒ \(\left(\frac{1}{x}\right)\) = 2 ⇒ x = \(\frac{1}{2}\)
\(\left(\frac{1}{y}\right)\) = q ⇒ \(\left(\frac{1}{y}\right)\) = 2 ⇒ y = \(\frac{1}{3}\)

Question 28.
AB, CD, PQ are perpendicular to BD. AB = x, CD = y and PQ = z prove that \(\frac{1}{x}\) + \(\frac{1}{y}\) = \(\frac{1}{z}\)

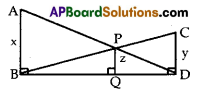
Solution:
Given: AB, CD, PQ are perpendicular to BD.
AB = x, CD= y and PQ = z
To prove: \(\left(\frac{1}{x}\right)\) + \(\left(\frac{1}{y}\right)\) = \(\left(\frac{1}{z}\right)\)
Proof: In ∆PQB and ∆CDB we have
∠PQB = ∠CDB = 90 [given]
∠B = ∠B [common angle]
∴ By AA criterion of similarity, ∆PQB ~ ∆CDB

Section – IV
[5 × 8 = 40 M]

Note:

1. Answer all the questions.
2. Each question carries 8 marks,
3. Each question has internal choice.

Question 29.
Prove that \(\sqrt{2}\) + \(\sqrt{3}\) is irrational.
(OR)
i) Is the empty set subset to every set ?
ii) Is any set subset to itself ?
iii) You are given two sets such that a set is not a subject of the other. If you have to prove this how do you prove ? Justify your answers.
Solution:
Let us suppose that \(\sqrt{2}\) + \(\sqrt{3}\) is rational.
Let \(\sqrt{2}\) + \(\sqrt{3}\) = \(\frac{a}{b}\), where a, b are integers and b ≠ 0
Therefore,
Squaring on both sides, we get

Since a, b are integers, \(\frac{a^2+b^2}{2 a b}\) is rational, and so, \(\sqrt{3}\) is irrational.
This contradicts the fact that \(\sqrt{3}\) is irrational.
Hence, \(\sqrt{2}\) + \(\sqrt{3}\) is irrational.

(OR)

i) Yes, empty set is subset to everyset.
ii) Yes. Every set is subset to itself.
iii) If A and B are any two sets such that A ⊊ B orB ⊆ B.
To prove A ⊊ B.
It is enough to prove that there exists at least one element in A which is not present in B. i.e., Ex: x ∈ A and x ∈ B
Similarly to prove B ⊊ A
It is enough to prove that there exists at least one element in B which is not present in A.
i.e. Ex: x ∈ B and x ∉ A

Question 30.
If (1, 2), (4, y), (x, 6), (3, 5) are the vertices of a parallelogram taken in order, find x and y.
(OR)
AB and CD are respectively area of two concentric circles of radii 21 cm and 7 cm. with centre O (See figure). If ∠AOB = 30°, find the area of the shaded region.

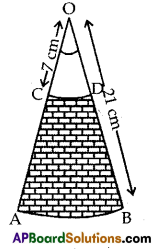
(use π = \(\frac{22}{7}\))
Solution:
Let the points A(1, 2), B(4, y), C(x, 6) and D(3, 5) are the vertices of a parallelogram ABCD.

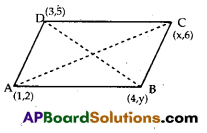
We know that, “The diagonals of a parallelogram bisect each other.”
So, the mid points of the diagonals AC and DB are equal.

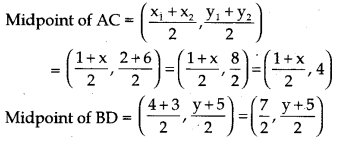
(OR)

Question 31.
i) Show that sec²θ + cosec²θ = sec²θ.cosec²θ.
ii) Prove that \(\sqrt{\frac{1+\cos \theta}{1-\cos \theta}}\) = cosec θ + cot θ.
(OR)
A die is thrown once. Find the probability of getting
i) a prime number;
ii) a number lying between 2 and 6;
iii) an odd number.
Solution:
i)

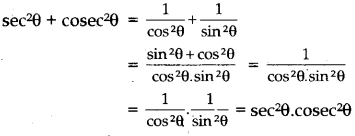
ii)

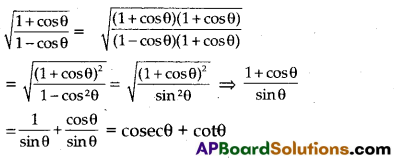
(OR)

When a die is thrown, sample space S = {1, 2, 3, 4, 5, 6}

i) Let A denotes the event of getting a prime number. Then A = {2, 3, 5}
So, required probability = P(A)
= \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)
ii) Let B denote the event of getting a number between 2 and 6.
Then, B = {3,4,5}
∴ Required probability = P(B)
= \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

iii) Let C denotes the event of getting an odd number. Then C = {1, 3, 5}
So, required probability, P(C)
= \(\frac{n(C)}{n(S)}\) = \(\frac{3}{6}\) = \(\frac{1}{2}\)

Question 32.
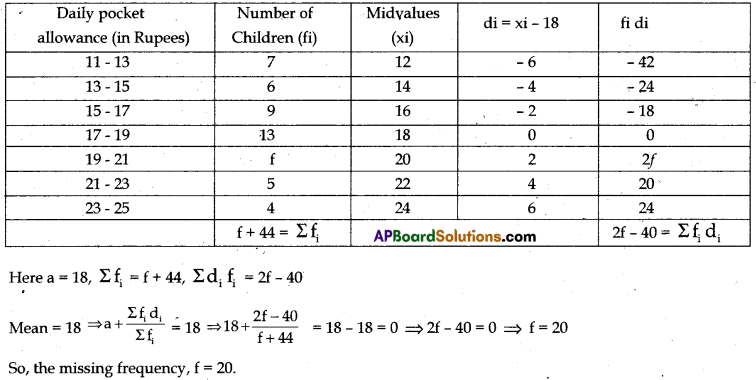
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is ₹ 18. Find the missing frequency f.

Daily pocket allowance(in Rupees)	11-13	13-15	15-17	17-19	19-21	21-23	23-25
Number of children	7	6	9	13	/	5	4

(OR)

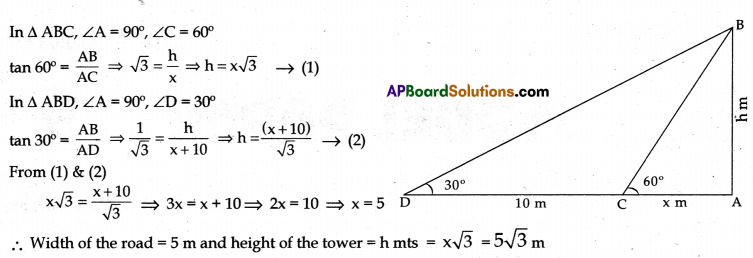
A TV tower stands vertically on the side of a road. From a point on the other side directly opposite to the tower, the angle of elevation of the top of tower is 60°. From another point 10m away from this point, on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and width of the road.
Solution:
Given that, mean pocket allowance is ₹ 18.
We will find the mean of the given data and equalize it with 18 to find the value of’/’.

(OR)

Let AC = x mts = width of the road and AB = h mts = height of the tower
Distance between points C and D = CD = 10m

Question 33.
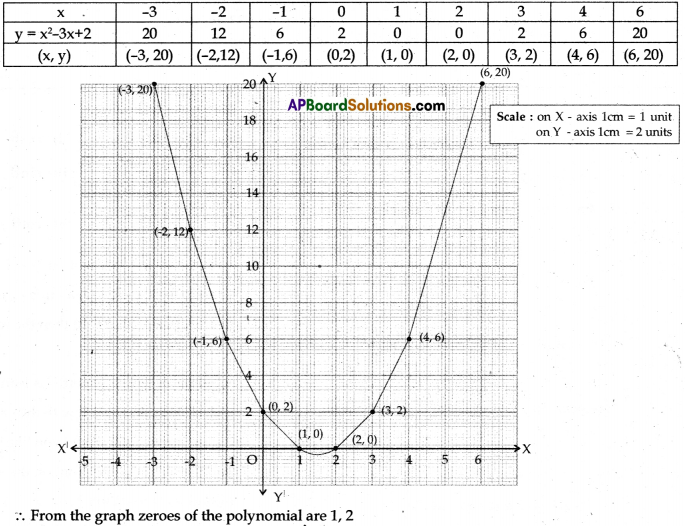
Draw the graph of polynomial p(x) = x² – 3x + 2 and find its zeroes from the graph.
(OR)
Construct an Isosceles triangle whose base is 8 cm and altitude is 4 cm. Then, draw another triangle whose sides are 1\(\frac{1}{2}\) times the corresponding sides of the isosceles triangle.
Solution:
Let p(x) = x² – 3x + 2 = y

(OR)

Steps of construction:

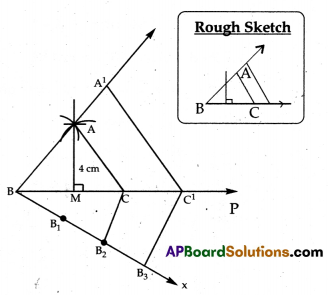
1. Construct an isosceles triangle ABC with the given measurements.
2. Draw a ray BX making an acute angle with BC on the opposite side of A.
3. Locate 3 points B₁/B₂/B₃,on BX so that BB₁ = B₁B₂ = B₂B₃.
4. Produce BC upto P
5. Join B₂C and draw a line from B₃ to C¹ which is parallel to B₂C and it is intersecting BP at C¹.
6. Draw a line through C¹ parallel to CA to intersect the produced line of BA at A¹
∴ A ‘BC’ is the required triangle.