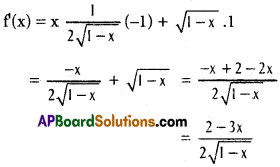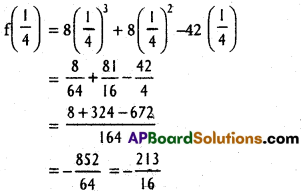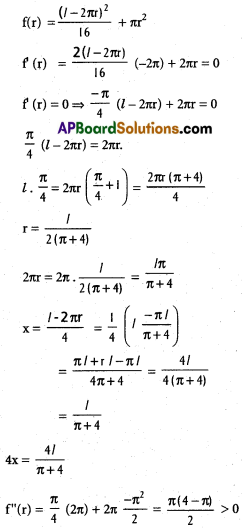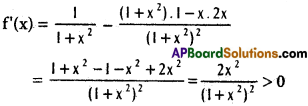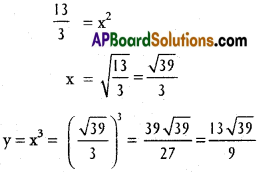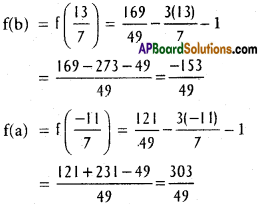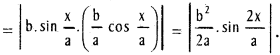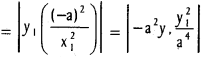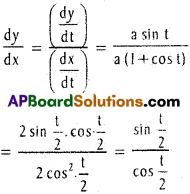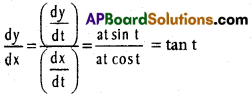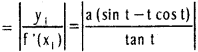Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(h) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(h)
I.
Question 1.
Find the points of local extrema (if any) and local extrema of the following functions each of whose domain is shown against the function.
i) f(x) – x², ∀ x ∈ R.
Solution:
f(x) = x²
f'(x) = 2x ⇒ f”(x) = 2
For maximum or minimum f'(x) = 0
2x = 0
x = 0
Now f”(x) = 2 > 0 ,
∴ f(x) has minimum at x = 0
Point of local minimum x = 0
Local minimum = 0.
ii) f(x) = sin x, [0, 4π)
Solution:
Given f(x) = sinx
⇒ f'(x) = cosx
⇒ f”(x) = -sinx
For max on min,
f'(x) = 0
cos x = 0
⇒ x = \(\frac{\pi}{2},\frac{3\pi}{2},\frac{5\pi}{2},\frac{7\pi}{2}\)
i) f”(\(\frac{\pi}{2}\)) = -sin\(\frac{\pi}{2}\) = -1 < 0
f(x) = sin \(\frac{\pi}{2}\) = 1
∴ Point of local maximum x = \(\frac{\pi}{2}\)
local maximum – 1
ii) f”(\(\frac{3\pi}{2}\)) = – sin \(\frac{3\pi}{2}\) = -1 > 0
f(x) = sin \(\frac{3\pi}{2}\) = -1
∴ Point of local minimum x = \(\frac{3\pi}{2}\)
local minimum x = -1
iii) f”(\(\frac{5\pi}{2}\)) = – sin \(\frac{5\pi}{2}\) = -1 > 0
f(x) = sin \(\frac{5\pi}{2}\) = 1
∴ Point of local maximum x = \(\frac{5\pi}{2}\)
local maximum = 1
iv) f”(\(\frac{7\pi}{2}\)) = – sin \(\frac{7\pi}{2}\) = -1 > 0
f(x) = sin \(\frac{7\pi}{2}\) = -1
∴ Point of local maximum x = \(\frac{7\pi}{2}\)
local maximum = 1

iii) f (x) = x³ – 6x² + 9x + 15 ∀ x ∈ R.
Solution:
f (x) = 3x² – 12x + 9 and f'(x) = 6x – 12
For maximum or minimum f(x) = 0
⇒ 3x² – 12x + 9 = 0
⇒ x² – 4x + 3 = 0
⇒ (x – 1) (x – 3) = 0
⇒ x = 1 or 3
Now f”(1) = 6(1) – 12 = – 6 < 0
∴ f(x) has maximum value at x = 1
Max. valueis f(1)= 1³ – 6(1)² + 9(1) + 15
= 1 – 6 + 9 + 15 = 19
f”(3) = 6(3) – 12 = 18 – 12 = 6 > 0
∴ f(x) has minimum value at x = 3
Min. value is f(3) = 33 – 6.32 + 9.3 + 15
= 27 – 54 + 27+ 15
= 15
iv) f(x) = \(\sqrt{1-x}\) ∀ x ∈ (0, 1)
Solution:
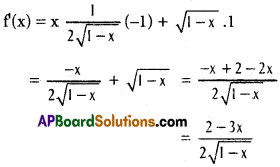
For max. or min. f'(x) = 0

v) f(x) = 1/x² + 2 ∀ x ∈ R
Solution:

∴ For maximum or minimum f (x) = 0
⇒ \(\frac{-2x}{(x^{2}+2)^{2}}\) = 0 ⇒ x = 0
f”(0) = \(\frac{2(0-2)}{(0+2^{3})}=\frac{-4}{8}=\frac{-1}{2}\) < 0
∴ f(x) has max. value at x = 0
Max. value is f(0) = \(\frac{1}{0+2}=\frac{1}{2}\)
vi) f(x) = x²- 3x ∀ x ∈ R
Solution:
f(x) = 3x² – 3 and f”(x) = 6x
∴ For maximum or minimum f(x) = 0
⇒ 3x² – 3 = 0
⇒ x² – 1 = 0
⇒ x = ± 1
Now f”(1) = 6(1) = 6 > 0
∴ f(x) has minimum at x = 1
Minimum value is f(1) = 1³ – 3(1) = -2
f”(-1) = 6(-1) = -6 < 0
∴ f(x) has maximum value at x = -1
Maximum value is f(-1) = (-1)³ – 3(-1)
= -1 + 3 = 2
vii) f(x) = (x -1) (x + 2)² ∀ x ∈ R
Solution:
f(x) = (x – 1) (x + 2)²
f(x) = (x – 1) 2(x + 2) + (x + 2)²
= 2(x – 1) (x + 2) + (x + 2)²
f”(x) = 2(x – 1) + 2(x + 2) + 2(x + 2)
= 2(3x + 3) = 6(x + 1)
∴ For maximum or minimum f'(x) = 0
2(x – 1) (x + 2) + (x + 2)² = 0
(x + 2) [2(x – 1) + (x + 2)] = 0
⇒ (x + 2) (3x) = 0
⇒ x = 0, x = -2
Now f”(0) = 6(0 + 1) = 6 > 0
∴ f(x) has min. value at x = 0
Min. value is f(0) = (0 – 1) (0 + 2)² = -4
f'(-2) = 6 (-2 + 1) = -6 < 0
∴ f(x) has max. value at x = -2
Max. value is f(-2) = (-2 -1) (-2 + 2)² = 0
viii) f(x) = \(\frac{x}{2}+\frac{2}{x}\) ∀ x ∈ (0, ∞)
Solution:
f'(x) = \(\frac{1}{2}-\frac{2}{x^{2}}\) and f”(x) = \(\frac{4}{x^{3}}\)
∴ For max. or min. f'(x) = 0
⇒ \(\frac{1}{2}-\frac{2}{x^{2}}\) = 0 ⇒ x² – 4 = 0 ⇒ x = ± 2
f”(2) = \(\frac{4}{2^{3}}\) = \(\frac{1}{2}\) > 0 (Since x > 0)
∴ f(x) has min. value at x = 2
Min. value is f(2) = \(\frac{2}{2}+\frac{2}{2}\) = 1 + 1 = 2.
ix) f(x) = – (x – 1)³ (x + 1)² ∀ x ∈ R
Solution:
f(x) = -(x – 1)³ (x + 1)² = (1 – x)³ (x + 1)²
f”(x) = (1 – x)³ 2(x + 1) + 3(1 – x)² (-1) (x + 1)²
= (1 – x)² (x + 1) {2(1 – x) – 3(x + 1)}
= (1 – x)² (x + 1) {2 – 2x – 3x – 3}
= (1 – x)² (x + 1) (-1 – 5x)
f”(x) = (1 – x)² (x + 1) (-5) + (1 – x)² (-1 – 5x) + (x + 1) (-1 -5x) 2(1 – x) (-1)
= -5 (1 -x)² (x+ 1) – (1 + 5x) (1 – x)² + (x + 1) (1 + 5x) 2(1 – x)
∴ For maximum or minimum f(x) = 0
(1 – x)² (x + 1) (-1 – 5x) = 0
⇒ x = ± 1 or -1/5
f”(1) = 0 – 0 + 0 ⇒ critical value at x = 0
f”(1 +1)² (-1) = 0 – (1 – 5) + 0 = 16 > 0
∴ f(x) has min. value at x = -1
Min. value = f(-1) = (1 + 1)³ (-1 + 1)² = 0
f”(- \(\frac{1}{5}\)) < o
⇒ f(x) has max. value at x = – \(\frac{1}{5}\)
Min. value is f (-\(\frac{1}{5}\)) = \(\frac{3456}{3125}\)
x) f(x) = x² e3x ∀ x ∈ R
Solution:
f'(x) = x² e3x .3 + e3x. 2x
For maximum or minimum f'(x) = 0
3x² e3x + 2e3x. x = 0
x² e3x (3x + 2) = 0
x = 0, x = \(\frac{-2}{3}\) and e = 0 is not possible
Now f”(x) = 3(x² e3x. 3 + e3x 2x)
+ e3x 2 + 2x e3x
f”(x) = 9x²e3x + 6x
e3x+ 2 e3x + 6xe3x
= 9x²e3x + 12xe3x + 2e3x
f”(0) = 2 > 0
∴ Point of local minimum = 0
local minimum = 0
f”(\(\frac{-2}{3}\)) = \(\frac{-2}{e^{2}}\) < 0
∴ point of local maximum = \(\frac{-2}{3}\)
local maximum = \(\frac{4}{9e^{2}}\)

Question 2.
Prove that the following functions do not have absoute maximum and absolute minimum.
i) ex in R
Solution:
f(x) = ex and f”(x) = ex
∴ For maxima or minima f'(x) = 0 ⇒ ex = 0
⇒ x value is not defined
Hence it has no maxima or minima.
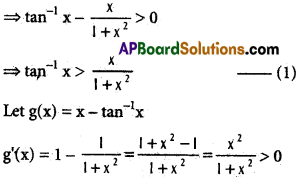
ii) log x in (0, ∞)
Solution:
f(x) = \(\frac{1}{x}\) and f”(x) = – \(\frac{1}{x^{2}}\)
f (x) = 0 ⇒ x value is not defined
⇒ f(x) has no maxima or minima.
iii) x³ + x² + x + 1 in R
Solution:
f (x) = 3x² + 2x + 1 gives imaginary values.
⇒ It has no maximum or minimum values.
II.
Question 1.
Find the absolute maximum value and absoulte minimum value of the following functions on the domain specified against the function.
Solution:
f(x) = x³ on (-2, 2)
f(x) = 3x² and f'(x) – 6x
the value f(-2) = (-2)³ = – 8
Max Value f(2) = 2³ = 8
ii) f(x) = (x – 1)²+ 3 on [-3, 1]
Solution:
f(x) = 2(x – 1) and f'(x) = 2
Max. value f(-3) = (-3 – 1)² + 3 = 16 + 3 = 19
Min. value f(l) = 0 + 3 = 3
iii) f(x) = 2|x| on [-1, 6]
Solution:
f'(x) = \(\frac{2|x|}{x}\)
For max. or min., f'(x) = 0
\(\frac{2|x|}{x}\) = 0 ⇒ x = 0
f(0) = 0
f(-1) – 2|-1| = 2
f(6) = 2(6) = 12
Absolute minimum = 0
Absolute maximum = 12
iv) f(x) = sin x + cos x on [0, π]
Solution:
f'(x) cos x – sin x which exists at all x ∈ (0, π)
Now f'(x) = 0 ⇒ cos x – sin x = 0
⇒ tan x = 1
⇒ x = \(\frac{\pi}{4}\) ∈ (0, π)
Now f(0) = sin 0 + cos 0 = 1
f(\(\frac{\pi}{4}\)) = sin \(\frac{\pi}{4}\) + cos \(\frac{\pi}{4}\)
= \(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)
f(π) = sin π + cos π = 0 – 1 = -1
∴ Minimum value : -1
Maximum value: √2
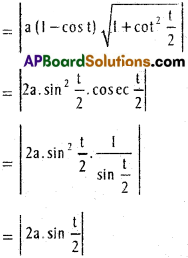
v) f(x) = x + sin 2x on [0, π]
Solution:
f(x) = x + sin 2x
f(x) = 1 + 2 cos 2x
f (x) = 0 ⇒ 2 cos 2x + 1 = 0
⇒ cos 2x = –\(\frac{1}{2}\) = cos \(\frac{2 \pi}{3}\)
⇒ 2x = \(\frac{2 \pi}{3}\)
⇒ x = \(\frac{\pi}{3}\) ∈ (0, 2π)
Now f(0) = 0 + sin 2(0) = 0
f(\(\frac{\pi}{3}\)) = \(\frac{\pi}{3}\) + sin 2.\(\frac{\pi}{3}\) = \(\frac{\pi}{3}+\frac{\sqrt{3}}{2}\)
f(2π) = 2π + sin 2. 2π = 2π + 0 = 2π
Minimum value = 0
Maximum value is = 2π
Question 2.
Use the first derivative test to find local extrema of f(x) = x³ – 12x on R.
Solution:
f(x) = x³ – 12x
f'(x) = 3x² – 12
f”(x) = 6x
For maximum or minimum, f'(x) = 0
3x² – 12 = 0
3x² = 12
x = ± 2
f”(2) = 12 > 0
Point of local minimum at x = 2
Local minimum = – 16
f”(-2) = -12 < 0
Point of local maximum at x = -1
Local maximum =16
Question 3.
Use the first derivative test to find local extrema of f(x) = x² – 6x + 8 on R.
Solution:
f(x) = x² – 6x + 8
f’(x) = 2x -6 ⇒ f”(x) = 2
For maximum or minimum f'(x) = 0
2x – 6 = 0
⇒ x = 3
f”(3) = 2 > 0
∴ Point of local minimum x = 3
Local minimum = -1

Question 4.
Use the second derivative test to find local extrema of the function
f(x) =x³ – 9x² – 48x + 72 on R.
Solution:
f(x) =x³ – 9x² – 48x + 72.
⇒ f'(x) = 3x² – 18x – 48
= 3(x – 8) (x + 2)
Thus the stationary point are – 2 & 8
f”(x) = 6x – 18 = 6(x – 3)
At x= 8, f”(8) = 30 > 0
∴ f (8) = (8)³ – 9(8)² – 48(8) + 72
= 512 – 576 – 384 + 72
= – 376
At x= -2, f”(-2) = – 30 < 0
f(-2) = (-2)³ – 9(-2)² – 48(-2)+72
= -8 – 36 + 96 + 72
= 124
Local minimum = -376
Local maximum = 124
Question 5.
Use the second derivative test to find local extrema of the function. f(x) = -x³ + 12x² – 5 on R.
Solution:
f(x) = -x³ + 12x² – 5
⇒ f'(x) = -3x² + 24x
= -3x(x – 8)
Thus the stationary point are 0, 8
f”(x) = – 6x + 24
At x= 0, f”(0) = 24 > 0.
f(0) = -5
At x= 8, f”(8) = -24 < 0
f(8) = -8³ + 12(8)² – 5
= -512 + 768 – 5 = 251
Local minimum = -5
Local maximum = 251
Question 6.
Find local maximum or local minimum of f(x) = -sin 2x – x defined on [-π/2, π/2].
Solution:
f(x) =-sin 2x – x
f'(x) = -2cos 2x – 1
f”(x) = 4 sin 2x
Thus the starting point are x = \(\frac{\pi}{3},\frac{-\pi}{3}\)

Local minimum = –\(\frac{\sqrt{3}}{2}-\frac{\pi}{3}\)
Local maximum = \(\frac{\sqrt{3}}{2}+\frac{\pi}{3}\)
Question 7.
Find the absolute maximum and absolute minimum of f (x) = 2x³ – 3x² – 36x + 2 on the interval [0, 5].
Solution:
f(x) = 2x³ – 3x² – 36x + 2
f(x) = 6x² – 6x – 36
f(x) = 12x – 6
for maxima or minima, f'(x) = 0
6x² – 6x – 36 = 0
x² – x – 6 = 0
x² -3x + 2x – 6 = 0
x(x – 3) + 2(x – 3) = 0
(x + 2) (x – 3) = 0
x = 3, -2
f”(3) = 30 > 0
f(x) has max/min value at x = 3
f(3) = 2(3)³ – 3(3)² – 36(3) + 2
= 54 – 27 – 108 + 2
= -79
Absolute minimum = – 79
Since 0 ≤ x ≤ 5
∴ f(0) = 0 – 0 – 0 + 2
= 2
∴ Absolute maximum = 2.

Question 8.
Find the absolute extremum of f(x) = 4x – \(\frac{x^{2}}{2}\) on [-2, \(\frac{9}{2}\)]
Solution:
f(x) = 4x – \(\frac{x^{2}}{2}\)
f'(x) =4 – x
f”(x) = – 1
for maxima or minima f'(x) = 0
4 – x = 0
x = 4
f”(4) = -1 < 0
∴ f has maximum value at x = 4
f(4) = 16 – \(\frac{16}{2}\) = 8
Since -2 ≤ x ≤ \(\frac{9}{2}\)
∴ f(-2) = -8 – \(\frac{4}{2}\)
= -8- 2 = -10
∴ Absolute minimum = -10
Absolute maximum = 8
Question 9.
Find the maximum profit that a company can make, if the profit function is given by P(x) = -41 + 72x – 18x²
Solution:
P(x) = – 41 + 72 x – 18x².
\(\frac{dp(x)}{dx}\) = 72 – 36x
for maxima or minima, \(\frac{dp}{dx}\) = 0
72 – 36x = 0
x = 2
\(\frac{d^{2}p}{dx^{2}}\) = -36 < 0
∴ The profit f(x) is maximum for x = 2
The maximum profit will be P(2) =
= -41 + 72(2) – 18(4)
= 31
Question 10.
The profit function P(x) of a company selling x items is given by P(x) = -x³ + 9x² – 15x – 13 where x represents thousands of units. Find the absolute maximum profits if the company can manufacture a maximum of 6000 units.
Solution:
P(x) = -x³ + 9x² – 15x – 13
\(\frac{dp(x)}{dx}\) = -3x² + 18x – 15
for maximum or minimum \(\frac{dp}{dx}\) = 0
-3x² + 18x – 15 = 0
x² – 6x + 5 = 0
x² – 5x – x + 5 = 0
x(x- 5) – 1(x- 5) = 0
(x – 1) (x – 5) = 0
x = 1, 5
P(1) = -1 + 9 – 15 – 13 = -10
P(5) = -125 + 225 – 75 – 13 = 12
∴ Maximum profit = 12.
III.
Question 1.
The profit function P(x) of a company selling x items per day is given by P(x) = (150 – x) x – 1000. Find the number of items that the company should manufacture to get maximum profit. Also find the maximum profit.
Solution:
Given that tbe profit function
P(x) = (150 – x)x -1000
for maximum or minimum \(\frac{dp}{dx}\) = 0
(150 – x(1) -x (-1) = 0
150 – 2x = 0
x = 75
Now \(\frac{d^{2}p}{dx^{2}}\) = -2 < 0
∴ The profit P(x) is maximum for x = 75
The company should sell 75 tems a day the maxma profit will be P (75) = 4625.
Question 2.
Find the absolute maximum and absolute minimum of f(x) = 8x³ + 81x² – 42x – 8 on [-8, 2].
Solution:
f(x) = 8x³ + 81x² – 42x – 8
f'(x) = 24x²+ 162x – 42
For maximum or minimum, f'(x) = 0
24x² + 162x – 42 = 0
4x² + 27x – 7 = 0
4x² + 28x – x – 7 = 0
4x(x + 7) – 1(x + 7) = 0
(x + 7) (4x – 1) = 0
x = – 7 or \(\frac{1}{4}\)
f(- 8) = 8(-8)³ + 81(-8)² – 42(-8) -8
= – 8(512) + 81(64) + 336 – 8
= -4096 + 5184 + 336 – 8
= 5520 – 4104
= 1416
f(2) = 8(2)³ + 81 (2)² – 42(2) – 8
= 64 + 324 – 84 – 8
= 296
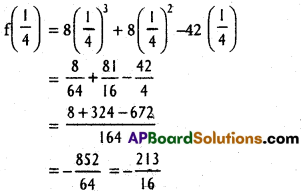
f(-7) = 1246
Absolute maximum = 1416
Absolute minimum = \(\frac{-216}{16}\)
Question 3.
Find two positive integers whose sum is 16 and the sum of whose squares is minimum.
Solution:
Suppose x and y are the sum value
x + y =16
⇒ y = 16 – x
f(x) = x² + y² = x² + (16 – x)²
= x² + 256 + x² – 32x
f'(x) = 4x – 32
for maximum or minimum f'(x) = 0
⇒ 4x – 32 = 0
4x = 32 x = 8
f”(x) = 4 > 0
∴ f(x) is minimum when x = 8
y = 16 – x = 16 – 8 = 9
∴ Required number are 8, 8.

Question 4.
Find two positive integers x and y such that x + y = 60 and xy3 is maximum.
Solution:
x + y = 60 ⇒ y = 60 – x ………… (1)
Let p = xy³ = x(60 – x)³
\(\frac{dp}{dx}\) = x³(60 – x)²(-1) + (60-x)³
= -3x (60 – x)² + (60 – x)³
= (60 – x)² [-3x + 60 – x]
= (60 – x)² (60 – 4x) = 4(60 – x)² (15 – x)
\(\frac{d^{2}p}{dx^{2}}\) = 4[(60-x)² (-1) + (15-x) 2(60-x) (-1)]
= 4(60 – x) [-60 + x – 30 + 2x]
= 4(60 – x) (3x – 90)
= 12(60 – x) (x – 30)
For maximum or minimum \(\frac{dp}{dx}\) = 0
⇒ 4(60 – x)2 (15 -x) = 0
⇒ x = 60 or x = 15 ; x cannot be 60
∴ x = 15 ⇒ y = 60 – 15 = 45.
(\(\frac{d^{2}p}{dx^{2}}\))x = 15 = 12(60 – 15) (15 – 30) < 0
⇒ p is maximum
∴ Required numbers are 15, 45.
Question 5.
From a rectangular sheet of dimensions 30 cm x 80 cm four equal squares of side x cm are removed at the comers and the sides are then turned up so as to form an open rectangular box. Find the value of x, so that the volume of the box is the greatest?
Solution:
Length of the box = 80 – 2x = l
Breadth of the box = 30 – 2x = b
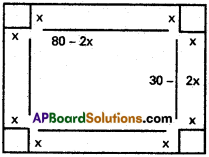
Height of the box = x = h
Volume = lbh = (80 – 2x) (30 – 2x). x
= x (2400 – 220 x + 4x²)
f(x) = 4x³ – 220 x² + 2400x
f'(x) = 12x² – 440x + 2400
= 4 [3x² – 110 x + 600]
f'(x) = 0
⇒ 3x² – 110 x +600 = 0

f(x) is maximum when x = \(\frac{20}{3}\)
Volume of the box is maximum when x = \(\frac{20}{3}\) cm
Question 6.
A window is in the shape of a rectangle surmounted by a semi-circle. If the peri-meter of the window is 20 feet, find the maximum area.
Solution:
Let length of the rectangle be 2x and breadth be y so that radius of the semi-circle is x.
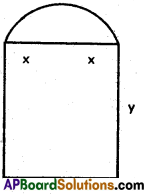
Perimeter = 2x + 2y + π. x = 20
2y = 20 – 2x – πx.
y = 10 – x – \(\frac{\pi}{2}\). x
Area = 2xy + \(\frac{\pi}{2}\). x²
= 2x(10 – x – \(\frac{\pix}{2}\)) + \(\frac{\pi}{2}\)x²
= 20x – 2x² – πx² + \(\frac{\pi}{2}\) x²
f(x) = 20x – 2x² – \(\frac{\pi}{2}\) x²
f'(x) = 0 ⇒ 20 – 4x – πx = 0
(π + 4)x = 20
x = \(\frac{20}{\pi+4}\)
f”(x) = -4 – π < 0
f(x) is a maximum when x = \(\frac{20}{\pi+4}\)

Question 7.
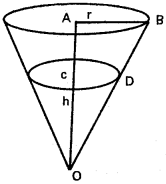
If the curved surface of right circular a cylinder inscribed in a sphere of radius r is maximum, show that the height of the cylinder is √2r.
Solution:
Suppose r is the radius and h be the height of the cylinder.
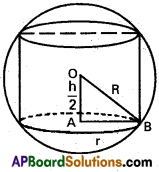
From ∆OAB, OA² + AB² = OB²
r² + \(\frac{h^{2}}{4}\) = R² ; r² = R² – \(\frac{h^{2}}{4}\)
Curved surface area = 2πrh

f(h) is greatest when h = √2 R
i.e., Height of the cylinder = √2 R.

Question 8.
A wire of length l is cut into two parts which are bent respectively in the form of a square and a circle. What are the lengths of the pieces of the wire respe-ctively so that the sum of the areas is the least?
Solution:
Suppose x is the side of the square and r is the radius of the circle.

Given 4x + 2πr = l
4x = l – 2πr
r = \(\frac{1-2 \pi r}{4}\)
Sum of the area = x² + πr²
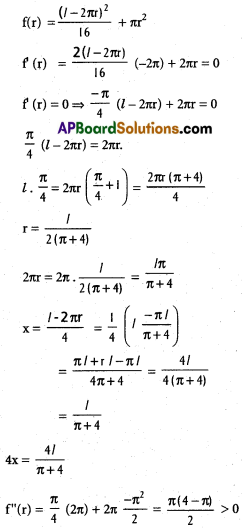
∴ f(r) is least when r = \(\frac{l}{ 2(\pi+4)}\)
Sum of the area is least when the wire is cut into pieces of length \(\frac{\pi l}{\pi+4}\) and \(\frac{4l}{\pi+4}\)
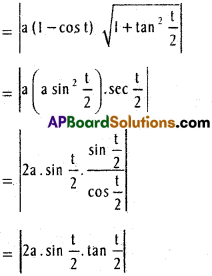
![]()
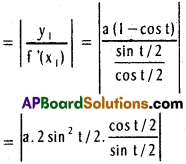
![]()
![]()


 is Vander Waals equation of state, a, b are Vander Waals parameters.
is Vander Waals equation of state, a, b are Vander Waals parameters.