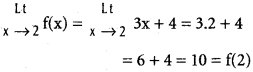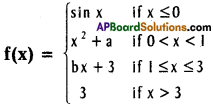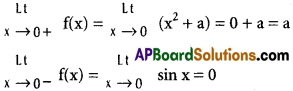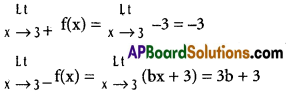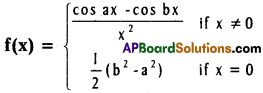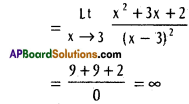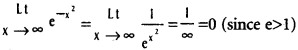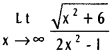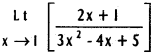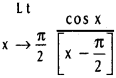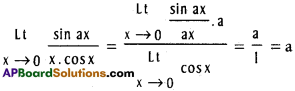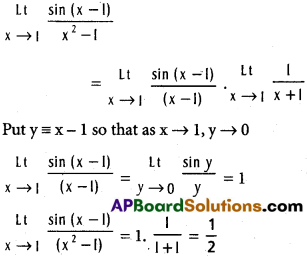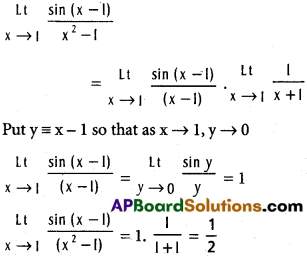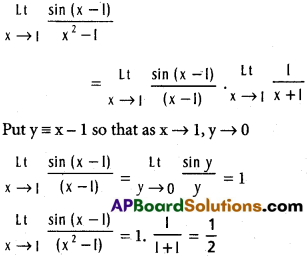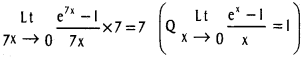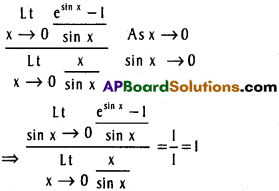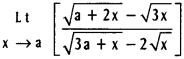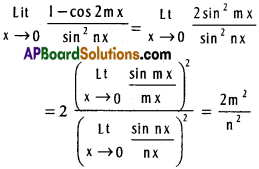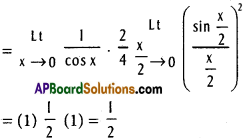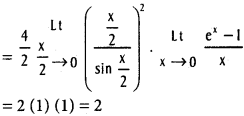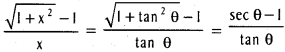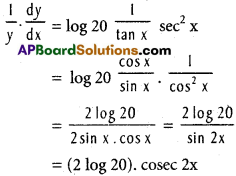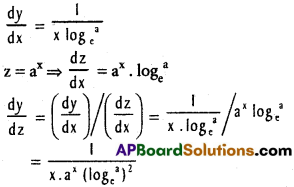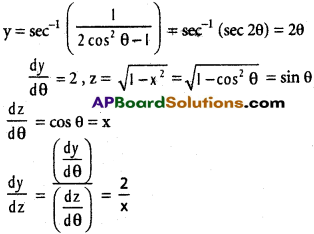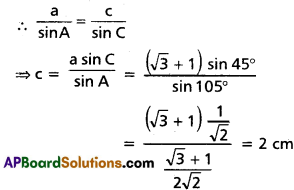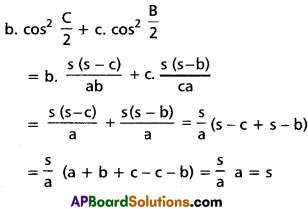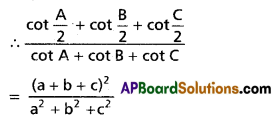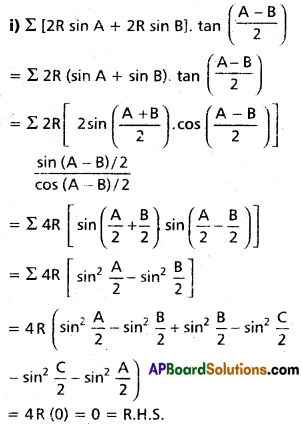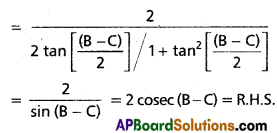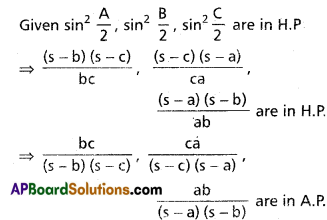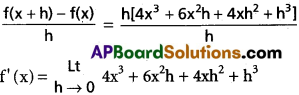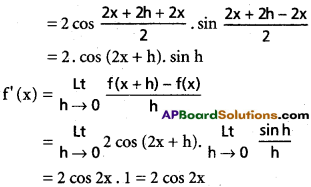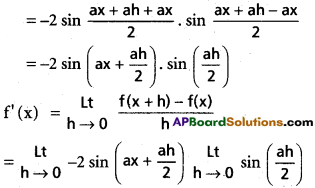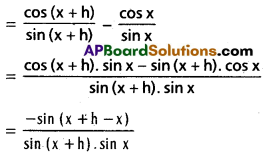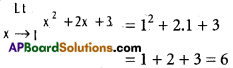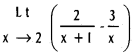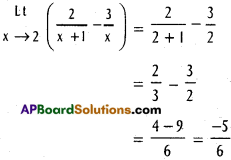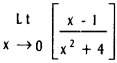Inter 1st Year

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(a)

I.

Question 1.
Find ∆y and dy for the following functions for the values of x and ∆x which are shown against each of the functions,
i) y = x² + 3x + 6, x = 10, ∆x = 0.01.
Solution:
∆y = f(x + ∆x) – f(x)
= f(10.01)-f(10)
= E(10.01)² + 3(10.01) + 6] – [10² + 3(10) + 6]
= 100.2001 +30.03 + 6 – 100 – 30 – 6
= 0.2001 + 0.03
= 0.2301
y = x² + 3x + 6
dy = (2x + 3) dx
= (2.10 + 3) (0.01) = 0.23

ii) y = e^x + x, x = 5 and ∆x = 0.02
Solution:
∆y = f(x + ∆x) – f(x)
= f(5 + 0.02) – f(5)
= f(5.02) – f(5)
= (e^5.02 + 5.02) – (e⁵ + 5)
= e^5.02 – e⁵ + 0.02
= e⁵ (e^0.02 – 1) + 0.02
dy = f'(x) ∆x = (e^x + 1) ∆x
= (e⁵ + 1) (0.02)

iii) y = 5x² + 6x + 6, x = 2 and ∆x = 0.001
Solution:
∆y’= f(x + ∆x) – f(x)
= f(2 +0.001) – f(2)
= f(2.001) – f(2)
= (5(2.001)² + 6(2.001) + 6) – (5(2)² + 6(2) +6)
= 20.0200 + 12.0060 + 6 – 20 – 12 – 6
= 0.026005
dy = f'(x) ∆x = (10x + 6) ∆x
= (26) (0.001) = 0.0260.

iv) y = 2 \(\frac{1}{x+2}\) x = 8 and ∆x = 0.02
Solution:
f(x) = \(\frac{1}{x+2}=\frac{1}{10}\) = 0.1000
f(x + ∆x) = \(\frac{1}{x+\Delta x+2}=\frac{1}{10+0.02}=\frac{1}{10.02}\) = 0.0998
∆y = f(x + ∆x) – f(x)
= \(\frac{1}{x+\Delta x+2}-\frac{1}{1+x}=\frac{1}{10.02}=\frac{1}{10}\)
= 0.0998 003992 – 0.1000 = – 0.0001996
dy = f'(x) ∆x = \(\frac{-1}{1+x^{2}}\) ∆x
= \(\frac{-1}{100}\)(0.02) = -0.0002

v) y = cos (x), x = 60° and ∆x = 1°
Solution:
∆y = f(x + ∆x) – f(x)
= cos (x + ∆x) – cos x
= cos (60° + 1°) – cos 60°
= cos 61° – cos 60°
= 0.4848 – \(\frac{1}{2}\) = 0.4848 – 0.5 = – 0.0152
dy = f'(x) ∆x
= — sin x ∆x
= – sin 60°(1°) = \(\frac{-\sqrt{3}}{2}\) (0.0174)
= – (0.8660) (0.0174) = – 0.0151.

II.

Question 1.
Find the approximations of the following.
i) √82
Solution:
82 = 81 + 1 = 81(1 + \(\frac{1}{81}\))
∴ x = 81, ∆x = 1, f(x) = 77
dy = f'(x). ∆x = \(\frac{1}{2\sqrt{x}}\). ∆x = \(\frac{1}{2\sqrt{81}}\).1
= \(\frac{1}{18}\) = 0.0555
f(x + δx) – f(x) ≅ dy
f(x + δx) ≅ f(x) + dy
= √81 + 0.0555
= 9 + 0.0555
i.e., √82 = 9.0555 = 9.056

ii) \(\sqrt[3]{65}\)
Solution:
Let x = 64, ∆x = 1, f(x) = \(\sqrt[3]{x}\)
f'(x) = \(\frac{1}{3}\)x^-2/3
f(x + ∆x) ≅ f(x) + f'(x)∆x
\(\sqrt[3]{65}\) ≅ \(\sqrt[3]{x}\) + \(\frac{1}{3}\)x^-2/3 ∆x
≅ \(\sqrt[3]{65}+\frac{1}{3}\)(4)^-2/3(I)
≅ 4 + \(\frac{1}{3}\)(\(\frac{1}{16}\))
≅ 4 + \(\frac{1}{48}\)
≅ \(\frac{192+1}{48}\)
≅ \(\frac{193}{48}\) ≅ 4.0208

iii) \(\sqrt{25.001}\)
Solution:
Letx = 25, ∆x- 0.001
f(x) = √x
dy = f'(x) ∆x
= \(\frac{1}{2\sqrt{x}}\) ∆x = \(\frac{1}{2\sqrt{25}}\) (0.001) = \(\frac{0.001}{10}\) = 0.0001
f(x + ∆x) ≅ f(x) + dy
≅ √25 + 0.0001
≅ 5.0001

iv) \(\sqrt[3]{7.8}\)
Solution:
Let x = 8, ∆x = -0.2, f(x) = \(\sqrt[3]{x}\)
dy = f'(x). ∆x
= \(\frac{1}{3}\)x^-2/3. ∆x = \(\frac{1}{3x^{2/3}}\) . ∆x
dy = \(\frac{1}{3(8)^{2/3}}\)(-0.2)
= – \(\frac{1}{3}\)
\(=-\frac{0.2}{3 \times 4}=-\frac{0.2}{12}\)
f(x + δx) – (x) ≅ dy
f(x + δx) ≅ f(x) + dy
= \(\sqrt[3]{8}\) – 0.0166
= 2 – 0.0166
= 1.9834
∴ \(\sqrt[3]{7.8}\) = 1.9834

v) sin (62°)
Solution:
Let x = 60°, ∆x = 2°, f(x) = sin x
dy = f'(x) ∆x
= cosx ∆x
= cos 60° ∆x
= \(\frac{1}{2}\) (2°)
= \(\frac{1}{2}\) 2(0.0174) = 0.0174

f(x + ∆x) ≅ f(x) + dy
≅ sin 60° + 0.0174
≅ \(\frac{\sqrt{3}}{2}\) + 0.0174
≅ 0.8660 + 0.0174
≅ 0.8834

vi) cos (60° 5′)
Solution:
Let x = 60°, Ax = 5′ = \(\frac{5}{60}\)×\(\frac{\pi}{180}=\frac{\pi}{2160}\)
= 0.001453
f(x) = cos x
dy = f'(x) ∆x = – sin x ∆x
= – sin 60° (0.001453)
= \(\frac{-\sqrt{3}}{2}\) (0.001453)
= – 0.8660 (0.001453)
= -0.001258

f(x + ∆x) ≅ f(x) + dy
≅ cos x + dy
≅ cos 60° + 0.001258
≅ 0.5 – 0.001258
≅ 0.4987.

vii) \(\sqrt[4]{17}\)
Solution:
Let x – 16, ∆x = 1, f(x) = \(\sqrt[4]{x}\) = x^¼
dy = f'(x) ∆x
= \(\frac{1}{4}\) x^¼-1 ∆x
= \(\frac{1}{4}\) x^-3/4 ∆x
= \(\frac{1}{4}\) (16)^-3/4 (I)
= \(\frac{1}{32}\) = 0.0312

f(x + ∆x) ≅ f(x) + dy
≅ \(\sqrt[4]{x}\) + 0.0312
≅ 2 + 0.0312
≅ 2.0312

Question 2.
If the increase in the side of a square is 4% then find the approximate percentage of increase in the area of the square.
Solution:
Let x be the side and A be the area of square
A = x²

Question 3.
The radius of a sphere is measured as 14 cm. Later it was found that there is an error 0.02 cm in measuring the radius. Find the approximate error in surface of the sphere.
Solution:
Let s be the surface of the sphere
r’ = 14, ∆r = 0.02
s = 4πr²
∆s = 4π 2r ∆r
∆s = 8π (14) (0.02)
= 2.24π
= 2.24 (3.14)
= 7.0336.

Question 4.
The diameter of a sphere is measured to be 40 cm. If an error of 0.02 cm is made in it, then find approximate errors in volume and surface area of the sphere.
Solution:
Let v be the value of sphere
v = \(\frac{4}{3}\) πr³ = \(\frac{4 \pi}{3}\)[latex]\frac{d}{2}[/latex]³
= \(\frac{4 \pi}{3} \frac{d^{3}}{8}=\frac{\pi d^{3}}{6}\)
∆v = \(\frac{\pi}{6}\)3d² ∆d
= \(\frac{\pi}{2}\) (40)² (0.02)
= π(1600) (0.01)
= 16π.

Surface Area s = 4πr²
s = 4π [latex]\frac{d}{2}[/latex]²
s = 4π\(\frac{d^{2}}{4}\)
s = πd²
∆s = π2d ∆d
= π2d (40) (0.02)
= 1.6π.

Question 5.
The time t, of a complete oscillation of a simple pendulum of length l is given by t = \(2 \pi \sqrt{\frac{1}{g}}\) where g is gravitational constant. Find the approximate percen-tage of error in t when the percentage of error l is 1%.
Sol. Given t = \(2 \pi \sqrt{\frac{1}{g}}\)
log t = log 2π + \(\frac{1}{2}\) {(log l – log)}

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(e) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(e)

I.

Question 1.
Is the function f, defined by \(f(x)=\left\{\begin{array}{l}
x^{2} \text { if } x \leq 1 \\
x \text { if } x>1
\end{array}\right.\) continuous on R?
Solution:

f is continuous at x = 1
f is continuous on R.

Question 2.
Is f defined by f(x) = \(=\left\{\begin{array}{cc}
\frac{\sin 2 x}{x}, & \text { if } x \neq 0 \\
1 & \text { if } x=0
\end{array}\right.\) continuous at 0?
Solution:

f is not continuous at 0

Question 3.
Show that the function f(x) = [cos (x¹⁰ + 1)]^1/3, x ∈ R is a continuous function.
Solution:
We know that cos x is continuous for every x ∈ R
∴ The given function f(x) is continuous for every x ∈ R.

II.

Question 1.
Check the continuity of the following function at 2.

Solution:

f(x) is not continuous at 2.

Question 2.
Check the continuity of f given by f(x) = \(\begin{cases}\frac{\left[x^{2}-9\right]}{\left[x^{2}-2 x-3\right]} & \text { if } 0<x<5 \text { and } x \neq 3 \\ 1.5 & \text { if } x=3\end{cases}\) at the point 3.
Solution:

f(x) is continuous at x = 3.

Question 3.
Show that f, given by f(x) = \(\frac{x-|x|}{x}\) (x ≠ 0) is continuous on R – {0}.
Solution:
Case (i) : a > 0 ⇒ |a| = a

If x = 0, f(a) is not defined
f(x) is not continuous at ’0′
∴ f(x) is continuous on R – {0}

Question 4.
If f is a function defined by

then discuss the continuity of f.
Solution:
Case (i) : x = 1

f(x) is not continuous at x > 1

Case (ii) : x = -2

f(x) is not continuous at x = -2.

Question 5.
If f is given by f(x) = \(=\left\{\begin{array}{cl}
k^{2} x-k & \text { if } x \geq 1 \\
2 & \text { if } x<1
\end{array}\right.\) is a continuous function on R, then find the values of k.
Solution:

2 = k² – k
k² – k – 2 = 0
(k – 2) (k + 1) = 0
k = 2 or – 1

Question 6.
Prove that the functions ‘sin x’ and ‘cos x’ are continuous on R.
Solution:
i) Let a ∈ R

∴ f is continuous at a.

ii) Let a ∈ R

∴ f is continuous at a.

III.

Question 1.
Check the continuity of ‘f given by

at the points 0, 1 and 2.
Solution:
i)
∴ f(x) is continuous at x = 0

ii)
∴ f(x) is continuous at x = 1

iii)
∴ f(x) is continuous at x = 2

Question 2.
Find real constant a, b so that the function f given by

is continuous on R.
Solution:

Since f(x) is continuous on R
LHS = RHS ⇒ a = 0

Since f(x) is continuous on R.
LHS = RHS
3b + 3 = -3
3b = – 6 ⇒ b = -2

Question 3.
Show that

where a and b are real constants, is continuous at 0.
Solution:

∴ f(x) is continuous at x = 0

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(d) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(d)

I. Compute the following limits.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

II.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

III.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(c)

I. Computer the following limits.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:
As x → 0
⇒ 7x → 0

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

II.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:
By L. Hospital rule

III.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(b)

Find the right and left hand limits of the functions in 1,2,3 of I and 1,2, of II at the point a mentioned against them. Hence, check whether the functions have limits at those a’s.

I.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

II.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:
x → 2 – ⇒ x < 2
x – 2 < 0
|x – 2| = – (x – 2)

Question 4.

Solution:
x → 0 + ⇒ x > 0
|x| = x

Question 5.

Solution:

Question 6.

Solution:

III.

Question 1.

Solution:

∴ LHL ≠ RHL
Limit does not exists.

Question 2.

Solution:

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(d) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(d)

I.

Question 1.
If y = \(\frac{2x+3}{4x+5}\) then find y”
Solution:
y = \(\frac{2x+3}{4x+5}\)
Differentiating w.r.to x

Question 2.
y = ae^nx + be^-nx nx then prove that y” = n²y
Solution:
y = ae^nx + be^-nx
y₁ = na e^nx – nb e^-nx
y_{2 = n² . ae^nx + n² be^-nx
y”= n² (ae^nx + b.e^-nx)
= n²y}

II.

Question 1.
Find the second order derivatives of the following functions f(x)
i) cos³ x
Solution:
y = cos³ x = \(\frac{1}{4}\) [cos 3x + 3 cos x]
y’ = \(\frac{1}{4}\) [- 3 sin 3x – 3 sin x]
y” = \(\frac{1}{4}\) (- 9 cos 3x – 3 cos x)
= – \(\frac{1}{4}\) (3 cos x + 9 cos 3x)
= – \(\frac{3}{4}\) (cos x + 3 cos 3x)

ii) y = sin⁴ x
Solution:
y = sin⁴ x = (sin²x)² = (\(\frac{(1-\cos 2 x)^{2}}{2}\))
= \(\frac{1}{4}\) [1 – 2 cos 2x + cos² 2x]
= \(\frac{1}{4}\) [1 – 2cos 2x + \(\frac{1+\cos 4 x}{2}\)]
= \(\frac{1}{8}\) [2 – 4 cos 2x + 1 + cos 4x]
= \(\frac{1}{8}\)(3 – 4 cos 2x + cos 4x)
y’ = \(\frac{1}{8}\) (8 sin 2x – 4 sin 4x)
y” = \(\frac{1}{8}\) (16 cos 2x-16 cos 4x)
= 2 (cos 2x – cos 4x)

iii) log (4x² – 9)
Solution:
y = log (4x² – 9)
= log (2x – 3) (2x + 3)
= log (2x – 3) + log (2x + 3)

iv) y = e^-2x sin³ x
Solution:
y = e^-2x. sin³ x
y’ = e^-2x (3 sin² x. cos x) + sin3 x (e^-2x) (-2)
= e^-2x [3 sin² x. cos x – 2 sin³ x)
\(\frac{d^{2} y}{d x^{2}}\) = e^-2x [3 sin² x (- sin x) + 3 cos x (2 sin x) cos x – 6 sin² x cos x) – 2. e^-2x
[3 sin² x. cos x – 2 sin³ x]
= e^-2x [6 sin x. cos² x – 6 sin² x. cos x – 3 sin³ x. – 6 sin² x. cos x + 4 sin³ x)
= e^-2x [sin³ x – 12 sin² x. cos x + 6 sin x. cos² x)

v) e^x sin x cos 2x
Solution:
y = e^x. sin x. cos 2x = \(\frac{e^{x}}{2}\) (2 cos 2x. sin x)
= \(\frac{e^{x}}{2}\) (sin 3x – sin x)
y’ = \(\frac{1}{2}\) [e^x(3 cos 3x – cos x) + e^x (sin 3x – sin x)
y”= \(\frac{1}{2}\) [ex (- 9 sin 3x + sin x) + e^x (3 cos 3x – cos x) + e^x (3 cos 3x – cos x) + e^x (sin 3x – sin x)]
= \(\frac{e^{x}}{2}\) [- 9 sin 3x + sin x + 3 cos 3x – cos x + 3 cos 3x cos x + sin 3x – sin x]
= \(\frac{e^{x}}{2}\) [6 cos 3x – 8 sin 3x – 2 cos x]
= e^x [3 cos 3x – 4 sin 3x – cos x]

vi) Tan^-1\(\frac{1+x}{1-x}\)
Solution:
y = tan^-1\(\frac{1+x}{1-x}\)
Put x = tan θ

∴ f(x) = \(\frac{\pi}{4}\) + tan^-1 (x)
Diff. w.r.to x
f'(x) = 0 + \(\frac{1}{1+x^{2}}\)
f”(x) = (-1) (1 + x²)^-2 (2x)
f”(x) = \(\frac{-2 x}{\left(1+x^{2}\right)^{2}}\)

vii) tan^-1\(\frac{3x-x^{3}}{1-3x^{2}}\)
Solution:
f(x) = tan^-1\(\frac{3x-x^{3}}{1-3x^{2}}\) ; Put x = tan θ
f(x) = tan^-1\(\left(\frac{3 \tan \theta-\tan ^{3} \theta}{1-3 \tan ^{2} \theta}\right)\)
= tan^-1(tan 3θ) = 3θ
∴ f(x) = tan^-1 (x)
f'(x) = 3\(\frac{1}{1+x^{2}}\) = \(\frac{3}{1+x^{2}}\)
Again Diff. w.r.to x
f”(x) = (3) (-1) (1 + x²)^-2 (2x)
⇒ f”(x) = \(\frac{-6 x}{\left(1+x^{2}\right)^{2}}\)

II. Prove the following.
If y = ax^{n + 1} + bx^-n
then x²y” = n(n + 1) y.
Solution:
y = ax^{n + 1} + bx^-n
y_{1 = (n + 1). axⁿ – n bx^-n-1
y2 = n(n + 1). ax^n-1 + n(n + 1) bx^-n-2
∴ x²y2 = n(n + 1) axⁿ⁺¹ + n(n + 1) bx^-n
= n(n + 1) (axn+1+bx_n) = n(n + 1) y
∴ x²y” = n(n + 1) y}

ii) If y = a cos x + (b + 2x) sin x, then y” + y = 4 cos x
Solution:
\(\frac{dy}{dx}\) = y’ = a(-sin x) + (b + 2x) \(\frac{d}{dx}\) (sin x) + sin x \(\frac{d}{dx}\) (b + 2x)
= – a sin x + (b + 2x) cos x + sin x.2
\(\frac{d^{2} y}{d x^{2}}\) = y” = – a cos x + (b + 2x) (- sin x) + cos x (2) + 2 cos x
L.H.S. = y” + y = – a cos x + (b + 2x) (- sin x) + 2 cos x + 2 cos x + a cos x+ (b + 2x) sinx = 4 cosx

iii) If y = 6 (x + 1) + (a + bx) e^3x then y” – 6y’ + 9y = 54 x + 18
Solution:
y’ = 6 \(\frac{d}{dx}\) (x + 1) + (a + bx) \(\frac{d}{dx}\) (e^3x) + e^3x \(\frac{d}{dx}\) (a + bx)
= 6(1) + (a + bx) 3e^3x + e^3x. b.
y” = 0 + 3 (a + bx) \(\frac{d}{dx}\) e^3x + 3e^3x \(\frac{d}{dx}\) (a + bx) + b \(\frac{d}{dx}\) (e^3x)
= 3(a + bx) 3e^3x + 3e^3x(b) + b. 3e^3x
= 9(a + bx) e^3x + 6b e^3x
Now L.H.S. = y” – 6y’ + 9y = 9(a + bx) e^3x + 6be^3x – 6[6 + 3(a + bx)e^3x + be^3x] + 9 [6(x + 1) + (a + bx)e^3x]
= 9(a + bx) e^3x + 6b e^3x – 36 – 18(a + bx)e^3x – 6be^3x + 54x + 54 + 9(a + bx) e^3x = 54x + 18

iv) If ay⁴ = (x + b)⁵ then 5y y” = (y’)²
Solution:
ay⁴ = (x + b)⁵ ; y⁴ = \(\frac{\left(x+b\right)^{2}}{a}\)

v) If y = a cos (sin x) + b sin (sin x) then y” + (tan x) y’ + y cos² x = 0
Solution:
y = a cos (sin x) + b sin (sin x) …………. (1)
Differentiating w.r.to x
y₁ = – a sin (sin x) cos x + b cos (sin x). cos x = [- a sin (sin x) + b cos (sin x)j cos x ………. (2)
Differentiating again w.r.to x.
y₂ = – sin x [-a sin (sin x) + b cos (sin x)] + cos x [- a cos (sin x) cos x – b sin (sin x) cos x]
= – sin x. \(\frac{y_{1}}{\cos x}\) = -cos² x.y
From (1) and (2),
⇒ y₂ + (tan x) y₁ + y cos² x = 0

III.

i) If y = 128 sin³ x cos⁴ x, then find y”.
Solution:
f(x) = 128 sin³ x. cos⁴ x
D.w.r. to x
f'(x)= 128 [sin³ x {4cos³ x (-sinx)} + cos⁴ x {3sin² x. cos x}]
= 128 [3sin² x cos⁵ x – 4sin⁴ x cos³ x]
Again D.w.r to x.
f”(x)= 128 {3 [sin² x 5cos⁴ x . (-sinx) + cos⁵ x. 2sinx cosx] – 4 [sin⁴ x. 3. cos2x (-sinx) + cos³ x. 4 sin³ x. cos x]}
= 128 [-15sin³ x . cos⁴ x + 6sin x cos⁶ x + 12 sin⁵ x cos² x- 16sin³ x cos⁴ x]
f”(x)= 128 [6sinx cos6x + 12sin⁵ x. cos² x – 31sin³ x. cos⁴ x]

ii) If y = sin 2x sin 3x sin 4x, then find y”.
Solution:
f(x) = sin 2x sin 3x sin 4x
= \(\frac{1}{2}\)sin 2x [2sin 4x. sin 3x]
= \(\frac{1}{2}\)sin 2x [cos x – cos 7x]
= \(\frac{1}{2}\) [sin 2x . cos x – cos 7x. sin 2x]
= \(\frac{1}{2}\)×\(\frac{1}{2}\) [2 sin2x. cosx – 2 cos7x. sin2x]
= \(\frac{1}{4}\) [(sin3x + sinx) – (sin9x – sin5x)]
= \(\frac{1}{4}\) [-sin9x + sin5x + sin3x + sinx]
D.w.r. to x
f'(x) = \(\frac{1}{4}\) [-9 cos 9x + 5 cos 5x + 3 cos 3x + cos x]
D.w.r. to x
f”(x) = \(\frac{1}{4}\) [81 sin 9x – 25sin 5x – 9sin 3x – sin x]

iii) If ax² + 2hxy + by² = 1 then prove that
\(\frac{d^{2} y}{d x^{2}}=\frac{h^{2}-a b}{(h x+b y)^{3}}\)
Solution:
Given ax² + 2hxy + by² = 1
Differentiating w.r. to x
a.2x + 2h(x. \(\frac{dy}{dx}\) + y) + b . 2y\(\frac{dy}{dx}\) = 0
2ax + 2hx. \(\frac{dy}{dx}\) + 2hy + 2by. \(\frac{dy}{dx}\) = 0
2(hx + by).\(\frac{dy}{dx}\) = -2(ax + hy)
\(\frac{dy}{dx}\) = \(\frac{-2(ax +hy)}{2(hx+by)}\) = \(\frac{(ax+hy)}{(hx+by)}\) ……… (1)
Differentiating again w.r. to x, \(\frac{d^{2} y}{d x^{2}}\)

iv) If y = ae^-bx cos(cx + d) then prove that y” + 2by’ + (b² + c²) y = 0.
Solution:
Given y = ae^-bx cos(cx + d) ……….. (1)
y₁ = a[e^-bx {- sin (cx + d)}. c. + cos (cx + d) e^-bx (-b)}
= – a. e^-bx [c sin (cx + d) + b cos (cx + d)]
= – ac.e^-bx sin (cx + d) – by
y₁ + by = – ac. e^-bx sin (cx + d) ………. (2)
Differentiating once w.r.to x
y₂ + by₁ = – ac(- b) e^-bx sin (cx + d) – ac e^-bx cos (cx + d) (+ c)
= abce^-bx sin (cx + d) -ac² e^-bx cos (cx + d)
= – b (y₁ + by) c²y [From (1) and (2)]
⇒ y₂ + by₁ + by₁ + b²y + c²y = 0.
⇒ y₂ + 2by₁ + (b² + c²) y = 0 (or)
y” + 2 by’ + (b² + c²) y = 0

v) If y = \(e^{\frac{-k}{2} x}\) (a cos nx + b sin nx) prove that then y” + ky’+ (n² + \(\frac{k^{2}}{4}\))y = 0
Solution:
Given y = \(e^{\frac{-k}{2} x}\) (a cos nx + b sin nx) ………… (1)
∴ y₁ = \(e^{\frac{-k}{2} x}\) (-n. a sin nx + n. b cos nx) + (a cos nx + b sin nx).\(e^{\frac{-k}{2} x}\) (-\(\frac{k}{2}\))
= –\(\frac{k}{2}\) . y – n.e^-kx/2 (a sin nx + b cos nx)
∴ y₁ + \(\frac{k}{2}\) y = – n.e^-kx/2 (a sin nx + b cos nx) …………. (2)
Differentiating w.r. to x k
y₂ + \(\frac{k}{2}\) y₁ = -n[{e^-kx/2 (- na cos nx – nb sin nx)}] + {(a sin nx +b cos nx).e^-kx/2 \(\frac{k}{2}\)}
= – n² e^-kx/2(a cos nx + b sin nx) – \(\frac{k}{2}\){-n.e^-kx/2 (a sin nx + b cos nx)}

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(c)

I.

Question 1.
Find the derivatives of the following functions.
i) sin^-1 (3x – 4x³)
Solution:
Put x = sin θ
y = sin^-1 (3 sin θ – 4 sin³ θ)
= sin^-1 (sin 3 θ) = 3 θ = 3 sin^-1 x.
\(\frac{dy}{dx}\) = \(\frac{3}{\sqrt{1-x^{2}}}\)

ii) cos^-1 (4X3 – 3x)
Solution:
Put x = cos θ
y = cos^-1 (4 cos³ θ – 3 cos θ)
= cos^-1 (cos 3θ) = 3θ = 3 cos^-1 x
\(\frac{dy}{dx}\) = \(\frac{3}{\sqrt{1-x^{2}}}\)

iii) sin^-1 \(\frac{3}{{1-x^{2}}}\)
Solution:
Put x tan θ ⇒ y

iv) tan^-1 \(\frac{a-x}{1+ax}\)
Solution:
Put a tan α, x = tan θ
y = tan^-1 \(\left(\frac{\tan \alpha-\tan \theta}{1+\tan \alpha \tan \theta}\right)\)
= tan^-1 (tan (α – θ)) = α – θ
= tan^-1 a – tan^-1 x;
\(\frac{dy}{dx}\) = 0 – \(\frac{1}{1+x^{2}}\) = – \(\frac{1}{1+x^{2}}\)

v) tan^-1 \(\sqrt{\frac{1-\cos x}{1+\cos x}}\)
Solution:

Differentiating w.r.to x; \(\frac{dy}{dx}\) = \(\frac{1}{2}\)

vi) sin [cos (x²)]
Solution:
\(\frac{dy}{dx}\) = cos [cos (x²)]\(\frac{d}{dx}\) [cos (x²)]
= cos [cos (x²)]. [-sin (x²)] \(\frac{d}{dx}\) (x²)
= cos [cos (x²)] [- sin (x²)]. 2x
= -2x . sin (x²).cos [cos (x²)]

vii) sec^-1 (\(\frac{1}{2x^{2}-1}\)) (0 < x < \(\frac{1}{\sqrt{2}}\))
Solution:
x = cos θ
2x² – 1 = 2 cos² θ – 1 = cos 2θ

viii) sin^-1 [tan^-1 (e^-x)]
Solution:
\(\frac{dy}{dx}\) = cos [tan^-1 (e^-x)]. [tan^-1 (e^-x)]¹
= cos (tan^-1 (e^-x)]x – \(\frac{1}{1+\left(e^{-x}\right)^{2}}\) (e^-x)¹
= \(\frac{-e^{-x}}{1+e^{-2 x}}\) . cos [tan^-1 (e^-x)]

Question 2.
Differentiate f(x) with respect to g(x) for the following.
i) f(x) = e^x, g(x) = √x
Solution:
Let y = e^x and z = √x

ii) f(x) = e^{sin x}, g(x) = sin x.
Solution:
Let y = e^{sin x} and z = sin x.

iii) f(x) = tan^-1 \(\frac{2x}{1-x^{2}}\), g(x) sin^-1 = \(\frac{2x}{1+x^{2}}\)
Solution:
Lety = tan^-1 \(\frac{2x}{1-x^{2}}\), and z = sin^-1 = \(\frac{2x}{1+x^{2}}\)
Put x = tan θ

Question 3.
If y = e^a sin^-1x the prove that \(\frac{dy}{dx}\) = \(\frac{a y}{\sqrt{1-x^{2}}}\)
Solution:
y = e^{a sin-1x}
\(\frac{dy}{dx}\) = e^{a sin-1x} (a sin^-1 x)¹
= e^{a sin-1x} . a \(\frac{1}{\sqrt{1-x^{2}}}\) = \(\frac{a y}{\sqrt{1-x^{2}}}\)

II.

Question 1.
Find the derivatives of the following function.
i) tan^-1 \(\left(\frac{3 a^{2} x-x^{3}}{a\left(a^{2}-3 x^{2}\right)}\right)\)
Solution:
Put x = a tan θ

ii) tan^-1 (sec x + tan x)
Solution:

iii) tan^-1 \(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\)
Solution:
Put x = tan θ

iv) (logx)^{tan x}
Solution:
log y = log (log x)^{tan x}
= (tan x). log (log x)
Differentiating w.r.to x
\(\frac{1}{y}\) . \(\frac{dy}{dx}\) = tan x . \(\frac{d}{dx}\) (log(log x)) + log(logx) \(\frac{d}{dx}\) (tan x)
= tan x. \(\frac{1}{log x}\) . \(\frac{1}{x}\) + log(log x). sec² x

v) (x^x)^x = x^x²
Solution:
log y = log x^x² = x². log x
\(\frac{1}{y}\) . \(\frac{dy}{dx}\) = x² . \(\frac{d(\log x)}{d x}\) + (log x ) \(\frac{d}{dx}\) (x²)
= x². \(\frac{1}{x}\) + 2x. log x
= x + 2x log x = x (1 + 2 log x).
= x (log e + log x²)
= x. log (ex²)
\(\frac{dy}{dx}\) = y. x. log (ex²)
= x^x² . x. log (ex²)
= x^{x² +1} log (ex²)

vi) 20^{log (tan x)}
Solution:
log y = log (20)^{log (tan x)}
= log (tan x) log 20
Differentiating w. r. to x

\(\frac{dy}{dx}\) = y. (2 log 20). cosec 2x
= 20^{log (tan x)} (2 log 20). cosec 2x

vii) x^x + e^ex
Solution:
Let y₁ = x^x and y₂ = e^ex so that y = y₁ + y₂.
y₁ = x^x ⇒ log y₁ = log x^x = x log x

viii) x. log x. log (log x)
Solution:
\(\frac{dy}{dx}\) = x. log x \(\frac{d}{dx}\) (log. (log x)) + log (log x) logx. 1 + x. log (log x) \(\frac{1}{x}\).
= x log x. \(\frac{1}{log x}\) . \(\frac{1}{x}\) + log x. log (log x) + log (log x)
= 1 + log (logx) (1 + logx) = 1 + log (logx) + log x log (log x)
= log e + log (log x) + log x. log (log x)
= log (e log x) + log x. log (log x)

ix) e^-ax² sin (x log x)
Solution:
\(\frac{dy}{dx}\) = e^-ax² . \(\frac{d}{dx}\) (sin (x log x)) dx + sin (x log x) \(\frac{d}{dx}\) (e^-ax²)
= e^-ax² cos (x log x). (x . \(\frac{1}{x}\) + log x) + sin (x log x) e^-ax² (-2ax)
= e^-ax² [(cos (x log x) (1 + log x) – 2 ax. sin (x log x)]
= e^-ax² (cos (x log x) (log ex) -2 ax. sin (x log x))

x) sin^-1\(\left(\frac{2^{x+1}}{1+4^{x}}\right)\) (Put 2ⁿ = tan θ)
Solution:
sin^-1\(\left(\frac{2^{x+1}}{1+4^{x}}\right)\)
Put 2^x = tan θ.

Question 2.
Find \(\frac{dy}{dx}\) for the following functions.
i) x = 3 cos t – 2 cos³ t,
y = 3 sin t – 2 sin³ t
Solution:
\(\frac{dx}{dt}\) = – 3 sin t – 2(3 cos² t) (- sin t)
= – 3 sin t + 6 cos² t (sin t)
= 3 sin t (2 cos² t – 1)
= 3 sin t. cos 2t
y = 3 sin t – 2 sin³ t
\(\frac{dy}{dt}\) = 3 cos t – 2 (3 sin² t) (- cos t)
= 3 cos t (1 – 2 sin² t)
= 3 cos t. cos 2t
\(\frac{dy}{dx}\) = \(\frac{\left(\frac{\mathrm{dy}}{\mathrm{dt}}\right)}{\left(\frac{\mathrm{dx}}{\mathrm{dt}}\right)}=\frac{3 \cos t \cos 2 t}{3 \sin t \cos 2 t}\) = cot t

ii) x = \(\frac{3 a t}{1+t^{3}}\), y = \(\frac{3 a t^{2}}{1+t^{3}}\)
Solution:

iii) x = a (cos t + t sin t), y = a (sin t – t cos t)
Solution:
\(\frac{dx}{dt}\) = a (- sin t + t cos t + sin t) = at cos t
∴ y = a (sin t – t cos t)
\(\frac{dy}{dt}\) = a (cos t – cos t + t sin t) = at sin t
\(\frac{dy}{dx}\) = \(\frac{\left(\frac{\mathrm{dy}}{\mathrm{dt}}\right)}{\left(\frac{\mathrm{dx}}{\mathrm{dt}}\right)}=\frac{at\cos t}{at\cos t}\) = tan t

iv) x = a\(\left[\frac{\left(1-t^{2}\right)}{1+t^{2}}\right], \mathbf{y}=\frac{2 b t}{1+t^{2}}\)
Solution:

Question 3.
Differentiate f(x) with respect to g(x) for the following.
i) f(x) = log_a^x, g(x) = a^x.
Solution:
y = log_a^x = \(\frac{\log x}{\log _{c}^{a}}\)

ii) f(x) = sec^-1 (\(\frac{1}{2x^{2}-1}\)) g(x) = \(\sqrt{1-x^{2}}\)
Solution:
Let y = sec^-1 (\(\frac{1}{2x^{2}-1}\)) and z = \(\sqrt{1-x^{2}}\)
Put x = cos θ

iii) f(x) = tan^-1\(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\), g(x) = tan^-1 x.
Solution:
Let y = tan^-1\(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) and z = tan^-1 x
x = tan z

Question 4.
Find the derivative of the function y defined implicitly by each of the following equations.
i) x⁴ + y⁴ – a² xy = 0
Solution:
Differentiate w.r.to x
4x³ + 4y³ . \(\frac{dy}{dx}\) – a²(x. \(\frac{dy}{dx}\) + y . 1 = 0)
4x³ + 4y³ . \(\frac{dy}{dx}\) – a²x\(\frac{dy}{dx}\) – a²y = 0
4y³ – a²x) \(\frac{dy}{dx}\) = a²y – 4x³ ; \(\frac{dy}{dx}\) = \(\frac{a^{2} y-4 x^{3}}{4 y^{3}-a^{2} x}\)

ii) y = x^y
Solution:
log y = log x^y = y log x
Differentiate w.r.to x

iii) y^x = x^{sin y}
Solution:
Take log on both sides
log y^x = log x^{sin y} ⇒ x. log y = (sin y) log x.
Differentiating w.r.to x

Question 5.
Establish the following.
i) If \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}\) = a(x – y), than \(\frac{d y}{d x}=\frac{\sqrt{1-y^{2}}}{\sqrt{1-x^{2}}}\)
Solution:
Given \(\sqrt{1-x^{2}}+\sqrt{1-y^{2}}\) = a(x – y)
Put x = sin θ, y = sin Φ
Differentiating w.r. to x

ii) If y = x \(\sqrt{a^{2}+x^{2}}\) + a² log (x + \(\sqrt{a^{2}+x^{2}}\)), then \(\frac{dy}{dx}\) = 2 \(\sqrt{a^{2}+x^{2}}\)
Solution:
y ⇒ x\(\sqrt{a^{2}+x^{2}}\) + a² log (x + \(\sqrt{a^{2}+x^{2}}\))

iii) If x^{log y} = log x, then
Solution:
Given x^{log y} = log x, log x^{log y} = log log x
(log y) (log x) = log(logx).
Differentiating w.r.to x

iv) If y = Tan^-1 \(\frac{2x}{1-x^{2}}\) + Tan^-1 \(\frac{3x-x^{3}}{1-3x^{2}}\) – tan^-1 \(\frac{4x-4x^{3}}{1-6x^{2}+x^{4}}\) than \(\frac{dy}{dx}\) = \(\frac{1}{1+x^{2}}\)
Solution:
Put x = tan θ

= tan^-1 (tan 2θ) + tan^-1 (tan 3θ) – tan^-1 (tan 4θ)
= 2θ + 3θ – 4θ = θ = tan^-1 x
∴ \(\frac{dy}{dx}\) = \(\frac{1}{1+x^{2}}\)

v) If x^y = y^x, then \(\frac{dy}{dx}\) = \(\frac{y(x log y – y)}{x(y log x – x)}\)
Solution:
Given x^y = y^x ; log x^y = log y^x
y log x = x log y
Differentiating w.r.to x

vi) If x^2/3 + y^2/3 = a^2/3 then \(\frac{dy}{dx}\) = -3 √y/x
Solution:
Given x^2/3 + y^2/3 = a^2/3
Differentiating w.r.to x

Question 6.
Find the derivative \(\frac{dy}{dx}\) of each of the following functions.
i) y = \(\frac{(1-2 x)^{2 / 3}(1+3 x)^{-3 / 4}}{(1-6 x)^{5 / 6}(1+7 x)^{-6 / 7}}\)
Solution:
log y = log \(\left\{\frac{(1-2 x)^{2 / 3}(1+3 x)^{-3 / 4}}{(1-6 x)^{5 / 6}(1+7 x)^{-6 / 7}}\right\}\)
= log (1 – 2x)^2/3 + log (1 + 3x)^-3/4 – log (1 – 6x)^5/6 – log (1 + 7x)^-6/7
= \(\frac{2}{3}\) log (1 – 2x) – \(\frac{3}{4}\) log (1 + 3x) – \(\frac{5}{6}\) log (1 – 6x) + \(\frac{6}{7}\) log (1 + 7x)
Differentiating w.r.to x
\(\frac{1}{y}\).\(\frac{dy}{dx}\) = \(\frac{2}{3}\) . \(\frac{1(-2)}{1-2x}\) – \(\frac{3}{4}\) . \(\frac{1}{1+3x}\) . 3

ii)

Solution:
log y = log x⁴ + log (x² + 4)^1/3 – log (4x² – 7)^1/2
= 4 log x + \(\frac{1}{3}\) log (x² + 4) – \(\frac{1}{2}\) log (4x² – 7)
Differentiating w.r.to x

iii) y = \(\frac{(a-x)^{2}(b-x)^{3}}{(c-2 x)^{3}}\)
Solution:
log y = log \(\frac{(a-x)^{2}(b-x)^{3}}{(c-2 x)^{3}}\)
= log (a – x)² + log (b – x)³ – log (c – 2x)³
= 2 log (a – x) + 3 log (b – x) – 3 log (c – 2x)
Differentiating w.r.to x

iv)

Solution:
log y = log \(\frac{x^{3}(2+3 x)^{1 / 2}}{(2+x)(1-x)}\)
= log x³ + log (2 + 3x)^1/2 – log (2 + x) – log (1 – x)
= 3 log x + \(\frac{1}{2}\) log (2 + 3x) – log (2 + x) – log (1 – x)
Differentiating w.r. to x

v) y = \(\sqrt{\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}}\)
Solution:
log y = log(\(\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}\))^1/2
= \(\frac{1}{2}\) log \(\frac{(x-3)\left(x^{2}+4\right)}{3 x^{2}+4 x+5}\)
= \(\frac{1}{2}\) (log (x – 3) + log (x² + 4) – log (3x² + 4x + 5))

III.

Question 1.
Find the derivatives of the following functions.
i) y = (sin x)^logx + x^{sin x}
Solution:
Let y₁ =(sinx)^logx, y₂ = x^{sin x} so that y = y₁ + y₂
y₁ = (sin x)^logx
log y₁= log{ (Sin x)^logx} = log x. log (sin x)
Differentiating w.r. to x

y₂ = x^{sin x}
log y₂ = (log x)^{sin x} = sin x. logx

ii) x^xx
Solution:
log y = log x(x^xx) = x^x. log X
\(\frac{1}{y}\) \(\frac{dy}{dx}\) = x^x. \(\frac{1}{x}\) + (log x). x^x (1 + log x)
[\(\frac{d}{dx}\)(x^x) = x^x (1 + log x)]
= x^x-1 [1+ x log x (log e + log x)]
= x^x-1 (1 + x. log x. log ex)
\(\frac{dy}{dx}\) = y.x^x-1 (1 + x log x. log ex)
= x^(xx) . x^x-1 (1 + x log x. log ex)
= x^xx+x-1 (1 + x log x. log ex)

iii) (sin x)^x + x^{sin x}
Solution:
Let y₁ = (sin x)^x and y₂ = x^{sin x}
so that y = y₁ + y₂
log y₁ = log (sin x)^x = x. log sin x

iv) x^x + (cot x)^x
Solution:
Let y₁ = x^x and y₂ = (cot x)^x
log y₁ = log x^x = x log x

Question 2.
Establish the following
i) If x^y + y^x = a^b then
\(\frac{dy}{dx}\) = \(-\left(\frac{y \cdot x^{y-1}+y^{x} \cdot \log y}{x^{y} \cdot \log x+x \cdot y^{x-1}}\right)\)
Solution:
Let y₁ = x^y and y₂ = y^x. so that y₁ + y₂ = a^b
logy₁ = log x^y = y logx

ii) If f(x) = sin^-1\(\sqrt{\frac{x-\beta}{\alpha-\beta}}\) and
g(x) = tan \(\sqrt{\frac{x-\beta}{\alpha-x}}\) than
f'(x) = g'(x) (β < x < α)
Solution:

iii) If a > b > 0 and 0 < x < π
f(x) = (a – b)^-1/2 . cos^-1\(\left(\frac{a \cos x+b}{a+b \cos x}\right)\), than f'(x) = (a + b cos x)^-1
Solution:
Let u = cos^-1\(\left(\frac{a \cos x+b}{a+b \cos x}\right)\)

Question 3.
Differentiate (x² – 5x + 8) (x³ + 7x + 9) by
i) Using product
ii) Obtaining a single polynomial expanding the product
iii) Logarithmic differentiation do they all give the same answer?
Solution:
Do Product rule:
y = (x² – 5x + 8) (x³ + 7x + 9)
\(\frac{dy}{dx}\) = (x² – 5x + 8) \(\frac{d}{dx}\)(x³ + 7x + 9) + (x³ + 7x + 9) \(\frac{d}{dx}\)(x² – 5x + 8)
= (x² – 5x + 8)(3x² + 7) + (x³ + 7x + 9)(2x – 5)
= 3x⁴ – 15x³ + 24x² + 7x² – 35x + 56 + 2x⁴ + 14x² + 18x – 15x³ – 35x – 45
= 5x⁴ – 20x³ + 45x² – 52x + 11 ……….. (1)

ii) Expanding the product :
Solution:
y = (x² – 5x + 8) (x³ + 7x + 9)
= 5x⁵ + 7x³ + 9x² – 5x⁴ -35x² – 45x + 8x³ + 56x + 72
= x⁵ – 5x⁴ + 15x³ – 26x² + 11x +72
\(\frac{dy}{dx}\) = 5x⁴ – 20x³ + 45x² – 52x + 11 ……….. (2)

iii) y = (x² – 5x + 8) (x³ + 7x + 9)
Solution:
log y = log (x² – 5x + 8) (x³ + 7x + 9)
= log (x² – 5x + 8) + log (x³ + 7x + 9)

= (2x – 5)(x³ + 7x + 9) + (x² – 5x + 8)(3x² + 7)
= 2x⁴ + 14x² + 18x – 5x³ – 35x – 45 + 3x⁴ -15x³ + 24x² + 7x² – 35x + 56
= 5x⁴ – 20x³ +45x² – 52x + 11 ……….. (3)
From (1), (2) and (3) we observe that all the three give same answer.

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(b)

I. Compute the following limits.

Question 1.
Find the derivatives of the following function.
i) cotⁿ x
Solution:
\(\frac{dy}{dx}\) = n. cot^n-1 x. \(\frac{d}{dx}\) (cot x)
= n. cot^n-1 x (- cosec² x)
= – n. cot^n-1 x. cosec² x

ii) cosec⁴ x
Solution:
\(\frac{dy}{dx}\) = 4.cosec³ x. \(\frac{d}{dx}\)(cosec x)
= 4. cosec³ x (- cosec x. cot x)
= – 4. cosec⁴ x. cot x

iii) tan (e^x)
=sec 2(e^x).(e^x)¹
= e^x. sec² (e^x)

iv) \(\frac{1-\cos 2 x}{1+\cos 2 x}\)
Solution:
\(\frac{2 \sin ^{2} x}{2 \cos ^{2} x}\) = tan² x \(\frac{dy}{dx}\) = 2 tan x . sec² x

v) sin^m x cosⁿ x
Solution:
\(\frac{dy}{dx}\) = (sin^m x). \(\frac{d}{dx}\) (cosⁿ x) + (cosⁿ x) \(\frac{d}{dx}\) (sin^m x)
= sin^m xn + cos^n-1 x(-sin x) + cosⁿ x. m sin^m-1 x. cos x
= m. cosⁿ⁺¹ x. sin^m-1 x – n. sin^m+1 x. cos^n-1 x.

vi) sin mx. cos nx
Solution:
\(\frac{dy}{dx}\) = sin mx \(\frac{d}{dx}\) (cos nx) + (cos nx) \(\frac{dy}{dx}\) (sin mx)
= sin mx (-n sin nx)+cos nx (m cos mx)
= m. cos mx. cos nx – n. sin mx . sin nx

vii) x tan^-1 x
Solution:
\(\frac{dy}{dx}\) = x. \(\frac{d}{dx}\) (tan^-1 x) + (tan^-1 x) \(\frac{d}{dx}\) (x)
= \(\frac{x}{1+x^{2}}\) + tan^-1 x.

viii) sin^-1 (cos x)
Solution:
= sin^-1 [sin (\(\frac{\pi}{2}\) – x)] = \(\frac{\pi}{2}\) – x
\(\frac{dy}{dx}\) = 0 – 1 = -1

ix) log (tan 5x)
Solution:

x) sinh^-1 (\(\frac{3x}{4}\))
Solution:

xi) tan^-1 (log x)
Solution:

xii) log (\(\frac{x^{2}+x+2}{x^{2}-x+2}\))
Solution:
\(\frac{dy}{dx}\) = log(x² + x + 2) – log(x² – x + 2)

xiii) log (sin^-1 (e^x))
Solution:

xiv) (sin x)² (sin^-1 x)²
Solution:

xv) y = \(\frac{\cos x}{\sin x+\cos x}\)
Solution:

xvi) \(\frac{x\left(1+x^{2}\right)}{\sqrt{1-x^{2}}}\)
Solution:

xvii) y = e^sin-1x
Solution:

xviii) y = cos (log x + e^x)
Solution:
\(\frac{dy}{dx}\) = -sin(log x + e^x) = \(\frac{d}{dx}\) (log x + e^x)
= -sin (log x + e^x) (\(\frac{1}{x}\) + e^x)

xix) y = \(\frac{\sin (x+a)}{\cos x}\)
Solution:

xx) y = cot^-1 (coses 3x)
Solution:

Question 2.
Find the derivatives of the following fountion.
i) x = sinh² y
Solution:
\(\frac{dy}{dx}\) = 2 sinh y . cosh y

ii) x = tanh² y
Solution:
\(\frac{dy}{dx}\) = 2 tanh y . sech² y

iii) x = e^{sinh y}
Solution:
\(\frac{dy}{dx}\) = e^{sinh y} \(\frac{d}{dx}\) (sinh y)
= e^{sinh y} . cosh y
= x. cosh y
\(\frac{d y}{d x}=\frac{1}{\left(\frac{d x}{d y}\right)}=\frac{1}{x \cdot \cosh y}\)

iv) x =tan (e^-y)
Solution:
\(\frac{dy}{dx}\) = sec² (e^-y) . (e^-y)¹ = -e^-y . sec² e^-y
= -e^-y(1 + tan² (e^-y) = – e^-y(1 + x²)
\(\frac{d y}{d x}=\frac{1}{\left(\frac{d x}{d y}\right)}=-\frac{1}{e^{-y}\left(1+x^{2}\right)}=-\frac{e^{y}}{1+x^{2}}\)

v) x = log (1 + sin² y)
Solution:

vi) x = log (1 + √y)
Solution:
1 + √y = e^x
√y = e^x – 1
y = (e^x – 1)²
\(\frac{dy}{dx}\) = 2(e^x – 1) . e^x = 2 √y . e^x
= 2 √y (√y + 1)
= 2(y + √y)

II. Find the derivativies of the following functions.

i) y = cos [log (cot x)]
Solution:

ii) y = sin^-1 \(\frac{1-x}{1+x}\)
Solution:

iii) log (cot (1 – x²))
Solution:

iv) y = sin [cos (x²)]
Solution:
\(\frac{dy}{dx}\) = cos [cos (x²)].\(\frac{d}{dx}\)[cos (x²)]
= cos [cos (x²)](sin (x²)).\(\frac{d}{dx}\)(x²)
= – 2x. sin (x²). cos [cos (x²)]

v) y = sin [tan^-1 (e^x)]
Solution:

vi) y = \(\frac{\sin (a x+b)}{\cos (c x+d)}\)
Solution:

vii) y = tan^-1 (tan h \(\frac{x}{2}\))
Solution:

viii) y = sinx . (Tan^-1x)²
Solution:

III. Find the derivatives of the following functions.

Question 1.
y = sin^-1 \(\left(\frac{b+a \sin x}{a+b \sin x}\right)\) (a > 0, b > 0)
Solution:
Let u = \(\frac{b+a \sin x}{a+b \sin x}\)

Question 2.
cos^-1\(\left(\frac{b+a \cos x}{a+b \cos x}\right)\) (a > 0, b > 0)
Solution:
Let u = \(\frac{b+a \cos x}{a+b \cos x}\)

Question 3.
tan^-1 \(\left[\frac{\cos x}{1+\cos x}\right]\)
Solution:
Let u = \(\frac{\cos x}{1+\cos x}\)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(b)

All problems in this exercise have reference to ΔABC.

I.

Question 1.
Express \(\Sigma r_{1} \cot \frac{A}{2}\) in terms of s.
Solution:
\(\Sigma r_{1} \cot \frac{A}{2}\) = \(\Sigma\left(s \tan \frac{A}{2}\right) \cot \frac{A}{2}\)
= Σs
= s + s + s
= 3s

Question 2.
Show that Σa cot A = 2(R + r).
Solution:
L.H.S = Σa . cot A
= Σ2R sin A \(\frac{\cos A}{\sin A}\)
= 2R Σ cos A
= \(2 R\left(1+4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2}\right)\) (From transformants)
= \(2\left(R+4 R \sin \frac{A}{2} \cdot \sin \frac{B}{2} \cdot \sin \frac{C}{2}\right)\)
= 2(R + r)
= R.H.S

Question 3.
In ∆ABC, prove that r₁ + r₂ + r₃ – r = 4R.
Solution:

Question 4.
In ∆ABC, prove that r + r₁ + r₂ – r₃ = 4R cos C.
Solution:

Question 5.
If r + r₁ + r₂ + r₃ then show that C = 90°.
Solution:

II.

Question 1.
Prove that 4(r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)²
Solution:

Question 2.
Prove that \(\left(\frac{1}{r}-\frac{1}{r_{1}}\right)\left(\frac{1}{r}-\frac{1}{r_{2}}\right)\left(\frac{1}{r}-\frac{1}{r_{3}}\right)=\frac{a b c}{\Delta^{3}}=\frac{4 R}{r^{2} s^{2}}\)
Solution:

Question 3.
Prove that r(r₁ + r₂ + r₃) = ab + bc + ca – s².
Solution:

Question 4.
Show that \(\sum \frac{r_{1}}{(s-b)(s-c)}=\frac{3}{r}\)
Solution:

Question 5.
Show that \(\left(r_{1}+r_{2}\right) \tan \frac{C}{2}=\left(r_{3}-r\right) \cot \frac{C}{2}=c\)
Solution:

Question 6.
Show that r₁r₂r₃ = \(r^{3} \cot ^{2} \frac{A}{2} \cdot \cot ^{2} \frac{B}{2} \cdot \cot ^{2} \frac{C}{2}\)
Solution:

III.

Question 1.
Show that cos A + cos B + cos C = 1 + \(\frac{r}{R}\)
Solution:
L.H.S = cos A + cos B + cos C
= 2 cos(\(\frac{A+B}{2}\)) cos(\(\frac{A-B}{2}\)) + cos C

Question 2.
Show that \(\cos ^{2} \frac{A}{2}+\cos ^{2} \frac{B}{2}+\cos ^{2} \frac{C}{2}=2+\frac{r}{2 R}\)
Solution:

Question 3.
Show that \(\sin ^{2} \frac{A}{2}+\sin ^{2} \frac{B}{2}+\sin ^{2} \frac{C}{2}=1-\frac{r}{2 R}\)
Solution:

Question 4.
Show that
(i) a = (r₂ + r₃) \(\sqrt{\frac{r r_{1}}{r_{2} r_{3}}}\)
(ii) ∆ = r₁r₂ \(\sqrt{\frac{4 R-r_{1}-r_{2}}{r_{1}+r_{2}}}\)
Solution:

Question 5.
Prove that \(r_{1}^{2}+r_{2}^{2}+r_{3}^{2}+r^{2}\) = 16R² – (a² + b² + c²).
Solution:

Question 6.
If p₁, p₂, p₃ are altitudes drawn from vertices A, B, C to the opposite sides of a triangle respectively, then show that
(i) \(\frac{1}{p_{1}}+\frac{1}{p_{2}}+\frac{1}{p_{3}}=\frac{1}{r}\)
(ii) \(\frac{1}{p_{1}}+\frac{1}{p_{2}}-\frac{1}{p_{3}}=\frac{1}{r_{3}}\)
(iii) p₁ . p₂ . p₃ = \(\frac{(a b c)^{2}}{8 R^{3}}=\frac{8 \Delta^{3}}{a b c}\)
Solution:

Question 7.
If a = 13, b = 14, c = 15, show that R = \(\frac{65}{8}\), r = 4, r₁ = \(\frac{21}{2}\), r₂ = 12 and r₃ = 14.
Solution:
a = 13, b = 14, c = 15
s = \(\frac{a+b+c}{2}\)
= \(\frac{13+14+15}{2}\)
= 21
s – a = 21 – 13 = 8
s – b = 21 – 14 = 7
s – c = 21 – 15 = 6

Question 8.
If r₁ = 2, r₂ = 3, r₃ = 6 and r = 1, prove that a = 3, b = 4 and c = 5.
Solution:

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Properties of Triangles Solutions Exercise 10(a)

All problems in this exercise refer to ΔABC

I.

Question 1.
Show that Σa(sin B – sin C) = 0
Solution:

Question 2.
If a = √3 + 1 cms, ∠B = 30°, ∠C = 45°, then find c.
Solution:
∠B = 30°, ∠C = 45° and a = (√3 + 1) cms
A = 180° – (B + C)
= 180° – (30° + 45°)
= 180° – 75°
= 105°

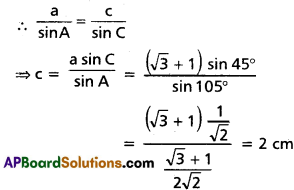
Question 3.
If a = 2 cms, b = 3 cms, c = 4 cms, then find cos A.
Solution:
a = 2 cms, b = 3 cms and c = 4 cms

Question 4.
If a = 26 cms, b = 30 cms and cos C = \(\frac{63}{65}\), then find c.
Solution:
a = 26 cms, b = 30 cms and cos C = \(\frac{63}{65}\)
c² = a² + b² – 2ab cos C
⇒ c² = 676 + 900 – 2 × 26 × 30 × \(\frac{63}{65}\)
⇒ c² = 1576 – 1512
⇒ c² = 64
⇒ c = 8

Question 5.
If the angles are in the ratio 1 : 5 : 6, then find the ratio of its sides.
Solution:
Given \(\frac{A}{1}=\frac{B}{5}=\frac{C}{6}\), B = 5A, C = 6A
A + B + C = 180°
⇒ A + 5A + 6A = 180°
⇒ 12A = 180°
⇒ A = 15°
∴ B = 5A = 75°
∴ C = 6A = 90°
a : b : c = sin A : sin B : sin C
= sin 15° : sin 75° : sin 90°
= \(\frac{\sqrt{3}-1}{2 \sqrt{2}}: \frac{\sqrt{3}+1}{2 \sqrt{2}}: 1\)
= (√3 – 1) : (√3 + 1) : 2√2

Question 6.
Prove that 2(bc cos A + ca cos B + ab cos C) = a² + b² + c².
Solution:
L.H.S = Σ2bc cos A
= Σ2bc \(\frac{\left(b^{2}+c^{2}-a^{2}\right)}{2 b c}\)
= Σ(b² + c² – a²)
= b² + c² – a² + c² + a² – b² + a² + b² – c²
= a² + b² + c²
= R.H.S

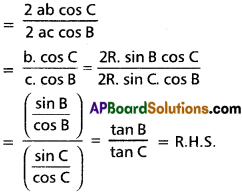
Question 7.
Prove that \(\frac{a^{2}+b^{2}-c^{2}}{c^{2}+a^{2}-b^{2}}=\frac{\tan B}{\tan C}\)
Solution:
L.H.S = \(\frac{a^{2}+b^{2}-c^{2}}{c^{2}+a^{2}-b^{2}}=\frac{\tan B}{\tan C}\)
[∵ c² = a² + b² – 2ab cos C and b² = a² + c² – 2ac cos B]

Question 8.
Prove that (b + c) cos A + (c + a) cos B + (a + b) cos C = a + b + c
Solution:
L.H.S = (b + c) cos A + (c + a) cos B + (a + b) cos C
= (b cos A + c cos A) + (c cos B + a cos B) + (a cos C + b cos C)
= (b cos C + c cos B) + (a cos C + c cos A) + (a cos B + b cos A)
= a + b + c
= R.H.S

Question 9.
Prove that (b – a cos C) sin A = a cos A sin C
Solution:
LHS = (b – a cos C) sin A
= (a cos C + c cos A – a cos C) sin A
= c cos A sin A [∵ b = a cos C + c cos A]
= (2R sin C) cos A sin A
= a cos A sin C (∵ 2R sin A = a)

Question 10.
If 4, 5 are two sides of a triangle and the included angle is 60°, find its area.
Solution:
Let a = 4, b = 5 are two sides and included angle is C = 60° then
Area of ∆ = \(\frac{1}{2}\) ab sin C
= \(\frac{1}{2}\) × 4 × 5 × sin 60°
= 2 × 5 × \(\frac{\sqrt{3}}{2}\)
= 5√3 sq.cm

Question 11.
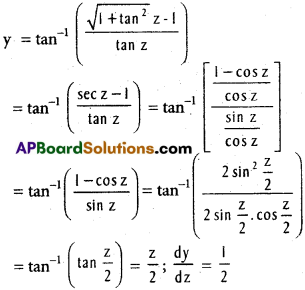
Show that \(b \cos ^{2} \frac{C}{2}+c \cos ^{2} \frac{B}{2}=s\)
Solution:

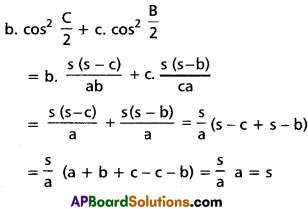
Question 12.
If \(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}\), then show that ∆ABC is equilateral.
Solution:
Given that \(\frac{a}{\cos A}=\frac{b}{\cos B}=\frac{c}{\cos C}\)
⇒ \(\frac{2 R \sin A}{\cos A}=\frac{2 R \sin B}{\cos B}=\frac{2 R \sin C}{\cos C}\)
⇒ \(\frac{\sin A}{\cos A}=\frac{\sin B}{\cos B}=\frac{\sin C}{\cos C}\)
⇒ tan A = tan B = tan C
⇒ A = B = C
⇒ ∆ABC is an equilateral triangle.

II.

Question 1.
Prove that a cos A + b cos B + c cos C = 4R sin A sin B sin C.
Solution:
L.H.S = (2R sin A) cos A + (2R sin B) cos B + (2R sin C) cos C
= R (sin 2A + sin 2B + sin 2C)
= R (2 sin (A + B) cos (A – B) + sin 2C)
= R [2 sin (180° – C) cos (A – B) + sin 2C]
= R (2 sin C . cos (A – B) + 2 sin C . cos C)
= 2R sin C (cos (A – B)) + cos C)
= 2R sin C (cos (A – B) + cos (180° – \(\overline{\mathrm{A}+\mathrm{B}}\))
= 2R sin C [cos (A – B) – cos (A + B)]
= 2R sin C (2 sin A sin B)
= 4R sin A sin B sin C
= R.H.S.

Question 2.
Prove that Σa³ sin(B – C) = 0.
Solution:
L.H.S = Σa² [a sin (B – C)]
= Σa² [2R . sin A sin (B – C)]
= R Σ a² (2 sin (180° – \(\overline{\mathrm{B}+\mathrm{C}}\)) sin (B – C))
= R Σ a² [2 sin (B + C) . sin (B – C)]
= R Σ a² (sin² B – sin² C)
= R Σ a² \(\left(\frac{b^{2}}{4 R^{2}}-\frac{c^{2}}{4 R^{2}}\right)\)
= \(\frac{1}{2 R}\) Σ[a² (b² – c²)]
= \(\frac{1}{2 R}\) a² (b² – c²) + b² (c² – a²) + c² (a² – b²)]
= \(\frac{1}{2 R}\) (a²b² – a²c² + b²c² – a²b² + a²c² – b²c²)
= \(\frac{1}{2 R}\) × 0
= 0
= R.H.S

Question 3.
Prove that \(\frac{a \sin (B-C)}{b^{2}-c^{2}}=\frac{b \sin (C-A)}{c^{2}-a^{2}}=\frac{c \sin (A-B)}{a^{2}-b^{2}}\)
Solution:

Question 4.
Prove that \(\sum a^{2} \frac{a^{2} \sin (B-C)}{\sin B+\sin C}=0\)
Solution:

Question 5.
Prove that \(\frac{a}{b c}+\frac{\cos A}{a}=\frac{b}{c a}+\frac{\cos B}{b}=\frac{c}{a b}+\frac{\cos C}{c}\)
Solution:

Question 6.
Prove that \(\frac{1+\cos (A-B) \cos C}{1+\cos (A-C) \cos B}=\frac{a^{2}+b^{2}}{a^{2}+c^{2}}\)
Solution:

Question 7.
If C = 60°, then show that
(i) \(\frac{\mathbf{a}}{\mathbf{b}+\mathbf{c}}+\frac{\mathbf{b}}{\mathbf{c}+\mathbf{a}}=1\)
(ii) \(\frac{b}{c^{2}-a^{2}}+\frac{a}{c^{2}-b^{2}}=0\)
Solution:
∠C = 60°
⇒ c² = a² + b² – 2ab cos C
⇒ c² = a² + b² – 2ab cos 60°
⇒ c² = a² + b² – 2ab (\(\frac{1}{2}\))
⇒ c² = a² + b² – ab

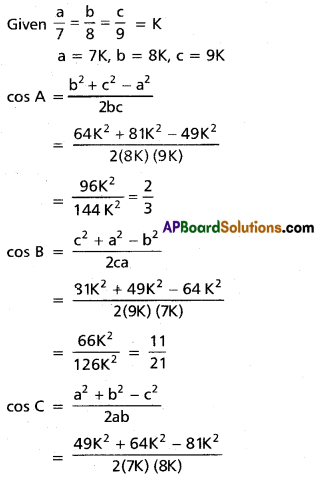
Question 8.
If a : b : c = 7 : 8 : 9, find cos A : cos B : cos C.
Solution:

Question 9.
Show that \(\frac{\cos A}{a}+\frac{\cos B}{b}+\frac{\cos C}{c}=\frac{a^{2}+b^{2}+c^{2}}{2 a b c}\)
Solution:

Question 10.
Prove that (b – a) cos C + c (cos B – cos A) = c . sin(\(\frac{A-B}{2}\)) cosec(\(\frac{A+B}{2}\))
Solution:
L.H.S = b cos C – a cos C + c cos B – c cos A
= (b cos C + c cos B) – (a cos C + c cos A)
= a – b
= 2R (sin A – sin B)

Question 11.
Express \(a \sin ^{2} \frac{C}{2}+c \cdot \sin ^{2} \frac{A}{2}\) interms of s, a, b, c.
Solution:

Question 12.
If b + c = 3a, then rind the value of \(\cot \frac{\mathrm{B}}{2} \cot \frac{\mathrm{C}}{2}\)
Solution:

Question 13.
Prove that (b + c) cos (\(\frac{B+C}{2}\)) = a cos (\(\frac{B-C}{2}\))
Solution:

Question 14.
In ΔABC, show that \(\frac{b^{2}-c^{2}}{a^{2}}=\sin \frac{(B-C)}{(B+C)}\)
Solution:

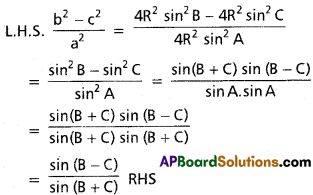
III.

Question 1.
Prove that
(i) \(\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}=\frac{s^{2}}{\Delta}\)
(ii) \(\tan \frac{A}{2}+\tan \frac{B}{2}+\tan \frac{C}{2}\) = \(\frac{b c+c a+a b-s^{2}}{\Delta}\)
(iii) \(\frac{\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}}{\cot A+\cot B+\cot C}\) = \(\frac{(a+b+c)^{2}}{a^{2}+b^{2}+c^{2}}\)
Solution:

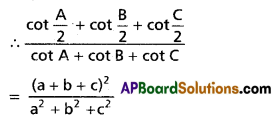
Question 2.
Show that
(i) Σ(a + b) tan(\(\frac{A-B}{2}\)) = 0
(ii) \(\frac{\mathbf{b}-\boldsymbol{c}}{\mathbf{b}+\mathbf{c}} \cot \frac{A}{2}+\frac{b+c}{b-c} \tan \frac{A}{2}\) = 2 cosec(B – C)
Solution:

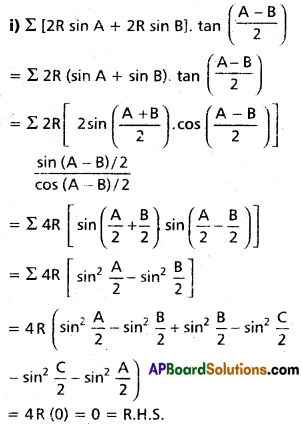
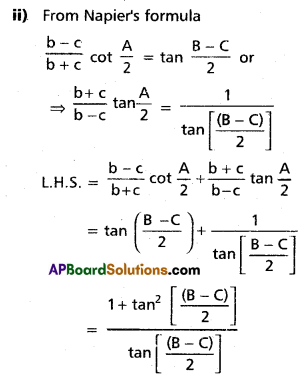
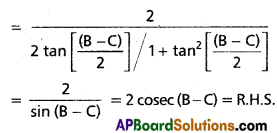
Question 3.
(i) If sin θ = \(\frac{a}{b+c}\), then show that cos θ = \(\frac{2 \sqrt{b c}}{b+c} \cdot \cos \frac{A}{2}\)
Solution:

(ii) If a = (b + c) cos θ, then prove that sin θ = \(\frac{2 \sqrt{b c}}{b+c} \cos \left(\frac{A}{2}\right)\)
Solution:

(iii) For any anlge θ show that a cos θ = b cos (C + θ) + c cos (B – θ).
Solution:
b cos (C + θ) + c cos (B – θ)
= b (cos C . cos θ – sin C sin θ) + c (cos B cos θ + sin B sin θ)
= (b cos C + c cos B) cos θ + (-b sin C + C sin B) sin θ
= a cos θ + (-2R sin B sin C + 2R sin B sin C) sin θ
= a cos θ

Question 4.
If the angles of ∆ABC are in A.P and b : c = √3 : √2 , then show that A = 75°.
Solution:
∵ The angles A, B, C of a triangle are in A.P.
⇒ 2B = A + C
⇒ 3B = A + B + C
⇒ 3B = 180°
⇒ B = 60°

Question 5.
If \(\frac{a^{2}+b^{2}}{a^{2}-b^{2}}=\frac{\sin C}{\sin (A-B)}\), prove that ∆ABC is either isosceles or right-angled.
Solution:

⇒ sin 2A = sin 2B
⇒ A = B
⇒ ∆ABC is isosceles
or 2A = 180° – 2B
or A = 90° – B
or A + B = 90°
so A ≠ B ⇒ ∆ABC is a right-angled triangle
∴ ∆ABC is either isosceles (or) right-angled.

Question 6.
If cos A + cos B + cos C = \(\frac{3}{2}\), then show that the triangle is equilateral.
Solution:

Question 7.
If cos² A + cos² B + cos² C = 1, then show that ∆ABC is right-angled.
Solution:
Given cos² A + cos² B + cos² C = 1 …….(1)
Now cos² A + cos² B + cos² C
= cos² A + 1 – sin² B + cos² C
= 1 + (cos² A – sin² B) + cos² C
= 1 + cos (A + B) cos (A – B) + cos² C
= 1 + cos (180° – C) cos (A – B) + cos² C
= 1 – cos C . cos (A – B) + cos² C
= 1 – cos C (cos (A – B) – cos C)
= 1 – cos C (cos (A – B) – cos (180° – \(\overline{A+B}\)))
= 1 – cos C (cos (A – B) + cos (A + B))
= 1 – cos C (2 cos A cos B)
= 1 – 2 cos A cos B cos C
Substituting in (1) we get
1 – 2 cos A cos B cos C = 1
∴ 2 cos A cos B cos C = 0
∴ cos A = 0 or cos B = 0 or cos C = 0
i.e., A = 90° or B = 90° or C = 90°
∴ ∆ABC is right-angled.

Question 8.
If a² + b² + c² = 8R², then prove that the triangle is right angled.
Solution:
Given a² + b² + c² = 8R²
⇒ 4R² (sin² A + sin² B + sin² C) = 8R²
⇒ sin² A + sin² B + sin² C = 2 ……(1)
Now sin² A + sin² B + sin² C
= 1 – cos² A + sin² B + sin² C
= 1 – (cos² A – sin² B) + sin² C
= 1 – cos (A + B) . cos (A – B) + sin² C
= 1 – cos (180° – C) cos (A – B) + sin² C
= 1 + cos C cos (A – B) + 1 – cos² C
= 2 + cos C (cos (A – B) – cos C)
= 2 + cos C (cos (A – B) – cos (180° – \(\overline{A+B}\)))
= 2 + cos C (cos (A – B) + cos (A + B))
= 2 + cos C (2 cos A cos B)
= 2 + 2 cos A cos B cos C
Substituting in (1), we get
2 + 2 cos A cos B cos C = 2
2 cos A cos B cos C = 0
⇒ cos A = 0 or cos B = 0 or cos C = 0
∴ A = 90° or B = 90° or C = 90°
∴ ΔABC is right-angled.

Question 9.
If cot \(\frac{A}{2}\), cot \(\frac{B}{2}\), cot \(\frac{C}{2}\) are in A.P., then prove that a, b, c are in A.P.
Solution:
∵ cot \(\frac{A}{2}\), cot \(\frac{B}{2}\), cot \(\frac{C}{2}\) are in A.P
⇒ \(\frac{(s)(s-a)}{\Delta}, \frac{(s)(s-b)}{\Delta}, \frac{(s)(s-c)}{\Delta}\) are in A.P.
⇒ s – a, s – b, s – c are in A.P
⇒ -a, -b, -c are in A.P
⇒ a, b, c are in A.P

Question 10.
If \(\sin ^{2} \frac{A}{2}, \sin ^{2} \frac{B}{2}, \sin ^{2} \frac{C}{2}\) are in H.P., show that a, b, c are in H.P.
Solution:

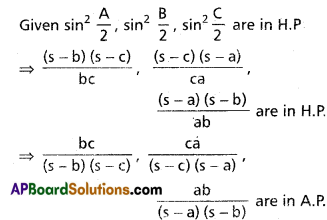
Question 11.
If C = 90° then prove that \(\frac{a^{2}+b^{2}}{a^{2}-b^{2}}\) sin (A – B) = 1
Solution:

Question 12.
Show that \(\frac{a^{2}}{4} \sin 2 C+\frac{c^{2}}{4} \sin 2 A\) = ∆
Solution:
LHS = \(\frac{a^{2}}{4} \sin 2 C+\frac{c^{2}}{4} \sin 2 A\)
= \(\frac{4 R^{2} \sin ^{2} A}{4}\) 2 sin C cos C + \(\frac{4 R^{2} \sin ^{2} C}{4}\) 2 sin A cos A
= 2R² sin²A sin C cos C + 2R² sin²C sin A cos A
= 2R² sin A sin C (sin A cos C + cos A sin C)
= 2R² sin A sin C sin(A + C)
= 2R² sin A sin C sin(180 – B)
= 2R² sin A sin B sin C
= ∆
= RHS

Question 13.
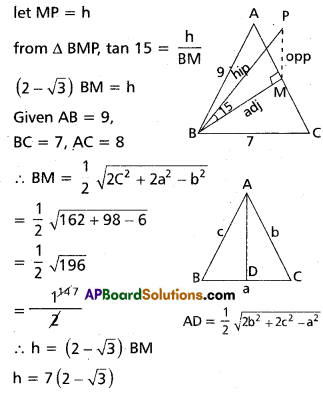
A lamp post is situated at the middle point I the side AC of a triangular plot A with BC = 7 meters, CA = 8 meters, and AB = 9 meters, lamp post subtends an angle of 15° at point B. find H height of the lamp post.
Solution:
Let MP be the height of the lamp post

Question 14.
Two ships leave a port at the same time. One goes 24 km. per hour in the direction N45°E and other travels 32 km per hour in the direction S75°E. Find the distance between the ships at the end of 3 hours.
Solution:
Given the first ship goes 24 km per hour After 3 hours the first ship goes 72 km.

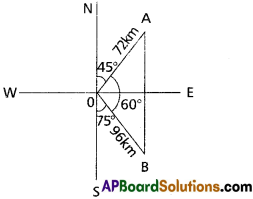
Given the second ship goes 32 km per hour After 3 hours, the second ship goes 96 km.
Let AB = x
∠AOB = 180° – (75 + 45) = 60°
Apply cosine rule for ∆AOB,
cos 60° = \(\frac{(72)^{2}+(96)^{2}-x^{2}}{2(72)(96)}\)
⇒ \(\frac{1}{2}=\frac{5184+9216-x^{2}}{13824}\)
⇒ 13824 = 28800 – 2x²
⇒ 2x² = 14976
⇒ x² = 7488
⇒ x = 86.4 (Appx)
At the end of 3 hours the difference between ships was 86.4 km.

Question 15.
A tree stands vertically on the slant of the hill. From A point on the ground 35 meters down the hill from the base of the tree, the angle, the elevation of the top of the tree is 60° if the angle of elevation of the foot of the tree from A is 15°, then find the height of the tree.
Solution:
Let BC be the height of the tree
BC = h
Let BD = x, AD = y
Given AB = 35 m

Question 16.
The upper \(\frac{3}{4}\)th portion of a vertical pole subtends an angle tan-1(\(\frac{3}{5}\)) at a point in the horizontal plane through its foot and at a distance 40 m from the foot. Given that the vertical pole is at a height less than 100 m from the ground, find its height.
Solution:

⇒ 6400 + h² = 200h
⇒ h² – 200h + 6400 = 0
⇒ h² – 160h – 40h + 6400 = 0
⇒ h(h – 160) – 40(h – 160) = 0
⇒ (h – 160) (h – 40) = 0
⇒ h = 40 or 160
but the height of the pole should be less than 100m
∴ h = 40 m

Question 17.
AB is a vertical pole with B at the ground level and A at the top. A man finds that the angle of elevation of point A from a certain point C on the ground is 60°. He moves away from the pole along the line BC to a point D such that CD = 7 m. From D, the angle of elevation of point A is 45°. Find the height of the pole.
Solution:
Let ‘h’ be the height of the pole
AB = h
given CD = 7 m
∠ACB = 60°, ∠ADB = 45°, Let BC = x

Question 18.
Let an object be placed at some height h cm and let P and Q two points of observation which are at a distance of 10 cm apart on a line inclined at an angle of 15° to the horizontal. If the angles of elevation of the object from P and Q are 30° and 60° respectively then find h.
Solution:
Let AB = Height of the object from ‘A’ = h m
Given that P & Q are two observations,
PQ = 10 cms

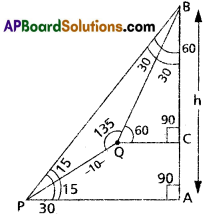
From ∆APB,
∠P = 30; ∠A = 90; ∠B = ?
A + P + B = 180°
⇒ 30° + 30° + B = 180°
⇒ B = 180° – 120°
⇒ B = 60°
From ∆BQC,
∠Q = 60°; ∠C = 90°; ∠B = ?
Q + C + B = 180°
⇒ 60° + 90° + B = 180°
⇒ B = 180° – 150°
⇒ B = 30°
From ∆BQP,
∠P = 15; ∠B = 30; ∠Q = ?
P + B + Q = 180°
⇒ 15° + 30° + Q = 180°
⇒ Q = 180° – 45°
⇒ Q = 135°
Applying the ‘sin’ rule for ∆BQP

From ∆PAB,
sin 30° = \(\frac{B A}{B P}\)
BP . sin 30° = AB = h
√2 × 10 × \(\frac{1}{2}\) = AB = h
5√2 = AB = h
∴ h = 5√2

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Differentiation Solutions Exercise 9(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Differentiation Solutions Exercise 9(a)

I. Compute the following limits.

Question 1.
Find the derivatives of the following func-tions f(x). 7286883416
i) \(\sqrt{x}+2 x^{\frac{3}{4}}+3 x^{\frac{5}{6}}\) (x > 0)
Solution:
y = \(\sqrt{x}+2 x^{\frac{3}{4}}+3 x^{\frac{5}{6}}\) (x>0)
\(\frac{dy}{dx}\) = \(\frac{1}{2}\).x^-1/2 + 2.\(\frac{3}{4}\).x^-1/4 + 3.\(\frac{5}{6}\).^x-1/6 dx
= \(\frac{1}{2}\)[x^-1/2 + 3.x^-1/4 + 5.x^-1/6]

ii) \(\sqrt{2 x-3}+\sqrt{7-3 x}\).
Solution:

iii) (x² – 3) (4x³ + 1)
Solution:
y = (x² – 3) (4x³ + 1)
\(\frac{dy}{dx}\) = (x² – 3) \(\frac{d}{dx}\) (4x³ + 1) + (4x³ + 1) \(\frac{d}{dx}\)(x² – 3)
= (x² – 3) (12x²) + (4x³ + 1) (2x)
= 12x⁴ – 36x² + 8x⁴ + 2x
= 20x⁴ – 36x² + 2x

iv) (√x – 3x) (x + \(\frac{1}{x}\))
Solution:
y = (√x – 3x) (x + \(\frac{1}{x}\))

v) (√x + 1) (x² – 4x + 2) (x > 0)
Solution:
y = (√x + 1) (x² – 4x + 2) (x > 0)
Differentiating w.r.to x
\(\frac{dy}{dx}\) = (√x + 1) \(\frac{d}{dx}\)(x² – 4x + 2) + (x² – 4x + 2) \(\frac{d}{dx}\)(√x +1)
= (√x + 1) (2x – 4) + \(\frac{x^{2}-4 x+2}{2 \sqrt{x}}\)

vi) (ax + b)ⁿ. (cx + d)^m.
Solution:
y = (ax + b)ⁿ. (cx + d)^m
\(\frac{dy}{dx}\) = (ax + b)ⁿ \(\frac{d}{dx}\)(cx +d)^m + (cx + d)^m \(\frac{d}{dx}\)(ax + b)ⁿ
= (ax + b)ⁿ [m(cx + d)^m-1. c] + (cx + d)^m [n(ax + b)^n-1. a]
= (ax + b)^n-1 (cx + d)^m-1 [cm (ax + b) + an (cx + d)]
= (ax + b)ⁿ (cx + d)^m [\(\frac{an}{ax+b} + \frac{cm}{cx+d}\) ]

vii) 5 sin x + ex log x
Solution:
y = 5 sin x + e^x. log x
\(\frac{dy}{dx}\) = 5 cos x + e^x. \(\frac{d}{dx}\) (log x) + log x \(\frac{d}{dx}\)(e^x)
= 5 cos x + e^x. \(\frac{1}{x}\) + (log x) (e^x)

viii) 5^x + log x + x³ e^x
Solution:
y = 5^x + log x + x³ e^x
\(\frac{dy}{dx}\) = 5^x . log 5 + \(\frac{1}{x}\) + x³.e^x + e^x.3x²
= 5^x. log 5 + – + x³ e^x + 3x² e^x

ix) e^x + sin x cos x
Solution:
y = e^x + sin x . cos x
\(\frac{dy}{dx}\) = \(\frac{d}{dx}\) (e^x) + \(\frac{d}{dx}\) (sin x . cos x)
= e^x + sin x \(\frac{d}{dx}\) (cos x) + cos x \(\frac{d}{dx}\) (sin x)
= e^x – sin² x + cos² x
= e^x + cos 2x

x) \(\frac{p x^{2}+e x+r}{a x+b}\)(|a| + |b| ≠ 0)
Solution:

xi) log₇ (log x) (x > 0)
Solution:
y = log₇ (log x) (x > 0)

xii) \(\frac{1}{a x^{2}+b x+c}\) (|a| + |b| + |c| ≠ 0)
Solution:
\(\frac{1}{a x^{2}+b x+c}\) (|a| + |b| + |c| ≠ 0)

xiii) e^2x log (3x + 4) (x > –\(\frac{4}{3}\))
Solution:
y = e^2x. log (3x + 4) (x > –\(\frac{4}{3}\))
Differentiating w.r.to x
\(\frac{dy}{dx}\) = e^2x \(\frac{d}{dx}\)[log (3x + 4) + log (3x + 4) \(\frac{d}{dx}\) (e^2x)]
= e^2x.\(\frac{1}{3x+4}\) 3 + log (3x + 4). e^2x . 2
= e^2x (\(\frac{3}{3x+4}\) + 2 log (3x + 4))

xiv) (4 + x²) e²xy
Solution:
y = (4 + x²). e^2x
Differentiating w.r.to x
\(\frac{dy}{dx}\) = (4 + x²) \(\frac{d}{dx}\) (e^2x) + e^2x \(\frac{d}{dx}\)(4 + x²)
= (4 + x²). 2e^2x + e^2x (0 + 2x)
= 2e^2x [4 + x² + x]
= 2e^2x (x² + x + 4)

xv) \(\frac{ax+b}{cx+d}\) [|c| + |d|≠0]
Solution:
y = \(\frac{ax+b}{cx+d}\) [|c| + |d|≠0]
Differentiating w.r.to x

xvi) a^x. e^x²
Solution:
y = a^x. e^x²
Differentiating w.r.to x
\(\frac{dy}{dx}\) = (a^x) \(\frac{d}{dx}\)(e^x²) + (e^x²)\(\frac{d}{dx}\)(a^x)
= a^x. e^x². 2x + e^x². a^x. log a
= ax. ^x² (2x + log a)
= y(2x + log a)

Question 2.
If f(x) = 1 + x + x² + + x¹⁰⁰, then find f’ (1).
Solution:
f'(x) = 1 + 2x + 3x² + 100 x⁹⁹
f'(1) = 1+2 + 3 ….+ 100
= \(\frac{100 \times 101}{2}=5050\left(\Sigma x=\frac{x(x+1)}{2}\right)\)

Question 3.
If f (x) = 2x² + 3x – 5, then prove that f(0) + 3f (-1) = 0.
Solution:
f'(x) = 4x + 3
f'(0) = 0 + 3 = 3
f'(-1) = – 4 + 3 = -1
f'(0) + 3f'(-1) = 3 + 3(-1) = 3 – 3 = 0 n.

II.

Question 1.
Find the derivatives of the following functions from the first principles.
i) x³
Solution:


= 3x² + 0 + 0 = 3x²

ii) x⁴ + 4
Solution:
f(x + h) – f(x) = ((x + h)⁴ + 4) – (x⁴ + 4)
= (x + h)4 + 4 – x⁴ – 4 .
= x⁴ + 4x³h + 6x²h² + 4xh³ + h⁴ – x⁴

= 4x³ + 0 + 0 + 0 = 4x³

iii) ax² + bx + c
Solution:
f(x + h) = a(x + h)² + b(x + h) + c
= a(x² + 2hx + h²) + b(x + h) + c
= ax² + 2ahx + ah² + bx + bh +c

f(x + h) – f(x) = ax² + 2ahx + ah² + bx + bh + c – ax² – bx – c
= h [2ax + ah + b]

= 2ax + 0 + b = 2ax + b

iv) \(\sqrt{x+1}\)
Solution:

v) sin 2x
Solution:
f(x + h) – f(x) = sin 2(x + h) – sin 2x

vi) cos ax
Solution:
f(x + h) – f(x) = cos a (x + h) – cos ax

= – 2 sin ax. \(\frac{a}{2}\)
=-a. sin ax

vii) tan 2x
Solution:
f(x + h) – f(x) = tan 2(x + h) – tan 2x

viii) cot x
Solution:
f(x + h) – f(x) = cot (x + h) – cot x

ix) sec 3x
Solution:
f(x + h) – f(x)= sec 3(x + h) – sec 3x

x) x sin x
Solution:
f(x + h) – f(x) = (x + h) sin (x + h) – x sin x
= x (sin (x + h) – sin x) + h. sin (x + h)

xi) cos² x
Solution:
f(x + h) – f(x) = cos² (x + h) – cos² x
= -(cos² x – cos² (x + h))
= -sin (x + h + x) sin (x + h – x)

= -sin 2x. 1 = -sin 2x

Question 2.
Find the derivatives of the following function.
i) \(\frac{1-x \sqrt{x}}{1+x \sqrt{x}}\) (x > 0)
Solution:

ii) xⁿ n^x log (nx) (x > 0, n ∈ N)
Solution:
y = xⁿ. n^x. log nx
\(\frac{dy}{dx}\) = xⁿ. n^x (log nx) + nⁿ. log xn (xⁿ) + xⁿ. log nx (n^x)
= xⁿ. n^x \(\frac{n}{log nx}\) + n^x. log xⁿ (nx^n-1) + xⁿ . log nx. (n^x . log nx)
= x^n-1. n^x[\(\frac{nx}{log nx}\) + log nx. (nⁿ. log nx)]

iii) ax²ⁿ. log x + bxⁿ e^-x
Solution:
y = ax²ⁿ. log x + bxⁿ e^-x
\(\frac{dy}{dx}\) = a (x²ⁿ.\(\frac{1}{x}\) + log x (2nx^2n-1)) + b n (-e^-x) + e^-x. nx^n-1)
= a. x^2n-1 + 2an. x^2n-1. log x – bxⁿ e^-x + bn. x^n-1 . e^-x

iv) (\(\frac{1}{x}\) – x)³ e^x
Solution:
y = (\(\frac{1}{x}\) – x)³ . e^x
\(\frac{dy}{dx}\) = (\(\frac{1}{x}\) – x)³ \(\frac{d}{dx}\)(e^x) + e^x \(\frac{d}{dx}\){(\(\frac{1}{x}\) – x)³}

Question 3.
Show that the function f(x) = |x| + |x – 1|, x ∈ R is differentiable for all real numbers except for 0 and 1.
Solution:
f(x) = |x| + |x – 1| ∀ x ∈ R
f(x) = x + x – 1 = 2x – 1, x ≥ 1
= x – (x – 1) = x – x + 1, = 1, 0 < x < 1
= -x – (x – 1) =-x – x + 1 = 1 – 2x, x < 0 ∴ f(x) = 2x – 1, x > 1
= 1, 0 < x < 1 = 1 – 2x, x ≤ 0 If x > 1, then f(x) = 2x – 1 = polynomial in x f(x) is differentiable for all x > 1
If 0 < x < 1, then f(x) = 1 – constant
∴ f(x) is differentiable if 0 < x < 1.
If x < 1, then f(x) = 1 – 2x = polynomial in x.
∴ f(x) is differentiable for all x < 1

Case (i) : x = 0

R f'(0) ≠ Lf'(0)
∴ f'(0) does not exist.
f(x) is not differentiable at x = 0.

Case (ii): x = 1

R f'(1) ≠ L f'(1)
f(1) does not exist.
f(x) is not differentiable at x = 1
∴ f(x) is differentiable for all real x except zero and one.

Question 4.
Verify whether the following function is differentiable at 1 and 3.

Solution:
Case (i): x = 1

R f'(1) ≠ L f'(1)
f(x) is not differentiable at x = 1

Case (ii) : x = 3

f(3⁺) ≠ f'(3^–)
f(x) is not differentiable at x = 3.

Question 5.
Is the following function f derivable at 2?

Solution:

f'(2^–) ≠ f(2⁺); f(x) is not derivable at x = 2.

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(a) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Limits and Continuity Solutions Exercise 8(a)

I. Compute the following limits.

Question 1.

Solution:

Question 2.

Solution:

Question 3.

Solution:

Question 4.

Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.

Solution:

Question 9.

Solution:

Question 10.

Solution:

Question 11.

Solution:

Question 12.

Solution:

Question 13.

Note : Text Book answer will come, when the problem changes like.
Solution:

Question 14.

Solution:

Question 15.

Solution:

Question 16.

Solution: