AP Inter 1st Year Chemistry Notes Chapter 1 Atomic Structure

Students can go through AP Inter 1st Year Chemistry Notes 1st Lesson Atomic Structure will help students in revising the entire concepts quickly.

AP Inter 1st Year Chemistry Notes 1st Lesson Atomic Structure

→ Cathode rays consist of negatively charged particles called Electrons.

→ Charge to mass ratio (e/m) of electron is 1.758820 × 10¹¹ c.kg^-1.

→ A stream of positively charged particles in modified cathode ray tube are called canal rays or protons.

→ Rutherford’s model resembles the solar system. The positive charge at the centre is called nucleus and electrons move around it in circular paths are called the orbits.

→ Rutherford model does not explain the electronic structure of the atoms.

→ Light is an electromagnetic radiation. The characteristics of wave motion are wavelength, wave number, frequency, velocity and amplitude.

→ Planck’s quantum theory states that radiation is absorbed or emitted by a body in quanta, which propagates in the form of waves. The energy of radiation E = hν.

→ Line spectrum is characteristic to gaseous atoms. Band spectrum is characteristic to gaseous molecules.

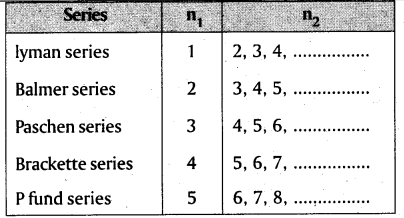
→ Atomic spectrum of hydrogen consists of Lyman series (UV region); Balmer series (visible region); Paschen, Brackett and P fund series (infra red region).

→ The wave number of lines can be expressed by Rydberg’s equation.
\(\bar{v}=\frac{1}{\lambda}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)

→ Bohr’s model of atom : Electrons revolve round the nucleus in stationary orbits with constant energy given by the principal quantum number.
Emission or absorption of energy by electron will be in quanta. While doing so, the electron jumps from one orbit to another.
The energy of the radiation emitted or absorbed is equal to the difference in the energies of the two orbits.
∆E = E₂ – E₁ = hν.

→ The splitting up of spectral lines when an atom is subjected to strong magnetic field is called Zeeman effect.

→ The splitting up of spectral lines when an atom is subjected to strong electric field is called Stark effect.

→ Quantum numbers: Principal quantum number (n) was proposed by Bohr. It reveals the size of the atom (energy level). Azimuthal quafritum number (l) was proposed by Sommerfeld.
It shows the shape of orbitals. Magnetic quantum number (m) was proposed by Lande. It gives the orientation of the orbit. Spin quantum number (s) was proposed by Uhlenbeck and Goudsmit. It shows the spin of the electron.

→ “No two electrons in an atom will have the values for all the four quantum numbers alike, they may have three quantum numbers alike but not spin quantum number”- this is Paulis exclusion principle.

→ It is impossible to locate the exact position and momentum of a moving electron simultaneously and accurately – this is Heisenberg’s uncertainty principle.

→ Shapes of orbitals – ‘s’ orbital has spherically symmetrical shape, ‘p’ orbital has dumb-bell;-d’ orbital has double dumb-bell, ‘f’ orbital has triple dumb-bell (complex in nature) shape.

→ In the building up of anatom the electron will occupy an available orbital of lowest energy – this is Auf-bau principle.

→ Whenever degenerate orbitals are available for filling – the pairing of electrons takes place only when the degenerate orbitals are half filled – this is Hund’s rule.

→ Lower the value of (n + l) for an orbital, the lower is its energy.

→ Schrodingerwave equation is \(\frac{\partial^2 \Psi}{\partial \mathrm{x}^2}+\frac{\partial^2 \Psi}{\partial \mathrm{y}^2}+\frac{\partial^2 \Psi}{\partial \mathrm{z}^2}+\frac{8 \pi^2 \mathrm{~m}}{\mathrm{~h}^2}(\mathrm{E}-\mathrm{V}) \Psi=0\)

→ Ψ is the wave function but Ψ² denotes the probability of finding an electron in the space around the nucleus.

→ From the value of |Ψ|² at different points within the atom, it is possible to predict the region around the nucleus where electron will most probably be found.

→ For s – orbitals, l = 0 and Ψ = f(r)
For p – orbitals, l = 1 and Ψ_x = f(r) f(x)
Ψ_y = f(r) f(y)
Ψ_z = f(r) f(z)
For d_xy – orbitals, l = 2 and Ψ = f(r) f(x) f(y).

→ Radial nodes are given by (n – l – 1).

→ The surface at which the probability of finding an electron is zero is called a radial node.

→ Electron radial probability distribution function (D) = 4πr²drΨ²

→ According to quantum mechanical model of the atom, the electron distribution of an atom, containing a number of electrons is divided into shells.

→ Half filled and completely filled shells are more stable.

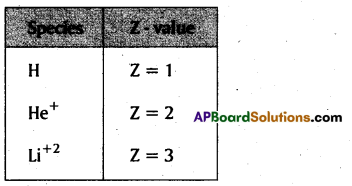
→ Ryd berg’s equation is \(\bar{v}=\frac{1}{\lambda}=R_H Z^2\left[\frac{1}{\mathrm{n}_1^2}-\frac{1}{\mathrm{n}_2^2}\right] \mathrm{cm}^{-1}\)
Z = Atomic number
R_H; = 1,09,677 cm^-1
\(\vec{v}\) = Wave number
λ = Wave length

→ The maximum number ofspactral lines possible = Σ (n – 1)

→ The number of spectral lines formed when an electron jump from n^th orbit to ground state = \(\frac{n(n-1)}{2}\)

→ In the net change in energy ∆E = Σ_n2 – Σ_n1
If n₂ > n₁ then S mission spectra obtained
n₁ > n₂ then obsorption spectra obtained

→ The radius of n^th orbit is
r_n = 0.529 × \(\frac{n^2}{\mathrm{Z}}\)Å
Formula -1
\(\frac{r_1}{r_2}=\frac{n_1^2}{n_2^2}\)

Formula – 2
\(\frac{r_1}{r_2}=\frac{Z_2}{Z_1}\)

→ Potential energy of electron = \(\frac{-\mathrm{Zc}^2}{\mathrm{r}}\)
Kinetic energy (KE) = –\(\frac{1}{2}\) × Potential energy
Total energy = – Kinetic energy
Potential energy = 2 × Total energy

→ Energy of electron E = \(\frac{-13.6 \times \mathrm{Z}^2}{\mathrm{n}^2}\) ev
If Z is constant E.α \(\frac{-1}{n^2} \Rightarrow \frac{E_1}{E_2}=\frac{n_2^2}{n_1^2}\)
If n is constant E_nα – Z²
\(\frac{\mathrm{E}_1}{\mathrm{E}_2}=\frac{\mathrm{Z}_1^2}{\mathrm{Z}_2^2}\)

→ Velocity of electron in n^th orbit (v_n)
v_n = \(\frac{2 \pi \mathrm{e}^2 \mathrm{Z}}{\mathrm{n}^{\mathrm{h}}}\)
= 2.18 × 10⁸ × \(\frac{\mathrm{Z}}{\mathrm{n}}\) cm/sec

→ For a given energy level ‘n’
a) Maximum no. of orbitaly = n²
b) Maximum no. of electrons = 2n²

→ Total spin is given by ±\(\frac{n}{2}\)
n = no. of unpaired electrons

→ Magnetic moment (spin only) μ = \(\sqrt{n(n+2)}\) BM
n = no. of unpaired electrons (BM = Boher Magneton)

→ a) Angular nodes is = l (Azimuthal quantum no.)
b) No. of radial nodes = n – l – 1
c) Total no. of nodes = Angular nodes + radicalnodes
= l + n – l – 1
= n – 1

→ Orbital angular momentum of electron
L = \(\sqrt{l(l+1)} \frac{\mathrm{h}}{2 \pi}\)
l = Azimuthal quantum no

→ Spin angular momentum of electron L_s = \(\sqrt{S(S+1)} \frac{h}{2 \pi}\)

→ Time taken by one revolution of electron = \(\frac{2 \pi r}{v}\)

→ No. of revolutions made by on electron in second = \(\frac{\text { velocity electron }}{\text { circumference of circular orbit }}\)

→ Angular momentum of the electron mvr = \(\frac{\mathrm{nh}}{2 \pi}\)

→ De broglie’s wave length = \(\frac{\mathrm{h}}{\sqrt{2 \mathrm{MeV}}}\)
m = Mass of the particle
e = Charge
v = Stopping potential

→ According to de-broglie for a station any wave
2πr = nλ

→ If E is the kinetic energy of particle then de-broglie’s wave length λ = \(\frac{h}{\sqrt{2 \mathrm{mE}}}\)

→ Shortest wave length is possible for any series if n₂ = α

→ Longest wave length is possible for any series if n₂ = n₁ + 1