Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(c) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(c)
I.
Question 1.
Find the lengths of subtangent and sub-normal at a point of the curve
Solution:
Equation of the curve is y = b. sin \(\frac{x}{a}\)
\(\frac{dy}{dx}\) = b. cos \(\frac{x}{a}.\frac{1}{a}=\frac{b}{a}\). cos \(\frac{x}{a}\)
Length of the sub-tangent = |\(\frac{y_{1}}{f^{\prime}\left(x_{1}\right)}\)|
= \(\frac{b \cdot \sin \frac{x}{a}}{\frac{b}{a} \cdot \cos \frac{x}{a}}=\left|a \cdot \tan \frac{x}{a}\right|\)
Length of the sub-normal = |y1, f'(x1)|
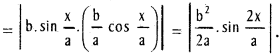
Question 2.
Show that the length of sub normal at any point on the curve xy = a2 varies as the cube of the ordinate of the point.
Solution:
Equation of the curve is xy = a²
y = \(\frac{a^{2}}{x}\)
\(\frac{dy}{dx}=\frac{-a^{2}}{x^{2}}\)
Length of the sub-normal = |y1, f’ (x1)|
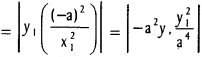
\(\frac{y_{1}^{3}}{a^{2}}\) ∝ y31 = cube of the ordinate.
![]()
Question 3.
Show that at any point (x, y) on the curve y = bex/a, the length of the sub¬tangent is a constant and the length of the sub normal is \(\frac{y^{2}}{a}\).
Solution:
Equation of the curve is y = b.ex/a
\(\frac{a^{2}}{x}\) = b.ex/a.\(\frac{1}{a}=\frac{y}{a}\)
Length of the sub tangent
= |\(\frac{y_{1}}{f^{\prime}\left(x_{1}\right)}\)| = \(\frac{y_{1}}{\left(\frac{y_{1}}{a}\right)}\) = a = constant
Length of the sub-normal
= |y1f'(x1)| = |y1\(\frac{y_{1}}{a}\)| = \(\frac{y_{1}^{2}}{a}\).
II.
Question 1.
Find the value of k so that the length of the sub normal at any point on the curve xyk = ak + 1 is a constant.
Solution:
Equation of the curve is x.yk = ak + 1
Differentiating w.r.to x
x.k.yk-1 \(\frac{dy}{dx}\) + yk.1 = 0
x.k.yk-1 \(\frac{dy}{dx}\) = -yk
\(\frac{dy}{dx}=\frac{-y^{k}}{k \cdot x \cdot y^{k-1}}=-\frac{y}{kx}\)
Length of the sub-normal = |y1f'(x1|

Length of the sub-normal is constant at any point on the curve is independent of x1 and y1
∴ \(\frac{y_{1}^{k+2}}{k \cdot a^{k+1}}\) is independent of x1, y1
⇒ k + 2 = 0 ⇒ k = -2
Question 2.
At any point t on the curve x = a (t + sin t), y = a (1 – cos t), find the lengths of tangent, normal, sub tangent and sub
normal.
Solution:
Equation of the curve is x = a (t + sin t), y = a (1 – cost)
\(\frac{dx}{dt}\) = a (1 + cos t), \(\frac{dy}{dt}\) = a. sin t
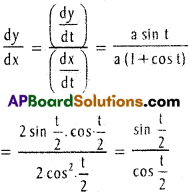
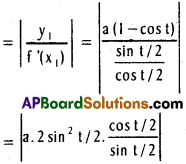
Length of the tangent = |y1|\(\sqrt{1+\frac{1}{\left[f^{\prime}\left(x_{1}\right)\right]^{2}}}\)
Length of the normal = |y1|\(\sqrt{1+\left[f\left(x_{1}\right)\right]^{2}}\)
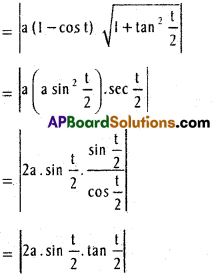
Length of the sub tangent.
= |a (2 sin t/2. cos t/2|
= |a. sin t|
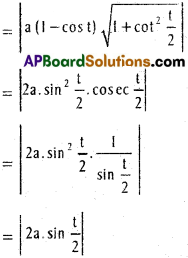
Length of the sub normal
= |y1.f'(x1)| = |a(1 – cos t).\(\frac{\sin t / 2}{\cos t / 2}\)|
= |2a sin² t/2. tan t/2|
= |2a sin² t/2. tan t/2|
![]()
Question 3.
Find the lengths of normal and sub normal at a point on the curve y = \(\frac{a}{2}\) (ex/a + e-x/a).
Solution:
Equation of the curve is y = \(\frac{a}{2}\) (ex/a + e-x/a)
= a. cosh (\(\frac{x}{a}\))
Length of the normal = |y1|\(\sqrt{1+\left[f\left(x_{1}\right)\right]^{2}}\)
= |a.cosh \(\frac{x}{a}\)|\(\sqrt{1+\sinh ^{2} \frac{x}{a}}\)
= a. cosh \(\frac{x}{a}\). cosh \(\frac{x}{a}\) = a. cosh² \(\frac{x}{a}\)
Length of the sub normal = |y1 f'(x1)|

Question 4.
Find the lengths of subtangent, sub normal at a point t on the curve x = a (cos t + t sin t), y=a (sin t – t cos t)
Solution:
Equations of the curve are x = a (cos t + t sin t)
\(\frac{dx}{dt}\) = a (- sin t + sin t +1 cost) = at cos t
y = a (sin t – t cos t)
\(\frac{dy}{dt}\) = a (cos t – cos t +1 sin t) = a t sin t
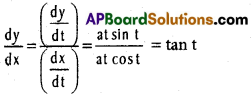
Length of the sub tangent
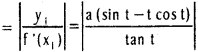
= |a cot t (sin t – t cos t)|
Length of the sub-normal = |y1.f'(x1)|
= |a (sin t – t cos t) tan t|
= |a tan t (sin t – t cos t)|