TS Inter 2nd Year Maths 2A Question Paper May 2019

Thoroughly analyzing TS Inter 2nd Year Maths 2A Model Papers and TS Inter 2nd Year Maths 2A Question Paper May 2019 helps students identify their strengths and weaknesses.

TS Inter 2nd Year Maths 2A Question Paper May 2019

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three Sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer all questions.
• Each question carries two marks.

Question 1.
Write the conjugate of the complex number \(\frac{5 i}{7+i}\).
Solution:

Question 2.
If z₁ = -1, z₂ = -i, then find Arg(z₁, z₂).
Solution:

Question 3.
If 1, w, w² are the cube roots of unity, then prove that (a + b)(aw + bw²)(aw² + bw) = a³ + b³.
Solution:
Since 1, w, w² are the cube roots of unity.
∴ 1 + w + w² = 0 and w³ = 1
L.H.S. = (a + b) (aw + bw²) (aw² + bw)
= (a + b) (a²w³ + abw² + abw⁴ + b²w³)
= (a + b) [a² . 1 + ab(w² + w³ . w) + b² . 1]
= (a + b) [a² + ab(w² + w) + b²]
= (a + b) (a² + ab(-1) + b²]
= (a + b) (a² – ab + b²)
= a³ – b³
= R.H.S.
∴ (a + b) (aw + bw²) (aw² + bw) = a³ – b³

Question 4.
If α, β are the roots of ax² + bx + c = 0, then find the value of α² + β² in terms of a, b, c.
Solution:
Since α, β are the roots of ax² + bx + c = 0
∴ α + β = \(\frac{-b}{a}\) and αβ = \(\frac{c}{a}\)
α² + β² = (α + β)² – 2αβ
= \(\left(\frac{-b}{a}\right)^2-2\left(\frac{c}{a}\right)\)
= \(\frac{b^2}{a^2}-\frac{2 c}{a}\)
= \(\frac{b^2-2 a c}{a^2}\)

Question 5.
If the product of roots of 4x³ + 16x² – 9x – a = 0 is 9, then find a.
Solution:
Given the product of roots of 4x³ + 16x² – 9x – a = 0 is 9
⇒ \(\frac{-(-a)}{4}\) = 9
⇒ \(\frac{a}{4}\) = 9
⇒ a = 36

Question 6.
Find the number of ways of arranging the letters of the word SINGING, so that they begin and end with I.
Solution:
The word SINGING contains 2I’s, 2N’s, and 2G’s.
For the required arrangement, first, we fill the first and last places with I in \(\frac{2 !}{2 !}\) = 1 way

The remaining 5 places can be filled with the remaining 5 letters, it can be done in \(\frac{5 !}{2 ! 2 !}\) ways.
∴ The number of required arrangements = 30

Question 7.
If ¹²C_r+1 = ¹²C_3r-5, then find r.
Solution:
Given ¹²C_r+1 = ¹²C_3r-5
⇒ r + 1 = 3r – 5 (or) 12 = r + 1 + 3r – 5
⇒ 1 + 5 = 3r – r (or) 12 = 4r – 4
⇒ 6 = 2r (or) 16 = 4r
⇒ r = 3 (or) 4

Question 8.
Find the set of values of x for which the binomial expansion of \((3-4 x)^{3 / 4}\) is valid.
Solution:

Question 9.
Find the mean deviation from the mean for the following discrete data:
6, 7, 10, 12, 13, 4, 12, 16
Solution:
Given data 6, 7, 10, 12, 13, 4, 12, 16
Mean = \(\frac{6+7+10+12+13+4+12+16}{8}\)
= \(\frac{80}{8}\)
= 10
Absolute values about the mean are |6 – 10|, |7 – 10|, |10 – 10|, |12 – 10|, |13 – 10|, |4 – 10|, |12 – 10|, |16 – 10| = 4, 3, 0, 2, 3, 6, 2, 6
∴ Mean deviation from mean = \(\frac{4+3+0+2+3+6+2+6}{8}\)
= \(\frac{26}{8}\)
= 3.25

Question 10.
8 coins are tossed simultaneously. Find the probability of getting 6 heads.
Solution:
Let A be the event getting 6 heads when 8 coins are tossed and ‘S’ be the sample space.
∴ n(S) = 2⁸ = 256
n(A) = ⁸C₆
= ⁸C₂
= \(\frac{8.7}{2}\)
= 28
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{28}{256}=\frac{7}{64}\)

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Attempt any five questions.
• Each question carries four marks.

Question 11.
If x + iy = \(\frac{3}{2+\cos \theta+i \sin \theta}\), then show that x² + y² = 4x – 3.
Solution:

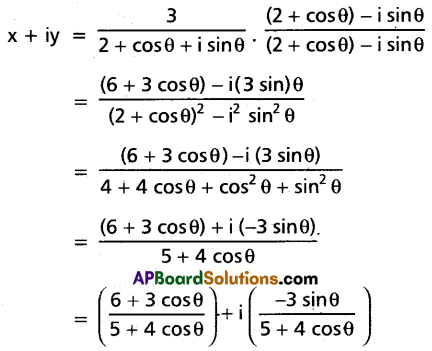
Question 12.
If x ∈ R, then determine the range of the expression \(\frac{x+2}{2 x^2+3 x+6}\).
Solution:
Let y = \(\frac{x+2}{2 x^2+3 x+6}\)
⇒ x + 2 = 2yx² + 3xy + 6y
⇒ 2yx² + (3y – 1)x + (6y – 2) = 0
x ∈ R ⇒ (3y – 1)² – 4(2y)(6y – 2) ≥ 0
⇒ 9y² – 6y + 1 – 48y² + 16y ≥ 0
⇒ -39y² + 10y + 1 ≥ 0
⇒ 39y² – 10y – 1 ≤ 0
⇒ 39y² – 13y + 3y – 1 ≤ 0
⇒ 13y(3y – 1) + (3y – 1) ≤ 0
⇒ (13y + 1)(3y – 1) ≤ 0
⇒ y ∈ \(\left[\frac{-1}{13}, \frac{1}{3}\right]\)
∴ Range of \(\frac{x+2}{2 x^2+3 x+6}\) is \(\left[\frac{-1}{13}, \frac{1}{3}\right]\)

Question 13.
If the letters of the word MASTER are permuted in all possible ways and the words thus formed are arranged in the dictionary order, then find the rank of the word REMAST.
Solution:
The Alphabetical order of the letters of the word MASTER is A, E, M, R, S, T.
The number of words that begin with
A – – – – – = 5! = 120
E – – – – – = 5! = 120
M – – – – – = 5! = 120
R A – – – – = 4! = 24
R E A – – – = 3! = 6
The next word is REMAST = 1
∴ Rank of the word REMAST is = 120 + 120 + 120 + 24 + 6 + 1 = 391

Question 14.
Find the number of ways of forming a committee of 5 members out of 6 Indians and 5 Americans, so that always the Indians will be in the majority in the committee.
Solution:
Since the committee always contains the Indians majority.
∴ The members of the committee may be of the following three types.

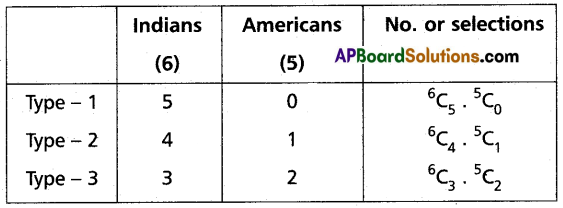
∴ The required number of ways of selecting the committee = ⁶C₅ × ⁵C₀ + ⁶C₄ × ⁵C₁ + ⁶C₃ × ⁵C₂
= 6 × 1 + 15 × 5 + 20 × 10
= 6 + 75 + 200
= 281 ways

Question 15.
Resolve \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}\) into partial fractions.
Solution:
Let \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+2}\)
⇒ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A\left(x^2+2\right)+(B x+C)(x-1)}{(x-1)\left(x^2+2\right)}\)
⇒ 2x² + 3x + 4 = A(x² + 2) + (Bx + C) (x – 1) ………(1)
Put x = 1
2 + 3 + 4 = A(1 + 2)
⇒ 9 = 3A
⇒ A = 3
Comparing the coefficient of x2 terms on both sides in (1)
2 = A + B
⇒ 2 = 3 + B
⇒ B = -1
Comparing constant terms on both sides in (1)
4 = 2A – C
⇒ C = 2A – 4
⇒ C = 2(3) – 4
⇒ C = 2
∴ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{-x+2}{x^2+2}\)
∴ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{2-x}{x^2+2}\)

Question 16.
Find the probability of drawing an ace or a spade from a well-shuffled pack of 52 playing cards.
Solution:
Let A be the event of getting an ace card B be the event of getting a spade card from a shuffled pack of 52 cards and S be the sample space.
n(S) = ⁵²C₁ = 52
n(A) = ⁴C₁ = 4
n(B) = ¹³C₁ = 13
n(A ∩ B) = ¹C₁ = 1
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{4}{52}\)
P(B) = \(\frac{n(B)}{n(S)}=\frac{13}{52}\)
P(A ∩ B) = \(\frac{n(A \cap B)}{n(S)}=\frac{1}{52}\)
∴ P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{4}{52}+\frac{13}{52}-\frac{1}{52}\)
= \(\frac{16}{52}\)
= \(\frac{4}{13}\)

Question 17.
If A and B are two events with P(A ∪ B) = 0.65, P(A ∩ B) = 0.15, then find the value of P(AC) + P(BC).
Solution:
Given P(A ∪ B) = 0.65, P(A ∩ B) = 0.15
P(AC) + P(BC) = 1 – P(A) + 1 – P(B)
= 2 – [P(A) + P(B)]
= 2 – [P(A ∪ B) + P(A ∩ B)]
= 2 – [0.65 + 0.15]
= 2 – 0.80
= 1.2
∴ P(AC) + P(BC) = 1.2

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Attempt any five questions.
• Each question carries seven marks.

Question 18.
If n is a positive integer, then show that (1 + i)ⁿ + (1 – i)ⁿ = \(2^{\frac{n+2}{2}} \cos \left(\frac{n \pi}{4}\right)\).
Solution:

Question 19.
Find the algebraic equation whose roots are the translations of the roots of the equation x⁴ – 5x³ + 7x² – 17x + 11 = 0 by -2.
Solution:
Let f(x) = x⁴ – 5x³ + 7x² – 17x + 11
The algebraic equation whose roots are the translates of the roots of the equation f(x) = 0 by -2 is f(x + 2) = 0
⇒ (x + 2)⁴ – 5(x + 2)³ + 7(x + 2)² – 17x + 11 = 0
⇒ x⁴ + 4 × x³ × 2 + 6 × x² × 4 + 4 × x × 8 + 16 – 5(x³ + 3 × x² × 2 + 3 × x × 4 + 8) + 7(x² + 4x + 4) – 17(x + 2) + 11 = 0
⇒ x⁴ + 8x³ + 24x² + 32x + 16 – 5x³ – 30x² – 60x – 40 + 7x² + 28x + 28 – 17x – 34 + 11 = 0
⇒ x⁴ + 3x³ + x² – 17x – 19 = 0

Question 20.
For r = 0, 1, 2,…….. n, prove that C₀ C_r + C_r C_r+1 + C₂ C_r+2 + …….. + C_n-r C_n = ²ⁿC_n+r and hence deduce that \(C_0^2+C_1^2+C_2^2+\ldots \ldots+C_n^2={ }^{2 n} C_n\).
Solution:

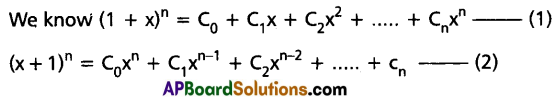
Question 21.
Find the sum of infinite series \(\frac{3}{4.8}-\frac{3.5}{4.8 .12}+\frac{3.5 .7}{4.8 \cdot 12.16}\) – ……….
Solution:

Question 22.
Calculate the variance and standard deviation for the discrete frequency distribution given below:

xi	4	8	11	17	20	24	32
fi	3	5	9	5	4	3	1

Solution:
Construct the following table.

Question 23.
A fair die is rolled. Consider the events A = {1, 3, 5} B = {2, 3} and C = { 2, 3, 4, 5} find:
(i) P = (A ∪ B)
(ii) P(A/B)
(iii) P = (A/C)
(iv) P = (B/C)
Solution:
Given A = {1, 3, 5}, B = {2, 3} and C = { 2, 3, 4, 5}
A fair die is rolled.
∴ S = {1, 2, 3, 4, 5, 6}
⇒ n(S) = 6
∴ P(A) = \(\frac{3}{6}=\frac{1}{2}\)
P(B) = \(\frac{2}{6}=\frac{1}{3}\)
P(C) = \(\frac{4}{6}=\frac{2}{3}\)

(i) A ∪ B = {1, 2, 3, 5}
⇒ n(A ∪ B) = 4
∴ P(A ∪ B) = \(\frac{n(A \cup B)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)

(ii) A ∩ B = {3}
⇒ n(A ∩ B) = 1
P(A ∩ B) = \(\frac{1}{6}\)
\(P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}\)
= \(\frac{\frac{1}{6}}{\frac{2}{6}}\)
= \(\frac{1}{2}\)

(iii) A ∩ C = {3, 5}
⇒ n(A ∩ C) = 2
P(A ∩ C) = \(\frac{2}{6}\)
\(p\left(\frac{A}{C}\right)=\frac{p(A \cap C)}{p(C)}=\frac{\frac{2}{6}}{\frac{4}{6}}=\frac{2}{4}=\frac{1}{2}\)

(iv) B ∩ C = {2, 3}
⇒ n(B ∩ C) = 2
P(B ∩ C) = \(\frac{2}{6}\)
\(p\left(\frac{B}{C}\right)=\frac{p(B \cap C)}{p(C)}=\frac{\frac{2}{6}}{\frac{4}{6}}=\frac{2}{4}=\frac{1}{2}\)

Question 24.
The probability distribution of a random variable X is given below.

X = xi	1	2	3	4	5
P(X = xi)	k	2k	3k	4k	5k

Find the value of k and the mean and variance of X.
Solution:
We have \(\sum_{i=1}^5 P\left(X=x_i\right)\) = 1
⇒ k + 2k + 3k + 4k + 5k = 1
⇒ 15k = 1
⇒ k = \(\frac{1}{15}\)
Mean µ of x = \(\sum_{r=1}^5 r \cdot p\left(X=x_1\right)\)
= \(\sum_{r=1}^5 r(r k)\)
= 1(k) + 2(2k) + 3(3k) + 4(4k) + 5(5k)
= 55k
= 55 × \(\frac{1}{15}\)
= \(\frac{11}{3}\)
Variance (σ²) = (1)2 k + (2)2 2k + (3)2 3k + (4)2 4k + (5)2 (5k) – µ²
= k + 8k + 27k + 64k + 125k – \(\left(\frac{11}{3}\right)^2\)
= 225k – \(\frac{121}{9}\)
= 225 × \(\frac{1}{15}-\frac{121}{9}\)
= \(\frac{135-121}{9}\)
= \(\frac{14}{9}\)