Access to a variety of TS Inter 2nd Year Telugu Model Papers Set 5 allows students to familiarize themselves with different question patterns.
TS Inter 2nd Year Telugu Model Paper Set 5 with Solutions
Time : 3 Hours
Max. Marks : 100
సూచనలు :
- ప్రశ్నపత్రం ప్రకారం వరుసక్రమంలో సమాధానాలు రాయాలి.
- ఒక్క మార్కు ప్రశ్నల జవాబులను కేటాయించిన ప్రశ్న క్రింద వరుస క్రమంలో రాయాలి.
I. కింది పద్యాలలో ఒక పద్యానికి ప్రతిపదార్థ తాత్పర్యాలను రాయండి. (1 × 8 = 8)
1. భాగ్యనగరాత్యంత పరిసరమ్ముల బుట్టి
పాలమూ ర్మండలపు భాగాన బంధింప
బడి నీలగిరిసీమ బరగు దేవరకొండ
భూముల బండించి ముందు కటునటు సాగి
పలనాటి బ్రహ్మయ్య పరగణాలో బారు
కృష్ణమ్మలో గలసి కెలకుల నడయాడి
ఏలేశ్వరుని పూజ కేగి భక్తులతోడ
అట నుపాధ్యాయు కీర్త్యంశములు గొన్నింటి
వెలువరచి చరిత కొక వెలుగుబాటను జూపి
జవాబు:
ప్రతిపదార్థం :
భాగ్యనగర = హైదరాబాదుకు
అత్యంత పరిసరమ్ములన్ = అతి సమీపములో
పుట్టి = జన్మించి
పాలమూరు మండలపు = పాలమూరు (మహబూబ్నగర్) జిల్లా ప్రాంతంలో ఆనకట్టచే నిలుపబడి
భాగాన
బంధింపబడి = ఆనకట్టచే నిలుపబడి
నీలగిరిసీమన్ + పరగు = నీలగిరి (నల్లగొండ జిల్లా) ప్రాంతంలో ఉన్న
దేవరకొండ = దేవరకొండ
భూములన్ పండించి = పొలాలను పండే విధంగా చేసి
ముందుకు = ఇంకా ముందుకు
అటునటు = అలా అలా
సాగి = ప్రవహించి
పలనాటి బ్రహ్మయ్య = పలనాటి బ్రహ్మనాయుడు
పరగణాలో = పాలించిన ప్రాంతంలో
పారు = పారి
కృష్ణమ్మలో గలసి = కృష్ణానదిలో
కెలకుల = దగ్గరలో
నడయాడి = ప్రవహించి
ఏలేశ్వరుని పూజకు ఏగి = ఏలేశ్వర స్వామి పూజకు పోయి
భక్తుల తోడ = భక్తులతో
అటన్ = అక్కడ
ఉపాధ్యాయున్ = నాగార్జునుని
కీర్తి + అంశములన్ = కీర్తికి సంబంధించిన అంశాలను
కొన్నింటి = కొన్నిటిని
వెలువరచి = చెప్పి
చరితకు ఒక = చరిత్ర రాయడానికి ఒక
వెలుగుబాటను = కాంతి మార్గాన్ని
చూపి = చూపించి
తాత్పర్యం : హైదరాబాదుకు అతి సమీపంలో జన్మించి, మహబూబ్ నగర్ జిల్లాలో ఆనకట్టచే బంధించబడి, నల్లగొండ జిల్లాలోని దేవరకొండ ప్రాంతంలోని భూములలో పంటలు పండించి,
ఇంకా ముందుకు అలాఅలా ప్రవహించి, పలనాటి బ్రహ్మనాయుడు పాలించిన ప్రాంతంలో పారి కృష్ణానదికి అతి దగ్గరలో ఏలేశ్వర స్వామి పూజలు చేసి అక్కడి భక్తులకు ఆచార్య నాగార్జునుని కీర్తిని చెప్పి చరిత్ర రాయడానికి వెలుగు బాటలు చూపి.
2. కోకిలా! నాకు తెలుసు
ఎవరో సన్మానించాలన్న ఆశ నీకులేదు;
పై రవి మార్గం తప్ప –
‘పైరవి’ మార్గం నీకు తెలియదు
దైవమిచ్చిన కళను గళంవిప్పి ప్రదర్శిస్తున్నావు !
జవాబు:
ప్రతిపదార్థం:
కోకిలా! = ఓ కోకిలా
ఎవరో సన్మానించాలన్న = ఎవరో వచ్చి సన్మానాలు చేయాలనే
ఆశ నీకులేదు = కోరిక నీకు లేదని
నాకు తెలుసు = నాకు బాగా తెలుసు
పై రవి మార్గం తప్ప = పైన ఉన్న సూర్యుడు చూపిన మార్గం తప్ప
‘పైరవి’ మార్గం = పైరవీలు చేసే దారి
నీకు తెలియదు = నీకు తెలియదు.
దైవమిచ్చిన కళను = దేవుడు ప్రసాదించిన కళను
గళంవిప్పి ప్రదర్శిస్తున్నావు! = నీ గొంతు విప్పి ప్రదర్శిస్తున్నావు.
తాత్పర్యం : ఓ కోకిలా ఎవరో వచ్చి సన్మానాలు చేయాలనే కోరిక నీకు లేదనే విషయం నాకు తెలుసు. నీకు పైన ఉన్న సూర్యుడు చూపిన మార్గం మాత్రమె తెలుసు కాని పైరవీలు చేసి సన్మానాలు పొందే దారి తెలియదు అని కవి అన్నాడు. అంటే కొంతమంది కళాకారులు పైరవీల ద్వారా గుర్తింపును పొందుతున్నారని ఆ గుర్తింపు కోసమే ప్రదర్శనలు చేస్తారని చెప్తున్నాడు. కోకిల అలా కాకుండా తనకు దేవుడు ఇచ్చిన కళను నిస్వార్థంగా ప్రదర్శిస్తుందని
తెలిపాడు.

II. కింది వాటిలో ఒక ప్రశ్నకు 20 పంక్తులలో సమాధానం రాయండి. (1 × 6 = 6)
ప్రశ్న 1.
‘గంగా ప్రవాహం’ ఎలా కొనసాగిందో తెలుపండి.
జవాబు:
భగీరథుడు ఘోరమైన తపస్సు చేసి బ్రహ్మను, శివున్ని ప్రసన్నం చేసుకున్నాడు. గంగను తన తలపై భరిస్తానని శివుడు ఇచ్చిన మాట గంగకు కోపం తెప్పించింది. తన ప్రవాహ వేగంతో శివున్ని పాతాళానికి తొక్కి వేస్తానని గంగ భావించింది. గంగ గర్వాన్ని తొలగించాలని శివుడు అనుకున్నాడు.
ఆ సమయంలో దేవలోకంలో ప్రవహించే గంగానది సహింపరాని వేగంతో, గెలవాలనే కోరికతో, పెద్ద శబ్దంచేస్తూ, మూడులోకాలకు భయాన్ని కలిగించే విధంగా మ్రోగుతూ హిమాలయ పర్వతంలాగా ప్రకాశిస్తున్న శివుని తలపై పడింది.
ఈ విధంగా శివుని తలపై పడి శివుని జడలనే అడవిలో ఎన్నో సంవత్సరాలు మబ్బులలో కదులుతున్న మెరుపులాగా తిరుగుతూ ఉంది. దేవతలందరూ శంకరుని వద్దకు వచ్చి, నమస్కరించి, కీర్తించి మూడు లోకాలకు పాలకుడా! నీ గొప్ప మహిమ తెలియక దేవనది అయిన గంగ ప్రదర్శించిన గర్వము నీ మాయచేత నశించింది. నిజభక్తుడైన భగీరథునిపై గల కరుణతో అయినా దేవనదిని
విడుదల చేయవలెను. తమరు అనుగ్రహిస్తే ఈ గంగా జలముతో సగరపుత్రుల ప్రేతాత్మలు శాంతిని పొందుతాయి. మానవ లోకానికి, పాతాళ లోకానికి గొప్ప మేలు కలుగుతుంది అని దేవతలు వేడుకొనగా పరమశివుడు గంగానదిని సముద్రంలోకి వదిలాడు. శివుని జడలనుండి విడువబడిన గంగానది భాసురహ్లాదినీ, పావనీ, నందినీ, సీతా, సుచక్షు, సింధు, అనే ఆరుపాయలు తూర్పు, పడమరలకు వెళ్ళాయి.
ఏడవదైన ఒక ప్రవాహం ఎంతో అందంగా ఆ భగీరథుని వద్దకు బయలుదేరింది. అలా గంగానది తనవెంట రావడం గమనించిన భగీరథుడు గొప్ప రథంపై ఎక్కి పాతాళానికి కదిలాడు.
అనేక ప్రదేశాలలో నివసించే ప్రజలు ఆనందం ఉట్టిపడగా దేవనదీ జలాలలో సంతోషంగా స్నానాలు చేశారు. వారంతా భయాన్ని కలిగించే ప్రేత స్వభావాన్ని వదిలి శాశ్వతమైన వైభవాన్ని కలిగించే స్వర్గానికి చేరుకున్నారు. శివుని శరీరాన్ని తాకినందున మరింత పవిత్రంగా మారిన దేవనది జలములు అనుకుంటూ ఇంద్రుడు మొదలైన దేవతలు, యక్షులు, గంధర్వులు, మునుల సమూహాలు వారి కోరికలు తీరేలాగా అనేక సార్లు ఆనదిలో స్నానం చేశారు.
జహ్నువు అనే మహారాజు యజ్ఞం చేస్తుండగా గంగానది అతని యాగశాలను ముంచి వేసింది. దానికి కోపించిన జహ్నువు సముద్రాన్ని మింగిన అగస్త్యుని లాగా ఆనదిని మింగినాడు. దేవతలందరూ ఆశ్చర్యచకితులై రాజర్షులలో శ్రేష్ఠుడైన జహ్నువుతో ఓ మహానుభావా నీ తపస్సు అద్భుతము. నీ మహిమతో సముద్రాన్ని తాగిన అగస్త్యున్ని మరిపింప చేశావు. గంగాదేవి పొగరు (గర్వం) అణిగింది.
ఇకపై ఈ భూమిపై గంగ నీకూతురుగా గుర్తించబడుతుంది. కావున నీవు గంగను విడువవలెను అని అనగానే జహ్నుమహర్షి దేవతలందరూ ఆశ్చర్యపడగా తన చెవుల నుండి గంగను వదిలిపెట్టాడు. గంగ భగీరథుని రథం వెంబడి సముద్రం వైపు వెళ్ళింది.
ఎండిపోయిన సముద్రంలో, సాగరులు తవ్విన రంధ్రం ద్వారా, భగీరథుని వెంట పాతాళానికి వెళ్ళి, సగరపుత్రుల బూడిదకుప్పలు తడిసేవిధంగా ప్రవహించింది. దానితో సాగరులకు పాపములు పోయి దివ్యరూపాలు వచ్చాయి. వారు దేవతలలాగా విమానాలలో పట్టరాని ఆనందంతో భగీరథుడు చూస్తుండగా గొప్పదైన స్వర్ణాన్ని అధిరోహించారు. అప్పటి నుండి గంగానది జహ్ను మహర్షి కూతురు కాబట్టి జాహ్నవి అని, భగీరథుని కూతురు కాబట్టి భాగీరథి అనే పేర్లతో ఈ భూమిపై ప్రవహిస్తుంది.
ప్రశ్న 2.
సిద్ధప్ప జ్ఞానబోధలోని నీతులు వివరించండి.
జవాబు:
నాయనలారా! వినండి. మీ హితాన్ని కోరే ఈ సిద్ధప్ప చెప్పిన కవిత్వం బంగారపు కుప్పవంటిది జాగ్రత్తగా గమనించండని చెప్తూ వరకవి సిద్ధప్ప తన జ్ఞానబోధలో నీతులను వివరించాడు. కుమ్మరి చేసే కుండల్లో కొన్ని చేస్తున్నప్పుడు, కొన్ని సారెమీద, కొన్ని తెలియకుండానే పగిలిపోతాయి. కొన్ని ఆవములో పగలగా కొన్ని మాత్రమే మంచిగా తయారై కొన్ని రోజులు ఉపయోగపడిన తరువాత పగిలిపోతాయి.
అలాగే మానవులు కూడా మర్యాదతో ప్రవర్తిస్తేనే ఈ భూమిపై మోక్షాన్ని పొందుతారు. కోపంతో మానవత్వం పోతుంది. కోపం నష్టపరుస్తుంది, పాపం పెరిగేలా చేస్తుంది. కోపం వల్ల నిందలు వస్తాయి. కోపం ఎలా పోతుందో ఎవరికీ తెలియదు. కోపం స్నేహితులను అవమానపరుస్తుంది.
కోపంతో శాపాలు వస్తాయి. చూస్తుండగానే కొరివిగా మారి మానవులను నాశనం చేస్తుంది. కాబట్టి కోపానికి దూరం ఉండాలని చెప్పాడు.
డబ్బు ఉన్నవారిని గౌరవిస్తారు. కాని పేదవారి గుర్తించరు. సమయం ఎప్పటికీ ఒకే విధంగా గడవదు. నేనే బలవంతుణ్ణి అని గర్వించడం సరికాదు. చలిచీమలు కూడా పామును చంపుతాయి. కాబట్టి ఎదుటి వారి ముందు గొప్పలు చెప్పుకోవద్దు. కుండవంటి ఈ శరీరాన్ని నమ్మరాదు.
తొమ్మిది రంధ్రాలున్న ఇల్లు ఇది. బతుకమ్మలాగా ఎప్పుడైనా నీటిలో ప్రవేశించవచ్చు. చనిపోయిన తరువాత తల్లి, తండ్రి, బంధువులు ఎవరూ తిరిగి చూడరు. మరిచిపోతారు. కాటికి వెళ్ళేటపుడు ఒక్క కాసుకూడా వెంటరాదు. సంసారం అంతా అబద్ధం అని తెలియక పప్పు తినడానికి వెళ్ళిన ఎలుక లాగ అనేక రకాలుగా డబ్బును సంపాదిస్తుంది. ఆస్తులు, కులం, అధికారం, సంసారం ఇలా అనేక విషయాలపై మోహంతో భక్తి లేక ఉన్నతమైన మానవ జన్మ ఎత్తి కూడా చేప గాలాన్ని మింగినట్లు మనుషులు సంసారమనే మాయలో పడి యమధర్మరాజు చేతికి చిక్కి బాధపడతారు.
వేదాలు తెలిసిన వేమన తాతలాంటి వాడు. సురలను ఆనందింపచేసే సుమతి శతక కర్త బద్దెన పెద్దమ్మ వంటి వాడు. కాలజ్ఞానాన్ని రాసిన పోతులూరి వీరబ్రహ్మం తండ్రి లాంటి వారు. ఈశ్వరమ్మ అక్క లాంటిది. సిద్ధప్ప అన్న వంటి వాడు. కాళిదాసు మా చిన్నన్న. అమరసింహుడు, యాగంటి ఆత్మ బంధువుల వంటి వారు. వీరంతా చనిపోయికూడా జనాల హృదయాలలో బతికే ఉన్నారు. వారిలాగా లోక కళ్యాణం కోసం జీవించాలి.
నాలుక తండ్రి పరమాత్మ వంటిది. కళ్ళు అల్లుళ్ల వంటివి, రెండు చేతులు ఆత్మ బంధువుల వంటివి. కడుపు పెద్ద నాన్న కొడుకు, చూసే రెండు కళ్ళు మేనమామలు, వినే రెండు చెవులు అన్నదమ్ములు, ముక్కు ప్రియురాలు, ముఖం మేనత్త, దంతాలు చుట్టాలు, భక్తులు. నాలుక ఆదిపరాశక్తి అయిన మా ఇంటి దేవత. జ్ఞానేంద్రియాలు, కర్మేంద్రియాలు మానవ జీవనానికి అత్యంత ప్రధానమైనవి వాటిని పవిత్రంగా, జాగ్రత్తగా చూసుకోవాలని చెప్పాడు.
చేదుగా ఉన్న ఆనగపు కాయను చేతిలో పట్టుకొని గంగానదిలో స్నానం చేసి దాని రుచిచూస్తే అంతకు ముందు ఉన్న చేదు రుచి పోదు. లేని తీపి రుచి రాదు. ఆ సొరకాయలాగా మానవులు కూడా గంగలో మునిగి తేలితే వారి మూర్ఖత్వం పోదు. ఎన్ని నదుల దగ్గరికి వెళ్ళినా, ఎన్ని వ్రతాలు పట్టినా పాపాత్ములు మోక్ష పదవిని అలంకరించలేరు. వంకరగా ఉన్న కుక్క తోకకు వెదురు కర్రలు ఎంత లాగి కట్టినా దాని వంకర గుణం పోదు. గురువును మనస్సులో నిలిపితే పైన చెప్పిన అసాధ్యమైన పనులు చేసి ప్రతిష్ఠ పొందవచ్చు.
ఎవరైతే తన ఆత్మను పరమాత్మతో సమానంగా భావించి, అన్ని జీవులను సమానంగా చూసి జ్ఞాన వైరాగ్యాలనే యజ్ఞాన్ని, దానాలను, తపస్సులను చేస్తారో వారు మోక్షాన్ని పొందుతారు. తామరాకులు నీటిలో ఉండి కూడా తడవకుండా ఉన్నట్లుగానే భూమిపై జీవిస్తున్న జ్ఞానులు కూడా అలసిపోయినట్లు, కళా విహీనంగా కనిపిస్తారు. కాని తరువాత వారి ముఖంలో కళ వస్తుందని సిద్ధప్ప నీతులను చెప్పాడు.
III. కింది వాటిలో ఒక ప్రశ్నకు 20 పంక్తులలో సమాధానం రాయండి. (1 × 6 = 6)
ప్రశ్న 1.
పాఠ్యాంశం ఆధారంగా చిందు భాగోతం ప్రదర్శన గురించి తెలుపండి.
జవాబు:
చిందు భాగవతం ప్రదర్శించడానికి ముందు నాలుగు గుంజలు, వెనక రెండు గుంజలు పాతి పందిరి వేస్తారు. ఆ పందిరి కిందనే భాగోతం ప్రదర్శిస్తారు. పందిరి లేకుంటే భాగోతం ఆడరు. పందిరిని చాందిని అని కూడా అంటారు. పందిరికి మూడుపక్కల . ఎడ్లకు కట్టే పగ్గాల కంటే లావుగా ఉండే జనుముతో చేసిన తాళ్లను కట్టేవారు. భాగోతం చూడడానికి వచ్చిన వారు మీద పడకుండా ఈ తాళ్ళను కట్టేవారు.
దొమ్మరి బిడ్డ గడ (రెండువైపులా కర్రలు పాతి వాటి మధ్యలో తాడు కట్టేవారు. ఆ తాడుపై పెద్ద కర్ర పట్టుకొని నడిచేవారు) ఎక్కి, సాలా పులిగోలిగా అని బియ్యం సల్తది. మాదిగ చిందోల్లు ఎల్లమ్మ యేషం గట్టి చెరువుల మొకం కడిగితేనే మోక్షం, బరుకతు అని భావించే వారు. అట్లాంటిది మారిపోయి నడి ఊర్లో భాగోతం ఆడటం ఎల్లమ్మ తాతల కాలంలోనే ప్రారంభమైంది.
“ఇవ్వాల చిందు భాగోతం ఆడుతుండ్రట, పోవాలరా” అనేవారు. ఇవ్వాల “ఎల్లమ్మ ఆట ఆడుతున్నరు. గావు పట్టేదున్నదట పోవాల” అని ఊరివాల్లు వచ్చేవారు. పాత రోజుల్లో రాత్రులు ఊర్లో భాగోతం ఆడుతున్నపుడు మంగలోలు దివిటీలు పట్టేవారు.
వేషాలు తయారు అయేటపుడు ఎవరూ చూడకుండా జాగ్రత్తపడేవారు. తెరముందు ఆడేటప్పుడు మాత్రమే అందరూ చూడాలి అనుకునేవారు. అందుకోసం మాదిగ ఇండ్లల్లో వేషం ధరించేవారు. అలా కుదరనప్పుడు పందిరికి కొంత దూరంలోనో, అలాకూడా కుదరనప్పుడు చుట్టూ దుప్పటి కట్టుకొని రంగులు వేసుకునే వారు. రంగులు వేసుకున్నాక దుప్పటి కప్పుకొని భాగోతం ప్రదర్శించే పందిరి లోపలికి వచ్చేవారు. కళాకారులు ఎవరి వేషం (మేకప్) వాల్లే వేసుకునే వారు. ఎవరి అద్దం వాల్లదగ్గరే ఉండేది.
మొకంకు రేవిడిని, లేకుంటే పసుపు పచ్చ పౌడరును వేసుకునే వారు. తెల్ల వెంట్రుకలు కావాలంటే మెంచు, లేదా అర్దూలం (జింక్ ఆక్సైడ్) వాడేవారు. ఆ అర్దూలం చెమటకు వెంటనే కరిగిపోయేది, చూసేవారు కంటికి ధారలుపడేటట్టు ఏడుస్తున్నారు అనుకునే వాళ్ళు.
పాత రోజుల్లో ఏడుపు రావాలంటే కంట్లో వేలు పెట్టుకోవడం లేదా నూనె చుక్కలు వేసుకునేవారు. కాని ఎల్లమ్మకు దుఃఖం పాట పాడగానే ఏడుపు వచ్చేది. భాగోతం చూసేవారు కూడా వెక్కివెక్కి ఏడ్చేవారు. వారు ఏడిస్తే చీరకొంగులు తడిసిపోయేవి.
అంత కష్టపడి భాగోతాన్ని రసవంతంగా ప్రదర్శించేవారు. సత్యహరిశ్చంద్ర భాగోతం ఆడితే చూసేవారు కూడా ఏడ్చేవారు. అలా ప్రదర్శిస్తున్నప్పుడు ఒక్కోసారి ఆఊరి దొరలు “మేం ఇట్లనే కొంగులు పెట్టుకొని ఏడుద్దుమా? బంజేస్తరా? ఓ గంగారం!, ఓ ఎల్లవ్వా! ఇదేం ఏడుసుడు. ఏం కథ, దేవుడా… జర బందు జేయుండ్రి గదా!” అని చెప్పేవారు. అంత లీనమై ఆ ప్రదర్శనను చూసేలా ఆడేవారు.
అంత కష్టపడి ప్రదర్శిస్తేనే ఆ కళకు అంతర్జాతీయ స్థాయిలో గుర్తింపు వచ్చింది. ఇప్పుడు భాగోతం ఉదయం పదకొండు గంటలకు ప్రారంభిస్తే సాయంత్రం ఆరు, యేడు గంటల దాకా ఆడతారు. ఈ భుజకీర్తులు, కిరీటాలను అంతసేపు అట్లనే ధరించాలి. వేషాల మధ్య తబలకొట్టినా కూడా వాటిని అలానే ధరించేవారు. భాగోతం పూర్తయి ఇంటికి వచ్చి, ఆరతి ఇచ్చిన తరువాతనే వేషాన్ని విప్పేవారు.
ప్రదర్శన ప్రారంభ ముగింపు సన్నివేశాలు: ఏదైనా గ్రామంలో ప్రదర్శన ప్రారంభించే ముందు ఆవూర్లోని విశ్వబ్రాహ్మణుల ఇంటికి వెళ్లి వారి కొలిమికి నమస్కరించేవారు. భాగోతం ఆడటం అయిపోయినంక రాముని పేరుతో మంగళహారతి ఇస్తారు. పక్కవాయిద్యాల వారు కూడా మంగళారతి పాట పాడేవారు.
ప్రధాన వేషం ధరించిన స్త్రీ పాత్ర మంగళహారతి పట్టుకొని ప్రేక్షకుల దగ్గరికి పొతే, వారు ఆ హారతికి నమస్కరించి వారికి తోచినంత డబ్బును హారతి పళ్ళెంలో వేసేవారు. ఆ తరువాత ఆ హారతితోనే కళాకారుల బృందం అంతా ఇంటికి వెళ్తారు. అందరు కలిసి మరొక్కసారి హారతి తీసుకుంటారు.
హారతి ఒకరినొకరిని హృదయాలకు హత్తుకుని ఆడవారితో ఆడవారు, మగవారితో మగవారు దాసున్ని అనే అర్థంలో ‘దాసున్, దాసున్’ అనుకుంటారు. అప్పుడు భాగోతం సామాగ్రినంతా తీసి, ఎవరి సామాను వారు సర్దుకొని వేషాన్ని విప్పేస్తారు. ప్రదర్శనలో భాగంగా అరేయ్ దుర్మార్గా అని, ఓరి సుగ్రీవా అని పాడి, ఎగిరి తంతారు.
అలా చేయడం తప్పు కాబట్టి భాగోతం పూర్తికాగానే పెద్దవారి కాళ్లకు నమస్కరిస్తారు. అలా భాగోతంలో ‘అన్నా అనకున్నా, తన్నినా తన్నకున్నా, చిన్నవారు పెద్దలకు నమస్కరిస్తారు.

ప్రశ్న 2.
ప్రపంచంలో రాబోయే పరిణామాలను రచయిత ఏవిధంగా ఊహిస్తున్నాడు ?
జవాబు:
ది ఏజ్ ఆఫ్ ది స్పిరుట్యువల్ మెషిన్స్ అనే పుస్తకాన్ని రాసిన రే కురువైల్ చెప్పిన దాని ప్రకారం 2009 నాటికి 50,000 ఖరీదు చేయగల కంప్యూటరు ఒక్క సెకండులో కోటి లక్షల లెక్కలు చేయగలదు. 2019 నాటికి సెకండుకు 10 లక్షల కోట్ల లక్షల లెక్కలు చేయగలదు. అంటే అప్పటికి దాదాపుగా మానవ మేధకు సమానమైన సామర్థ్యాన్ని సాధించగలదు.
2029 నాటికి అది ఒక వెయ్యి మానవ మేధస్సులకు సమానమైన సామర్థ్యాన్ని పొందుతుంది. అంటే భవిష్యత్తులో మానవులు నేడు తాము చేసే పనులు కొన్నింటిని కంప్యూటర్లతో నడిచే రోబోక్స్కి అప్పజెప్పి తమ మెదడుల్ని మరింత ప్రయోజనకరమైన పనులకు అప్పజెప్పే అవకాశం ఉంటుంది. అప్పుడు వాళ్లు తమ భావనా సామర్థ్యంతో ప్రయోగశీల ఆలోచనతో తిరిగి మళ్లీ కంప్యూటర్లను ఓడించగలిగే స్థాయికి చేరుకుంటారు.
ఈ శతాబ్దం చివరికి మానవ ఆలోచనలను, యంత్రాల తెలివితేటలను విలీనం చేసే ధోరణి బలంగా పెరుగుతుంది. అప్పుడు మానవుడు ఒకప్పుడు రూపొందించిన యంత్రాలకూ, మానవ మేధాశక్తికీ మధ్య సరిహద్దులు చెరిగిపోతాయి. అటువంటి పరిస్థితిలో యంత్రాల బారినుండి మానవుడి ప్రత్యేకతను మనం ఏవిధంగా : నిలబెట్టుకోగలుగుతామో తెలియదు. నిస్సందేహంగా కంప్యూటర్లు ఒక సవాలుగా మారుతున్నాయి. ఈ సమస్య కేవలం జీవశాస్త్రవేత్తలదీ, జీవసాంకేతికవేత్తలదీ మాత్రమేకాదు.
మొత్తం శాస్త్రవేత్తలు అందరు మనుష్యులు రూపొందించిన కంప్యూటర్లకన్నా మానవ జాతిని ఒక మెట్టు పైనే ఉంచవలసిన గొప్ప బాధ్యత తలకెత్తుకోవలసి ఉంది. అదృష్టవశాత్తూ మానవ మేధ సృజనాత్మకత, ప్రయోగశీల పార్శ్వాలు ఎంత గొప్పవంటే అవి మనిషిని ఎన్నటికి యంత్రం ముందు ఓడిపోనివ్వవు.
మానవజాతిలో సహజసిద్ధమైన, అంతర్గతమైన మహాశక్తిని పరిపూర్ణంగా ఆవిష్కరించే దిశగా హ్యూమన్ జీనోమ్ సాఫ్ట్వేర్ను మనమింకా అభివృద్ధి చేయవలసి ఉంది. అని ప్రపంచంలో రాబోయే పరిణామాలను కలాం ఉహించాడు.
IV. కింది వాటిలో రెండు ప్రశ్నలకు 15 పంక్తులలో సమాధానం రాయండి. (2 × 4 = 8)
ప్రశ్న 1.
ముద్దు రామకృష్ణయ్య గారి ప్రథమ విదేశయాత్ర సన్నాహాలు వివరించండి.
జవాబు:
ముద్దు రామకృష్ణయ్య మొదటి ప్రయత్నం విఫలం అయ్యాక 1944 లో తన తోటి ఉపాధ్యాయుడు దిగంబరరావు తో మాట్లాడుతూ డబ్బు లేని కారణంగా ఇంగ్లాండు వెళ్లలేదని చెప్పాడు. ఆయన డిప్యూటి కలెక్టర్, పోలీసు సర్కిల్ ఇన్స్పెక్టర్ మీ మిత్రులే కదా వారు సహకరించరా అని సలహా ఇచ్చాడు.
మళ్ళీ విదేశాలకు వెళ్లాలని ప్రయత్నాలు ప్రారంభించి థామస్ కుక్ వారికి ఇంగ్లాండ్ వెళ్ళడానికి పడవ ఉందా అని లేఖ రాశాడు. సెప్టెంబర్ లో పడవ బయలుదేరుతుందని, బ్రిటీష్ రెసిడెన్సి నుండి పాస్పోర్ట్ తీసుకొమ్మని, సీటు రిజర్వు చేసినట్టు వారు జవాబు పంపారు.
దానికి సంతోషించి హైదరాబాద్ ప్రభుత్వ శిక్షణ కళాశాల ప్రిన్సిపాల్కు ఇంగ్లాండ్లో ఎం.ఇడి లేదా పి. హెచ్లలో సీట్ ఇప్పించమని, అక్కడ చదువుకోవడానికి ఇక్కడ సెలవు ఇప్పించమని, 6000 అప్పు ఇప్పించమని లేఖ రాశాడు. అతడు యుద్ధ సమయం ముగిసేవరకు పడవలు వెళ్ళవు, అక్కడ సీట్ రావడం కష్టం, అక్కడికి వెళ్ళాలంటే హైదరాబాద్ ప్రభుత్వం అనుమతి ఇవ్వదు.
ఈ మూడు విషయాలు పూర్తి కాకుంటే డబ్బుతో అవసరమే లేదు అని ప్రత్యుత్తరం పంపాడు. హైదరాబాద్ పోలీస్ కమీషనర్ కాదన్నాడు. కో ఆపరేటివ్ బ్యాంకు సెక్రెటరి లోనే లేదన్నాడు. ఇలా అందరూ నిరుత్సాహపరిచారు. అన్నలా భావించే అబ్దుల్ హమీద్ కూడా మొదట పిచ్చి ప్రయత్నం, యుద్ధకాలంలో ఒక నెలలో పాస్పోర్ట్ రావడం అసంభవం అని చెప్పాడు. మీ ఆశీర్వాదం ఉంటే అన్ని అవుతాయని రామకృష్ణయ్య అంటే ఆశీర్వదించి పంపాడు.
లాతూర్ పోలీస్ ఇన్స్పెక్టర్ మీరు ప్రయత్నం చేయండి నా వంతు సహాయం చేస్తానన్నాడు. ఆ కాలంలో పాస్పోర్ట్ పొందడానికి చాలా తతంగం ఉండేది. పాస్పోర్ట్ కోసం జిల్లా అధికారికి దరఖాస్తు చేస్తే ఆయన హోం శాఖకు పంపితే వారు లోకల్ పోలీసు వారికి పరిశీలన కోసం పంపేవారు.
ఇవన్నీ కావడానికి కనీసం ఆరు నెలల కాలం పట్టేది. ఆ తరువాత వారు దానిని బ్రిటీష్ రెసిడెన్సీకి పంపితే వారు పాస్పోర్ట్ మంజూరు చేసేవారు. ఇదంతా జరగడానికి తనకున్న సమయం సరిపోదని తెలిసి కూడా ముద్దు రామకృష్ణయ్య ప్రయత్నాలు ప్రారంభించాడు.
ప్రశ్న 2.
ముద్దు రామకృష్ణయ్య విదేశయాత్రకు పాస్పోర్టు ఎలా లభించింది ?
జవాబు:
పాస్పోర్ట్ దరఖాస్తుకు పెట్టడానికి ఫోటోలు కావాలి. ఫోటోలు దిగడానికి మంచి డ్రెస్ కూడా లేదు. లాతూర్ పోలీస్గా మంచి కాలర్ ఉన్న డ్రెస్తో ఫోటోలు దిగాడు. పాస్పోర్ట్ దరఖాస్తుకు పది రూపాయాల ఫీజు చెల్లించాలి. ఆ డబ్బులను స్కూల్ ఫీ నుండి వాడుకొని జీతం వచ్చాక స్కూల్ వారికి ఇచ్చాడు.
ఆ దరఖాస్తును డిప్యూటి కలెక్టర్ ద్వారా ఉస్మానాబాద్ కలెక్టర్కు పంపాడు. తన పరిస్థితి వివరిస్తూ ఒక ప్రయివేటు లెటర్ రాసి ఒక విద్యార్థి ఇచ్చిన కవర్లో పెట్టి పోస్ట్ చేశారు. ఆ కవర్లో అనుకోకుండా ఒక రూపాయి ఉండిపోయింది. అది తెలిసి కలెక్టర్ శిక్షిస్తాడేమో అని రామకృష్ణయ్య భయపడ్డాడు. సిగ్గుతో ఆ విషయాన్ని ఎవరికీ చెప్పలేదు.
హమీద్ పాస్పోర్ట్ రావడం అంతసులభం కాదని చెప్పేవారు. స్కూల్లో సెలవు తీసుకొని పాస్పోర్ట్ పని మీద హైదరాబాదు వెళ్ళాడు. అక్కడ మున్సిపల్ సత్రంలో సామాను పెట్టి కార్యాలయాలన్నీ తిరిగేవాడు. మొదట బ్రిటీష్ రెసిడెన్సికి వెళ్ళాడు. అక్కడికి ఫైల్ రాలేదని తెలిసి పొలిటికల్ డిపార్ట్మెంటుకు వెళ్ళాడు.
అక్కడ కూడా లేదని తెలిసి అక్కడి నుండి చీఫ్ సూపరింటెండెంట్ కార్యాలయానికి వెళ్ళాడు. అక్కడ మీ దరఖాస్తు లేదని చెప్పారు కాని వెతకమని అడిగితే అక్కడే ఉంది. అయ్యా .దానిని త్వరగా పూర్తి చేయండి చాల త్వరగా నేను వెళ్ళాల్సి ఉంది అని అడిగితే చాలా పెద్ద పని ఉంది కనీసం సంవత్సరం అయినా పడుతుంది. అని చెప్పారు. వారిని బతిమిలాడితే శివలాల్ అనే వారు సి.ఐ.డి. సెక్షన్లో పని చేస్తున్నారు.
వారిని కలిస్తే పని త్వరగా కావచ్చు అని సలహా ఇచ్చారు. దేవునికి నమస్కరించి శివకుమార్ లాలు దగ్గరికి వెళ్ళాడు. వారితో కలిసి పోలీస్ ఇన్స్పెక్టర్ జనరల్ దగ్గరికి వెళ్లి రామకృష్ణయ్య పరిస్థితిని వివరించి పోలీసు రిపోర్ట్ త్వరగా హోం డిపార్ట్మెంట్కు పంపాలని అభ్యర్థించాడు. దానికి అంగీకరించి తన క్లార్క్తో బ్రిటీష్ రెసిడెంట్ కార్యాలయానికి సిఫారసు లేఖను పంపాడు. అక్కడికి వెళ్లి అడిగితే ఇంగ్లాండులో ఏదైనా యూనివర్సిటీలో సీటు వచ్చినట్లు కాగితం చూపమన్నారు.
దానితో అతనిపై బాంబు పడ్డట్లయింది. మీర్ రజా అలీ సహకారంతో రిప్లయ్ పెయిడ్ ఎక్స్ ప్రెస్ టెలిగ్రాం పంపాడు. 48 గంటలు వేచి చూసి తన మిత్రునికి అప్పగించి లాతూరు చేరుకున్నాడు. 72 గంటల తరువాత రిప్లయ్ వచ్చిందని దానిని పాస్పోర్ట్ ఆఫీసులో చూపిస్తే పాస్పోర్ట్ ఇవ్వలేమన్నారని ఉత్తరం వచ్చింది.
చివరి ప్రయత్నంగా హైదరాబాదు వెళ్లి షరతులతో అడ్మిషన్ ఉన్నట్లు వచ్చిన టెలిగ్రాంను, థామస్ కుక్ కంపెనీ వారి లేఖను చూపించి పాస్పోర్ట్ ఇవ్వాలని ‘అభ్యర్థించాడు. రెండు సంవత్సరాలు ఇంగ్లాండులో ఉండడానికి సరిపడా పదివేల రూపాయలను లేదా బ్యాంకు బాలన్స్ను చూపించాలని వారు షరతు విధించారు. మీర్ రజా సహకారంతో ఫస్ట్ క్లాస్ మేజిస్ట్రేట్ గారి సర్టిఫికేట్ చూపించి పాస్పోర్ట్ పొందాడు.
ప్రశ్న 3.
ఇంగ్లండులో ముద్దు రామకృష్ణయ్య విద్యాభ్యాసం ఎలా ప్రారంభమైంది ?
జవాబు:
గ్రేట్ బ్రిటన్ స్కాట్లాండ్లో దిగి అక్కడనుండి ఎడింబరో యూనివర్సిటీ ఉన్న నగరానికి రైలులో వెళ్ళారు. ఆంగ్ల ఉపాధ్యాయునిగా పదకొండు సంవత్సరాల అనుభవం ఉన్నప్పటికీ ఆంగ్లం మాతృభాషగా ఉన్నవారితో మాట్లాడిన అనుభవం లేదు. రిజిస్ట్రార్ దగ్గరకు వెళ్లి టెలిగ్రాఫ్ను చూపించాడు. ఆయన డిపార్ట్మెంట్ ఆఫ్ ఎడ్యుకేషన్తో మాట్లాడుతా అన్నాడు. ఉండడానికి ఒక హోటల్లో రూమ్ బుక్ చేశాడు.
కొన్ని రోజులకు ఆలస్యంగా వచ్చిన కారణంగా అడ్మిషన్ దొరకదు అని చెప్పారు. అక్కడి నుండి లీడ్స్ యూనివర్సిటీలో ప్రయత్నం చేయడానికి లీడ్స్ వెళ్ళాడు. 1939లో చేసిన దరఖాస్తు చేస్తే మీరు రమ్మన్నారు. యుద్ధం కారణంగా ఆలస్యంగా వచ్చాను అని చెప్పాడు. దానికి ఇండియా హౌస్ నుండి దరఖాస్తు చేసుకొమ్మని సలహా ఇచ్చారు. మాది హైదరాబాదు రాజ్యం ఇండియా హౌసుకు సంబంధం ఉండదు అని చెప్తే అడ్మిషన్ అయిన తరువాత వారికి చెప్పొచ్చు అని ఎం.ఇడిలో చేర్చుకున్నారు.
ప్రొఫెసర్ ఫ్రాంక్ ఫీ కట్టడానికి రిజిస్ట్రార్ ఆఫీసుకు వెళ్ళమన్నారు. వారు ఇరవై పౌండ్ల ఫీ కట్టమంటే అంతడబ్బు లేదని చెప్పకుండా పది పౌన్లు ఇప్పుడు కట్టి తరువాత పది పౌన్లు చెల్లిస్తానన్నాడు. దానికి వారు అంగీకరించలేదు. వారం రోజులు గడువు ఇచ్చారు. పడవలో పరిచయమైన సురేశ్ చందరు లేఖ రాశారు.
చివరి తేది ఉదయం పది పౌన్ల పోస్టల్ ఆర్డర్ను సురేశ్ చందర్ పంపాడు. పోస్ట్ ఆఫీసుకు వెళ్లి పది పౌన్లు తీసుకొని మొత్తం ఇరవై పౌన్లు యూనివర్సిటీ అకౌంట్ సెక్షన్ ఇచ్చి రసీదు తీసుకున్నాడు. అలా ఇంగ్లాండ్ లీడ్స్ యూనివర్సిటీలో ఎం. ఇడి. లో అడ్మిషన్ దొరకడంతో ఇంగ్లాండులో ముద్దు రామకృష్ణయ్య విద్యాభ్యాసం ప్రారంభమైనది.

ప్రశ్న 4.
ఇంగ్లండులో ముద్దు రామకృష్ణయ్య విద్యాభ్యాసం ఎలా సాగింది ?
జవాబు:
ఇంగ్లాండ్ లీడ్స్ యూనివర్సిటీలో ఎం.ఇడి.లో ప్రవేశం లభించింది. ప్రొఫెసర్ ఫ్రాంక్ స్మిత్ గైడ్గా ఉన్నారు. ఆయన మాథ్స్, సైకాలజీ, చరిత్రలలో ఏం తీసుకుంటావని అడిగారు. హిస్టరీ ఆఫ్ ఎడ్యుకేషన్ ఇన్ నిజాం స్టేట్ అనే అంశంపై అరవై వేల శబ్దాలతో చరిత్రను రెండు సంవత్సరాలలో రాయాలని నిర్ణయించారు. ప్రొఫెసర్ ఫ్రాంక్ చాలా ప్రేమగా సలహాలు ఇచ్చేవారు. రాసిన వాటిని ఓపికగా సరిదిద్దే వారు.
ముఖ్యంగా ది అనే ఆర్టికల్ వాడటం విషయంలో భారతీయులు పొరపాట్లు చేస్తారని అనేవారు. ఒక గది అద్దెకు తీసుకొని ఉండేవారు. వారికి లభించిన మాంసాహార పదార్థాలు, పంది కొవ్వు ఇంటి ఓనర్కు ఇచ్చి శాఖాహార పదార్థాలు తీసుకునే వారు. పని చేయడానికి ఎంప్లాయ్ మెంటు ఎక్స్ఛేంజ్లో పేరు నమోదు చేసుకున్నారు. రైల్వే పోర్టులో హమాలిగా పని చేసేవారు. దానిలోనుంచి కొంత మొత్తాన్ని ఇంటికి పంపేవారు. డీన్ అనుమతితో లండన్లో కలోనియల్ సెంటర్లో చేరాడు.
కలోనియల్ సెంటర్లోనే నైట్ పోర్టర్గా రాత్రి పది నుండి ఉదయం నాలుగు వరకు పని చేసేవాడు. సాయంత్రం ఆరు నుండి పది వరకు హోటల్ వెయిటర్ గా పని చేసేవాడు. ఉదయం తొమ్మిది నుండి సాయంత్రం ఐదు వరకు లైబ్రరీలో ఐదు నుండి పది వరకు కలోనియల్ సెంటర్లో చదువుకునేవారు. ఉదయం నాలుగు నుండి ఎనిమిది వరకు పడుకునేవారు.
హోటల్లో పని చేసేటప్పుడు హైదరాబాద్ ప్రభుత్వపు అధికారి కలిశారు. వారు ప్రధాని నవాబు చత్తారికి చెప్పి వెయ్యి రూపాయలు పౌండ్లు థామస్ కుక్ ద్వారా పంపించారు. తరువాత బిబిసిలో అసిస్టెంట్ డైరెక్టర్గా ఉద్యోగం లభించింది. ఆ తరువాత వారికి ఆర్ధిక ఇబ్బందులు రాలేదు. బిబిసిలో ఉద్యోగం వచ్చాక ప్రొఫెసర్ ఫ్రాంక్ను కలిసి వారానికి ఒక రోజు వచ్చి పది గంటల క్లాస్ వినడానికి అనుమతి పొందాడు.
మిగతా పనులన్నీ మానేసి బిబిసిలో మాత్రమే పని చేస్తూ శ్రద్ధగా చదువును కొనసాగించాడు. వందల పుస్తకాలు, డాక్యుమెంట్లు చదివి నోట్స్ రాసి ప్రొఫెసర్కు చూపిస్తే ఆయన ప్రేమతో సలహాలు ఇచ్చేవారు. అలా రెండు సంవత్సరాలలో నిజాం రాజ్యంలో విద్య చరిత్ర పేరుతో దక్షిణ భారతదేశ విద్య చరిత్రను రాసి ఎం. ఇడి పూర్తి చేసుకున్నారు.
V. కింది వాటిలో రెండింటికి సందర్భసహిత వ్యాఖ్యలు రాయండి. (2 × 3 = 6)
ప్రశ్న 1.
నుతింపఁగా సకలదైవతకోటులకైన శక్యమే
జవాబు:
కవి పరిచయం : భగీరథ ప్రయత్నం అనే ఈ పాఠ్యభాగాన్ని రాసిన కవి మోతుకూరి పండరీనాథరావు. ఈయన 18వ శతాబ్దం వాడు. ఓరుగల్లు పట్టణానికి సమీపాన గల మడికొండ అతని స్వగ్రామం. ఈ పాఠ్యాంశం శ్రీమత్ పండరీనాథ రామాయణం అనే గ్రంథంలోని బాలకాండ ద్వితీయాశ్వాసంలోనిది. దీనిని శ్రీరామచంద్రునికి అంకితమిచ్చాడు.
అర్థం : కీర్తించడానికి సమస్త దేవ సమూహాలకూ సాధ్యం కాదు.
సందర్భం : ఎంతో తపస్సు చేసి, మరెన్నో అడ్డంకులను అధిగమించి, పాతాళంలో పడిఉన్న తన పితరుల భస్మ రాశులపై గంగను ప్రవహింపజేసిన భగీరథున్ని బ్రహ్మదేవుడు మెచ్చుకుంటున్న సందర్భంలోనిది.
వ్యాఖ్య : బ్రహ్మ భగీరథున్ని కరుణతో చూసి “కుమారా! సగరుడు మొదలైన మీ పూర్వీకులకు ఈ ప్రతిజ్ఞ అనే సముద్రాన్ని తరించడం సాధ్యం కాలేదు. దానిని సాధించిన నిన్ను, నీ తపస్సును మెచ్చుకోవడం సమస్త దేవతా సమూహాలకు కూడా సాధ్యం కాదు” అని అన్నాడు.

ప్రశ్న 2.
ప్రజల యెడ విరోధంబు వాటించుటెంతమేలు
జవాబు:
కవి పరిచయం : ఈ వాక్యం తిక్కన రాసిన మహాభారతం ఉద్యోగపర్వం తృతీయాశ్వాసం నుండి తీసుకున్న శ్రీకృష్ణ రాయబారం అనే పాఠ్యాంశంలోనిది. తిక్కనకు ఉభయకవి మిత్రుడు అనే బిరుదు ఉంది. పదమూడవ శతాబ్దికి చెందిన నెల్లూరు పాలకుడు మనుమసిద్ధి ఆస్థానంలో ఉండేవాడు.
సందర్భం : శ్రీకృష్ణుడు ధృతరాష్ట్రునికి యుద్ధం వల్ల కలిగే నష్టాన్ని వివరిస్తున్న సందర్భంలోనిది.
అర్థం : మీ పిల్లల పట్ల నిర్లక్ష్యం వహించడం సరైనదేనా ?
వివరణ : లోకంలోని రాజులందరూ నీ పాదపీఠాన్ని ప్రీతితో సేవిస్తుండగా సముద్రపు చెలియలికట్టచేత చుట్టబడిన పుడమినంతటిని నీవే ఏకచ్ఛత్రంగా పరిపాలించటం తగును, తల్లి తన బిడ్డలపట్ల శత్రుత్వం వహించటం ఎంత సమంజసమో నీవే ఆలోచించు అని శ్రీకృష్ణుడు ధృతరాష్ట్రునితో అన్నాడు.
ప్రశ్న 3.
మముబెంచు తల్లివై మా పాలవెల్లివై
జవాబు:
కవి పరిచయం : గంగాపురం హనుమచ్ఛర్మ రాసిన దుందుభి కావ్యం నుండి గ్రహించిన దుందుభి అనే పాఠం నుండి తీసుకున్నది ఈ వాక్యం. హనుమచ్ఛర్మ ఉమ్మడి పాలమూరు జిల్లాకు చెందిన కవి.
సందర్భం : ఇక్ష్వాకులు పరిపాలించిన విజయపురాన్ని చేరి, ఆచార్య నాగార్జునున్ని చూసి ధన్యతను పొంది, తెలుగు నేలను పైరు పంటలతో నింపి, శాశ్వతంగా తెలుగు బిడ్డలకు నీ ఆశిస్సులనే అక్షతలను, మంచి నడవడిని అందించి, ఈ లోకంలో, పరలోకంలో అన్ని కోరికలను తీర్చి మమ్మల్ని పెంచే తల్లిగా, మాకు పాల వెల్లిగా ప్రవహిస్తావా ! అని దుందుభిని కవి అడుగుతున్న సందర్భం లోనిది ఈ వాక్యం. అర్థం : మమ్మల్ని పెంచి తల్లివి, మా పాలిట పాల నదివి అని అర్థం.
వివరణ : దుందుభి తెలుగు వారందరికీ తల్లిలాగా పోషణకు కావలిసినవన్నీ ఇస్తుందని భావం.
ప్రశ్న 4.
కల్లాకపటమెరుగని పల్లె ప్రజలే నిన్ను గుర్తించే శ్రోతలు
జవాబు:
కవి పరిచయం : వచన కవితా ప్రవీణ బిరుదాంకితుడైన కనపర్తి రామచంద్రాచార్యులు రాసిన నైమిశారణ్యం అనే కవితా సంపుటి నుండి తీసుకున్న కోకిలా! ఓ కోకిలా అనే పాఠ్యభాగం లోనిది ఈ వాక్యం. రామచంద్రాచార్యులు 48 కావ్యాలు రాశాడు.
సందర్భం : నీ కళకు గుర్తింపు లేని ఈ పట్నంలో ఎందుకు ఉండటం ? నాతో మా పల్లెకు పోదాం రా. అక్కడ ప్రతీచెట్టు నీకు కట్టని వేదికలాగా, పైరగాలి పెట్టని మైకులాగా అబద్దాలు, మోసాలు తెలియని పల్లెజనం నీ కళను ఆస్వాదించే శ్రోతలుగా ఉంటారని కవి చెప్పిన సందర్భంలోనిది ఈ వాక్యం.
అర్థం : అమాయకులైన పల్లె ప్రజలు కోకిల గానాన్ని ఆస్వాదిస్తారని అర్థం.
వ్యాఖ్య : పట్నాలలో భారీ వేదికలు, మైకులు, హంగులు, ఆర్భాటాలు అన్నీ ఉన్నా ఆ కళను ఆస్వాదించే శ్రోతలు లేరని, ఆ లోటు పల్లెటూరిలో తీరుతుందని భావం.
VI. కింది వాటిలో రెండింటికి సందర్భసహిత వ్యాఖ్యలు రాయండి. (2 × 3 = 6)
ప్రశ్న 1.
ఈ మాటతో నా పైన బాంబు పడినంత బాధ అయినది.
జవాబు:
రచయిత పరిచయం: పేదరికంలో పుట్టి, ఎన్నో కష్టాలు అనుభవించి, విదేశాలలో విద్యాభ్యాసం చేసిన విద్యావేత్త ముద్దు రామకృష్ణయ్య. కరీంనగర్ జిల్లా మంథనిలో జన్మించిన ఆయన రాసిన నా ప్రథమ విదేశయాత్ర అనే గ్రంథం నుండి ఇచ్చిన – ఉపవాచకంలోనిది ఈ వాక్యం.
సందర్భం : ఎన్నో ప్రయత్నాల తరువాత పాస్పోర్ట్ మంజూరు చేయమని నిజాం ప్రభుత్వము సిఫారసు లేఖ ఇచ్చింది. ఆ లేఖ తీసుకొని బ్రిటీషు రెసిడెంట్ ఆఫీసుకు వెళ్తే అక్కడున్న అసిస్టెంట్ సెక్రెటరీ ఏదైనా యూనివర్సిటీలో సీటు వచ్చినట్టు కాగితం చూపిస్తేనే పాస్పోర్ట్ ఇస్తామని చెప్పాడు. ఆ మాటతో తనపై బాంబు పడ్డంత పని అయిందని రామకృష్ణయ్య చెప్పిన సందర్భంలోనిది ఈ వాక్యం.
అర్థం : ఆ మాట బాంబు దెబ్బతో సమానం అని అర్థం.
వ్యాఖ్య : ఎంతో కష్టపడ్డ తరువాత వచ్చిన అవకాశం చివరి క్షణంలో చేజారి పోతుందని తెలిసి అది బాంబు పడ్డట్టు అనిపించిందని భావం.
ప్రశ్న 2.
పాలముంచినా నీట ముంచినా నీదే భారం
జవాబు:
రచయిత పరిచయం : పేదరికంలో పుట్టి, ఎన్నో కష్టాలు అనుభవించి, విదేశాలలో విద్యాభ్యాసం చేసిన విద్యావేత్త ముద్దు రామకృష్ణయ్య. కరీంనగర్ జిల్లా మంథనిలో జన్మించిన ఆయన రాసిన నా ప్రథమ విదేశయాత్ర అనే గ్రంథం నుండి ఇచ్చిన ఉపవాచకంలోనిది ఈ వాక్యం.
సందర్భం : అనేక కష్టాల తరువాత విద్యా శాఖనుండి అనుమతి, యూనివర్సిటీలో షరతులతో కూడిన అడ్మిషన్, పాస్పోర్ట్ రావడం ఇలా అనేక పనులు అయినాయి. ఓడ బయలుదేరడానికి వారం రోజుల సమయం మాత్రమే ఉందని థామస్ కుక్ కంపనీ లేఖ పంపింది. కాని అన్నింటికి మించిన డబ్బు సమస్య తీరడం ఎలా అని భగవంతున్ని ప్రార్థించిన సందర్భంలోనిది ఈ వాక్యం.
అర్థం : పాలల్లో ముంచినా నీళ్ళల్లో ముంచినా దేవునిదే భారం అని అర్థం.
వ్యాఖ్య : పాలల్లో ముంచినా అంటే కష్టాలు తీర్చినా, నీళ్ళల్లో ముంచినా అంటే కష్టాల్లోనే ఉంచిన దేవునిదే బాధ్యత అని భావం. అంతా దైవాధీనం అని అంతరార్థం.
ప్రశ్న 3.
వారి ఉచ్ఛారణ, నిత్య వ్యవహారిక శబ్దాలు తెలియవు
జవాబు:
రచయిత పరిచయం : పేదరికంలో పుట్టి, ఎన్నో కష్టాలు అనుభవించి, విదేశాలలో విద్యాభ్యాసం చేసిన విద్యావేత్త ముద్దు రామకృష్ణయ్య. కరీంనగర్ జిల్లా మంథనిలో జన్మించిన ఆయన రాసిన నా ప్రథమ విదేశయాత్ర అనే గ్రంథం నుండి ఇచ్చిన ఉపవాచకంలోనిది ఈ వాక్యం.
సందర్భం : ముద్దు రామకృష్ణయ్య గ్రేట్ బ్రిటన్ స్కాట్లాండ్లో దిగారు. ఎడింబరో యూనివర్సిటీ రిజిస్ట్రార్ కార్యాలయం వెళ్ళాడు. పదకొండు సంవత్సరాల ఆంగ్ల ఉపాధ్యాయ అనుభవం ఉన్నప్పటికీ అక్కడి వారితో ఎప్పుడూ మాట్లాడని కారణంగా వారి భాష, యాస రామకృష్ణయ్యకు కొత్తగా అనిపించిందని చెప్పిన సందర్భంలోనిది ఈ వాక్యం.
అర్థం : ఆంగ్లేయుల ఉచ్ఛారణ వారి వాడుక పదాలు తెలియవు అని అర్థం.
వ్యాఖ్య : ప్రతీ భాషకు స్వంత యాస ఉంటుంది అలానే పలుకుబళ్ళు ఉంటాయి. వాటిని మాతృభాష అయిన వారి లాగా మాట్లాడటం కష్టం అని భావం.
ప్రశ్న 4.
తన సజెషన్స్ ప్రేమతో ఇచ్చేవారు.
జవాబు:
రచయిత పరిచయం : పేదరికంలో పుట్టి, ఎన్నో కష్టాలు అనుభవించి, విదేశాలలో విద్యాభ్యాసం చేసిన విద్యావేత్త ముద్దు రామకృష్ణయ్య. కరీంనగర్ జిల్లా మంథనిలో జన్మించిన ఆయన రాసిన నా ప్రథమ విదేశయాత్ర అనే గ్రంథం నుండి ఇచ్చిన ఉపవాచకంలోనిది ఈ వాక్యం.
సందర్భం : చదువుకోసం ఇంగ్లాండు వచ్చి లీడ్స్ యూనివర్సిటీలో ఎం.ఎడ్. లో చేరాడు. చదువుతో పాటు వివిధ పార్ట్ టైం ఉద్యోగాలు చేశారు. చివరికి లండన్ బిబిసిలో అసిస్టెంట్ డైరెక్టర్గా ఉద్యోగం చేశాడు. అలా ఉద్యోగం చేస్తూ లీడ్స్కు రోజు వెళ్ళడం -సాధ్యం కాదని, వారంలో ఒకరోజు వచ్చి పది గంటలు వింటానని, తన కోసం కొంత శ్రమ తీసుకోవాలని వారి ప్రొఫెసర్ను కోరాడు. దానికి ప్రొఫెసర్ ఫ్రాంక్ అంగీకరించాడని, ప్రేమతో సలహాలు ఇచ్చేవాడని చెప్పిన సందర్భంలోనిది ఈ వాక్యం. అర్థం : ప్రొఫెసర్ ప్రేమగా సలహాలు ఇచ్చారని అర్థం.
వ్యాఖ్య : కష్టపడి చదివే వారికి అందరూ సహకరిస్తారని, అలానే తన ప్రొఫెసర్ కూడా ప్రేమగా సలహాలు ఇచ్చారని భావం.
VII. కింది వాటిలో రెండింటికి సంగ్రహ సమాధానాలు రాయండి. (2 × 2 = 4)
ప్రశ్న 1.
సభలో శ్రీకృష్ణుడు ఎలా ఉన్నాడు ?
జవాబు:
ధృతరాష్ట్రుని సభలో శ్రీకృష్ణుని కంఠస్వరం మేఘ గర్జన లాగా గంభీరంగా, హృదయంగమంగా ఉంది. ఆయన దంతాల కాంతులు మెరుపులవలె ప్రకాశిస్తున్నాయి. వర్షాకాల ప్రకృతి రమణీయతతో శ్రీకృష్ణుణ్ణి తిక్కన పోల్చి ఉపమాలంకారంతో చెప్పాడు. గంభీరమైన సన్నివేశాన్ని గంభీరంగా తిక్కన చిత్రించాడు.
ప్రశ్న 2.
సిద్ధప్ప తన ఆత్మ బంధువులుగా ఎవరిని భావించాడు ?
జవాబు:
వరకవి సిద్ధప్ప వేదాలు తెలిసిన వేమన మా తాతలాంటి వాడు. సురలను ఆనందింప చేసే సుమతి శతక కర్త బద్దెన మా పెద్దమ్మ వంటి వాడు. కాలజ్ఞానాన్ని రాసిన పోతులూరి వీరబ్రహ్మం గారు తండ్రి లాంటి వారు. బ్రహ్మం గారి మనుమరాలు ఈశ్వరమ్మ అక్క లాంటిది. బ్రహ్మంగారి శిష్యుడు సిద్ధప్ప అన్న వంటి వాడు. సంస్కృత కవి కాళిదాసు మా చిన్నన్న. అమర కోశం రాసిన అమరసింహుడు, యాగంటి ఆత్మ బంధువుల వంటి వారు. వీరంతా చనిపోయికూడా జనాల హృదయాలలో బతికే ఉన్నారు అని చెప్పాడు. వీరందరూ వరకవి సిద్ధప్పకు ఆదర్శప్రాయులని సూచించాడు.
ప్రశ్న 3.
కుటుంబ ప్రగతిలో స్త్రీ పాత్రను వివరించండి.
జవాబు:
ఉదయం లేచింది మొదలు ఇల్లు ఊడ్చడం, వాకిలి ఊడ్చి కల్లాపి చల్లడం, వంటపాత్రలు కడిగి వంటచేయడం, అందరి బట్టలుతకడం, వడ్డించి తినేవరకు ఆగి నీ శరీరం మొత్తం అలిసి పోయేదాక పని చేసినా పని అయిపోదు. రోజులో ఉండే ఇరవైనాలుగు గంటలూ కష్టపడ్డా ఇంకా ఎదో ఒకపని ఉండనే ఉంటది. కాని కేవలం ఎనిమిది గంటలు బయట పనికి వెళ్లి వచ్చిన నీ భర్త మాత్రం నీ మీద ఎగిరిఎగిరి పడతాడు. తల్లి అని నిసార్ ఆవేదన వ్యక్తం చేశాడు. ఇంటికి కావలసిన పనులన్ని చేసి, పిల్లలను పోషించి, అత్త మామలను సరిగా పోషించి, భర్త మెప్పును పొంది కూలికి కూడా వెళ్లి పనిచేసి ఆకలితో ఇంటికి వచ్చి పొయ్యి వెలిగిస్తావు. ఏ లెక్కప్రకారం చూసినా ఆడవారు చేసే శ్రమనే అధికం. ఇలా కుటుంబ ప్రగతిలో స్త్రీపాత్ర కీలకం అని నిసార్ తెలిపాడు.
ప్రశ్న 4.
దుందుభితో కవులకున్న సంబంధాన్ని తెలుపండి.
జవాబు:
కత్తిని, కలాన్ని సమానంగా ఉపయోగించి కావ్యాలలోను, ప్రవృత్తిలోను రౌద్ర రసాలను కోరేవారికి ఆనందాన్ని కలిగించేలా చేసిన కళాకారుడైన వీరుడు గోనబుద్ధారెడ్డి. అతని దుందుభి స్నేహం కారణంగా అపూర్వమైన చరిత్ర రంగనాథ రామాయణాన్ని రచించాడు. తెలియని సమయంలో కూడా శైవానికి, వైష్ణవానికి సంబంధించిన అంశాలపై దుందుభి మనస్సులో అనాసక్తత లేదు. మంచి తులసి చెట్ల వరుసలతో, మారేడు వృక్షాల సమూహాలతో రెండు తీరాలను నింపి ఉంచుతూ, తిక్కన కలము చెప్పిన హరి హరాద్వైత తత్వాన్ని తెలుసుకొని సంపన్నురాలుగా ప్రవహిస్తున్నదని చెప్పడం ద్వారా దుందుభికి కవులకు ఉన్న సంబంధాన్ని గంగాపురం హనుమచ్ఛర్మ వివరించాడు.
VIII. కింది వాటిలో రెండింటికి సంగ్రహ సమాధానాలు రాయండి.
ప్రశ్న 1.
బలమైన సంకల్పంతో చేసే కృషి ఎలాంటి ఫలితమిస్తుంది ?
జవాబు:
ఒక చిన్న తుమ్మెద ఆకారానికి ఏరోడైనమిక్ సూత్రాల ఆధారంగా చూస్తే ఆ తుమ్మెద ఎగరడం అసాధ్యమని తెలుస్తుంది. కాని తుమ్మెదలో ఎగరాలనే కోరిక, సంకల్పం ఎంత బలంగా ఉంటాయంటే అది ఎప్పుడూ తన రెక్కలు అల్లాడిస్తూనే ఉంటుంది. అలా పదేపదే తన రెక్కలు కొట్టుకుంటున్నందువల్ల వచ్చే ఉన్నత తరంగదైర్ఘ్య సంవేదనలు ఒక ఆవర్తనాన్ని సృష్టించి దాన్ని ముందుకు తోస్తాయి.
ఆవిధంగా తుమ్మెదకు ఎగరడం సాధ్యమవుతుంది. కాబట్టి బలమైన సంకల్పాలతో చేపట్టే కృషివల్ల సువ్యస్థిత విశ్వాసాలకు (ఎన్నో ఏళ్ల నుండి పాతుకు పోయిన నమ్మకాలకు) నిస్సందేహంగా ఎదురీదగలమని కలాం ప్రబోధించాడు.
ప్రశ్న 2.
ఎలాంటి వారి సాంగత్యము వెంటనే మానుకోవాలి ?
జవాబు:
భాగీరథి తీరంలో మందారవతి అనే వనంలో తిరుగుతున్న జింకను చూసి మోసబుద్ధితో నక్క స్నేహం చేసింది. తన ప్రణాళికలో భాగంగా ఒక పొలం చూపించి యజమాని పన్నిన వలలో చిక్కుకునేల చేసింది. రక్షించమని వేడుకున్నా రక్షించలేదు. సాయంకాలమైనా తన మిత్రుడు ఇంటికి రాకపోయే సరికి కాకి వెతుకుతూ వచ్చి వలలో ఉన్న జింకను చూసింది. నేను ముందే హెచ్చరించినా నామాట వినక పోతివి. మంచివారికి కూడా చెడ్డవారితో అపాయం ఉంటుంది. పోగాలము వచ్చినవారు దీపం ఆరిపోతే వచ్చేవాసనను గుర్తించలేరు. అరుంధతీ నక్షత్రాన్ని చూడలేరు. మిత్రులమాటలు వినరని పెద్దలు చెప్తారు.
ముందర మంచి మాటలు చెప్పి వెనుక మోసం చేసే మిత్రుడు పయోముఖ విషకుంభము వంటివాఁడు. వారితో స్నేహాన్ని వెంటనే మానుకోవాలి. అని చెప్పింది. అది విన్న జింక ఒక నిట్టూర్పు విడిచి “సజ్జన సాంగత్యం వల్ల సర్వశ్రేయములు, దుర్జన సాంగత్యం వల్ల సర్వానర్థాలు కలుగుతాయి అనడానికి ఇదే నిదర్శనం. ఆ జిత్తులమారి నక్క చెప్పిన తేనెమాటలకు మోసపోయాను. మాటల్లో తీపి చూపి లోపల విషముంటదని నేను ఉహించలేదని చెప్పింది.
ప్రశ్న 3.
చిందుల ఎల్లమ్మ ప్రదర్శనలు, పురస్కారాలు తెలుపండి.
జవాబు:
చిందు ఎల్లమ్మ ఇచ్చిన ప్రదర్శనలు : ఎల్లమ్మ నాలుగేళ్ల వయసులోనే బాలకృష్ణుని వేషంతో చిందు యక్షగాన రంగంలో అడుగు పెట్టింది. 1918లో కళారంగంలో ప్రవేశించిన ఎల్లమ్మ గ్రామాల్లో కొన్ని వేల ప్రదర్శనలిచ్చింది. ఎల్లమ్మ తొలి అధికారిక ప్రదర్శన 1979లో నిజామాబాద్ జిల్లా కలెక్టరేట్ లో ఇచ్చింది. మొదటి రాష్ట్రస్థాయి ప్రదర్శన 1980లో రవీంద్రభారతిలో నాటి ముఖ్యమంత్రి సమక్షంలో ఇచ్చింది. 1984వ సంవత్సరంలో మాస్కో నగరంలో తొలి అంతర్జాతీయ ప్రదర్శన ఇచ్చింది. 1986లో ఢిల్లీలో జరిగిన అప్నా ఉత్సవ్ జాతీయ ప్రదర్శన ఇచ్చింది.
ఎల్లమ్మ పొందిన అవార్డులు : చిందు కళలో తన అభినయానికి 1998-99 లో కళారత్న పురస్కారం, 1999లో హంస పురస్కారం, 2004లో రాజీవ్ ప్రతిభా.. పురస్కారాలు అందుకుంది. 1982లో రాష్ట్ర సాహిత్య అకాడమీ విశిష్ట సభ్యత్వం లభించింది. 2004లో అప్పటి ప్రభుత్వం ఆమె గౌరవార్ధం నిజామాబాద్ నుండి బోధన్ వరకు గల రహదారికి ‘ఎల్లమ్మ రహదారి’గా నామకరణం చేసింది.
ప్రశ్న 4.
సురవరం ప్రతాపరెడ్డి సాహిత్యసేవను తెలుపండి.
జవాబు:
సురవరం ప్రతాపరెడ్డి సంపన్న కుటుంబీకులు. బి.ఏ. బి.ఎల్ పట్టభద్రులు. న్యాయవాద వృత్తి చేపట్టడానికి ఎన్నో అవకాశాలు ఉన్నప్పటికి, ప్రభుత్వ ఉద్యోగం కూడా చేయకుండా, జీవితాంతం తెలుగు భాషాభివృద్ధికి కృషి చేసిన త్యాగమూర్తి సురవరం ప్రతాపరెడ్డి. ఈయన బహుభాషావేత్త, అనేక గ్రంథాలు రాశారు. ఉత్తమశ్రేణి పరిశోధకులు, నిర్భయంగా పత్రికను నడిపిన సంపాదకులు.
ఆయన గోలకొండ పత్రిక ద్వారా తెలంగాణా ప్రజలను అన్ని రంగాలలో మేలుకొల్పినారు. గోలకొండ పత్రికా సంపాదకునిగా వీరు వ్రాసిన సంపాదకీయాలు అనేక విషయాలకు విజ్ఞాన నిక్షేపాలవంటివి. రామాయణ రహస్యాలు, హిందువుల పండుగలు, ఆంధ్రుల సాంఘిక చరిత్ర మొదలైన గొప్ప పరిశోధనాత్మకమైన గ్రంథాలను రాశారు. ప్రతాపరెడ్డి మంచికవులు, కథకులు, విమర్శకులు, వ్యాసకర్తలు, బహుముఖ ప్రతిభాసంపన్నులు. వారు రాసిన నిరీక్షణము వంటి కథలు కథానికా వాఙ్మయంలో మొదటి శ్రేణికి చెందిన కథలు. తమ రచనల ద్వారా తెలంగాణా సమాజాన్ని చైతన్యవంతం చేశారు. గోలకొండ కవుల సంచిక ద్వారా తెలంగాణలో మరుగున పడిన శతాధిక కవులను వెలుగులోకి తెచ్చారు.

IX. కింది ప్రశ్నలలో ఆరింటికి ఒక వాక్యంలో సమాధానం రాయండి. (6 × 1 = 6)
ప్రశ్న 1.
దుందుభి ఒడిలో శాంతి పొందినవి ఏవి ?
జవాబు:
దైన్య, శుష్క కంకాలములు. ఎండిన అస్థిపంజరాలు
ప్రశ్న 2.
కనపర్తి రాసిన కోకిల కవిత ఏ కావ్యంలోనిది ?
జవాబు:
నైమిశారణ్యం కవితా సంపుటి లోనిది
ప్రశ్న 3.
నిసార్ ఏ సంస్థకు కార్యదర్శిగా ఉన్నాడు ?
జవాబు:
ప్రజా నాట్యమండలికి
ప్రశ్న 4.
కౌరవ సభకు రాయబారిగా ఎవరు వచ్చారు ?
జవాబు:
శ్రీకృష్ణుడు
ప్రశ్న 5.
‘పండరీనాథ రామాయణం’ ఎవరికి అంకితం ఇచ్చారు ?
జవాబు:
శ్రీరామచంద్రునికి
ప్రశ్న 6.
వరకవి సిద్ధప్పకు ఏయే విద్యలలో ప్రావీణ్యం ఉన్నది?
జవాబు:
జ్యోతిష్యం, ఆయుర్వేదం, వాస్తు యోగ విద్యల్లో
ప్రశ్న 7.
నిసార్ ఏ సంవత్సరం నుంచి పాటలు రాస్తున్నాడు ?
జవాబు:
1986 నుండి
ప్రశ్న 8.
దుందుభి అద్దాన్ని చూసి రూపము దిద్దుకొనేదెవరు ?
జవాబు:
చందమామ
X. కింది ప్రశ్నలలో ఆరింటికి ఒక వాక్యంలో సమాధానం రాయండి. (6 × 1 = 6)
ప్రశ్న 1.
భూపాలరావుకు తెలిసిన భాషలను పేర్కొనండి.
జవాబు:
తెలుగు, సంస్కృతం, కన్నడ, మరాఠి, హిందీ, ఫ్రెంచి, డచ్.
ప్రశ్న 2.
భుజకీర్తులు, కిరీటాలు ఏ కట్టెతో తయారుచేస్తారు ?
జవాబు:
పొనికి లేదా బూరుగు కట్టె.
ప్రశ్న 3.
భారతదేశపు ‘మిస్సైల్ మ్యాన్’ అని ఎవరికి పేరు ?
జవాబు:
ఎ.పి.జె. అబ్దుల్ కలాంకు.
ప్రశ్న 4.
లోకమే కుటుంబమని భావించు వారెవరు ?
జవాబు:
మహాత్ములు
ప్రశ్న 5.
మున్షీ ప్రేమ్చంద్ కథలను మొదటిసారి తెలుగులోకి అనువదించింది ఎవరు ?
జవాబు:
మాడపాటి హనుమంతరావు.
ప్రశ్న 6.
రామరాజు చిన్నప్పటినుండి ఎటువంటి భావాలు ప్రోది చేసుకున్నాడు ?
జవాబు:
దేశభక్తి భావాలు.

ప్రశ్న 7.
‘వింగ్స్ ఆఫ్ ఫైర్’ పుస్తక రచయిత ఎవరు ?
జవాబు:
ఎ.పి.జె. అబ్దుల్ కలాం.
ప్రశ్న 8.
మొహర్రం పదవరోజున ఏ ఉత్సవాలు జరుగుతాయి
జవాబు:
బీబీకా ఆలం, ఏనుగు అంబారీ లంగరు ఉత్సవాలు.
XI. కింది ప్రశ్నలలో ఒక దానికి లక్షణాలు తెలిపి ఉదాహరణతో సమన్వయించండి. (1 × 6 = 6)
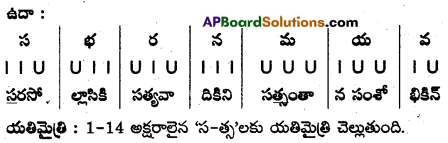
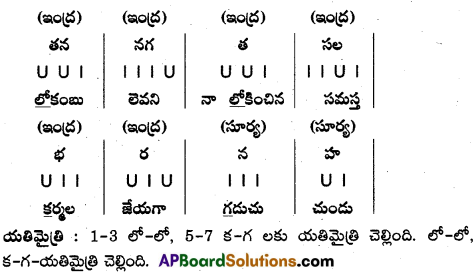
1. మత్తేభం
జవాబు:
- ప్రతి పాదానికి స, భ, ర, న, మ, య, వ అనే గణాలుంటాయి.
- ప్రతి పాదానికి 20 అక్షరాలుంటాయి.
- ప్రతి పాదంలో 14వ అక్షరం యతిమైత్రి కల్గి ఉంటుంది.
- నాలుగు పాదాలకు ‘ప్రాసనియమం’ ఉంటుంది.
- నాలుగు పాదాలకు లక్షణాలు సమానం.
ఉదా :

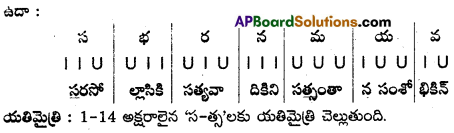
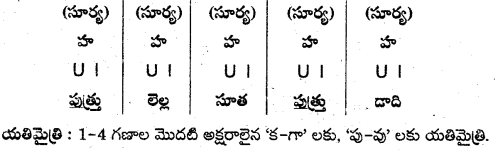
2. తేటగీతి.
జవాబు:
- తేటగీతి పద్యంలో నాలుగు పాదాలు ఉంటాయి.
- ప్రతి పాదానికీ వరుసగా ఒక సూర్యగణం, రెండు ఇంద్రగణాలు, మరల రెండు సూర్యగణాలు ఉంటాయి.
- ప్రతిపాదంలోనూ 1-4 గణాల మొదటి అక్షరానికి యతిమైత్రి ఉంటుంది.
- ప్రాసయతిని పాటింపవచ్చు.
- ప్రాస నియమం ఉండదు.
ఉదా :
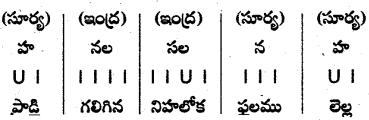
యతిమైత్రి : 1-4 గణాల మొదటి అక్షరాలైన ‘పా – ఫ’ లకు యతిమైత్రి చెల్లింది.
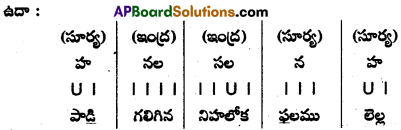
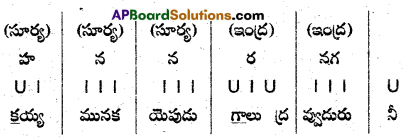
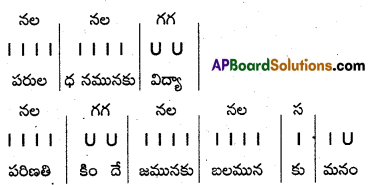
3. ఉత్పలమాల
జవాబు:
- ప్రతి పాదానికి వరుసగా భ, ర, న, భ, భ, ర, వ అనే గణాలుంటాయి.
- ప్రతి పాదానికి ‘20′ అక్షరాలుంటాయి.
- ప్రతి పాదంలో, 10వ అక్షరం యతిమైత్రి కల్గివుంటుంది.
- నాలుగు పాదాల్లో ప్రాస నియమం ఉంటుంది.
- నాలుగు పాదాలకు లక్షణాలు సమానం.
ఉదా :

యతిమైత్రి : 1-10 అక్షరాలైన ‘డ, టా’ లకు యతిమైత్రి చెల్లుతుంది.
XII. కింది ప్రశ్నలలో ఆరింటికి ఒక వాక్యంలో సమాధానం రాయండి. (6 × 1 = 6)
ప్రశ్న 1.
‘ఉత్పలమాల’లో వచ్చే గణాలు ఏవి ?
జవాబు:
ఉత్పలమాలలో ప్రతి పాదములోనూ వరుసగా భ, ర, న, భ, భ, ర, వ అనే గణాలు ఉంటాయి.
ప్రశ్న 2.
‘చంపకమాల’లో వచ్చే గణాలు ఏవి ?
జవాబు:
చంపకమాలలో వచ్చే గణాలు, వరుసగా న, జ, భ, జ, జ, జ, ర అనేవి.
ప్రశ్న 3.
‘ఛందస్సు’ అనగానేమి ?
జవాబు:
పద్య లక్షణాలను తెలిపేది ఛందస్సు. లయ ప్రాధాన్యత, ఛందస్సులో అంతర్గతంగా ఉంటుంది.
ప్రశ్న 4.
‘ఉత్పలమాల’ పద్యంలో ప్రతీ పాదానికి ఎన్ని అక్షరాలు ఉంటాయి ?
జవాబు:
ఉత్పలమాలలో ప్రతి పాదానికీ 20 అక్షరాలు ఉంటాయి.
ప్రశ్న 5.
పద్యాలు ప్రధానంగా ఎన్ని రకాలు ?
జవాబు:
పద్యాలు ప్రధానంగా మూడు రకాలు :
- వృత్తాలు
- జాతులు
- ఉపజాతులు.
ప్రశ్న 6.
‘చంపకమాల’లో ఎన్నవ అక్షరం యతిస్థానం ?
జవాబు:
చంపకమాలలో 11వ అక్షరం యతిస్థానం.
ప్రశ్న 7.
‘చంపకమాల’ పద్యంలో ప్రతి పాదానికి ఎన్ని అక్షరాలు ఉంటాయి
జవాబు:
చంపకమాల పద్యంలో, ప్రతి పాదానికీ 21 అక్షరాలు చొప్పున ఉంటాయి.
ప్రశ్న 8.
సీసపద్యానికి అనుబంధంగా ఉండే పద్యాలు ఏవి ?
జవాబు:
సీసపద్యానికి అనుబంధంగా ఆటవెలది గాని, తేటగీతి గాని ఉంటుంది.
XIII. కింది వాటిలో ఒక దానికి లక్షణాలు తెలిపి ఉదాహరణతో సమన్వయించండి. (1 × 6 = 6)
ప్రశ్న 1.
యమకం
జవాబు:
యమకం : అక్షర సముదాయం అర్థభేదంతో పునరావృతమైనచో దాన్ని
‘యమకాలంకార’ మంటారు.
ఉదాహరణ : లేమా! దనుజుల గెలవగ
లేమా ! నీవేల కడగి లేచితి విటులన్-
లే, మాను ! మాన వేనియు
లే మా విల్లందు కొనుము లీలిన్ లన్.
వివరణ : పై పద్యంలో మొదటి ‘లేమా’ అనేది, స్త్రీ సంబోధన వాచకం. రెండవ ‘లేమా’ అనేది, గెలువలేకపోతామా ? అనే అర్థాన్ని ఇచ్చేది. మూడవచోట, ‘లే’ కు, లెమ్మని, మానుకొమ్మని అర్థం. నాలుగో చోట, లేచి మా విల్లు అందుకొమ్మని ప్రేరేపించటం. అందువల్ల ఇది యమకాలంకారం.

ప్రశ్న 2.
ఉత్ప్రేక్ష
జవాబు:
ఉత్ప్రేక్షాలంకార లక్షణము : ‘ఉత్ప్రేక్ష’ అంటే ఊహించడం అని అర్థం. ధర్మ సామ్యాన్ని బట్టి ఉపమేయాన్ని ఉపమానంగా ఊహించడం ఉత్ప్రేక్షాలంకారం.
ఉదాహరణలు :
- ఆ మేడలు ఆకాశాన్ని ముద్దాడుచున్నవా అన్నట్లున్నవి.
- గాంధీ మహాత్ముని హత్య వల్ల భారతజాతికి కలిగిన దుఃఖాన్ని చూడలేకపోయాడా అన్నట్లుగా సూర్యుడు అస్తమించాడు.
వివరణ : పై రెండు ఉదాహరణలలోనూ, ఊహ ప్రధానంగా ఉన్నది. మేడలు ఆకాశాన్ని ముద్దాడుతున్నట్లు, దుఃఖం చూడలేకనే సూర్యుడు అస్తమించాడా అన్నట్లు, అనే రెండు చోట్లనూ ఊహలే ఉన్నాయి. అందువల్ల, ఇవి ‘ఉత్ప్రేక్షలకు ఉదాహరణలు.
ప్రశ్న 3.
అర్థాంతరన్యాస
జవాబు:
అర్ధాంతరన్యాసాలంకార లక్షణము : సామాన్య వాక్యాన్ని విశేష వాక్యంతోనూ, విశేష వాక్యాన్ని సామాన్య వాక్యంతోనూ, సమర్థించి చెప్పినట్లయితే ‘అర్ధాంతరన్యాసాలంకారము’.
ఉదాహరణ : గాంధీజీ భారతదేశానికి స్వాతంత్ర్యాన్ని సాధించిపెట్టాడు.
మహాత్ములకు సాధ్యము కానిది లోకమున లేదు కదా !
వివరణ : భారతదేశానికి స్వాతంత్య్రం సాధించడం, విశేష విషయము. దాన్ని ‘మహాత్ములకు సాధ్యముకానిది లేదు కదా ! అనే సామాన్య వాక్యంతో సమర్థించడం వల్ల ఇది ‘అర్ధాంతరన్యాసాలంకారం’.
XIV. కింది ప్రశ్నలలో ఆరింటికి ఒక వాక్యంలో సమాధానం రాయండి. (6 × 1 = 6)
ప్రశ్న 1.
ఉపమావాచకాలు ఏవి ?
జవాబు:
పోలె, వలె, బలె, అట్లు, లాగు మొదలైనవి ఉపమావాచకాలు.
ప్రశ్న 2.
ఒకే హల్లు అనేకసార్లు ఆవృతి అయితే అది ఏ అలంకారం ?
జవాబు:
ఒకే హల్లు, అనేకసార్లు ఆవృతి అయితే, అది ‘వృత్త్యనుప్రాస’ అలంకారం.
ప్రశ్న 3.
‘ఉపమానం’ అనగానేమి ?
జవాబు:
‘ఉపమానం’ అనగా, పోల్చు వస్తువు. (ఉదా : ‘హంస’)
ప్రశ్న 4.
‘ఉపమేయం’ అనగానేమి ?
జవాబు:
ఉపమేయం అనగా, వర్ణించు వస్తువు. (ఉదా : ‘రాజు కీర్తి’)
ప్రశ్న 5.
‘ఆ నగరమందలి మేడలు ఆకాశాన్నంటుచున్నవి’ ఏ అలంకారం ?
జవాబు:
ఇది ‘అతిశయోక్తి’ అలంకారం.
ప్రశ్న 6.
‘దుఃఖపుటగ్ని’ ఇందులోని అలంకారాన్ని గుర్తించండి.
జవాబు:
‘దుఃఖపుటగ్ని’ అనే పదములో ‘రూపకాలంకారము’ ఉంది.
ప్రశ్న 7.
‘అతిశయోక్తి’ అనగానేమి ?
జవాబు:
గోరంతను కొండంతలుగా వర్ణించడం, ‘అతిశయోక్తి’.
ప్రశ్న 8.
‘ఉత్ప్రేక్ష’ అనగా అర్థం ఏమిటి ?
జవాబు:
‘ఉత్ప్రేక్ష’ అనగా, ఊహించడం అని అర్థం.
XV. ఈ కింది విషయాన్ని 1/3 వంతు సంక్షిప్తీకరించండి. (1 × 6 = 6)
ఇక నేను తెలుగు సాహిత్య రంగంలో చేసిన పరిశోధన గురించి సంగ్రహంగా మనవి చేస్తాను. హైస్కూలు విద్యార్థిగా ఉండినప్పటినుంచే భారతి తదితర పత్రికల్లో మానవల్లి, వేటూరి, నిడుదవోలు, ఈయుణ్ణి, మల్లంపల్లి వంటి పరిశోధకుల వ్యాసాలు, వారు సంపాదించిన గ్రంథాల పీఠికలు చదవటంచేత వారివలె ఇంతవరకు సాహిత్యలోకానికి తెలియని క్రొత్త విషయాలు చెప్పవలెననే నిశ్చయంతో పరిశోధన రంగంలో అడుగు పెట్టినాను. జానపద విజ్ఞానంలో విశ్వవిద్యాలయ స్థాయి పరిశోధనలో తెలుగులోనే కాదు దక్షిణభారతదేశ భాషలన్నిటిలో నా తెలుగు జానపదగేయ సాహిత్యము మొదటి సిద్ధాంత గ్రంథమైనది..ఆ రంగంలో అనేక జానపదగేయ సంకలనాలు ప్రకటించినాను. తెలుగులోను ఇంగ్లీషులోను జాతీయ అంతర్జాతీయ సదస్సుల్లో పదులకొలది పరిశోధనాత్మకపత్రాలు చదివినాను. ఇంగ్లీషులో ఫోక్ టేల్స్ ఆఫ్ ఏ.పి., ఫోక్ లోర్ ఆఫ్ ఏ.పి., సౌత్ ఇండియన్ ఫోక్ సాంగ్స్, గ్లింప్సెస్ ఇంటూ తెలుగు ఫోక్లోర్ గ్రంథాలు ప్రకటించినాను.
జవాబు:
సంక్షిప్తరూపం : హైస్కూల్ విద్యార్థిగా ఉన్నప్పటినుండే భారతిలాంటి పత్రికల్లో మానవల్లి, వేటూరి, నిడుదవోలు, మల్లంపల్లి వంటి వాళ్ళ వ్యాసాలు చదివాను. అందువల్ల కొత్త సాహిత్య విషయాలు చెప్పాలని పరిశోధక రంగంలో అడుగుపెట్టాను. దక్షిణ భారతదేశ భాషల్లోనే నా తెలుగు జానపదగేయ సాహిత్యం మొదటి సిద్ధాంత గ్రంథం. తెలుగు, ఆంగ్లంలో జాతీయ, అంతర్జాతీయ సదస్సుల్లో ఎన్నో పరిశోధక పత్రాలు చదివాను. ఆంగ్లంలో ‘ఫోక్ టేల్స్ ఆఫ్ ఏ.పి., ఫోక్ లోర్ ఆఫ్ ఏ.పి., సౌత్ ఇండియన్ ఫోక్ సాంగ్స్, గ్లింప్సెస్ ఇంటూ తెలుగు ఫోక్లోర్ గ్రంథాలు ప్రకటించాను.

XVI.
(అ) కింద పేర్కొన్న పదాల ఆధారంగా చేసుకుని విద్యార్థి ప్రిన్సిపాల్ల మధ్య సంభాషణను రాయండి. (1 × 5 = 5)
ఆదాయ పత్రం జారీ కొరకు విజ్ఞాపన చేయడానికి వెళ్ళినపుడు అధికారితో సంభాషణ.
(ఆదాయపత్రం – దరఖాస్తు – జతపరుచు – తహశీల్దార్ – ఉపకారవేతనం)
జవాబు:
(అ) విద్యార్థి : తహశీల్దార్ సర్ నమస్కారం ! నా పేరు శ్రీరాం.
అధికారి : నమస్తే చెప్పు బాబూ, ఏ పనిమీద వచ్చావు ?
విద్యార్థి : ఆదాయపత్రం కొరకు దరఖాస్తు చేసుకుందామని వచ్చాను సార్ !
అధికారి : దరఖాస్తు తెచ్చావా ! వివరాలు అన్నీ ఉన్నాయా ?
విద్యార్థి : ఉన్నాయి సర్ ! సంబంధిత పత్రాలన్నీ జతపరిచాను. ఈ ఆదాయ పత్రం నాకెంతో ఉపయోగపడుతుంది సర్.
అధికారి : ఉపకార వేతనం ఏ రకంగా ఉపయోగిస్తావు శ్రీరాం.
విద్యార్థి : ఉపకార వేతనంతో పుస్తకాలు, దుస్తులు ఇతర వస్తువులు కొనడానికి తల్లిదండ్రులపై ఆధారపడే ఇబ్బంది ఉండదు సర్.
అధికారి : మంచిది ! నేను కూడా ఉపకార వేతనం సాయంతోనే ఎమ్.ఎ. వరకు చదివాను.
విద్యార్థి : అలాగా సర్ ! మరి ఆదాయపత్రం ఎప్పుడు ఇస్తారు ?
అధికారి : రెండు రోజుల్లో.
విద్యార్థి : ధన్యవాదాలు సర్ !
(ఆ) కింది ప్రశ్నలకు ఒక్క వాక్యంలో సమాధానాలు రాయండి. (5 × 1 = 5)
ప్రశ్న 1.
రాము గ్రంథాలయానికి వెళ్ళాడు’ వాక్యంలోని క్రియ ఏమిటి ?
జవాబు:
ఈ వాక్యంలోని క్రియ ‘వెళ్ళాడు’ అనే శబ్దము.
ప్రశ్న 2.
నామవాచకానికి గల మరో పేరు ఏమిటి ?
జవాబు:
నామవాచకానికి గల మరో పేరు, ‘విశేష్యము’.
ప్రశ్న 3.
‘అతడు శ్రీరాముడు’ వాక్యంలో ‘అతడు’ అన్నది ఏ భాషాభాగం ?
జవాబు:
‘అతడు’ అనేది, ‘సర్వనామము’.
ప్రశ్న 4.
అవ్యయానికి ఒక ఉదాహరణ ఇవ్వండి ?
జవాబు:
ఎక్కడ ఆరోగ్యం ఉంటుందో అక్కడ సంపద ఉంటుంది. పై వాక్యంలోని ఎక్కడ, అక్కడ అనేవి అవ్యయాలు.
ప్రశ్న 5.
సర్వనామాల గుణాలను తెలియజేసే వాటిని ఏమంటారు ?
జవాబు:
సర్వనామాల గుణాలను తెలియజేసే పదాలను ‘విశేషణం’ అంటారు.
![]()
![]()
![]()