TS Inter 2nd Year Maths 2A Question Paper May 2018

Thoroughly analyzing TS Inter 2nd Year Maths 2A Model Papers and TS Inter 2nd Year Maths 2A Question Paper May 2018 helps students identify their strengths and weaknesses.

TS Inter 2nd Year Maths 2A Question Paper May 2018

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three Sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer all questions.
• Each question carries two marks.

Question 1.
Write the conjugate of the complex number (2 + 5i)(-4 + 6i).
Solution:
Let Z = (2 + 5i)(-4 + 6i)
= -8 + 12i – 20i + 30i²
= -8 – 8i – 30
= -38 – 8i
∴ Z = -38 – 8i
∴ The conjugate of (2 + 5i)(-4 + 6i) is -38 – 8i.

Question 2.
Express the complex number -√3 + i in modulus-amplitude form.
Solution:
Let Z = -√3 + i
= \(-2\left[\frac{-\sqrt{3}}{2}+i \frac{1}{2}\right]\)
= \(-2\left[\cos \frac{5 \pi}{6}+i \sin \frac{5 \pi}{6}\right]\)
∴ -√3 + i modulus-amplitude form is \(2\left[\cos \frac{5 \pi}{6}+i \sin \frac{5 \pi}{6}\right]\).

Question 3.
If 1, w, w² are the cube roots of unity, then prove that \(\frac{1}{2+w}+\frac{1}{1+2 w}=\frac{1}{1+w}\).
Solution:
Since 1, w, w² are the cube roots of units.
∴ 1 + w + w² = 0 and w³ = 1

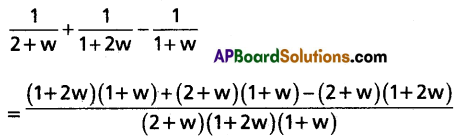
Question 4.
If x² + bx + c = 0, x² + cx + b = 0 (b ≠ c) have a common root, then show that b + c + 1 = 0.
Solution:
Let α be the common root of x² + bx + c = 0 and x² + cx + b = 0
∴ α² + bα + c = 0
α² + cα + b = 0
bα – cα + c – b = 0
⇒ (b – c)α = b – c
⇒ α = 1
∴ 1² + b(1) + c = 0
⇒ 1 + b + c = 0
⇒ b + c + 1 = 0

Question 5.
If 1, 1, α are the roots of x³ – 6x² + 9x – 4 = 0, then find ‘α’.
Solution:
Given 1, 1, α are the roots of x³ – 6x² + 9x – 4 = 0
∴ S₁ = \(\frac{-(-6)}{1}\)
⇒ 1 + 1 + α = 6
⇒ 2 + α = 6
⇒ α = 6 – 2
⇒ α = 4

Question 6.
If ⁿP₃ = 1320, find n.
Solution:
Given ⁿP₃ = 1320
⇒ n(n – 1)(n – 2) = 10 × 132
⇒ n(n – 1)(n – 2) = 10 × 11 × 12
⇒ n(n – 1)(n – 2) = 12 × 11 × 10
⇒ n = 12

Question 7.
If ⁿC₅ = ⁿC₆, then find ¹³C_n.
Solution:
Given ⁿC₅ = ⁿC₆
∴ n = 5 + 6 = 11
¹³C_n = ¹³C₁₁
= ¹³C₂
= \(\frac{13.12}{2}\)
= 78
∴ ¹³C_n = 78

Question 8.
If A and B are coefficients of xn in the expansion of (1 + x)²ⁿ and (1 + x)^2n-1 respectively, then find the value of \(\frac{A}{B}\).
Solution:

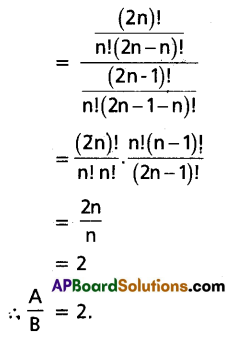
Question 9.
Find the mean deviation about the mean of data 3, 6, 10, 4, 9, 10.
Solution:
Given data 3, 6, 10, 4, 9, 10
Mean = \(\frac{3+6+10+4+9+10}{6}\)
= \(\frac{42}{6}\)
= 7
The absolute values are |3 – 7|, |6 – 7|, |10 – 7|, |4 – 7|, |9 – 7|, |10 – 7| = 4, 1, 3, 3, 2, 3
∴ The mean deviation about the mean = \(\frac{4+1+3+3+2+3}{6}\)
= \(\frac{16}{6}\)
= 2.66

Question 10.
A Poisson Variable satisfies P(X = 1) = P(X = 2). Find P(X = 5).
Solution:
We know P(X = r) = \(\frac{\mathrm{e}^{-\lambda} \cdot \lambda^{\mathrm{r}}}{\mathrm{r} !}\)
Given P(X = 1) = P(X = 2)
∴ \(\frac{\mathrm{e}^{-\lambda} \cdot \lambda^1}{1 !}=\frac{\mathrm{e}^{-\lambda} \cdot \lambda^2}{2 !}\)
⇒ λ = \(\frac{\lambda^2}{2}\)
⇒ 2λ = λ²
⇒ λ² – 2λ = 0
⇒ λ(λ – 2) = 6
Since λ > 0
∴ λ – 2 = 0
⇒ λ = 2

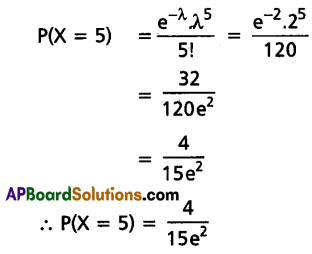
Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Attempt any five questions.
• Each question carries four marks.

Question 11.
Show that the four points in an Argand plane represented by the complex numbers -2 + 7i, \(\frac{-3}{2}+\frac{1}{2} i\), 4 – 3i, \(\frac{7}{2}\)(1 + i) are the vertices of a rhombus.
Solution:
Let A, B, C, D be the points in the Argand plane.


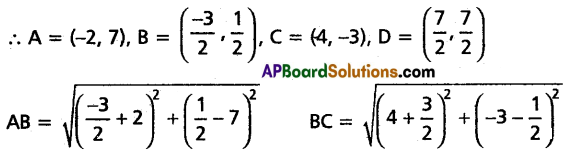
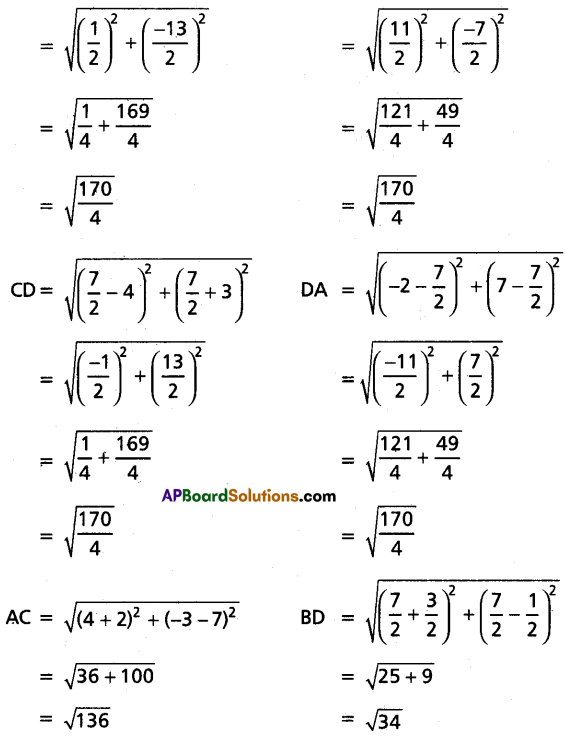
Here AB = BC = CD = DA and AC ≠ BD
∴ ABCD forms a rhombus.

Question 12.
If x is real, prove that \(\frac{x}{x^2-5 x+9}\) lies between \(-\frac{1}{11}\) and 1.
Solution:
Let y = \(\frac{x}{x^2-5 x+9}\)
⇒ yx² – 5xy + 9y = x
⇒ yx² + (-5y – 1)x + 9y = 0
x ∈ R ⇒ (-5y – 1)² – 4 . y . 9y ≥ 0
⇒ 25y² + 10y + 1 – 36y² ≥ 0
⇒ -11y² + 10y + 1 ≥ 0
⇒ 11y² – 10y – 1 ≤ 0
⇒ 11y² – 11y + y – 1 ≤ 0
⇒ 11y(y – 1) + 1(y – 1) ≤ 0
⇒ (11y + 1) (y – 1) ≤ 0
⇒ \(-\frac{1}{11}\) ≤ y ≤ 1
∴ \(\frac{x}{x^2-5 x+9}\) lies between \(-\frac{1}{11}\) and 1.

Question 13.
Find the sum of all 4 digited numbers that can be formed using the digits 0, 2, 4, 7, 8, without repetition.
Solution:
Given digits are 0, 2, 4, 7, 8
Sum of all the 4 digit numbers by the digits 0, 2, 4, 7, 8
= (0 + 2 + 4 + 7 + 8) [^5-1P_4-1 (1111) – ^5-2P_4-2 (111)]
= 21[⁴P₃ (1111) – ³P₂ (111)]
= 21[24(1111) – 6(111)]
= 21[26664 – 666]
= 21[25998]
= 5,45,958

Question 14.
Prove that \({ }^{25} C_4+\sum_{r=0}^4{ }^{(29-r)} C_3={ }^{30} C_4\).
Solution:
L.H.S = \({ }^{25} C_4+\sum_{r=0}^4(29-r) C_3\)

Question 15.
Resolve \(\frac{3 x-18}{x^3(x+3)}\) into partial fractions.
Solution:
Let \(\frac{3 x-18}{x^3(x+3)}=\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x^3}+\frac{D}{x+3}\)
⇒ \(\frac{3 x-18}{x^3(x+3)}=\frac{A x^2(x+3)+B x(x+3)+C(x+3)+D x^3}{x^3(x+3)}\)
⇒ 3x – 18 = Ax² (x + 3) + Bx(x + 3) + C(x + 3) + Dx³ ……….(1)
Put x = 0
0 – 18 = 0 + 0 + C(0 + 3) + 0
⇒ -18 = 3C
⇒ C = -6
Put x = -3
3(-3) – 18 = 0 + 0 + 0 + D(-3)³
⇒ -9 – 18 = D(-27)
⇒ -27 = -27D
⇒ D = 1
Comparing the Co-efficient of x3 terms on both sides in (1)
0 = A + D
⇒ A = -D
⇒ A = -1
Comparing the Co-efficient of x2 terms on both sides in (1)
0 = 3A + B
⇒ B = -3A
⇒ B = -3(1)
⇒ B = -3
∴ A = -1, B = -3, C = -6, D = 1
∴ \(\frac{3 x-18}{x^3(x+3)}=\frac{-1}{x}+\frac{-3}{x^2}+\frac{-6}{x^3}+\frac{1}{x+3}\) = \(\frac{1}{x+3}-\frac{1}{x}-\frac{3}{x^2}-\frac{6}{x^3}\)

Question 16.
If A and B are events with P(A) = 0.5, P(B) = 0.4, and P(A ∩ B) = 0.3. Find the probability that
(i) A does not occur
(ii) Neither A nor B occurs
Solution:
Given P(A) = 0.5, P(B) = 0.4 and P(A ∩ B) = 0.3
(i) The Probability that A does not occur = P(\(\bar{A}\))
= 1 – P(A)
= 1 – 0.5
= 0.5
(ii) The Probability that neither A nor B occurs = P(\(\overline{\mathrm{A}} \cap \overline{\mathrm{B}}\))
= 1 – P(\(\overline{A \cap B}\))
= 1 – P(A ∪ B)
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 – [0.5 + 0.4 – 0.3]
= 1 – 0.6
= 0.4

Question 17.
A and B are independent events with P(A) = 0.2 and P(B) = 0.5. Find
(i) P(A | B)
(ii) P(B | A)
(iii) P(A ∩ B)
(iv) P(A ∪ B)
Solution:
Given P(A) = 0.2, P(B) = 0.5
Since A and B an independent events
(i) P(A | B) = P(A) = 0.2
(ii) P(B | A) = P(B) = 0.5
(iii) P(A ∩ B) = P(A) . P(B)
= (0.2) (0.5)
= 0.1
(iv) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= P(A) + P(B) – P(A) . P(B)
= 0.2 + 0.5 – (0.2) (0.5)
= 0.2 + 0.5 – 0.1
= 0.6

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Attempt any five questions.
• Each question carries seven marks.

Question 18.
If cos α + cos β + cos γ = 0 = sin α + sin β + sin γ then show that
(i) cos 3α + cos 3β + cos 3γ = 3 cos(α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 3 sin(α + β + γ)
Solution:
Given cos α + cos β + cos γ = 0 = sin α + sin β + sin γ
Let a = cos α + i sin α
b = cos β + i sin β
c = cos γ + i sin γ
a + b + c = (cos α + i sin α) + (cos β + i sin β) + (cos γ + i sin γ)
= (cos α + cos β + cos γ) + i(sin α + sin β + sin γ)
= 0 + i(0)
= 0
∴ a + b + c = 0
∴ a³ + b³ + c³ = 3abc
⇒ (cos α + i sin α)³ + (cos β + i sin β)³ + (cos γ + i sin γ)³ = 3(cos α + i sin α) (cos β + i sin β) (cos γ + i sin γ)
⇒ (cos 3α + i sin 3α) + (cos 3β + i sin 3β) + (cos 3γ + i sin 3γ) = 3(cis α) (cis β) (cis γ)
⇒ (cos 3α + cos 3β + cos 3γ) + i(sin 3α + sin 3β + sin 3γ) = 3 cis(α + β + γ)
⇒ (cos 3α + cos 3β + cos 3γ) + i(sin 3α + sin 3β + sin 3γ) = 3[cos(α + β + γ) + i sin(α + β + γ)]
Now, equating real and imaginary parts on both sides, we get
∴ cos 3α + cos 3β + cos 3γ = 3 cos(α + β + γ)
∴ sin 3α + sin 3β + sin 3γ = 3 sin(α + β + γ)

Question 19.
Solve 18x³ + 81x² + 121x + 60 = 0 given that one root is equal to half the sum of the remaining roots.
Solution:
Let α, β, γ be the roots of 18x³ + 81x² + 121x + 60 = 0.

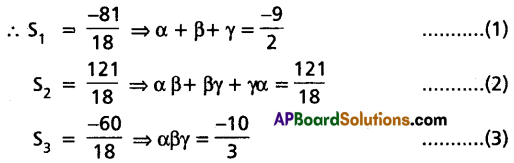
Question 20.
Prove that \(C_0+C_1 \cdot \frac{x}{2}+C_2 \cdot \frac{x^2}{3}+C_3 \cdot \frac{x^3}{4}+\ldots .+C_n \cdot \frac{x^n}{n+1}=\frac{(1+x)^{n+1}-1}{(n+1) x}\)
Solution:

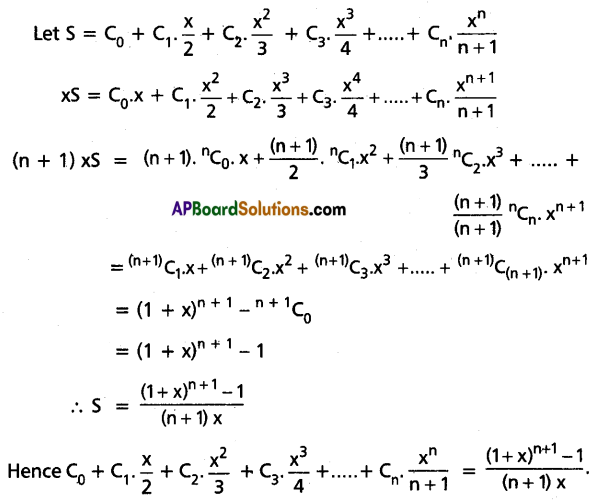
Question 21.
If x = \(\frac{1.3}{3.6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}+\frac{1 \cdot 3 \cdot 5 \cdot 7}{3 \cdot 6 \cdot 9 \cdot 12}\) + ………, then prove that 9x² + 24x = 11.
Solution:


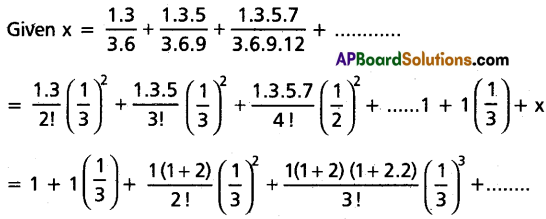
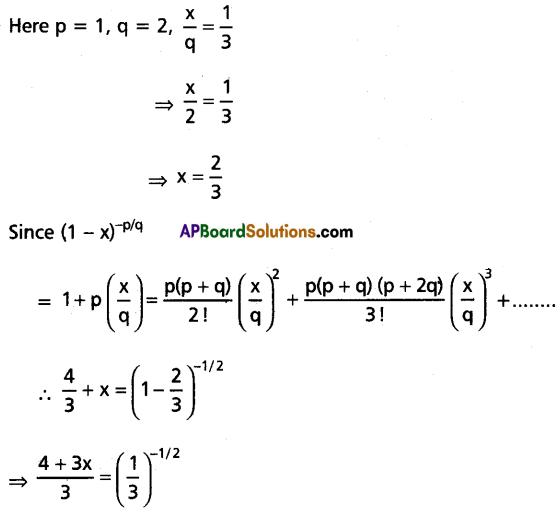
⇒ 4 + 3x = 3√3
⇒ (4 + 3x)² = 27
⇒ 16 + 9x² + 24x = 27
⇒ 9x² + 24x = 11

Question 22.
Find the mean deviation from the mean of the following data, using the step deviation method:

Marks	0-10	10-20	20-30	30-40	40-50	50-60	60-70
No. of Students	6	5	8	15	7	6	3

Solution:
Let assumed mean A = 35 Then d_i = \(\frac{x_i-35}{10}\)

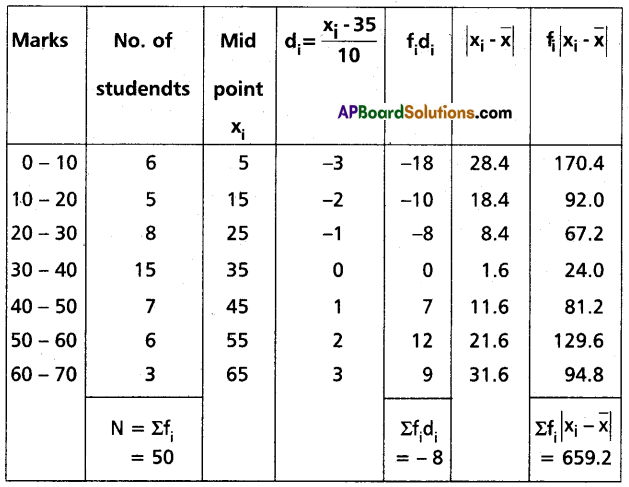
Question 23.
A, B, C are 3 newspapers from a city. 20% of the population read A, 16% read B, 14% read C, 8% both A and B, 5% both A and C, 4% both B and C and 2% all the three. Find the percentage of the population who read atleast one newspaper.
Solution:
Given P(A) = \(\frac{20}{100}\)
P(B) = \(\frac{16}{100}\)
P(C) = \(\frac{14}{100}\)
P(A ∩ B) = \(\frac{8}{100}\)
P(B ∩ C) = \(\frac{4}{100}\)
P(C ∩ A) = \(\frac{5}{100}\)
P(A ∩ B ∩ C) = \(\frac{2}{100}\)
We know P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
= \(\frac{20}{100}+\frac{16}{100}+\frac{14}{100}-\frac{8}{100}-\frac{4}{100}-\frac{5}{100}+\frac{2}{100}\)
= \(\frac{20+16+14-8-4-5+2}{100}\)
= \(\frac{35}{100}\)
∴ The percentage of the population who read atleast one newspaper = \(\frac{35}{100}\) × 100 = 35%

Question 24.
A random variable X has the following probability distribution:

X = x	0	1	2	3	4	5	6	7
P(X = x)	0	k	2k	2k	3k	k2	2k2	7k2 + k

Find (i) k (ii) the mean and (iii) P(0 < X < 5).
Solution:
We know ΣP(X = x) = 1
⇒ 0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
⇒ 10k² + 9k = 1
⇒ 10k² + 9k – 1 = 0
⇒ 10k² + 10k – k – 1 = 0
⇒ 10k(k + 1) – 1(k + 1) = 0
⇒ (10k – 1) (k + 1) = 0
⇒ k = \(\frac{1}{10}\), -1
(i) k = \(\frac{1}{10}\) Since k > 0

(ii) Mean = 0 P(X = 0) + 1 P(X = 1) + 2 P(X = 2) + 3 P(X = 3)+ 4 P(X = 4) + 5 P(X = 5) + 6 P(X = 6) + 7 P(X = 7)
= 0(0) + 1(k) + 2(2k) + 3(2k) + 4(3k) + 5(k²) + 6(2k²) + 7(7k² + k)
= 0 + k + 4k + 6k + 12k + 5k² + 12k² + 49k² + 7k
= 66k² + 30k
= 66(\(\frac{1}{100}\)) + 30(\(\frac{1}{10}\))
= 0.66 + 3
= 3.66

(iii) P(0 < x < 5) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= k + 2k + 2k + 3k
= 8k
= 8(\(\frac{1}{10}\))
= 0.8