TS Inter 1st Year Physics Question Paper May 2019

Thoroughly analyzing TS Inter 1st Year Physics Model Papers and TS Inter 1st Year Physics Question Paper May 2019 helps students identify their strengths and weaknesses.

TS Inter 1st Year Physics Question Paper May 2019

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer all questions.
• Each question carries two marks.
• All are very short answer type questions.

Question 1.
What is Inertia ? What gives the measure of Inertia ?
Answer:
The inability of a body to change its state of rest or state of motion by itself is known as inertia. Mass is a measure of inertia.

Question 2.
If P = 2\(\vec{i}\) + 4\(\vec{j}\) + 14\(\vec{k}\) and Q = 4\(\vec{i}\) + 4\(\vec{j}\) + 10\(\vec{k}\), then find the magnitude of P + Q.
Answer:
\(\vec{P}\) + \(\vec{Q}\) = (2 + 4) \(\vec{i}\) +(4 + 4) \(\vec{j}\) + (10 + 14)
= 6 \(\vec{i}\) + 8\(\vec{j}\) = 24 \(\vec{k}\)
magnitude of \(\vec{P}\) + \(\vec{Q}\) = |\(\vec{P}\) + \(\vec{Q}\) |
= \(\sqrt{36+64+576}\)
= \(\sqrt{676}\)
= 26 units.

Question 3.
Arrange the fundamental force in descending order according to. relative strength.
Answer:
The ordered from strongest to weakest, the forces are :

1. Strong nuclear force.
2. Electromagnetic force.
3. Weak nuclear force.
4. Gravitational force.

Question 4.
Find the relative error in Z, if Z = \(\frac{A^4 B^{1 / 3}}{C^{3 / 2}}\)
Answer:
The relative error in Z is
\(\frac{\Delta \mathrm{z}}{\mathrm{z}}\) = 4(\(\frac{\Delta \mathrm{A}}{\mathrm{A}}\)) + (\(\frac{1}{3}\)) (\(\frac{\Delta \mathrm{B}}{\mathrm{B}}\)) + (\(\frac{\Delta \mathrm{C}}{\mathrm{C}}\)) + (\(\frac{3}{2}\)) (\(\frac{\Delta \mathrm{D}}{\mathrm{D}}\))

Question 5.
What is Magnus Effect ?
Answer:
Magnus effect: A net upward force acting on a spinning bail in air due to pressure difference between lower and upper surfaces is called as dynamic lift. This dynamic lift on the spinning ball is called magnus effect.

Question 6.
Give an expression for the excess pressure in an air bubble inside the liquid.
Answer:
Excess pressure in an air bubble inside the liquid drop
Δ_P = P_i – p_o = \(\frac{2 T}{r}\)
Since it is having only one free surface.
Where T = Surface tension of the liquid
r = radius of the drop.

Question 7.
Explain Global warming.
Answer:
Global warming : Average increase in temperature of earth surface due to green house effect is called as global warming.

Question 8.
State Newton’s law of cooling.
Answer:
The rate of cooling of a hot body is directly proportional to the difference in temperature between the body and its surroundings provided the difference in temperature is small and the nature of the radiating surface remains same”.
– \(\frac{\mathrm{dT}}{\mathrm{dt}}\) ∝ (T – T_s)

Question 9.
When does a real gas behaves like an ideal gas ?
Answer:
A real gas behaves as an ideal gas at low pressure and high temperature.

Question 10.
The absolute temperature of a gas is increased three times. What will be the increase in rms velocity of the gas molecule ?
Answer:
V_rms = \(\sqrt{\frac{3 \mathrm{kT}}{\mathrm{m}}}\)
T₁ = T; T₂ = 3T
\(\frac{V_1}{V_2}=\sqrt{\frac{T_1}{T_2}}\) ⇒ \(\frac{V_1}{V_2}=\sqrt{\frac{T}{3 T}}\)
∴ V₂ = √3 V₁
⇒ ΔV = V₂ – V₁ = √3 V₁ – V₁ = 0.732 V₁.

Section – B (6 × 4 = 24)

Note:

• Answer any six questions.
• Each question carries four marks.
• All are Short Answer type Questions.

Question 11.
A ball is thrown vertically upwards with a velocity of 20 m/s from the top of a multistorey building. The height of the point from where the ball is thrown is 25 m from the ground.
a) How high will the ball rise ?
b) How long will it be before the ball hits the ground ?
(Take g = 10 m/s² actual value of ‘g’ is 9.8 m/s²).
Answer:
Given u = 20 m/s, h = 25m; g = 10 m/s²
a) Maximum height from the top of the building
H = \(\frac{u^2}{2 g}\) = \(\frac{(20)^2}{2 \times 10}\) = 20 m

b) For a body projected from the top of the tower (or) building
h = – ut + \(\frac{1}{2}\) gt²
25 = – 20t + \(\frac{1}{2}\) (10) t² ⇒ 25 = – 20t + 5t²
5t² – 20t – 25 = 0
⇒ 5(t² – 4t – 5) = 0
⇒ t² – 5t + t – 5 = 0 ⇒ t = 5, t = – 1
But time does not take – ve value.
∴ t = 5 sec.

Question 12.
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola.
Answer:
A body projected into path of a projectile is a parabola : Let a body be projected with an initial velocity ‘V_o‘ at angle ‘θ₀‘ with the horizontal, from the point of projection ‘O’.
The horizontal component of velocity u_x = u cos θ
The vertical component of velocity u_y = u sin θ
Let the projectile is at the point P(x, y) after a time interval ‘t’.

i) Along horizontal :
u_x = u cos θ, a_x = 0, S_x = t, t = t
Using S = u_xt + \(\frac{1}{2}\) a_xt² ⇒ x = u cos θ t
⇒ t = \(\frac{\mathrm{x}}{\mathrm{u} \cos \theta}\) ________ (1)

ii) Along the vertical :
u_x = u sin θ, a_y = – g; S_y = y, t = t
Using, S = ut + \(\frac{1}{2}\) at²
y = (u sin θ) t – \(\frac{1}{2}\) gt² ________ (2)

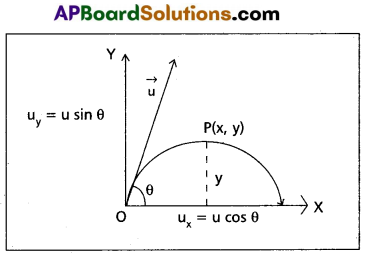
Using equations (1) and (2)
y = (u sin θ) \(\frac{\mathrm{x}}{\mathrm{u} \cos \theta}\) – \(\frac{1}{2}\) g (\(\frac{x^2}{u^2 \cos ^2 \theta}\))
y = tan θ x – (\(\frac{g}{2 u^2 \cos ^2 \theta}\)) x²
Let tan θ = A and \(\frac{g}{2 u^2 \cos ^2 \theta}\) = B
∴ y = Ax – Bx²
This represents the equation of a parabola and hence the path of a projectile is-a parabola.

Question 13.
Define the terms momentum and impulse. A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12 m/s. If the mass of the ball is 0.15 kg, determine the impulse imparted to the ball. (Assume linear motion of the ball).
Answer:
Momentum : The momentum of a body is defined as the product of its mass and velocity.
Impulse : The product of the force and time that product a funite change in momentum of the body is called impulse.
∴ Impulse = F × Δt = m(V – u)
Change in momentum = 0.15 × 12 – (- 0.5 × 12) = 3.5 Ns.
Impulse = 3.5 Ns, in the direction from the batsman to the bowler.
This is an examples where the force on the ball by the batsman and the time of contact of the ball and the bat are difficult to know, but the impulse is readily calculated.

Question 14.
Define angular velocity. Derive V = rω.
Answer:
Angular velocity (ω) : It is defined as rate of change of angular
displacement ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\)

Relation between linear velocity and angular velocity : Let a particle is moving in a circle of radius ‘r’ with constant speed V as shown in fig.

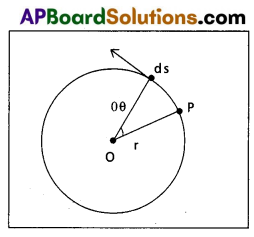
Let the particle P be displaced by ‘ds’ in a time interval ‘dt’ through an angle dθ.
We know that Angle = \(\frac{\text { Arc length }}{\text { radius }}\)
dθ = \(\frac{\mathrm{ds}}{\mathrm{r}}\) ⇒ ds = rdθ
Linear velocity V = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = \(\frac{\mathrm{rd} \theta}{\mathrm{dt}}\) = (∵ \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\) = ω)

Question 15.
Find the torque of a force 7î + 3ĵ – 5k̂ about the origin. The force acts on a particle whose position vector is î – ĵ + k̂.
Answer:
Here r = î – ĵ + k̂ and F = 7î + 3ĵ – 5k̂
We shall use the determinate rule to find the torque

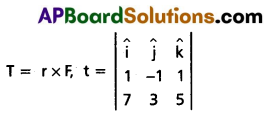
= (5 – 3) î -(- 5 – 7) ĵ + (3 – (- 7))k̂
⇒ T = 2î + 12ĵ + 10k̂.

Question 16.
What is a geo-stationary satellite ? State its uses.
Answer:
Geo-stationary (or) Pola satellite : A satellite whose time period of revolution is equal to that of rotation of earth (24 hours) is called Geostationary satellite.

Uses :
These are used to :

1. Know the shape and size of the earth.
2. Study the changes in the atmosphere.
3. Study the upper regions of the atmosphere.
4. Identify the minerals and natural resources present inside the earth.
5. To transmit the T.V programmes to the distant places.
6. To study the primary cosmic rays.

Question 17.
Define strain energy. Derive an expression for it.
Answer:
Strain energy : The work done in deforming a body is stored as potential energy called strain energy.
Strain energy = \(\frac{1}{2}\) × stress × strain × volume

Derivation : Let a deformation force ‘F’ is applied on a wire of length ‘L’ and area of cross section ‘A’. Let ‘x’ is the elongation produced.
Then F = \(\frac{\mathrm{yAx}}{\mathrm{L}}\)
The work done for the elongation dx is given by
dW = F.dx ⇒ dW = \(\frac{\mathrm{yAx}}{\mathrm{L}}\)dx
The total work done for the elongation ‘x’ is given by

Question 18.
Obtain the relation between Celsius and Fahrenheit scales of temperature. What is the temperature for which the readings on Celsius and Fahrenheit scales are same ?
Answer:
Centigrade (Celsius) scale of temperature : In the centigrade (Celsius) scale of temperature, the lower fixed point is the ice point, and it’s value 0°C. The upper fixed point is the steam point and it’s value 100°C. The interval between these two points (that is 100 – 0 = 100°C) is subdivided into 100 equal parts, each one corresponding to 16C.

Fahrenheit scale of temperature : In the Fahrenheit scale of tem¬perature, the lower fixed point is the ice point and its value is 32°F and the upper fixed point is the steam these two points (that is 212 – 32 = 180°F) is subdivided into 180 equal pbrts. Each on equal to 1°F.

The relation between celsius and Fahrenheit scale is
\(\frac{t_f-32}{180}\) = \(\frac{t_c}{100}\) or \(\frac{t_c}{5}\) = \(\frac{t_f-32}{9}\)
This is written as \(\frac{{ }^{\circ} \mathrm{C}}{5}\) = \(\frac{{ }^{\circ} \mathrm{F}-32}{9}\)
Here is t_F or °F is temperature in Fahrenheit scale and tc (or °C) is temperature in the centigrade (celsius) scale.

Question 19.
Develop the motions of work and kinetic energy and show that it leads to work energy theorem.
Answer:
Work (W) : Work done by the force is defined as the product of component of the force in the direction of the displacement and magnitude of the displacement.
W = (F cos θ) S
= \(\vec{F}\). \(\vec{s}\)

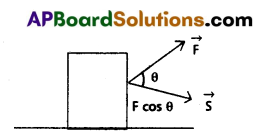
Kinetic energy:
The energy passed by a body by virtue of its motion is called kinetic energy (K). Ex: A bullet fired from a gun, water flowing along a river etc.
K. E. (K) = \(\frac{1}{2}\)mv²

Work – energy theorem : ‘The work done on a particle by the net force is equal to the change in kinetic energy.

Proof : Conservation a body moving with initial velocity ‘u’ and acceleration ‘a’. Let us converts a displacement ‘s’ and its final velocity is V₀ under the constant external force F as shown in figure.

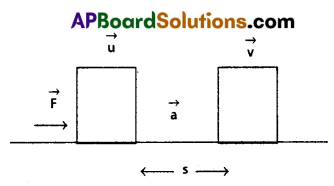
From v² – u² = 2 as ⇒ a = \(\frac{v^2-u^2}{2 a s}\) ________ (1)
The work done by force F is
W = \(\vec{F}\). \(\vec{s}\) = F.S cos θ = mas (∵ F = ma)
⇒ W = m(\(\frac{v^2-u^2}{2 s}\))s =\(\frac{1}{2}\)m (v² – u²)
(or) W = \(\frac{1}{2}\)mv² – \(\frac{1}{2}\)mu²
⇒ W = K_f – K_i = ΔKE
Hence work – energy theorem is proved.

Question 20.
Show that the motion of a simple pendulum is simple harmonic and Hence derive an expression for its time period. What is seconds pendulum ? Find the length of a seconds pendulum.
Answer:

• Consider simple pendulum, a small bob of mass m tied to an in extenside mass less string of length L and other end of the string is fixed from a rigid support.
• Once the bob is slightly displaced and released, it begins to oscillate about mean position.
• Let θ be the angular displacement and T be the tension in the string.
• The forces acting on the bob are
  (a) tension T along the string
  (b) weight mg acts Vertically downwards.
• The force mg can be resolved into two components.
  1. Mg cos θ with balances the tension.
  2. Mg sin θ acts as restoring force normal to length.
• The force mg sin θ will provide the restoring torque, which tends to bring the bob back to its mean position O.

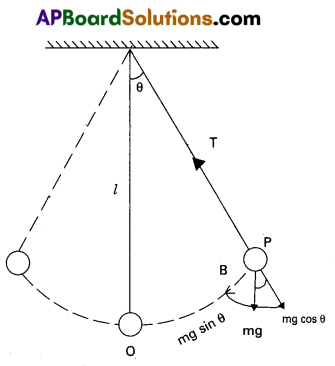
• The restoring torque is given by
  J = Restoring force × ⊥^lar distance
  T = – mg sin θ × L ________ (2)
  For small angles sin θ ≈ θ
  ∴ T = – mg Lθ ________ (3)
  ⇒ I α = – mg Lθ [T = Iα]
  Here moment of inertia I = ML²
  ∴ ML² α = – mgLθ
  ⇒ α = – (\(\frac{g}{L}\))θ ________ (4)
  Thus simple pendulum executes angular S.H.M and hence comparing equation (4) with equation of SHM
  α = – ω²θ
  We get, ω² = \(\frac{g}{L}\) ⇒ ω = \(\sqrt{\frac{g}{L}}\)
  Time period (T) = \(\frac{2 \pi}{\omega}\) = \(\frac{2 \pi}{\sqrt{\frac{g}{L}}}\) = 2π\(\sqrt{\frac{L}{g}}\)
  Second’s pendulum : A pendulum whose time period is 2 seconds is called seconds pendulum.

Question 21.
Explain reversible and irreversible processes. Describe the working of Carnot engine. Obtain an expression for the efficiency.
Answer:
Reversible process : A process that can be retraced back in the opposite direction in such away that the system passes through the same states as in the direct process, and finally the system and the surroundings return in their original states, is called a reversible process.

Examples :

1. Diffusion of gasues.
2. Magnetization of material.
3. Work done against friction.

Carnot Engine Definition : A reversible heat engine operating between two temperatures is caleld a carnote engine.

Carnot’s heat engine : Carnot ideal heat engine consists of four components.

1) Cylinder : Cylinder, whose walls are perfectly non-conductive and base, is perfectly conducting fitted with a non-conducting frictionl&ss movable piston.

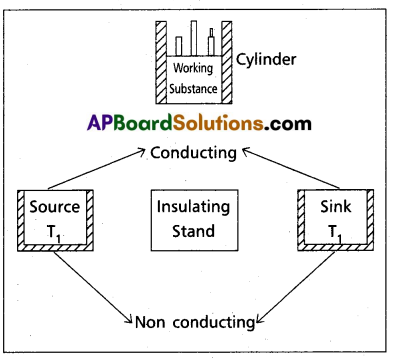
2) Source : It is at a high temperature T₁K and has infinite thermal capacity.

3) Sink : It is at a lower temperature T₂K and has infinite thermal capacity.

4) Insulating stand : It is a perfectly non-conducting stand on which the cylinder containing the working substance can be put and it can be made perfectly insulated from the surroundings.
Consoled 1 mole of an ideal gas filled in the cylinder at absolute temperature T₁ Pressure P₁ Volume V₁.
The working substance (perfect gas) in the cylinder is subjected to cycle of four operations and it is known as Carnot cycle.

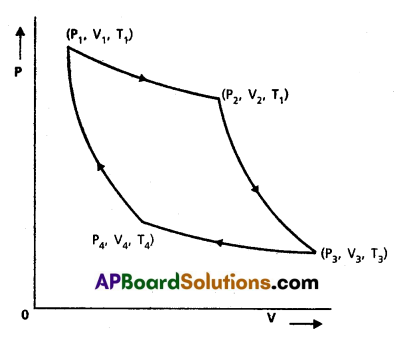
Operation 1 : Isothermal Expansion (AB) : The cylinder containing ideal gas as working substance allowed to expand slowly at this constant temperature T₁.
W₁ = Q₁ = RT₁ log_e(\(\frac{V_2}{V_1}\)) ________ (1)

Operation 2 : Adiabatic expansion (BC): The cylinder is than placed on the non-conducting stand and gas is allowed to expand adiabatically till the temperature falls from T₁ and T₂.
W₂ = \(\frac{\mathrm{R}\left(\mathrm{T}_1-\mathrm{T}_2\right)}{\gamma-1}\) ________ (2)

Operation 3 : Isothermal compression (CD) : The cylinder is placed on the skin and the gas is compressed at constant temperature T₂.
Work done = Heat released by the system
⇒ W₃ = Q₃ = RT₂ log_e(\(\frac{V_4}{V_3}\))
⇒ W₄ = Q₄ = RT₂ log_e(\(\frac{V_3}{V_4}\))

Operation (4) : Adiabatic compression (DA) : Finally the cylinder is again placed on non-conducting stand and the compression is continued so that gas returns to its initial stage.
W₄ = \(\frac{R\left(T_2-T_1\right)}{\gamma-1}\) = \(\frac{R\left(T_1-T_2\right)}{\gamma-1}\)
Efficiency of Carnot cycle : The efficiency of engine is defined as the ratio of work done to the heat supplied i.e.,
η = \(\frac{\text { Work done }}{\text { Heat input }}=\frac{W}{Q_1}\)
Net-work done during the complete cycle
W = W₁ + W₂ + W₃ + W₄