TS Inter 1st Year Maths 1B Question Paper May 2017

Access to a variety of TS Inter 1st Year Maths 1B Model Papers and TS Inter 1st Year Maths 1B Question Paper May 2017 allows students to familiarize themselves with different question patterns.

TS Inter 1st Year Maths 1B Question Paper May 2017

Time : 3 Hours
Max. Marks : 75

Note : This question paper consists of THREE sections A, B and C.

Section – A
(10 × 2 = 20 Marks)

I. Very short answer type questions :

1. Answer all the questions.
2. Each question carries two marks.

Question 1.
Transform the equation 3x + 4y + 12 = 0 into normal form.
Solution:
Given straight line equation is 3x + 4y + 12 = 0
⇒ 3x + 4y = -12
⇒ -3x – 4y = 12
⇒ \(\left(\frac{-3}{5}\right) x+\left(\frac{-4}{5}\right) y\) = \(\frac{12}{5}\)
⇒ x cos α + y sin α = \(\frac{12}{5}\)
Where cos α = \(\frac{-3}{5}\) and Sinα = \(\frac{-4}{5}\)
Which is in the normal form.

Question 2.
If the straight lines x + p =0, y + 2 = 0 and 3x + 2y + 5 = 0 are concurrent, then find the value of p.
Solution:
Given straight line equations are
x + P = 0 ….. (1)
y + 2 = 0 ….. (2)
3x + 2y + 5 = 0 ….. (3)
Solving (1) and (2), we get
X = -p, y = -2
∴ The point of intersection of (1) and (2) is (-p, -2)
Since (1), (2), (3) are concurrent The point (-p, -2) lies on (3)
∴ 3(-p) + 2 (-2) + 5 = 0
⇒ -3P – 4 + 5 = 0
⇒ 3P = 1 ⇒ P = \(\frac{1}{3}\).

Question 3.
Find the ratio in which XZ – plane divides the line joining A (-2, 3, 4) and B (1, 2, 3).
Solution:
Given A = (-2, 3, 4)
B = (1, 2, 3)
The ratio in which xz-plane divides the line joining A, B is -y₁ : y₂
= -3 : 2
= 3 : 2 externally

Question 4.
Find the equation of the plane if the foot of the perpendicular from origin to the plane is (2, 3, -5).
Solution:
Let P = (2, 3, -5)
Since P is the foot of the perpendicular from origin to the required plane
∴ \(\overline{O P}\) is perpendicular to the required plane.
∴ D.rs of \(\overline{O P}\) = (2 – 0, 3 – 0, -5 – 0)
= (2, 3, -5)
Hence equation to required plane is
2(x – 2) + 3(y – 3) – 5(z + 5) = 0
⇒ 2x – 4 + 3y – 9 – 5z – 25 = 0
⇒ 2x + 3y – 5z – 38 = 0

Question 5.
Compute

Solution:

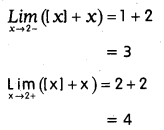
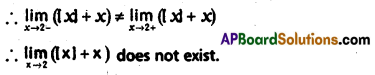
Question 6.
Evaluate

Solution:

Question 7.
If y = Cosec^-1 (e^2x+1), find \(\frac{d y}{d x}\).
Solution:

Question 8.
Show that, y = x + Tanx satisfies Cos²x\(\frac{d^2 y}{d x^2}\) + 2x = 2y .
Solution:

Question 9.
Find the approximate value of \(\sqrt[4]{17}\).
Solution:

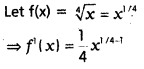
Question 10.
If 0 ≤ x ≤ \(\frac{\pi}{2}\), then show that x ≥ Sinx.
Solution:
Let f(x) = x – sinx
f’(x) = 1 – Cosx ≥ 0 ∀ x
∴ f is an increasing function for all x
∴ f ≥ 0 6
⇒ x – sinx ≥ 0 – sin 0
⇒ x – sinx ≥ 0
⇒ x ≥ sinx

Section – B

II. Short Answer Type Questions. (5 × 4 = 20)

1. Attempt any five questions.
2. Each question carries four marks.

Question 11.
A (5, 3) and B (3, -2) are two fixed points. Find the equation of the locus of P, so that the area of the triangle PAB is 9.
Solution:
Given A = (5, 3)
B = (3, – 2)
Let P(x₁, y₁) be any point on the locus.
Given geometric condition is area of ∆PAB is 9.

Question 12.
Show that the axes are to be rotated through an angle of \(\frac{1}{2}\)Tan^-1\(\left(\frac{2 h}{a-b}\right)\) so as to remove the xy term from the equation ax² + 2hxy + by² = 0, if a ≠ b and through an angle \(\frac{\pi}{4}\), if a = b.
Solution:
If the axes are rotated through an angle ‘θ’, then
x = x’ cos θ – y’ sin θ
y = x’ sin θ + y’ cos θ
Therefore the given equation transforms as
a (x’ cos θ – y’ sin θ)² + 2h (x‘ cos θ – y’ sin θ) (x’ sin θ + y’ cos θ) + b (x’ sin θ – y’ cos θ)² = 0
To remove x’y’ term from the equation, the coefficient of x’y’ term must be zero.
So, (b – a) sin θ cos θ + h(cos²θ – sin²θ) = 0

Question 13.
Find the value of k, if the angle between the straight lines 4x – y + 7 = 0 and kx – 5y – 9 = 0 is 45°.
Solution:
Given straight line equations are
4x – y + 7 = 0 …….. (1)
kx – 5y – 9 = 0 ……. (2)
The angle between (1) and (2) is 45°.

⇒ 17k² + 425 = 32k² + 80k + 50
⇒ 15k² + 80k – 375 = 0
⇒ 3k² + 16k – 75 = 0
⇒ 3k² + 25k – 9k – 75 = 0
⇒ k(3k + 25) -3 (3k + 25) = 0
⇒ (k – 3)(3k + 25) = 0
⇒ k = 3 (or) \(\frac{-25}{3}\)

Question 14.
Show that

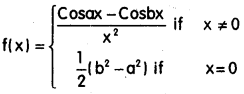
Where a and b are real constants,, is continuous at 0.
Solution:

Question 15.
If xy = e^x-y, then show that \(\frac{d y}{d x}\) = \(\frac{\log x}{(1+\log x)^2}\).
Solution:
Given x^y = e^x-y
Taking logarithms on bothsides, we have

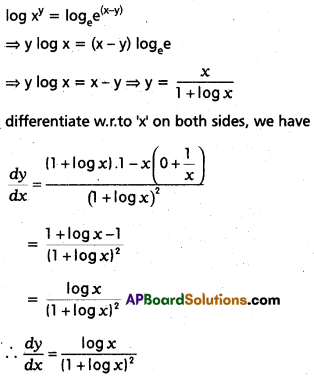
Question 16.
At any point t on the curve x = a (t + Sint), y = a (1 – Cost), find the lengths of tangent and normal.
Solution:
Equation of the curve is x = a (t + sin t), y = a (1 – cos t)

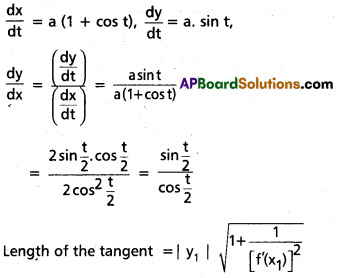
Question 17.
A container is in the shape of an inverted cone has height 8 m and radius 6 m at the top. If it is filled with water at the rate of 2 m³/minute, how fast is the height of water changing when the level is 4 m ?
Solution:
Let OC be the height of the water level at t sec.

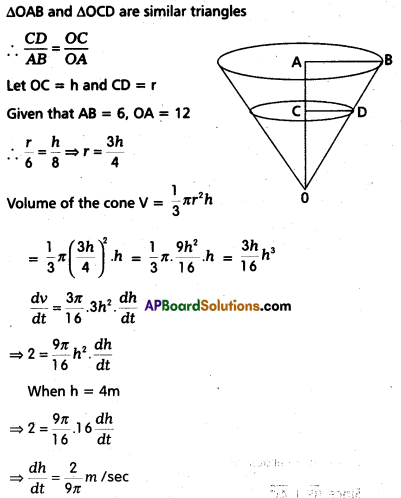
Section – C

III. Long Answer Type Questions. (5 × 7 = 35)

1. Attempt any five questions.
2. Each question carries seven marks.

Question 18.
Find the orthocenter of the triangle whose vertices are (-5, -7), (13, 2) and (-5, 6).
Solution:
Let A = (-5, -7)
B = (13, 2)
C = (-5, 6)
Let \(\overline{\mathrm{AD}}\) be the perpendicular drawn from A to \(\overline{\mathrm{BC}}\) and \(\overline{\mathrm{BE}}\) be the perpendicular drawn from B to \(\overline{\mathrm{AC}}\).

From (1)
9x – 2(2) + 31 = 0 ⇒ 9x + 27 = 0
⇒ 9x = -27
⇒ x = -3
∴ x = -3 and y = 2
∴ Ortho center H = (-3, 2)

Question 19.
If (α, β) is the centroid of the triangle formed by the lines ax² + 2hxy + by² = 0 and lx + my =1, then prove that
\(\frac{\alpha}{b l-h m}\) = \(\frac{\beta}{a m-h l}\) = \(\frac{2}{3\left(b l^2-2 h l m+a m^2\right)}\)
Solution:
Let ax² + 2hxy + by² = 0 represent the lines
l₁x + m₁y = 0 ….. (1)
l₂x + m₂y = 0 ……. (2)
Given line is lx + my = 1 ………. (3)
∴ ax² + 2hxy + by² = (l₁x + m₁y) (l₂x + m₂y)
Comparing both sides, we have
l₁l₂ = a, m₁m₂ = b, l₁m₂ + l₂m₁ = 2h
Clearly the point of intersection of (1) and (2) is 0(0, 0)
Let A be the point of intersection of (1) and (3)

General centroid of ∆OAB is (α, β)

Question 20.
Find the value of k, if the lines joining the origin to the points of intersection of the curve 2x² – 2xy + 3y² + 2x – y – 1 = 0 and the line x + 2y = k are mutually perpendicular.
Solution:

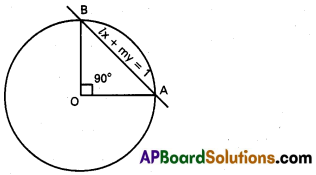
Equation of the circle is x² + y² = a² ….. (1)
Equation of AB is lx+ my = 1 ……. (2)
Homogenising (1) with the help of (2)
Combined equation of OA, OB is
x² + y² = a².1²
x² + y² = a² (lx + my)²
= a²(l²x² + m²y² + 2lmxy)
= a²l²x² + a²m²y² + 2a²lmxy
i.e., a²l²x² + 2a²lmxy + a² m²y² – x² – y² = 0
(a²l² – 1) x² + 2a²lmxy + (a²m² – 1) y² = o
Since OA, OB are perpendicular
Co-efficient of x² + co-efficient of y² = 0
a²l² – 1 + a²m² – 1 = 0
a²(l² + m²) = 2
This is the required condition.

Question 21.
Find the direction cosines of two lines which are connected by the relations l + m + n = 0 and mn – 2nl – 2lm = 0.
Solution:
Given l + m + n = 0 …… (1)
mn – 2nl – 2lm = 0 ……… (2)
From (1), l = -(m + n)
Substituting in (2),
mn + 2n(m + n) + 2m(m + n) = 0
mn + 2mn + 2n² + 2m² + 2mn = 0
2m² + 5mn + 2n² = 0
(2m + n) (m + 2n) = 0
2m = -n or m = -2n

Case (i): 2m₁ = -n₁
From l₁ = -m₁ – n₁
= -m₁ + 2m₁ = m₁
\(\frac{l_1}{1}\) = \(\frac{m_1}{1}\) = \(\frac{x_1}{-2}\)
D.Rs of the first line are 1, 1, -2
D.Cs of this line are \(\frac{1}{\sqrt{6}}\), \(\frac{-2}{\sqrt{6}}\), \(\frac{1}{\sqrt{6}}\)

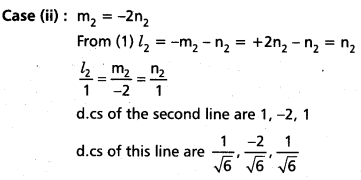
Question 22.
If f(x) = Sin^-1\(\sqrt{\frac{x-\beta}{\alpha-\beta}}\) and g(x) = Tan^-1\(\sqrt{\frac{x-\beta}{\alpha-x}}\) then show that f'(x) = g'(x) (β < x < α).
Solution:
Given f(x) = Sin^-1\(\sqrt{\frac{x-\beta}{\alpha-\beta}}\)
differentiate w.r.to x on both sides, we have

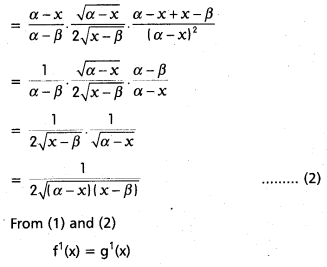
Question 23.
If the tangent at any point on the curve x^2/3 + y^2/3 = a^2/3 intersects the coordinate axes in A and B, then show that the length AB is a constant.
Solution:
Equation of the curve is x^2/3 + y^2/3 = a^2/3
Differentiating w.r.to x

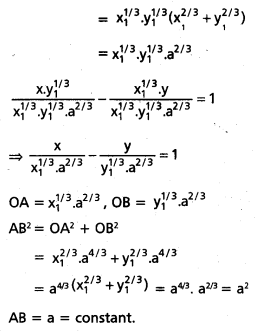
Question 24.
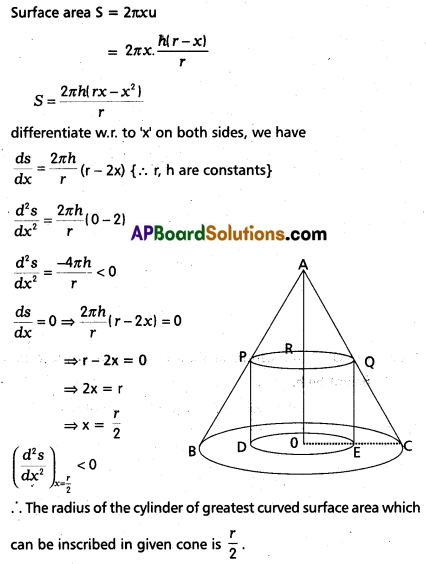
Prove that the radius of the right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone.
Solution:
Let ‘O’ be the centre of the circular base of the cone and its height be h.
Let r be the radius of the circular base of the cone.
Let a cylinder with radius x(OE) be inscribed in the given cone and its height be u.
i.e. PD = RO = QE = u
From big ∆AOC and ∆QEC are similar.
∴ \(\frac{Q E}{O A}\) = \(\frac{E C}{O C}\)
⇒ \(\frac{u}{h}\) = \(\frac{r-x}{r}\)
⇒ u = \(\frac{h(r-x)}{r}\)