TS Inter 1st Year Physics Question Paper May 2018

Thoroughly analyzing TS Inter 1st Year Physics Model Papers and TS Inter 1st Year Physics Question Paper May 2018 helps students identify their strengths and weaknesses.

TS Inter 1st Year Physics Question Paper May 2018

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer all questions.
• Each question carries two marks.
• All are Very Short Answer Type Questions.

Question 1.
What are the fundamental forces in nature ?
Answer:
Fundamental forces in nature are :

1. Gravitational forces
2. Electromagnetic forces
3. Strong nuclear forces and
4. Weak nuclear forces.

Question 2.
Distinguish between accuracy and precision.
Answer:

Accuracy	Precision
1. The accuracy of a measurement of any physical quantity made by any measuring instrument is a measure of how close the measured value is to the true value of the quantity.	1. The precision of the measuring instrument denotes up to what limit (or) resolution the quantity can be measured with the given instruments.
2. The accuracy depends on errors.	2. The precision does not depend on errors.

Question 3.
The vertical component of a vector is equal to its horizontal component. What is the angle made by the vector with x-axis ?
Answer:

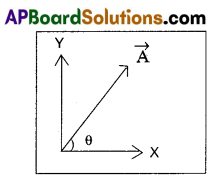
Horizontal component of vector \(\vec{A}\) = vertical
Component of vector \(\vec{A}\)
A cos θ = A sin θ
Tan θ = 1 ⇒ θ = 45°
∴ Angle made by vector A with X – axis, θ = 45°.

Question 4.
If a bomb at rest explodes into two pieces, the pieces travel in opposite directions. Explain.
Answer:
According to law of conservation of momentum,
Initial momentum of bomb = Final momentum of bomb.

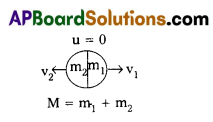
MU = n₁ v₁ + m₂ v₂
O = m₁ v₁ + m₂ v₂
m₁ v₁ = – m₂ v₂
Therefore, two pieces must travel in opposite directions.

Question 5.
Define viscosity. What are the units of co-efficient of viscosity ?
Answer:
Viscosity : The property of a liquid which opposes the relative motion between its layers is called viscosity.
C.G.S unit : poise ; SI unit : Nm^-2 S.

Question 6.
Why are liquid drops and soap bubbles spherical ?
Answer:
The surface tension of a liquid tends to have minimum surface area. For a given volume, the surface area is minimum for a sphere. Hence rain drops are spherical shape.

Question 7.
Can a substance contract on heating ? Give an example.
Answer:
Yes, Rubber, type metal, cast iron are contract on heating.

Question 8.
State the different modes of transmission of heat. Which of these modes require medium ?
Answer:
Different modes of transmission of heat are :

1. Conduction
2. Convection and
3. Radiation.
   conduction and convection modes requires medium.

Question 9.
When does a real gas behave like an ideal gas ?
Answer:
At low pressure and high temperatures real gases behaves like an ideal gas.

Question 10.
Define mean free path.
Answer:
The average distance covered by a molecule between two successive collisions is called the mean free path.

Section – B (6 × 4 = 24)

Note :

• Answer any six of the following questions.
• Each question carries four marks.
• All are Short Answer Type Questions.

Question 11.
A car travels the first third of a distance with a speed of 10 kmph, the second third at 20 kmph and the last third at 60 kmph, What is its mean speed over the entire distance ?
Answer:
V₁ = 10 km ph ; V₂ = 20 km ph ; V₃ = 60 km ph ; V = ?

∴ V = 18 kmph.

Question 12.
If |\(\vec{a}\) + \(\vec{b}\)|= |\(\vec{a}\) – \(\vec{b}\)|, prove that the angle between \(\vec{a}\) and \(\vec{b}\) is 90°.
Answer:
Given, |\(\vec{a}\) + \(\vec{b}\)|= |\(\vec{a}\) – \(\vec{b}\)|
⇒ a² + b² + 2ab cos θ = a² + b² – 2ab cos θ
⇒ 4ab cos θ = a
⇒ cos θ = 0
⇒ cos θ = cos 90°
∴ θ = 90°
Hence angle between \(\vec{a}\) and \(\vec{b}\) is 90°.

Question 13.
Define the terms momentum and impulse. State and ex-plain the law of conservation of momentum.
Answer:
Momentum : The product of mass and velocity of a body is called momentum.
Momentum p = mv
Impulse : The product of force and time that produces finite change in momentum of the body is called impulse.
Impulse (I) = Force × time duration = mat = m \(\frac{(v-u)}{t}\)t
= (mv – mu)

Law of conservation of linear momentum : The total momentum of an isolated system of interacting particles remains constant if there is no resultant external force acting on it.

Explanation : Consider two smooth, non-rotating spheres of masses m₁ and m₂(m₁ > m₂). Let u₁ and u₂ be their initial velocities. Let v₁ and v₂ be final velocities after head on collision. According to law of conservation of linear momentum, we have Momentum of the system before collision – Momentum of the system after collision, i.e., m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
Examples :

1. Motion of a Rocket
2. Bullet – Gun motion.

Question 14.
Distinguish between centre of mass and centre of gravity.
Answer:

Centre of mass	Centre of Gravity
1. A point inside the boundary of a body at which the whole mass is supposed to be concentrated. A force applied at this point produces translatory motion.	1. A point through which the weight of the body acts.
2. It pertains to mass of the body.	2. It refers to weight acting on all particles of the body.
3. In case of small bodies centre of mass and centre of gravity coincide.	3. In case of a huge body centre of mass and centre of gravity do not coincide.
4. The position of C.M. is independent of acceleration due to gravity.	4. The position of C.G. depends upon acceleration due to gravity.
5. Algebraic sum of moments of masses about centre of mass is zero.	5. Algebraic sum of moments of weights about centre of gravity is zero.
6. Centre of mass is used to describe the nature of motion of a body as a whole.	6. Centre of gravity is used to know the stability of the body where it is to be supported.

Question 15.
Define vector product. Explain the properties of a vector product with an example.
Answer:
The cross product of two vectors is given by \(\vec{C}\) = \(\vec{A}\) × \(\vec{B}\) . The magnitude of the vector defined from cross product of two vectors is equal to product of magnitudes of the vectors and sine of angle between the vectors.

Direction of the vectors is given by right hand corkscrew rule and is perpendicular to the plane containing the vectors
∴ |\(\vec{C}\)| = AB sin θ and \(\vec{C}\) = AB sin θ n̂. Where, n̂ is the unit vector perpendicular to the plane containing the vectors \(\vec{A}\) and \(\vec{B}\).

Example :
1) Torque is cross product of position vector and Force.
i.e., \(\vec{T}\) = \(\vec{r}\) × \(\vec{F}\).

2) Angular momentum is cross product of position vector and momentum i.e., \(\vec{L}\) = \(\vec{r}\) × \(\vec{p}\)

Properties :
1) Cross product does not obey commutative law. But its magnitude obey’s commutative low.
\(\vec{A}\) × \(\vec{B}\) ≠ \(\vec{B}\) × \(\vec{A}\) ⇒ (\(\vec{A}\) × \(\vec{B}\)) = – (\(\vec{B}\) × \(\vec{A}\)) , |(\(\vec{A}\) × \(\vec{B}\))| = (\(\vec{B}\) × \(\vec{A}\))

2) It obeys distributive law \(\vec{A}\) × (\(\vec{B}\) × \(\vec{C}\)) = \(\vec{A}\) × \(\vec{B}\) + \(\vec{A}\) × \(\vec{C}\)

3) The magnitude of cross product of two vectors which are parallel is zero.
Since θ = 0; |\(\vec{A}\) × \(\vec{B}\)| = AB sin 0° = 0

4) For perpendicular vectors, θ = 90°, |\(\vec{A}\) × \(\vec{B}\)| = AB sin 90° | n| = AB

Question 16.
What is a geostationary satellite ? State its uses.
Answer:
Geo-stationary satellite : If the period of revolution of an artificial satellite is equal to the period of rotation of earth, then such a satellite is called geo-stationary satellite.
Time period of geo-stationary satellite is 24 hours.

Uses:

1. Study the upper layers of atmosphere.
2. Forecast the changes in atmosphere.
3. know the shape and size of the earth.
4. Identify the minerals and natural resources present inside and on the surface of the earth.
5. Transmit the TV programmes to distant objects.
6. Under take space research i.e. to know about the planets, satellites, comets etc.

Polar satellites : Polar satellites are low altitude satellites (500 to 800km), but they go around the poles of the earth in a north south direction. Its time period is around 100 minutes.

Uses :

1. Polar satellites can view polar and equatorial regions at close distances with good resolution.
2. These satellites are extremely useful for remote sensing, meterology as well as environmental studies of the earth.

Question 17.
Define strain energy and derive an expression for it.
Answer:
The potential energy stored in a body when stretched is called strain energy.
Let us consider a wire of length L and cross – sectional area A. Let x be the change in length of the wire by the application of stretching force F.
Young’s modulus = \(\frac{\text { Longitudinal Stress }}{\text { Longitudinal Strain }}\)
y = \(\frac{\mathrm{FL}}{\mathrm{Ax}}\)
F = \(\frac{y A x}{L}\) ……….. (1)
To stretch the wire further by dx, the workdone dw = F.dx;
dw = F.dx;
dw = (\(\frac{y A x}{L}\))dx
Total workdone to stretch the wire from 0 to x is given by

w = \(\frac{1}{2}\)F.x = \(\frac{1}{2}\) × stretching force × elongation
The work done is stored in the form of potential energy.
u = \(\frac{1}{2}\).Fx. …….. (2)
Strain energy per unit volume = \(\frac{1}{2}\) × \(\frac{F x}{A L}\)
= \(\frac{1}{2}\) × stress × strain.

Question 18.
In what way is the anomalous behaviour of water advantageous to aquatic animals?
Answer:

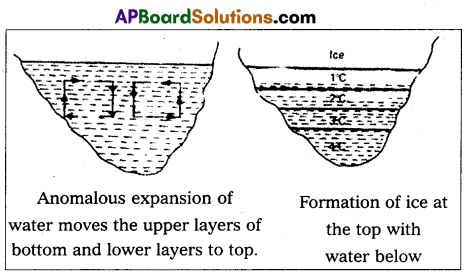
In cold countries, as atmospheric temperature decreases, the upper layers of the lakes, rivers etc., cool, contract and sink to the bottom (fig). This goes on until the whole of the water reaches the temperature of 4°C. When the top layers cool further temperature falls below 4°C, it expands and becomes lighter. It does not sink downwards and remains at the top. With further cooling the top layer gradually form ice at the top (fig). Ice and water are bad conductors of heat. So the lower layers are protected against freezing by the layers of ice and cold water at 1°C, 2°C and 3°C. This results in water remaining at the bottom at 4°C. So that aquatic animals survive in those layers of water.

Section – C (2 × 8 = 16)

Note :

• Answer any two of the following questions.
• Each question carries eight marks.
• All are Long Answer Type Questions.

Question 19.
State and prove law of conservation of energy in case of a freely falling body. A machine gun fires 360 bullets per minute and each bullet travels with a velocity of 600 ms^-1. If the mass of each bullet is 5 gm, find the power of machine gun.
Answer:
Statement : Energy can neither be created nor destroyed, But it can be converted from one form to another form. The total energy of a system always remains constant.

Verification in the case of freely falling body: Let a body of mass’m’ be at height h above the ground. When it is freely falling with an acceleration due to gravity g, the potential energy gradually decreases and at the same time the K.E. of the body increases.

When the body is at A :
At the highest point final velocity v = 0
Kinetic energy K.E. = \(\frac{1}{2}\) mv² = 0
Potential energy P.E. = mgh
Total energy at A =E = RE + K.E.
= mgh + 0
∴ Total energy at A, E = mgh ……….. (1)

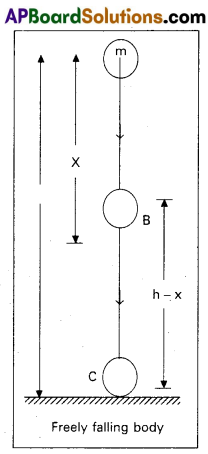
When the body is at B : As the body falls freely, after travelling a distance x, reaches the point B.
At ‘B’ the body possesses both P.E. and K.E.
Potential energy P.E. = mg(h – x)
P.E. = mgh – mgx
Kinetic energy K.E. = \(\frac{1}{2} m v_1^2\)
∴ Total energy at B = P.E. + K.E.
= mgh – mgx + \(\frac{1}{2} m v_1^2\)
For freely falling body
s = x
u = 0
v = v₁
a = g
Sub, these values in equation
v² – u² = 2as
\(v_1^2\) – 0² = 2gs
\(v_1^2\) – 0² = 2gx
\(v_1^2\) = 2gx
Total energy at
B = mgh – mgx + \(\frac{1}{2}\) m. 2gx
= mgh – mgx + mgx = mgh
∴ Total energy of BE = mgh ………. (2)

When the body is at C : The body falls through a distance of ‘h’ and touches the ground at C with a velocity v₂.
Potential energy (P.E.) at C = mg = 0
Kinetic energy K.E. = \(\frac{1}{2} m v_2^2\)
Total energy at C = 0 + \(\frac{1}{2} m v_2^2\) = \(\frac{1}{2} m v_2^2\)
For freely falling body s = h, u = 0, v = v₂ a = g
Sub. these values in equation. v² – u² = 2as ; \(v_2^2\) – 0² = 2gh
\(v_2^2\) = 2gh
Sub this value in total energy we get
Total energy at C = \(\frac{1}{2} m v_2^2\) = \(\frac{1}{2}\) m 2gh
∴ Total energy at C E = mgh
In the above three cases total energy of the body is proved constant. Hence law of conservation of energy is proved.

Problem :
Solution:
No. of bullets (n) = 360
Velocity (V) = 600 ms^-1
Mass (m) = 5 gm = \(\frac{5}{1000}\)kg
Time (t) = 1 min = 60 sec
Power (P) = \(\frac{1}{2}\) \(\frac{\mathrm{mnV}^2}{\mathrm{t}}\)
\(\frac{1}{2}\) × \(\frac{\frac{5}{1000} \times 360 \times(600)^2}{60}\)
= 5,400 watts
= 5.4 K.W.

Question 20.
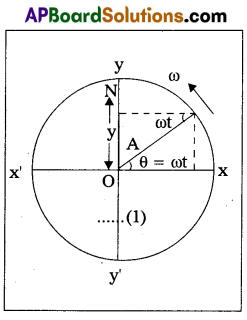
Define simple harmonic motion. Show that the motion of (point) projection of a particle performing uniform circular motion on any diameter is simple harmonic.
Answer:
Consider a particle P moving on the circumference of a circle of radius A with uniform angular velocity ω. Let O be the centre of the circle. XX’ and YY’ are two mutually perpendicular diameters of the circle as shown in the figure. Let PN be drawn perpendicular to the diameter YY’ from P. As P moves on the circumference of the circle, N moves on the diameter YY’ to and fro about the centre O.

Let us consider the position of N at any time t, after leaving the point ‘O’, during its motion. The corresponding angular displacement of the particle P is
∠XOP = θ = ωt.
From Δ^leONP,
sin ωt = \(\frac{\mathrm{ON}}{\mathrm{OP}}\)
ON = OP sin ωt
(∵ ON = y, OP = A)
y = A sin ωt
Differentiating equation (1) w.r.t’t’, we get velocity


From equation (4)
a ∝ -y
Hence acceleration is directly proportional to the displacement and opposite in direction.
Hence motion of ‘N’ is simple harmonic.

Question 21.
State Second law of thermodynamics. How is heat engine different from a refrigerator ?
Answer:
1. Kelvin – planck statement: “No process is possible whose sole result is the absorption of heat from a reservoir and the complete conversion of the heat into work”. (Or) “It is impossible to derive a continuous supply of engines in cooling a body below the coldest of its surroundings”,

2. Clasius statement : “No process is possible whose sole result is the transfer of heat form a colder object to a hotter object”. (Or) “Heat cannot itself flow from cold body to hot body”.

Heat engine : A device which converts heat energy into work is called heat engine.
A heat engine consists of the essential parts.

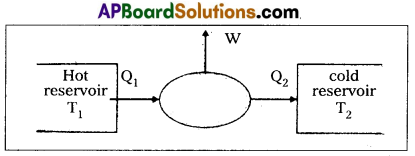
1. Source or hot reservoir : It is maintained at a very high temperature T₁ Heat is extracted from this body.
2. Working substance: In a steam engine working substance is steam. In diesel engine working substance is mixture of fuel vapour and air.
3. Sink or cold reservoir : It is maintained at a very low temperature T₂. It absorbs heat energy, rejected by working substance.

Work done : The difference of heat absorbed from source and heat rejected to sink is equal to work done by the engine. i.e., W = Q₁ – Q₂.

Efficiency : The ratio of workdone (W) by the engine to the amount of heat absorbed (Q₁) by the engine is called efficiency.
i.e., η = \(\frac{\mathrm{W}}{\mathrm{Q}_1}=\frac{\mathrm{Q}_1-\mathrm{Q}_2}{\mathrm{Q}_1}\) = 1 – \(\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\)

Refrigerator : Refrigerator is a heat pump which is the re verse of a heat engine.

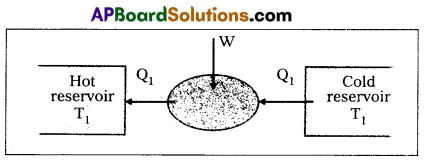
In refrigerator the working substance extracts (Q₂) an amount of heat from sink of lower temperature and a external work W is done on the working substance and finally amount of heat (Q₁) is transferred to source.
The coefficient fo performance (α) of a refrigerator is given by
α = \(\frac{Q_2}{W}=\frac{Q_2}{Q_1-Q_2}\) heat released Q₁ = Q₂ + W
For heat engine η can never exceed 1. For refrigerator α can be greater than 1. Therefore working of refrigerator is opposite to that of heat engine.