TS Inter 1st Year Physics Question Paper March 2020

Thoroughly analyzing TS Inter 1st Year Physics Model Papers and TS Inter 1st Year Physics Question Paper March 2020 helps students identify their strengths and weaknesses.

TS Inter 1st Year Physics Question Paper March 2020

Section – A (10 × 2 = 20)

Note :

• Answer ALL the questions.
• Each question carries TWO marks.
• ALL are very short answer type questions.

Question 1.
What is the discovery of C.V. Raman ?
Answer:
In elastic scattering of light by molecules.

Question 2.
The percentage error in the mass and speed are 2% and 3% respectively. What is the maximum error in kinetic energy ? Calculate using these quantities.
Answer:
\(\frac{\Delta \mathrm{M}}{\mathrm{M}}\) × 100 = 2%, \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100 = 3%;
Kinetic energy = \(\frac{1}{2}\) mV²
\(\frac{\Delta \mathrm{K}}{\mathrm{K}}\) × 100 = \(\frac{\Delta \mathrm{M}}{\mathrm{M}}\) × 100 + 2 \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100
= 2 + 2(3) = 26 = 8%.

Question 3.
\(\vec{A}\) = \(\vec{i}\) + \(\vec{j}\). What is the angle between the vector and x – axis ?
Answer:
\(\vec{A}\) = \(\vec{i}\) + \(\vec{j}\)
cos α = \(\frac{A x}{|A|}\) (∵ A_x = 1)
= \(\frac{1}{\sqrt{1^2+1^2}}\) = \(\frac{1}{\sqrt{2}}\)
α = cos^-1 (\(\frac{1}{\sqrt{2}}\)) = 45°

Question 4.
A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12 ms^-1. If the mass of the ball is 0.15 kg, determine the impulse imparted to the ball. (Assume linear motion of the ball)
Answer:
Change in momentum
= 0.15 × 12 -(- 0.15 × 12) = 3.6 N s
Impulse = 3.6 N s, in the direction from the batsman to the bowler.
This is an example where the force on the ball by the batsman and the time of contact of the ball and the bat are difficult to know, but the impulse is readily calculated.

Question 5.
Give the expression for the excess pressure in an air bubble inside the liquid.
Answer:
Express pressure in an air bubble inside the liquid, P_i – p₀ = \(\frac{2 \mathrm{~s}}{\mathrm{r}}\)
Where s = Surface tension
r = Radius of the air bubble.
Air bubble forms inside the liquid, hence it has one liquid surface.

Question 6.
What is angle of contact ?
Answer:
The angle between tangent to the liquid surface at the point of contact and solid surface inside the liquid is termed as angle of contact (θ).

Question 7.
State Wien’s displacement law.
Answer:
The wavelength (λ_m). corresponding to maximum energy emitted by a black body is inversely proportional to its absolute temperature
(T). i.e., λ_m α \(\frac{1}{\mathrm{~T}}\)

Question 8.
Distinguish between heat and temperature.
Answer:

Heat	Temperature
1. It is a form of energy	1. It is a degree of hotness or coldness of a body.
2. It is the cause on the body.	2. It is an effect on a body.
3. It is determined with calorimeter.	3. It is measured with thermometer.
4. It’s unit is Joule and Calories.	4. It’s unit is degree Celsius or Kelvin or degree Fahrenheit.

Question 9.
State Dalton’s law of partial pressure.
Answer:
The total pressure exerted by a mixture of non-reacting gases occupying a vessel is equal to the sum of the individual pressures which each gas would exert, if it is alone occupied the whole vessel.
i.e., P = P₁ + P₂ + ……..

Question 10.
The absolute temperature of a gas is increased 3 times. What will be the increase in rms velocity of the gas molecule ?
Answer:
Case (i) : The r.m.s velocity of gas molecule, \(\overline{\mathbf{V}}_1\) = \(\sqrt{\frac{3 \mathrm{RT}_1}{\mathrm{M}}}\)

Case (ii) : The r.m.s velocity of gas molecule, \(\overline{\mathbf{V}}_2\) = \(\sqrt{\frac{3 \mathrm{RT}_2}{\mathrm{M}}}\)
\(\frac{\overline{\mathrm{V}}_2}{\overline{\mathrm{V}}_1}\) = \(\sqrt{\frac{\mathrm{T}_2}{\mathrm{~T}_1}}\) = \(\sqrt{\frac{3 \mathrm{~T}_1}{\mathrm{~T}_1}}\) [∵ T₂ = 3T₁] ⇒ \(\overline{\mathbf{V}}_2\) = √3\(\overline{\mathbf{V}}_1\) = 1.732 \(\overline{\mathbf{V}}_1\)
∴ Increase in r.m.s velocity of gas molecule = \(\overline{\mathbf{V}}_2\) – \(\overline{\mathbf{V}}_1\) = 1.732 \(\overline{\mathbf{V}}_1\) – \(\overline{\mathbf{V}}_1\) – = 0.732 \(\overline{\mathbf{V}}_1\)

Section – B (6 × 4 = 24)

Note :

• Answer ANY SIX questions.
• Each question carries FOUR marks.
• ALL are short answer type questions.

Question 11.
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 kmh^-1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 kmh^-1. What is the magnitude of average velocity and average speed of the man over the time interval 0 to 50 min ?
Solution:
Time taken by man to go from his home to market
t₁ = \(\frac{\text { Distance }}{\text { Speed }}\) = \(\frac{2.5}{5}\) = \(\frac{1}{2}\) h
Time taken by man to go from market to his home
t₂ = \(\frac{2.5}{7.5}\) = \(\frac{1}{3}\) h
Total time taken = t₁ + t₂ = \(\frac{1}{2}\) + \(\frac{1}{3}\) = \(\frac{5}{6}\)
h = 50 min.

i) 0 to 30 min
a) Average velocity = \(\frac{\text { Displacement }}{\text { Time }}\) = \(\frac{2.5}{1 / 2}\) = 5 km/h
b) Average speed = \(\frac{\text { Distance }}{\text { Speed }}\) = \(\frac{2.5}{1 / 2}\) = 5 km/h

ii) 0 to 50 min
Total distance travelled = 2.5 + 2.5 = 5 km
Total displacement = zero

a) Average velocity = \(\frac{\text { Displacement }}{\text { Time }}\) = 0
b) Average speed = \(\frac{\text { Distance }}{\text { Speed }}\) = \(\frac{5}{5 / 6}\) = 6 km/h

iii) 0 to 40 min
Distance moved in 30 min (from home to market) = 2.5 km Distance moved in 10 min (from market to home) with speed
7.5 km/h = 7.5 × \(\frac{10}{60}\)
= 12.5 km
So displacement = 2.5 – 1.25 = 1.25 km
Distance travelled = 2.5 + 1.25 = 3.75 km
a) Avg velocity = \(\frac{1.25}{(40 / 60)}\) = 1.875 km/h
b) Avg speed = \(\frac{3.75}{(40 / 60)}\) = 5.625 km/h

Question 12.
State Parallelogram law of vectors. Derive an expression for the magnitude and direction of the resultant vector.
Answer:
Statement : If two vectors acting at a point are represented by the adjacent sides of a parallelogram in magnitude and direction, then their resultant is represented by the diagonal of the parallelogram in magnitude and direction drawn from the same point.

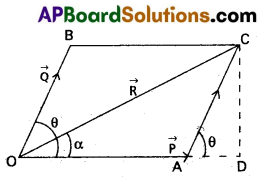
Explanation : Let two forces \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) act at a point O. Let θ be the angle between two forces. Let the side OA = \(\overrightarrow{\mathrm{P}}\) and OB = \(\overrightarrow{\mathrm{Q}}\). The parallelogram OACB is completed. The points O and C are joined. Now OC = \(\overrightarrow{\mathrm{R}}\)

Resultant magnitude :
In fig \(\overrightarrow{\mathrm{OA}}\) = \(\overrightarrow{\mathrm{P}}\) \(\overrightarrow{\mathrm{OB}}\) = \(\overrightarrow{\mathrm{Q}}\), \(\overrightarrow{\mathrm{OC}}\) = \(\overrightarrow{\mathrm{R}}\)
In the triangle COD, OC² = OD² + CD²
OC² = (OA + AD)² + CD² (∵ OD = OA + AD)
OC² = OA² + AD² + 20A. AD + CD62²
OC² = OA² + AC² + 20A. AD ……. (1)
From Δ^le CAD, AD² + CD² = AC²
From Δ^le CAD, cos θ = \(\frac{A D}{A C}\)
AD = AC cos θ
∴ R² = p² + Q² + 2PQ cosθ ………….. (2)
R = \(\sqrt{\mathrm{P}^2+\mathrm{Q}^2+2 \mathrm{PQ} \cos \theta}\) ………… (3)

Resultant direction :
Let α be the angle made by the resultant vector \(\overrightarrow{\mathrm{R}}\) with \(\overrightarrow{\mathrm{P}}\)
Then tan α = \(\frac{C D}{O D}\)
tan α = \(\frac{C D}{O A+A D}\) ………… (4)
In the triangle CAD, sin θ = \(\frac{C D}{A C}\)
CD = AC sin θ
CD = Q sin θ ………… (5)
∴ tan α = \(\frac{\mathrm{Q} \sin \theta}{\mathrm{P}+\mathrm{Q} \cos \theta}\) (∵ AD = Q cosθ)
α = tan^-1(latex]\frac{\mathrm{Q} \sin \theta}{\mathrm{P}+\mathrm{Q} \cos \theta}[/latex]) ………. (6)

Question 13.
State the laws of rolling friction.
Answer:
Laws of friction – rolling friction :

1. The smaller the area of contact, the lesser will be the rolling friction.
2. The larger the radius of the rolling body, the lesser will be the rolling friction.
3. The rolling friction is directly propostional to the normal reaction.
   If rolling friction and ‘N’ is the normal reaction at the contact, then F_R ∞ N
   FR = μ_RN; where μ_R is the coefficient of rolling friction.

Question 14.
Find the scalar and vector products of two vectors
\(\vec{a}\) = (3î – 4ĵ + 5k̂) and \(\vec{b}\) = (- 2î – ĵ + 5k̂)
Solution:
a.b = (3\(\vec{i}\) – 4\(\vec{j}\) + 5\(\vec{k}\)).(-2\(\vec{i}\) + \(\vec{j}\) – 3\(\vec{k}\))
= – 6 – 4 – 15 = – 25

Note b × a = 7\(\vec{i}\) – \(\vec{j}\) – 5\(\vec{k}\)

Question 15.
Define the angular acceleration and torque. Establish the relation between angular acceleration and torque.
Answer:

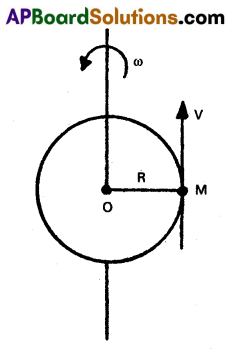
Angular acceleration :
The rate of change of angular velocity is called angular acceleration
i.e., α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\)
Torque : The rate of change of angular momentum is called torque.
Relation between angular acceleration and Torque : Consider a rigid body of mass ‘M’ rotating in a circular path of radius ‘R1 with angular velocity ‘ωω’ about fixed axis.
By definition, τ = \(\frac{\mathrm{dL}}{\mathrm{dt}}\) = \(\frac{\mathrm{d}(\omega)}{\mathrm{dt}}\)
Where I = MR² = moment of inertia of a body
τ = I\(\frac{\mathrm{d} \omega}{\mathrm{dt}}\)(∵ I = constant)
But \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\) = ∞ ∴ t = Iα

Question 16.
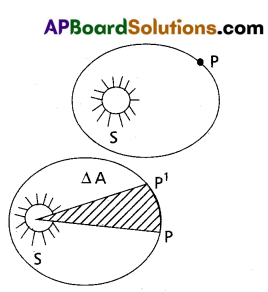
State Kepler’s laws of planetary motion.

The three laws of Kepler can be stated as follows.
1. Law of orbits : AIL planets move in elliptical orbitals with the sun situated at one of the foci.
2. Law of areas : The line that joins any planet to the sun sweeps equal areas in equal intervals of time.
3. Law of periods : The square of the time period of revolution of a planet is proportional to the cube of the semi-major axis of the ellipse traced out by the planet.
T² α R³

Question 17.
Describe the behaviour of a wire under gradually increasing load.
Answer:
When the load is increased in steps, a graph is drawn between stress on y-axis and corresponding strain on x-axis.

• Proportionality limit : In the linear position OA, stress is proportional to strain, i.e., Hookes law is obeyed by the wire upto point A. The graph is a straight line. Whenever the stretching force at A is removed, the wire regains its original length.
  A is called proportionality limit.
• Elastic limit: In the graph B is the elastic limit. Through the wire doesnot obey Hooke’s law at B. The wire regains its original length after removing the stretching force at B. upto point B the wire is under elastic behaviour.
• Permanent set (or) yield point: In the graph c is the yield point. If the stretching force at c is removed, the wire doesnot regain its original length and the length of the wire changes permanently. In this position the wire flows like a viscous liquid. After the point c, the wire is under plastic behaviour, c is called permanent set (or) yield point.
• Breaking point: When the stress increased, the wire becomes thinner and thinner. When the stress increases to a certain limit the wire breaks. The stress at which the wire breaks is called breaking stress and the point D is called breaking point.
• Elastic fatigue : The state of temporary loss of elastic nature of a body due to continuous strain is called elastic fatigue. When a body is subjected to continuous strain within the elastic limit, it appears to have lost elastic property temporarily to some extent and becomes weak.

Question 18.
Explain conduction, convection and radiation with examples. Ans. The heat is transmitted in three types. They are
1) Conduction
2) Convection
3) Radiation.

1) Conduction : The process of transmission of heat from one place to other without actual movement of the particles of the medium is called conduction.

2) Convection : The process of transmission of heat from one place to another by the actual movement of the particles is called convection.
Ex. : If water in a beaker is heated, the particles of water at the bottom receive the heat first. These particles expand, become lighter and rise up. At the same time colder and denser particles reach the bottom. They get in their turn heated and move up. This process is known as convection.

3) Radiation : The process of transmission of heat from one place to another without any intervening medium is called radiation.
Ex. : Earth receives heat radiations from the sun.

Section – C (2 × 8 = 16)

Note :

• Answer ANY TWO questions.
• Each question carries EIGHT marks.
• ALL are long answer type questions.

Question 19.
State and prove law of conservation of energy incase of a freely falling body.
A pump is required to lift 600 kg of water per minute from a well of 25 m deep and to eject it with a speed of 50 ms^-1. Calculate the power required to perform the above task.
Answer:
a) Statement: “Energy can neither be created nor destroyed. But it can be converted from one form to another form. The total energy of a closed system always remains constant”. This law is called law of conservation of energy.

Proof : Incase of freely falling body : A body of mass’m’ is dropped or freely falling at a height ‘IT from the ground. The total mechanical energy of the body E = K + U.
Where k = kinetic energy; U = potential energy.
Suppose A, B and C are the points at heights H, h and ground respectively.

At ‘A’ : At the highest point, velocity u = 0
Kinetic energy K.E = \(\frac{1}{2}\) mu² = 0
Potential energy P.E. = mgH
Total mechanical energy of the body = E_A = P.E + K.E = mgH + 0
∴ E_A = mgH ……………. (1)

At ‘B‘: When the body falls from A to B, which is at a height ‘h’ from the ground. The velocity of the body at ‘B’ is V_B.
At ‘B’ the body possesses both P.E and K.E
S = H – h
u = 0
a = g
v = v_B = ?
\(v_{\mathrm{B}}^2\) – u² = 2as
a = g \(v_{\mathrm{B}}^2\) – 0 = 2g(H – h)
v = v_B = ? v_B = 2g(H – h)

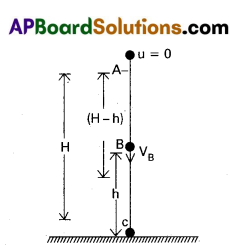
Kinetic energy of the body (K) = \(\frac{1}{2}\)\(m v_B^2\) = ^ \(\frac{1}{2}\)m2g(H – h)
K = mg (H – h) ,
v = vB = ?
Potential energy (u) = mgh
∴ Total mechanical energy at B = k + u
E_B = mg(H – h) + mgH
E_B = mgH ………… (2)

At ‘C’ : When the body reaches the point ‘c’ bn the ground. The velocity of the body at ‘c’ is ‘v_c‘ can be found by using v₂ – u₂ = 2as equation.
S = H \(v_{\mathrm{c}}^2\) – 0 = 2gH
u = 0 \(v_{\mathrm{c}}^2\) = 2gH
a = g v_c = \(\sqrt{2 \mathrm{gH}}\)
Kinetic energy of the body (k) = \(\frac{1}{2} m v_c^2\) = \(\frac{1}{2}\) m 2gH = mgH
Potential energy (u) = 0
Total energy at c = k + u
∴ E_c = mgH
From the above three equations (1), (2) and (3), the mechanical energy of the body remains constant under the action of gravitational force. Hence, law of conservation of energy is proved incase of freely falling body,

b) Here m = 600 kg; h = 25m; V = 50ms^-1;
t = 60s; power of the motor,
P = \(\frac{\mathrm{mgh}+\frac{1}{2} \mathrm{mv}^2}{\mathrm{t}}\) = \(\frac{m\left(g h \frac{v^2}{2}\right)}{t}\)
= \(\frac{600}{60}\) (9.8 25 + \(\frac{50 \times 50}{2}\))
= 10(245 + 1250) = 14950 = 14.95 KW.

Question 20.
Show that the motion of a simple pendulum is simple har¬monic and hence derive an equation for its time period. What is the length of a simple pendulum, which ticks seconds ?
Answer:

• Consider simple pendulum, a small bob of mass m tied to an inextensible mass less string of length L and other end of the string is fixed from a rigid support.
• Once, the bob is slightly displaced and released, it begins to oscillate about mean position.
• Let θ be the angular displacement and T be the tension in the string.
• The forces acting on the bob are
  (a) tension T along the string
  (b) weight mg acts vertically downwards.
• The force mg can be resolved into two components
  1. mg cos θ along the PA and
  2. mg sin θ arts along PB.
• From figure at point P,
  T = mg cos θ ……….. (1)
• The force mg sin θ will provide the restoring torque, which tends to bring the bob back to its mean position O.
• The restoring torque given by
  τ = Restoring force × ⊥^lar distance
  τ = – mg sin θ × L ………… (2)

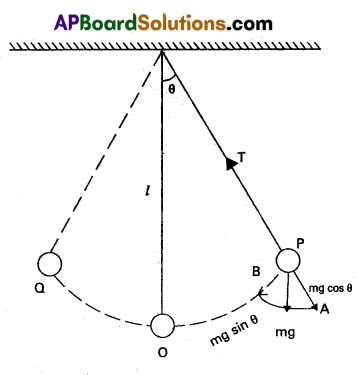
Here, negative sign shows that the torque acts to reduce θ.
Then sin θ is replaced by θ i.e., sin θ = θ
τ = -mg Lθ …… (3)
(∵ sin θ = θ – \(\frac{\theta^3}{3 !}\) + \(\frac{\theta^5}{5 !}\) …… )

• From equation (3), we note that τ ∝ θ and this τ will bring the bob back towards its equilibrium position.
  So, if the bob is left free, it will execute angular simple harmonic motion.
  Comparing equation (3), with the equation τ = -kθ, we have spring factor, k = mgL.
• Here inertia factor = Moment of inertia of the bob about the point of suspension = mL².
• In S.H.M, Time period (T) = 2π\(\sqrt{\frac{\text { Inertia factor }}{\text { Spring factor }}}\)
  T = 2π\(\sqrt{\frac{\mathrm{mL}^2}{\mathrm{mgL}}}\) ……. (4)
  T = 2π\(\sqrt{\frac{L}{g}}\)
  Seconds pendulum : A pendulum whose’time period is 2 seconds is called seconds pendulum.
  T = 2 seconds.

Question 21.
State second law of thermodynamics. How is heat engine different from a refrigerator.
Answer:
Second law of thermodynamics gives the direction of flow of heat. Second law consists two statements.
1) Kelvin – Plank statement : “No process is possible whose sole result is the absorption of heat from a reservoir and the complete conversion of the heat into work”.
(or)
It is impossible to derive a continuous supply of engine is cooling a body below the coldest of its surounding.

2) Clausius statement: “No process is possible whose sole result is the transfer of heat from a colder object to a hotter object”.
(or)
Heat can not itself flow from cold body to hot body”.

Heat engine : A device which converts heat energy into work is called heat engine.
A heat engine consists of the essential parts.

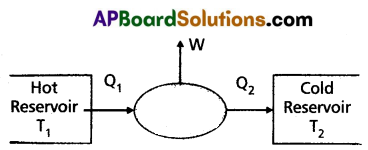
1) Source or hot reservoir : It is maintained at a very high temperature T₁. Heat is extracted from this body.
2) Working substance : In a steam engine working substance is steam. In diesel engine working substance is mixture of fuel vapour and air.
3) Sink or cold reservoir : It is maintained at a very low temperature T₂. It absorbs heat energy, rejected by working substance.

Work done : The difference of heat absorbed from source and heat rejected to sink is equal to work done by the engine, i.e., W = Q₁ – Q₂.

Efficiency : The ratio of workdone (W) by the engine to the amount of heat absorbed (Q,) by the engine is called efficiency.
i.e., η = \(\frac{\mathrm{W}}{\mathrm{Q}_1}=\frac{\mathrm{Q}_1-\mathrm{Q}_2}{\mathrm{Q}_1}\) = 1 – \(\frac{\mathrm{Q}_2}{\mathrm{Q}_1}\)

Refrigerator : Refrigerator is a heat pump which is the reverse of a heat engine.

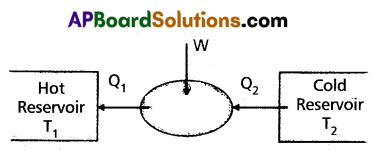
In refrigerator the working substance extracts (Q₂) an amount of heat from sink of lower temperature and a external work W is done on the working substance and finally amount of heat (Q₁) is transferred to source.
The coefficient of performance (α) of a refrigerator is given by
α = \(\frac{Q_2}{W}=\frac{Q_2}{Q_1-Q_2}\) (∵ heat released Q₁ = Q₂)
For heat engine η can never exceed 1. For refregirator a can be greater than 1.
Therefore,working of refrigerator is opposite to that of heat engine.