TS Inter 1st Year Maths 1B Question Paper May 2022

Access to a variety of TS Inter 1st Year Maths 1B Model Papers and TS Inter 1st Year Maths 1B Question Paper May 2022 allows students to familiarize themselves with different question patterns.

TS Inter 1st Year Maths 1B Question Paper May 2022

Time : 3 Hours
Max. Marks : 75

Note : This question paper consists of THREE sections A, B and C.

Section – A
(10 × 2 = 20 Marks)

I. Very short answer type questions :

1. Answer all the questions.
2. Each question carries two marks.

1. Find the equation of the line containing the points (2, -3) and (0, -3).

2. Transform the equation 3x + 4y = 5 into intercept form. Find the length of the perpendicular from (-2, -3) to the straight line 5x – 2y + 4 = 0.

3. Find the length of the perpendicular from (-2, -3) to the straight line 5x – 2y + 4 = 0

4. Find the ratio in which the X-axis divide the line segment \(\overline{\mathrm{AB}}\) joining A(2, -3) and B(3, -6).

5. Show that the points A (3, -2, 4), B (1, 1, 1) and C (-1, 4, -2) are collinear.

6. Find x if the distance between (5, -1, 7) and (x, 5, 1) is 9 units.

7. Find the ratio in which the XZ-plane divides the line joining A (-2, 3, 4) and B (1, 2, 3).

8. Find the direction cosines of the normal to the plane x + 2y + 2z – 4 = 0.

9. Find

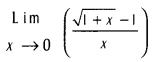
10. Show that

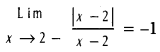
11. Find

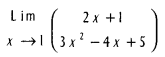
12. Find the derivative of f (x) = e^x. (x² + 1)

13. If y = Log (S in (L og x )), then find \(\frac{d y}{d x}\).

14. Find ∆y and dy for the function y = x² + 3x + 6, x = 10 and ∆x = 0.01.

15. Find the slope of the tangent to the curve y = 3x⁴ – 4x at x = 4.

Section – B
(5 × 4 = 20)

II. Short Answer Type Questions.

1. Answer any FIVE questions.
2. Each Question carries FOUR marks.

16. Find the locus of the third vertex of a right angled triangle, the ends of whose hypotenuse are (4, 0) and (0, 4).

17. A(5, -3), B(3, -2) are two fixed points. Find the equation of the locus of P, so that the area of triangle PAB is 9.

18. Find the equation of locus of a point which is equidistant from the points A(3, -2) and B(0, 4).

19. When the origin is shifted to (-1, 2) by the translation of axes, find the transformed equation of x² + y² + 2x – 4y + 1 = 0.

20. When the axes are rotated through an angle π/6, find the transformed equation of x² + \(2 \sqrt{3}\)xy – y² = 2a².

21. Find the value of F if the lines 3x + 4y = 5, 2x + 3y = 4, Px + 4y = 6 are concurrent.

22. Find the foot of the perpendicular drawn from (4, 1), upon the straight line 3x – 4y + 12 = 0.

23. Find the coordinates of the vertex C of ∆ABC if its centroid is the origin and the vertices A, B are (1, 1, 1) and (-2, 4, 1) respectively.

24. Compute \(\lim _{x \rightarrow \infty} \frac{x^2+5 x+2}{2 x^2-5 x+1}\)

25. Find the derivative of the function Cos ax from the first principles.

26. Find the equation of tangent and normal to the curve xy = 10 at (2, 5)

27. Find two positive integers whose sum is 16 and the sum of whose squares is minimum.

Section – C

III. Long Answer Type Questions.

1. Answer ANY FIVE questions.
2. Each Question carries SEVEN marks.

28. Find the circumcenter of the triangle whose vertices are (1, 0), (-1, 2) and (3, 2).

29. Find the orthocenter of the triangle whose vertices are (-2, -1), (6, -1) and (2, 5).

30. Find the equation of the straight line passing through (1, 3) and

i) Parallel to
ii) Perpendicular to the line passing through the points (3, – 5) and (-6, 1).

31. Show that the product of the perpendicular distances from a point (α, β) to the pair of straight lines \(\frac{\left|a \alpha^2+2 h \alpha \beta+b \beta^2\right|}{\sqrt{(a-b)^2+4 h^2}}\)

32. Find the condition for the chord lx + my = 1 of the circle x² + y² = a² (whose center is the origin) to subtend a right angle at the origin.

33. Find the angle between two diagonals of a cube.

34. Find the derivatives of the functions:

i) Log (Tan 5x)
ii) Tan (e^x)

35. Find the derivative of

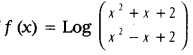
36. Find the derivatives of the functions:

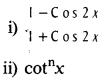
37. Find the angle between the curves y² = 4x, x² + y² = 5.