TS Inter 1st Year Maths 1B Question Paper May 2018

Access to a variety of TS Inter 1st Year Maths 1B Model Papers and TS Inter 1st Year Maths 1B Question Paper May 2018 allows students to familiarize themselves with different question patterns.

TS Inter 1st Year Maths 1B Question Paper May 2018

Time : 3 Hours
Max. Marks : 75

Note : This question paper consists of THREE sections A, B and C.

Section – A
(10 × 2 = 20 Marks)

I. Very short answer type questions :

1. Answer all the questions.
2. Each question carries two marks.

Question 1.
Find the equation of the straight line passing through (-4, 5) and cutting off equal and non-zero intercepts on the co-ordinate axes.
Solution:
Let x – intercept = a
y – intercept = a
Intercept form : \(\frac{x}{a}+\frac{y}{a}\) = 1
⇒ x + y = a
If this straight line passing through (-4, 5) then -4 + 5 = a
⇒ a = 1
∴ Required straight line equation is x + y = 1
⇒ x + y – 1 = 0

Question 2.
Find the distance between the parallel lines 5x – 3y – 4 = 0, 10x – 6y – 9 = 0.
Solution:
Given line equations are
(5x – 3y – 4 = 0) × 2 ⇒ 10x – 6y – 8 = 0 ……. (1)
10x – 6y – 9 = 0 …………………… (2)
The distance between the parallel lines (1) and (2) = \(\frac{\left|c_2-c_1\right|}{\sqrt{a^2+b^2}}\)
= \(\frac{|-9+8|}{\sqrt{10^2+6^2}}\)
= \(\frac{1}{\sqrt{136}}\)

Question 3.
Find the co-ordinates of the vertex C of ∆ABC, if its centroid is the origin and the vertices A, B are (1, 1, 1) and (-2, 4, 1) respectively.
Solution:
Given A = (1, 1, 1)
B = (-2, 4, 1)
Let C = (x, y, z)
Since origin is the centroid of ∆ABC.

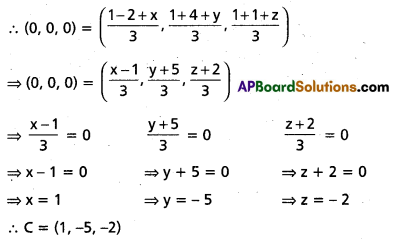
Question 4.
Find the intercepts of the plane 4x + 3y – 2z + 2 = 0 on the co-ordinate axes.
Solution:
Given plane equation is 4x + 3y – 2z + 2 = 0.
⇒ 4x + 3y – 2z = – 2

∴ X – intercept = \(\frac{-1}{2}\)
y — intercept = \(\frac{-2}{3}\)
z — intercept = 1

Question 5.
Compute

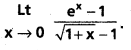
Solution:

Question 6.
Evaluate

Solution:

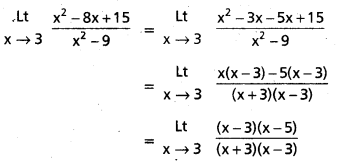
Question 7.
If f(x) = xe^x sin x then find f (x).
Solution:

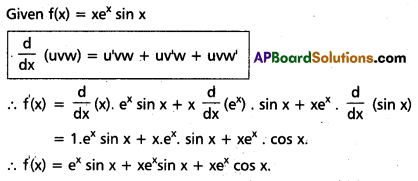
Question 8.
If y = \(e^{a \sin ^{-1} x}\) then prove that \(\frac{d y}{d x}\) = \(\frac{a y}{\sqrt{1-x^2}}\).
Solution:

Question 9.
If the increase in the side of a square is 4% then find the approximate percentage of increase in the area of the square.
Solution:
Let x, A be the side, area of a square respectively.
Given \(\frac{\delta x}{x}\) × 100 = 4.
A = x²
δA = 2x δx
\(\frac{\delta A}{A}\) × 100 = \(\frac{2 x \delta x}{x^2}\) × 100
= 2.\(\frac{\delta x}{x}\) × 100
= 2.4
= 8.
∴ The approximate percentage of increase in the area of the square is 8.

Question 10.
Define Lagrange’s mean value theorem.
Solution:
Lagrange’s mean value theorem:
Let a, b ∈ R (a < b). If f : [a, b] → R be a function Such that

(i) f is continuous on [a, b] and
(ii) f is derivable on (a, b) then there exists

c ∈ (a, b) such that f'(c) = \(\frac{f(b)-f(a)}{b-a}\)

Section – B

II. Short Answer Type Questions. (5 × 4 = 20)

1. Attempt any five questions.
2. Each question carries four marks.

Question 11.
Find the equation of the locus of a point, the difference of whose distances from (-5, 0) and (5, 0) is 8.
Solution:
A(5, 0), B(-5, 0) are the given points.

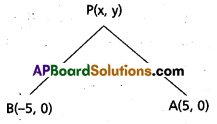
P(x, y) is any point on the locus.
Given condition is [PA – PB] = 8
PA – PB = 8
PA² – PB² = [(x – 5)² + (y – 0)²] – [(x + 5)² + (y – 0)²] ……… (1)
= x² – 10x + 25 + y² – x² – 10x – 25 – y²
= – 20x
(PA + PB) (PA – PB) = -20x
(PA + PB) 8 = – 20x
(PA + PB) = – \(\frac{5}{2}\)x
Adding (1) and (2),
2PA = \(\frac{5 x}{2}\) + 8 = \(\frac{-5 x+16}{2}\)
4PA = – 5x + 16
16PA² = (-5x + 16)²
16 [x – 5)² + y²] = (-5x + 16)²
16 [x² – 10x + 25 + y²] = [-5x + 16]²
16x² + 16y² – 160x + 400 = 25x² + 256 – 160x
9x² – 16y² = 144
Dividing with 144, locus of P is
\(\frac{9 x^2}{144}-\frac{16 y^2}{144}\) = 1 i.e., \(\frac{x^2}{16}-\frac{y^2}{9}\) = 1

Question 12.
When the axes are rotated through an angle 45°, the transformed equation of a curve is 17x² – 16xy + 17y² = 225. Find the original equation of the curve.
Solution:

Question 13.
A straight line through P(3, 4) makes an angle of 60° with the positive direction of the X – axis. Find the co-ordinates of the points on the line which are 5 units away from P.”
Solution:
Given P = (3, 4) at θ = 60°
The co-ordinates of the points on the line which are 5 units away from P is (x₁ ± r cos θ, y₁ ± r sin θ)
= (3 ± 5 cos 60°, 4 + 5 sin 60°)
= \(\left(3 \pm 5\left(\frac{1}{2}\right), 4 \pm 5 \cdot \frac{\sqrt{3}}{2}\right)\)

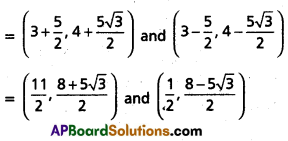
Question 14.
If f, given by

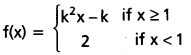
is a continuous function on R, then find the values of k.
Solution:
Given

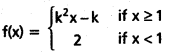
Since f is a continuous function on R

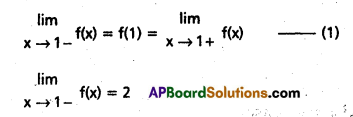
Also f(1) = k²(1) – k = k² – k
From (1)
k² – k = 2
⇒ k² – k – 2 =0
⇒ k² – 2k + k – 2 = 0
⇒ k(k – 2) + 1 (k – 2) = 0
∴ k = 2 (or) k = -1

Question 15.
Find the derivative of the function cos (ax) from the first principle.
Solution:
Let f(x) = cos (ax)
f(x + h) = cos a (x + h) ⇒ cos (ax + ah)

Question 16.
Find the equation of tangent and normal to the curve xy = 10 at (2, 5).
Solution:
Given curve equation is xy = 10
differentiate w.r.to ‘x’ on both sides, we get

Question 17.
The volume of a cube is increasing at the rate of 8 cm³/sec. How fast is the surface area increasing, when the length of an edge is 12 cm?
Solution:
Let x, v, s be length of an angle edge, volume and surface area of the cube respectively.
Given x = 12 cm.
\(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 8 cm³/sec.
We know v = x³
\(\frac{\mathrm{dv}}{\mathrm{dt}}\) = \(3 x^2 \frac{d x}{d t}\)
\(\frac{d x}{d t}\) = \(\frac{1}{3 x^2} \frac{d v}{d t}\)
∴ Surface area increasing at the rate of \(\frac{8}{3}\) cm²/sec

Section – C

III. Long Answer Type Questions. (5 × 7 = 35)

1. Attempt any five questions.
2. Each question carries seven marks.

Question 18.
Find the circumcentre of the triangle whose vertices are (1, 3), (0, -2) and (-3, 1).
Solution:
Let A = (1, 3)
B = (0, -2)
C = (-3, 1)
Let S (α, β) be the circumcentre of the triangle ABC.

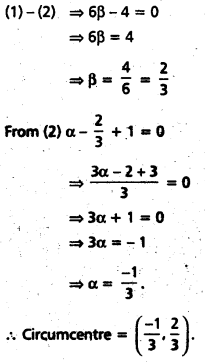
Question 19.
Show that the product of the perpendicular distance from a point (α, β) to the pair of straight lines ax² + 2hxy + by² = 0 is

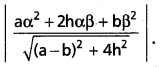
Solution:
let ax² + 2hxy + by² ≡ (l₁x + m₁y) (l₂x + m₂y)
Then the separate equations of the lines represented by the equation
ax² + 2hxy + by² = 0 are
L₁ : l₁x + m₁y = 0 and L₂ : l₁x + m₂y = 0
Also, we have l₁l₂ = a; m₁m₂ = b and
l₁m₂ + l₂m₁ = 2h
d₁ = length of the perpendicular

Question 20.
Find the angle between the lines joining the origin to the points of intersection of the curve x² + 2xy + y² + 2x + 2y – 5 = 0 and the line 3x – y + 1 = 0.
Solution:

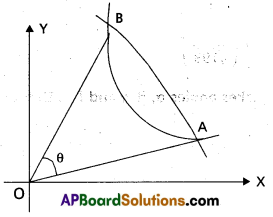
Equation of the curve is
x² + 2xy + y² + 2x + 2y – 5 = 0 …….. (1)
Equation of AB is 3x – y + 1 = 0
y – 3x = 1 ……. (2)
Homogenising (1) with the help of (2), combined equatio of OA, OB is
x² + 2xy + y² + 2x.1 + 2y.1 – 5.1² = 0
x² + 2xy + y² + 2x (y – 3x) + 2y (y – 3x) – 5 (y – 3x)² = 0
x² + 2xy + y² + 2xy – 6x² + 2y² – 6xy – 5(y² + 9x² – 6xy) = 0
-5x² – 2xy + 3y² – 5y² – 45x² + 30 xy = 0
-50x² + 28xy – 2y² = 0
i.e., 25x² – 14xy + y² = 0
Suppose θ is the angle between OA and OB

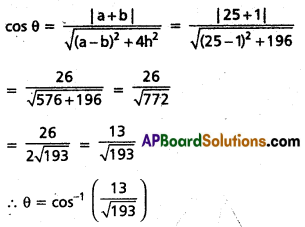
Question 21.
If a ray makes angles α, β and γ with four diagonals of a cube, then find cos²α + cos²β + cos²γ + cos²δ.
Solution:
Let each side of the cube be of length a. Let one of the vertices of the cube be the origin O and the co-ordinate axes be along the three edges \(\overline{\mathrm{OA}}\), \(\overline{\mathrm{OB}}\) and \(\overline{\mathrm{OC}}\) passing through the origin. The co-ordinates of the vertices of the cube with respect to the frame of reference OABC are as shown in figure. The diagonals of he cube are \(\overline{\mathrm{OP}}\), \(\overline{\mathrm{CD}}\), \(\overline{\mathrm{AE}}\) and \(\overline{\mathrm{BF}}\). (a, a, a), (a, a, -a), (-a, a, a) and (a, -a, a) are direction ratios of these diagonals respectively.

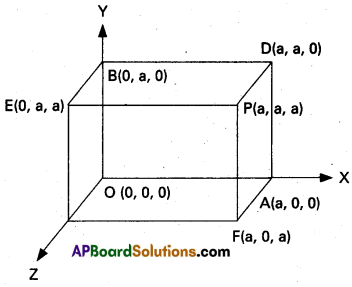
Let the direction cosines of the given ray be (l, m, n): If this ray makes the angles α, β, γ and δ with the four diagonals of the cube, then

Question 22.
If y = tan^-1\(\left[\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\right]\) for 0 < |x| < 1, find \(\frac{d y}{d x}\).
Solution:

Question 23.
If the tangent at any point P on the curve x^m.yⁿ = a^m+n (mn ≠ 0) meets the co-ordinate axes in A, B, then show that AP : BP is a constant.
Solution:
Given curve equation is x^m. yⁿ = a^m+n
Taking logarithms on both sides, we have
log x^m. yⁿ = log a^m+n
⇒ log x^m + log yⁿ = (m + n) log a
⇒ m log x + n log y = (m + n) log a ……… (1)
Let P (x₁, y₁) be any point on the curve.
Differentiating (1) w.r.to ‘x’ on both sides, we have

Since the tangent meets the co-ordinate axes at A, B.

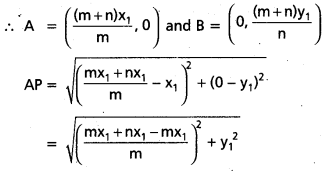
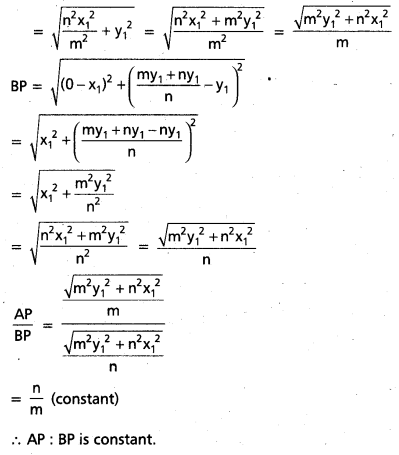
Question 24.
A wire of length λ is cut into two parts which are bent respectively in the form of a square and a circle. What are the lengths of the pieces of the wire respectively, so that the sum of the areas is the least ?
Solution:
Suppose x is the side of the square and r is the radius of the circle
Given 4x + 2πr = l
4x = l – 2πr
x = \(\frac{l-2 \pi r}{4}\)
Sum of the area = x² + nπ²


∴ f(r) is least when r = \(\frac{l}{2(\pi+4)}\)
Sum of the area is least when the wire is cut into pieces of length
\(\frac{\pi l}{\pi+4}\) and \(\frac{4 l}{\pi+4}\)