TS Inter 1st Year Physics Question Paper March 2019

Thoroughly analyzing TS Inter 1st Year Physics Model Papers and TS Inter 1st Year Physics Question Paper March 2019 helps students identify their strengths and weaknesses.

TS Inter 1st Year Physics Question Paper March 2019

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note:

• Answer all questions.
• Each question carries two marks.
• All are very short answer type questions.

Question 1.
What is the contribution of S. Chandrasekhar to Physics ?
Answer:
While studying the constitution of the stars, he has proved that the maximum mass that a white dwarf can have is 1.4 times the solar mass. This mass is known as Chandrasekhar limit. If a star crosses this limit, it has to face a catostropic collapse.

Question 2.
Define unified atomic mass unit and write its value in kg.
Answer:
1 unified atomic mass unit
= \(\frac{1}{2}\) of the mass of carbon – 12 atom.
1 a.m.u = 1.66 × 10^-27 kg.

Question 3.
What is the acceleration of the projectile at the top of its trajectory ?
Answer:
The acceleration of a projectile at the top of its trajectory is vertically downwards.

Question 4.
What happens to coefficient of friction if the weight of the body is doubled ?
Answer:
If weight of a body is doubled, coefficient of friction does not change. Coefficient of friction independent of normal reaction. If weight is’ doubled, normal reaction doubled and corresponding frictional force doubled. So, coefficient of friction does not change.

Question 5.
What is Magnus effect ?
Answer:
The difference in the velocity of air results in the pressure difference between the lower and upper faces and there is a net upwards force on the ball. This dynamic lift due to spinning is called magnus effects.

Question 6.
What is meant by hydrostatic paradox ?
Answer:
Consider three vessels A, B and C of different shapes. They are connected at the bottom by a horizontal pipe. On filling with the level in the three vessels is the same, through they hold different amount of water. This is so because water at the bottom has the same pressure below each section of the vessel. It means the liquid pressure at a point is independent of the quantity of liquid but depends upon the depth of point below the liquid surface. This is known as hydrostatic paradox.

Question 7.
If the maximum intensity of radiation for a black body is found at 1.45 μm, what is the temperature of radiating body ? (Wien’s constant = 2.9 × 10^-3 mk).
λ_max = 1.45 μm
= 1.4 5 × 10^-6 m.
Wien’s constant (b) = 2.9 × 10^-3 mk
λ_max T = b
⇒ T = \(\frac{\mathrm{b}}{\lambda_{\max }}\) = \(\frac{2.9 \times 10^{-3}}{1.45 \times 10^{-6}}\) = 2 × 10³ k.

Question 8.
Why do liquids have no linear and areal expansions ?
Answer:
Liquids occupy the same shape of vessel. They do not have individual length and area. Hence, liquids have no linear and areal expansions.

Question 9.
When does real gas behave like an ideal gas ?
Answer:
At low pressures and high temperatures real gases behave like an ideal gas.

Question 10.
The absolute temperature of gas is increased by 3 times. What will be the increase in rms velocity of the gas molecule ?
Answer:
case (i) : The r.m.s velocity of gas molecule, \(\overline{v_1}=\sqrt{\frac{3 R T_1}{M}}\)

case (ii) : The r.m.s velocity of gas molecule, \(\overline{v_2}=\sqrt{\frac{3 R T_2}{M}}\)
\(\frac{\overline{v_2}}{\overline{v_1}}\) = \(\sqrt{\frac{T_2}{T_1}}\) = \(\sqrt{\frac{3 \mathrm{~T}_1}{\mathrm{~T}_1}}\) [∵ T₂ = 3T₁]
⇒ \(\overline{v_2}\) = 3\(\overline{v_1}\) = 1.732 \(\overline{v_1}\)
∴ Increases in r.m.s velocity of gas molecule
= \(\overline{v_2}\) – \(\overline{v_1}\) = 1.732 \(\overline{v_1}\) – \(\overline{v_1}\) = 0.732 \(\overline{v_1}\).

Section – B (6 × 4 = 24)

Note:

• Answer any six questions.
• Each question carries four marks.
• All are Short Answer type Questions.

Question 11.
Derive the equation, S = ut + 1/2 at² from υ-t graph.
Answer:
Let a body moves along a straight line with initial velocity ‘u’ and uniform acceleration ‘a’.

It attains the velocity ‘v’ in the time ‘t’ after the displacement ‘s’. Its velocity time graph is shown in figure.

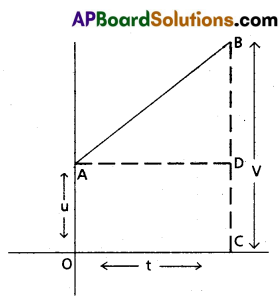
From the diagram, OC = AD = t.
OA = CD = u
BD = BC – CD = V – u.
displacement, S = Area of rectangle ADCO + area of Δ ABD
⇒ S = (OC) (OA) + \(\frac{1}{2}\) (AD) (BD)
⇒ S = (t) (u) + \(\frac{1}{2}\) (t) (v – u)
⇒ S = ut + \(\frac{1}{2}\) (t)(at) [∵ v = u + at]
⇒ S = ut + \(\frac{1}{2}\) at²

Question 12.
0 is the point on the ground chosen as origin. A body first suffers a displacement of 10√2 m North-East, next 10m North and finally 10√2 m North-West. How far is it from the origin ?
Answer:
Given OB = 10√2 m, BC = 10m
OB = \(\sqrt{O A^2+A B^2}\) (∵ OA = 10\(\vec{i}\) AB + 10\(\vec{j}\))
OB = \(\sqrt{10^2+10^2}\) = 10√2 m

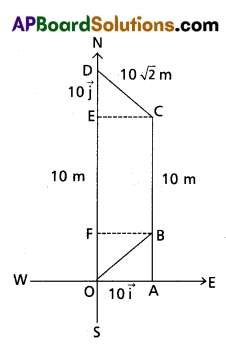
Similarly EC = 10\(\vec{i}\) , ED = 10\(\vec{j}\)
∴ CD = \(\sqrt{10^2+10^2}\)
CD = 10√2 m
Total displacement (OD) = |OF| + |FE| + |ED|
OD = 10 + 10 + 10
OD = 30 m.

Question 13.
Explain the various methods to minimise the friction ?
Answer:

• Polishing : By polishing the surfaces of contact, friction can be reduced.
• Bearings : The rolling friction is less than the sliding friction hence free wheels of a cycle, motocar, dynamos etc., are provided with ball bearing to reduce friction. Bearings convert sliding motion into rolling motion.
• Lubricants: The lubricants forms a thin layer between surfaces of contact. It reduces the friction in light vehicles or machines, oils like “three in one” are used as lubricants. In heavy machines grasure is used. In addition to this they guand the aeroplanes parts from over heating.
• Streamlining: Automobiles and aeroplanes are stream-linined to reduce the friction due to air.

Question 14.
What is the moment of inertia of a rod of mass M and length L about an axis perpendicular to it and passing through one end ?
Answer:
For the rod of mass M and length l, I = Ml²/12.
using the parallel axes theorem, I = I + Ma²
with a = l/2 we get,
I = M\(\frac{l^2}{12}\) + M(\(\frac{l}{2}\))² = \(\frac{M l^2}{3}\)
We can check this independently since I in half the moment of inertia of a rod of mass 2M and length 21 about its midpoint.
I¹ = 2M \(\frac{4 l^2}{12}\) × \(\frac{1}{2}\) = \(\frac{M l^2}{3}\)

Question 15.
Define vector produce of two vectors and write any two properties of it ?
Answer:
The cross product of two vectors is given by \(\vec{C}\) = \(\vec{A}\) × \(\vec{B}\) . The magnitude of the vector defined from cross product of two vectors is equal to product of magnitudes of the vectors and sine of angle between the vectors.

Direction of the vectors is given by right hand corkscrew rule and is perpendicular to the plane containing the vectors.
∴ | \(\vec{C}\) | = AB sin θ. and \(\vec{C}\) = AB sin θ n̂where,
n̂ is the unit vector perpendicular to the plane containing the vectors \(\vec{A}\) and \(\vec{B}\)

Example :
1) Torque is cross product of position vector and Force.
i.e., \(\vec{T}\) = \(\vec{r}\) × \(\vec{F}\)

2) Angular momentum is cross product of position vector and momentum
i.e., \(\vec{L}\) = \(\vec{r}\) × \(\vec{P}\)

Properties :
1) Cross product does not obey commutative law. But its magnitude obey’s commutative law.
\(\vec{A}\) × \(\vec{B}\) ≠ \(\vec{B}\) × \(\vec{A}\) = (\(\vec{A}\) × \(\vec{B}\)) = – (\(\vec{B}\) × \(\vec{A}\)) , |(\(\vec{A}\) × \(\vec{B}\))| = |(\(\vec{B}\) × \(\vec{A}\))|

2) It obeys distributive law \(\vec{A}\) × (\(\vec{B}\) × \(\vec{C}\)) = \(\vec{A}\) × \(\vec{B}\) + \(\vec{A}\) × \(\vec{C}\)

3) The magnitude of cross product of two vectors which are parallel is zero.
Since θ = 0; | \(\vec{A}\) × \(\vec{B}\) | = AB sin 0° = 0

4) For perpendicular vectors, θ = 90°, | \(\vec{A}\) × \(\vec{B}\) | = AB sin 90° | n̂ | = AB

Question 16.
Define escape velocity and derive an expression for it.
Answer:
Escape velocity : It is the minimum velocity in a body should by projected, so that it moves into the space by overcoming the earth’s gravitational field.

Expression for escape velocity :
Consider a body of mass m thrown with a velocity Ve.
Then K.E = 1\(\frac{1}{2} m v_{\mathrm{e}}^2\)  ________ (1)
The gravitational force of attraction of the earth of mass M and Radius R on a body of mass m at its surface is
F = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) ________ (2)
Gravitational P.E. = work done on the body
∴ P.E. = F × R = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) × R
P.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\) ________ (3)
A body just escapes when its K.E. = P.E.

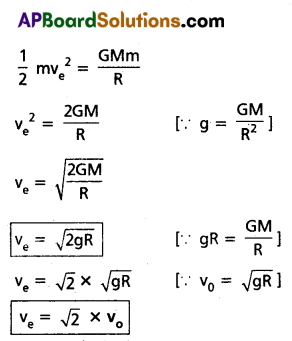
∴ Escape velocity is √2 times the orbital velocity.

Question 17.
Define strain energy and derive an expression for it.
Answer:
The potential energy stored in a body when stretched is called strain energy.
Let us consider a wire of length L and cross – sectional area A. Let X be the change in length of the wire by the application of stretching force F.
Young’s modulus = \(\frac{\text { Longitudinal Stress }}{\text { Longitudinal Strain }}\)
y = \(\frac{\mathrm{FL}}{\mathrm{Ax}}\)
F = \(\frac{y A x}{L}\) ________ (1)
To stretch the wire further by dx, the workdone dw = F.dx;
dw = F.dx
dw = (\(\frac{Y A x}{L}\))dx
Total workdone to stretch the wire from 0 to x is given by

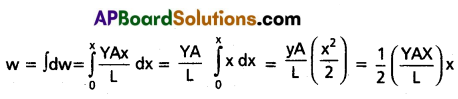
w = \(\frac{1}{2}\)F.x = \(\frac{1}{2}\) × stretching force × elongation
The work done is stored in the form of potential energy.
u = \(\frac{1}{2}\).Fx. ________ (2)
Strain energy per unit volume = \(\frac{1}{2}\) × \(\frac{F}{A}\).\(\frac{x}{L}\)
= \(\frac{1}{2}\) × stress × strain.

Question 18.
Pendulum clocks generally go fast in winter and slow in summer. Why ?
Answer:
The time period of a pendulum is given by.
T = 2π\(\sqrt{\frac{l}{g}}\)
where ‘l’ is the length of the pendulum.
Thus T α √l In summer, T will increase as l increase white in winter, T will decrease, as ‘l’ decrease. Likewise, pendulum clocks go fast in winter and slow in summer.

Section – C (2 × 8 = 16)

Note:

• Answer any two questions.
• Each question carries eight marks.
• All are Long Answer Type Questions.

Question 19.
a) State law of conservation of energy and verify in the case of freely falling body.
b) Calculate the power of a pump required to life 00 kg of water per minute from a well of 25 m deep.
Answer:
a) Statement : Energy can neither be created nor destroyed, but it can be converted from one form to another form. The total . energy a system always remains constant.

Verification in the case of freely falling body : Let a body of mass ‘m’ be at a height h above the ground. When it is freely falling with an acceleration due to gravity g, the potential energy gradually dicreases and at the same time the K.E. of the body increases.

When the body is at A:
At the highest point final velocity v = 0
Kinetic energy K.E. = \(\frac{1}{2}\) mv² = 0
Potential energy P.E. = mgh
Total energy at A = E = P.E. + K.E. = mgh + 0
∴ Total energy at A, E = mgh ……………. (1)

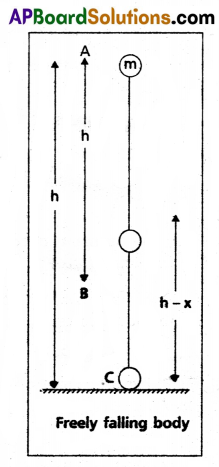
When the body is at B :
As the body falls freely, after travelling a distance x, reaches point B.
At ‘B’ the body possesses both P.E. and K.E.
Potential energy P.E. = mg(h – x)
P.E. = mgh – mgx
Kinetic energy K.E. = \(\frac{1}{2} m v_1^2\)
∴ Total energy at B = P.E. + K.E.
= mgh – mgx + \(\frac{1}{2} m v_1^2\)
For freely falling body
s = x
u = 0
v = v₁
a = g
Sub, these values in equation
v² – u² = 2as
\(v_1^2\) – 0² = 2gs
\(v_1^2\) – 0² = 2gx
\(v_1^2\) = 2gx
Total energy at
B = mgh – mgx + \(\frac{1}{2}\) m. 2gx
= mgh – mgx + mgx = mgh
∴ Total energy of BE = mgh ………. (2)

When the body is at C :
The body falls through a distance of ‘h’ and touches the ground at C with a velocity v₂.
Potential energy (P.E.) at C = mg = 0
Kinetic energy K.E. = \(\frac{1}{2} m v_2^2\)
Total energy at C = 0 + \(\frac{1}{2} m v_2^2\) = \(\frac{1}{2} m v_2^2\)
For freely falling body s = h, u = 0, v = v₂ a = g
Sub. these values in equation. v² – u² = 2as ; \(v_2^2\) – 0² = 2gh
\(v_2^2\) = 2gh
Sub this value in total energy we get
Total energy at C = \(\frac{1}{2} m v_2^2\) = \(\frac{1}{2}\) m 2gh
∴ Total energy at C E = mgh
In the above three cases total energy of the body is proved constant. Hence law of conservation of energy is proved.

Conditions : The total mechanical energy of the system remains constant, under the action of the gravitational force which is a conservatice force.

If some of the internal forces tike air resistance and friction, different parts of the system are present which are non conservative, then the total mechanical energy is not constant.

b) Here, m = 600 kg, h = 25 m, v = 50 m/s, t = 60 sec
power of moto, p = \(\frac{\mathrm{mgh}+\frac{1}{2} m v^2}{\mathrm{t}}\) = \(\frac{m\left(g h+\frac{v^2}{2}\right)}{t}\)
⇒ p = \(\frac{600}{60}\)(9.8 × 25 + \(\frac{50 \times 50}{2}\))
= 10 (245 + 1250) = 14.95 kw.

Question 20.
a) Define simple harmonic motion. Show that the motion of (point) projection of a particle performing uniform circular motion on any diameter is simple harmonic.
Answer:
“A body is said to be in simple harmonic motion, if it moves to and from along a straight line, about its mean position such that, at any point its acceleration is directly proportional to its displacement in magnitude but opposite in direction and is directed always towards the mean position”.

If ‘a’ is the acceleration of the body at any given displacement ‘y’ from the mean position, then for the body to be in S.H.M.
a ∝ – y or, a = – ky
Where ‘k’ is constant of proportionality. (-) indicates that ‘a’ and V are always in opposite directions.

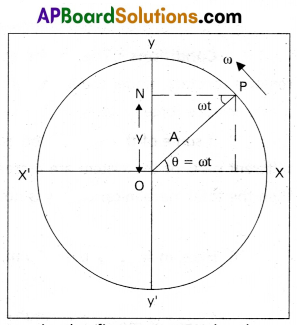
Show that the projection of uniform circular motion on any diameter is simple harmonic : Consider a particle P moving on the circumference of a circle of radius A with uniform angular velocity ω. Let O be the centre of the circle. XX’ and YY’ are two mutually perpendicular diameters of the circle as shown in the figure. Let PN be drawn perpendicular to the diameter YY’ from P. As P moves on the circumference of the circle, N moves on the diameter YY1 to and from about the centre O. Let us consider the position of N at any time t, after leaving the point ‘O’, during its motion. The corresponding angular displacement of the particle P is ∠XOP = θ = ωt.
From Δ^leONP, sin ωt = \(\frac{\mathrm{ON}}{\mathrm{OP}}\);
ON = OP sin ωt (∵ ON = y, OP = A)
y = A sin ωt ________ (1)
Differentiating equation (1) w.r.t’t’, we get velocity

Hence acceleration is directly proportional to the displacement and opposite direction. Hence motion of N is simple harmonic.

b) A mass of 2 kg is attached to a spring of force constant 200 Nm^-1. Find its time period.
Answer:
Here, mass, m = 2 kg
Force constant, k = 200 N/m
Time period, T = 2π\(\sqrt{\frac{m}{k}}\)
= 2π\(\sqrt{\frac{2}{200}}\)
= 2π\(\sqrt{\frac{1}{100}}\)
T = \(\frac{2 \pi}{10}\)
⇒ T = \(\frac{\pi}{5}\)sec

Question 21.
Explain reversible and irreversible processes. Describe the working of Carnot’s engine. Obtain an expression for the efficiency.
Answer:
Reversible process : A process that can be retraced back in the opposite direction in such away that the system passes through the same states as in the direct process, and finally the system and the surroundings return in their original states, is called a reversible process.
A reversible process is only a purely idealised process.

Examples:

1. Slow isothermal and slow adiabatic changes.
2. Peltier effect and seeback effect.
3. Fusion of ice and vaporisation of water.

Irreversible process : “A process that cannot be retraced back in the opposite direction” is called as irreversible process.
In this process the system does not pass through the same intermediate states as in the reversible process.
All natural processes such as conduction, radiation, radioactivity etc, are irreversible.

Example:

1. Work done against friction.
2. Heat produced in conductors by passing a current through it. (Joule heating)
3. Diffusion of gases.

Carnot Engine : A reversible heat engine operating Between two temperatures is called a carnot engine. The cycle operating it is known as carnot’s cycle. In this cycle the working substance(say an ideal gas) is taken through a-cycle by means of two isothermals and two adiabatics. The four operations are shown in P – V (Indicator) diagram.

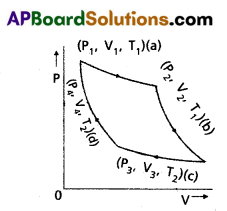
Step 1 → 2 : Isothermal expansion of the gas taking its state from (P₁, V₁, T₁) to (P₂, V₂, T₂). It is shown in curve (a).
The heat absorbed by the gas (Q₁) from the reservoir at temperature T₁ equals the workdone by the gas. i.e.
W_{1 → 2} = Q₁ = μRT₁ log_e \(\frac{V_2}{V_1}\) → (1)

Step 2 → 3 : Adiabatic expansion of the gas from (P₂, V₂, T₁) to
(P₃, V₃, T₂). It is shown in curve (b). The work done by the gas is given by
W_{2 → 3} = \(\frac{\mu R\left(T_1-T_2\right)}{(r-1)}\) → (2)

Step 3 → 4 : Isothermal compression of the gas from (P₃, V₃, T₂) to (P₄, V₄, T₂). It is shown in curve (c).
Heat released (Q₂) by the gas to the reservoir at temperature T₂ equals the work done on the goes.
i.e., W_{3 → 4} = μRT₂ log_e\(\frac{V_4}{V_3}\) = – μ RT₂ log_e\(\frac{V_3}{V_4}\)

Step _{4 → 1} : Adiabatic compression of the gas from (P₄, V₄, T₂) to (P₁, V₁, T₁). It is shown incurve (d).
W_{4 → 1} = μR \(\frac{\left(T_2-T_1\right)}{(r-1)}\) = – μR \(\frac{\left(T_1-T_2\right)}{(r-1)}\)
Total workdone by the gas in one complete cycle is
W = W_{1 → 2} + W_{2 → 3} + W_{3 → 4} + W_{4 → 1}