TS Inter 1st Year Maths 1B Question Paper March 2020

Access to a variety of TS Inter 1st Year Maths 1B Model Papers and TS Inter 1st Year Maths 1B Question Paper March 2020 allows students to familiarize themselves with different question patterns.

TS Inter 1st Year Maths 1B Question Paper March 2020

Time : 3 Hours
Max. Marks : 75

Note : This question paper consists of THREE sections A, B and C.

Section – A
(10 × 2 = 20 Marks)

I. Very short answer type questions :

1. Answer all the questions.
2. Each question carries two marks.

Question 1.
Find the value of p, if the straight lines x + p = 0, y + 2 = 0 and 3x + 2y + 5 = 0 are concurrent.
Solution:
Equations of the given lines are
x + p = 0 ….. (1)
y + 2 = 0 ….. (2)
3x + 2y + 5 = 0 …. (3)
From (2), y = – 2
Substituting in (3) 3x – 4 + 5 = 0
3x = 4 – 5 = – 1
x = –\(\frac{1}{3}\)
Point of intersection of (2) and (3) is P
The given lines are concurrent P is a point on x + p = 0
–\(\frac{1}{3}\) + p = 0 ⇒ p = \(\frac{1}{3}\)

Question 2.
Find the length of the perpendicular drawn from the point (3, 4) to the straight line 3x – 4y + 10 = 0.
Solution:
Length of the perpendicular
= \(\frac{13.3-4.4+10}{\sqrt{9+16}}\) = \(\frac{3}{5}\)

Question 3.
Show that the points (1, 2, 3), (7, 0, 1) and (-2, 3, 4) are collinear.
Solution:
A (1, 2, 3), B(7, 0, 1) C(-2, 3, 4) are the given points.

Question 4.
Find the direction cosines of the normal to the plane x + 2y + 2z – 4 = 0.
Solution:
Equation of the plane is x + 2y + z – 4 = 0
d.r.’s of the normal are (1, 2, 2)
Dividing with \(\sqrt{1+4+4}\) = 3,
d.c.’s of the normal to the plane are \(\left(\frac{1}{3}, \frac{2}{3}, \frac{2}{3}\right)\)

Question 5.
Compute :

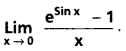
Solution:

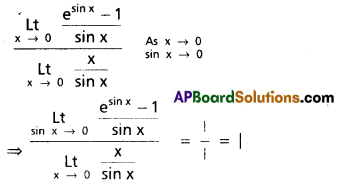
Question 6.
Compute :

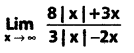
Solution:

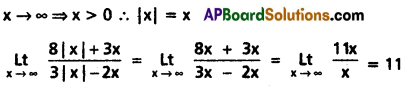
Question 7.
If f(x) = x Tan^-1x, then find f'(x).
Solution:

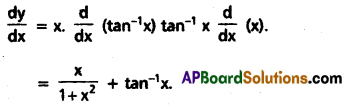
Question 8.
If y = ae^nx + be^-nx, then prove that yⁿ = n²y.
Solution:
y = ae^nx + be^-nx
y₁ = na e^nx – nb e^-nx
y₂ = n².ae^nx + n² be^-nx
y” = n² (ae^nx + b.e^-nx)
= n²y

Question 9.
Find ∆y and dy for the function y = 5x² + 6x + 6 at x = 2 when ∆x = 0.001.
Solution:
∆y = f(x + ∆x) – f(x)
= f(2 + 0.001) – f(2)
= f(2.001) – f(2)
= (5(2.001)² + 6(2.001) + 6) – (5(2)² + 6(2) + 6)
= 20.0200 + 12.0060 + 6 – 20 – 12 – 6
= 0.026005
dy = f(x) ∆x = (10x + 6) ∆x
= (26) (0.001) = 0.0260.

Question 10.
Define strictly increasing function and strictly decreasing function on an interval I.
Solution:
Increasing and decreasing functions :
A function f(x) is
i) Increasing if f'(x) > 0
ii) Decreasing if f'(x) < 0
f(x) is stationary if f'(x) = 0

A function f(x) has local maxima or local minima only at stationary points.
f(x) has local maximum of

1) f'(x) = 0, f”(x) < 0 f(x) has local minimum if
i) f'(x) = 0, f”(x) > 0.
Absolute maximum = max {local maxima}
Absolute minimum = Min {local minima}

Section – B
(5 × 4 = 20)

II. Short Answer type Questions.

1. Attempt any five questions.
2. Each question carries four marks.

Question 11.
A(2, 3) and B(-3, 4) are two given points. Find the equation of locus of P, so that the area of the triangle PAB is 8.5.
Solution:
Let P(x,y) be a point on the locus.
The geometric condition to be satisfied by P is that,
area of ∆PAB = 8.5 ……….. (1)
i.e., \(\frac{1}{2}\) |x(3 – 4) + 2(4 – y) – 3(y – 3) = 8.5
i.e., |-x + 8 – 2y – 3y + 9| = 17
i.e., | -x – 5y + 17| = 17
i.e., -x – 5y + 17 = 17 or -x -5y + 17 = – 17
i.e. x + 5y = 0 or x + 5y = 34
i.e., (x + 5y) (x + 5y – 34) = 0
∴ (x + 5y) (x + 5y – 34) = 0
i.e., x² + 10xy + 25y² – 34x – 170y = 0 …… (2)
Let Q(x₁, y₁) satisfy (2). Then
x₁ + 5y₁ = 0 or x₁ + 5y₁ = 34 ………. (3)
Now, area of ∆QAB

This means that Q(x₁, y₁) satisfies (1).
Hence, the required equation of locus is
(x + 5y) (x + 5y – 34) = 0 or
x² + 10xy + 25y² – 34x – 170y = 0.

Question 12.
When the axes are rotated through an angle 45°, the transformed equation of a curve is 17x² – 16xy + 17y² = 225. Find the original equation of the curve.
Solution:
Angle of rotation = θ = 45
x’ = x cos θ + y sin θ = x cos 45 + y sin 45
= \(\frac{x+y}{\sqrt{2}}\)
y’ = – x sin θ + y cos θ = – x sin 45 + y cos 45
= \(\frac{-x+y}{\sqrt{2}}\)
The original equation of

Question 13.
Find the image of the point (1, 2) in the straight line 3x + 4y – 1 = 0.
Solution:
Equation of the line is 3x + 4y – 1 =0
If (x₂, y₂) is the image of (x₁, y₁) in the line ax + by + c = 0, then

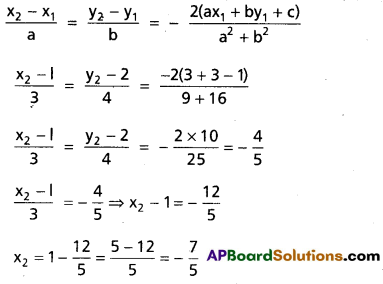
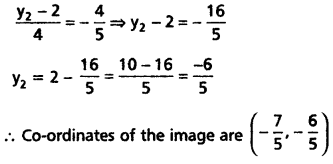
Question 14.
Show that

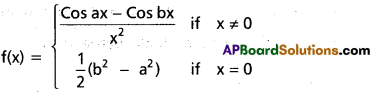
where a and b are real constants, is continuous at ‘0’.
Solution:

Question 15.
Find the derivative of Sin 2x from the First Principle.
Solution:
f(x + h) – f(x) = sin 2 (x + h) – sin 2x
= 2 cos \(\frac{2 x+2 h+2 x}{2}\). sin\(\frac{2 x+2 h-2 x}{2}\)
= 2 cos \(\frac{2x+2 h+2 x}{2}\).sin \(\frac{2 x+2 h-2 x}{2}\)

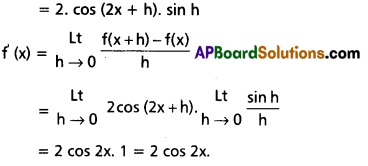
Question 16.
Find the lengths of subtangent, subnormal at a point’t’ on the curve x = a (Cost + t Sint), y = a (Sint – tCost).
Solution:

Question 17.
The volume of a cube is increasing at a rate of 9 cm³/sec. How fast is the surface area increasing when the length of the edge is 10 cm?
Solution:
Let x be the length of the edge of the cube, V be its volume and S be its surface area. Then, V = x³ and S = 6x². Given that rate of change of volume is 9 cm³/sec.
Therefore, \(\frac{d V}{d t}\) = 9 cm³ /sec.
Now, differentiating V w.r.t. t, we get,

Section – C

III. Long Answer Type Questions.

1. Attempt any five questions.
2. Each question carries seven marks.

Question 18.
If p and q are the lengths of the perpendiculars from the origin to the straight lines x Sec α + y Cosec α = a and x Cos α – y Sin α = a Cos 2α, prove that 4p² + q² = a².
Solution:
Equation of AB is x sec α + y cosec α + a
\(\frac{x}{\cos \alpha}+\frac{y}{\sin \alpha}\) = a
x sin α + y cos α – a sin α cos α = 0
P = length of the perpendicular from 0 on AB
= \(\frac{|0+0-a \sin \alpha \cos \alpha|}{\sqrt{\sin ^2 \alpha+\cos ^2 \alpha}}\)
= a sin α. cos α = a. \(\frac{\sin 2 \alpha}{2}\)
2p = a sin 2α …… (1)
Equation of CD is x cos α – y sin α = a cos 2α
x cos α – y sin α – a cos 2α = 0.
q = Length of the perpendicular from 0 on CD
\(\frac{|0+0-a \cos 2 \alpha|}{\sqrt{\cos ^2 \alpha+\sin ^2 \alpha}}\) = a cos 2α ……. (2)
Squaring and adding (1) and (2)
4p² + q² = a² sin² 2α + a² cos² 2α
= a² (sin² 2α + cos² 2α)
= a².1
= a²

Question 19.
If the equation S ≡ ax² + 2hxy + by² + 2gx + 2fy + c = 0 respresents a pair of parallel straight lines, then show that
i) h² = ab,
ii) af² = bg² and
iii) the distance between the parallel lines
= \(2 \sqrt{\frac{g^2-a c}{a(a+b)}}\) = \(\sqrt{\frac{f^2-b c}{b(a+b)}}\)
Solution:
Let the two parallel straight lines represented by s = 0 be
lx + my + n₁ = 0 ………. (1)
and lx + my + n₂ = 0 …….. (2)

(iii) Distance between the parallel lines

Question 20.
Show that the lines joining the origin to the points of intersection of the curve x² – xy + y² + 3x + 3y – 2 = 0 and the straight line x – y – \(\sqrt{2}\) = 0 are mutually perpendicular.
Solution:

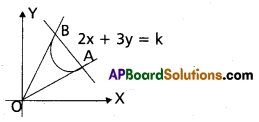
Equation of the curve is
x² – xy + y² + 3x + 3y – 2 = 0 ……….. (1)
Equation of AB is x – y – \(\sqrt{2}\) = 0
x – y = \(\sqrt{2}\)
\(\frac{x-y}{\sqrt{2}}\) = 1 ……… (2)
Homogenising, (1) with the help of (2) combined equation of OA, OB is

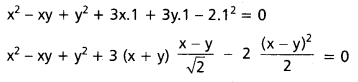
Question 21.
Find the angle between the lines whose direction cosines are given by the equations 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0.
Solution:
Given 3l + m + 5n = 0 ………. (1)
6mn – 2nl + 5lm = 0 ……. (2)
From (1), m = – (3l + 5n)
Substituting in (2)
-6n (3l + 5n) – 2nl – 5l (3l + 5n) = 0
-18ln – 30n² – 2nl – 15l² – 25l = 0
-15l² – 45ln – 30n² = 0
l² + 3ln + 2n² = 0
(l + 2n) (l + n) = 0
l +2n = 0 or l + n = 0

Question 22.
If y =

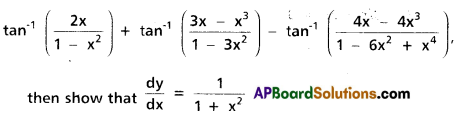
Solution:

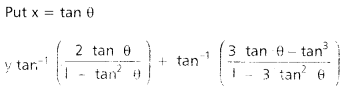
Question 23.
Find the angle between the curves 2y² – 9x = 0, 3x² + 4y = 0 (in the 4^th quadrant).
Solution:
2y² – 9x = 0 ⇒ 9x = 2y²
x = \(\frac{2}{9}\)y²
3×2 + 4y = 0
⇒ 3. \(\frac{4}{81}\)y⁴ + 4y = 0
\(\frac{4 y^4+108}{27}\) = 0
4y(y³ + 27) = 0
y = 0 or y³ = -27 ⇒ y = -3
9x = 2y² = 2 × 9 ⇒ x = 2
Point of intersection (in 4^th quadrant) is P (2, -3)
Equation of the first curve is 2y² = 9x
4y\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 9 ⇒ \(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{9}{4 y}\)
f'(x₁) = \(\frac{9}{4 y}\)

Question 24.
From a rectangular sheet of dimensions 30 cm x 80 cm four equal squares of side x cm are removed at the corners, and the sides are then turned up so as to form an open rectangular box. Find the value of x, so that the volume of the box is greatest.
Solution:
Length of the box =80 – 2x = l

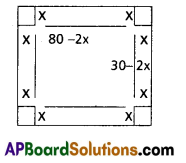
Breadth of the box = 30 – 2x = b
Height of the box = x = h
Volume = lbh = (80 – 2x) (30 – 2x).x
= x (2400 – 220 x + 4x²)
f(x) = 4x³ – 220x² + 2400x