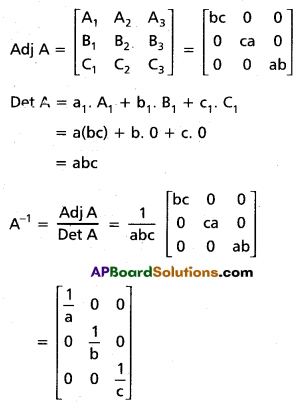
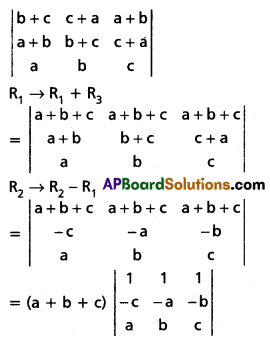
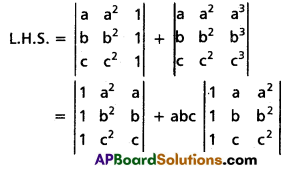
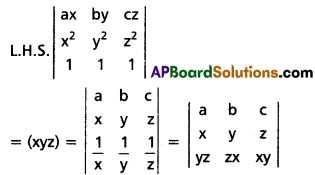
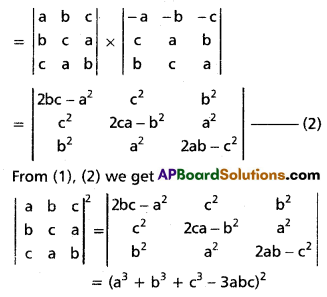
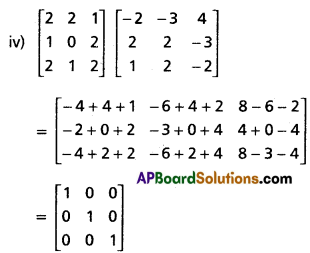
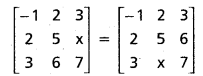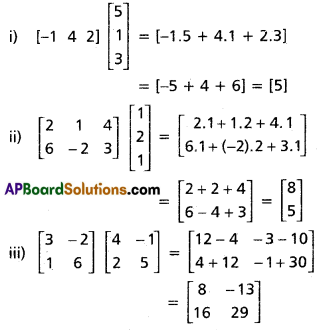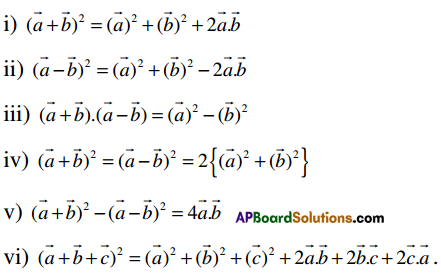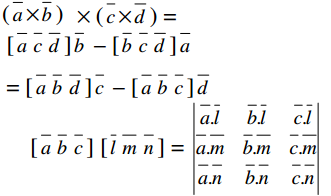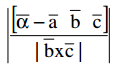Use these Inter 1st Year Maths 1A Formulas PDF Chapter 5 Products of Vectors to solve questions creatively.
Intermediate 1st Year Maths 1A Products of Vectors Formulas
Scalar or Dot Product of Two Vectors:
The scalar or dot product of two non – zero vectors \(\bar{a}\) and \(\bar{b}\), denoted by \(\bar{a} \cdot \bar{b}\) is defined as \(\bar{a} \cdot \bar{b}=|\bar{a}||\bar{b}|\) cos \((\bar{a}, \bar{b})\). This is a scalar, either \(\bar{a}\) = 0 (or) \(\bar{b}\) = 0, then we define \(\bar{a} \cdot \bar{b}\) = 0. If we write \((\bar{a}, \bar{b})\) = 0, then \(\bar{a} \cdot \bar{b}=|\bar{a}||\bar{b}|\) cos θ, if a ≠ 0, b ≠ 0, since 0 ≤ (a, b) = θ ≤ 7 80°, we get
- 0 ≤ θ < 90° ⇒ \(\bar{a}\). b > 0.
- θ = 90° ⇒ \(\bar{a} \cdot \bar{b}\) = 0 and the vectors \(\bar{a}\) and \(\bar{b}\) are perpendicular.
- 90° < θ ≤ 180° ⇒ \(\bar{a} \cdot \bar{b}\) < 0
- \(\bar{a} \cdot \bar{b}=\bar{b} \cdot \bar{a}\)
- a̅ (b̅ + c̅) = a̅ .b̅ + a̅ .c̅
- If a̅, b̅ are parallel, a̅.b̅ = ± |a̅ | |b̅ |.
- If l, m ∈ R, (la̅).(mb̅) = lm(a̅. b̅)
- Projection of b̅ on a̅ (or) length of the projection a̅ = \(\frac{|\bar{a} \cdot \bar{b}|}{|\bar{a}|}\)
- Orthogonal projection of b̅ on a̅ = \(\frac{(\bar{a} \cdot \bar{b})_{\bar{a}}}{|\bar{a}|^{2}}\); a̅ ≠ 0
or
The projection vector b̅ on a̅ = \(\left(\frac{\bar{a} \cdot \bar{b}}{|\bar{a}|^{2}}\right)\) a̅ and it is magnitude = \(\frac{|\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}|}{|\overline{\mathrm{a}}|}\)
- The component vector of b̅ along a̅ (or) parallel to a̅ is \(\left(\frac{\bar{a} \cdot \bar{b}}{|\bar{a}|^{2}}\right)\)a̅
Component vector of a̅ along b̅ = \(\frac{(\bar{a} \cdot \bar{b}) \bar{b}}{|\bar{b}|^{2}}\), component vector of a̅ perpendicular to b̅ = a̅ – \(\frac{(\bar{a} \cdot \bar{b}) \bar{b}}{|\bar{b}|^{2}}\)

Orthogonal unit vectors :
Ifi, j, k are orthogonal unit vector triad in a right handed system, then
- i̅ .j̅ = j̅.k̅ = k̅.i̅ = 0
- i̅ .i̅ = j̅.j̅ = k̅.k̅ = 1
- If r is any vector, r̅ = (r̅.i̅)i̅ +(r̅.j̅)j̅ ≠ (r̅.k̅)k̅
Some identities :
If a̅, b̅, c̅ are three vectors, then
- (a̅ + b̅)2 = |a̅|2 + |b̅|2 + 2(a̅ . b̅)
- (a̅ – b̅)2 = |a̅|2 + |b̅|2 – 2(a̅.b̅)
- (a̅ + b̅)2 + (a̅ – b̅)2 = 2(|a̅|2 + |b̅|2)
- (a̅ + b̅)2 – (a̅ – b̅)2 = 4(a̅. b̅)
- (a̅ + b̅). (a̅ – b̅) = |a̅|2 – |b̅|2
- (a̅ + b̅ + c̅)2 = |a̅|2 + |b̅|2 + |c̅|2 + 2(a̅ . b̅) + 2(b̅ . c̅) + 2(c̅ .a̅)
→ If a̅ = a1 i̅ +a2j̅ + a3k̅ and b̅ = b1i̅ + b2j̅ + b3k̅, then
a̅.b̅ = a1b1 + a2b2 + a3b3
a̅ is perpendicular to b̅
⇔ a1b1 + a2b2 + a3b3 = 0
→ |a̅| = \(\), |b̅| = \(\)
→ If (a̅, b̅) = then cos θ = \(\frac{\bar{a} \cdot \bar{b}}{|\bar{a}||\bar{b}|}=\frac{a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}}{\sqrt{\sum a_{1}^{2}} \sqrt{\sum b_{1}^{2}}}\) and sin θ = \(\sqrt{\frac{\sum\left(a_{2} b_{3}-a_{3} b_{2}\right)^{2}}{\left(\sum a_{1}^{2}\right)\left(\sum b_{1}^{2}\right)}}\)
→ a̅ is parallel to b̅ ⇔ a1: b1 = a2 : b2 = a3: b3
→ a̅.a̅ >0; |a̅.b̅| < |a̅| |b̅|
|a̅ + b̅| ≤ |a̅| + |b̅|; |a̅ – b̅| ≤ |a̅| + |b̅| ;
|a̅ – b̅| ≥ |a̅| – |b̅|
Vector equations of a plane :
- The equation of the plane, whose perpendicular distance from the origin is p and whose unit normal drawn from the origin towards the plane is h is n̂ is r̅.n̂ = p.
- Equation of a plane passing through the origin and perpendicular to the unit vector n̅, is r̅.n̅ = 0
- Vector equation of a plane passing through a point A with position vector a and perpendicular to a vector n̅ is (r – a̅). n̅ = 0.
Perpendicular distance from the origin to the plane (r̅ – a̅).h = 0 is a̅. n̅ . where ‘a̅’ is the position vector of A in the plane and ‘n̅’ is a unit vector perpendicular to the plane.
Angle between two planes :
If π1 and π22 be two planes and \(\bar{M}_{1}, \bar{M}_{2}\) are normals drawn to them, we define the angle between M1 and M2 as the angle between π1 and π2. If the angle between \(\) and \(\) is θ, the angle between the given planes θ = cos-1\(\left[\frac{\bar{M}_{1} \cdot \bar{M}_{2}}{\left|\bar{M}_{1}\right|\left|\bar{M}_{2}\right|}\right]\)
Work done by a constant force F:
- If a constant force F̅ acting on a particle displaces it from a position ‘A’ to the position B, then the work done ‘W by this constant force T is the dot product of the vectors
representing the force F̅ and displacement \(\overline{A B}\), i.e., W = F̅.\(\overline{A B}\).
- If F is the resultant of the forces F̅1, F̅2, ……………….F̅n, then workdone in displacing the particle from A to B is
\(\bar{W}=\bar{F}_{1} \cdot \overline{A B}+\bar{F}_{2} \cdot \overline{A B}+\ldots \ldots+F_{n} \cdot \overline{A B}\)
Cross Product or Vector Product of two vectors :
The vector product or cross product of two non-parallel non – zero vectors ‘a̅’ and ‘b̅’ is defined as a̅ × b̅ = |a̅||b̅| sin θ n̂, where ‘ n̂’ is a unit vector perpendicular to the plane containing ‘a̅’ and ‘b̅’ such that a̅, b̅ and ‘n̂’ form a vector triad in the right handed system and (a̅, b̅) = θ, this is a vector. If either of a̅, b̅ is a zero vector or ‘a̅’ is parallel to ‘b̅’, we define a̅ × b̅ = 0.
Some important results on vector product:
- |a̅ × b̅| = |a̅||b̅|sinθ ≤ |a̅||b̅| ;
- |a̅ × b̅| = |b̅ × a̅|
- a̅ × b̅ = -(b̅ × a̅):
- -a̅ × -b̅ = a̅ × b̅
- (-a̅) × b̅ = a̅ × (-b̅) – (a̅ × b̅)
- la̅ × mb̅ = lm(a̅ × b̅) ;
- a̅ × (b̅ + c̅) = a̅ × b̅ + a̅ × c̅
- a̅ ≠ 0, b̅ ≠ 0 and a̅ × b̅ = 0 ⇔ ‘a̅’ and ‘b̅’ are parallel vectors.
- a̅, b̅ , c̅ are non-zero vectors and a̅ × c̅ = b̅ × c̅ ⇒ either a̅ = b̅ or a̅ – b̅ is parallel to c̅.
Vector product among i. i and k:
If i̅, j̅ and k̅ are orthogonal unit vectors triad in the right handed system then
- i̅ × j̅ = j̅ × j = k̅ × k̅ = 0
- i̅ × j̅ = k̅ =-j̅ × i̅ ; j̅ × k̅ = k̅ × j̅ = i̅ ; k̅ × i̅ = -i̅ × k̅ = j̅
- If a̅ = a1 i̅ + a2 j + a3k ; b̅ = b1i̅ + b2 j̅ + b3k̅, then
a̅ × b̅ = a2b3 – a3b2)i̅ + (a3b1 – a1b3)j̅ + (a1b2 – a2b1)k̅
This may be represented in the form of a determinants as a̅ × b̅ = \(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right|\)
- Unit vectors perpendicular to both ‘a̅’and ‘b̅’ are ± \(\frac{\bar{a} \times \bar{b}}{|\bar{a} \times \bar{b}|}\)
- If a̅ = a1i̅ + a2j̅ + a3k̅ ; b̅ = b1i̅ + b2 j̅ + b3k̅ and (a̅, b̅) = θ, then
sin θ = \(\frac{\sqrt{\sum\left(a_{2} b_{3}-a_{3} b_{2}\right)^{2}}}{\sqrt{\sum a_{1}^{2}} \sqrt{\sum b_{1}^{2}}}\) cos θ = \(\frac{a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}}{\sqrt{\sum a_{1}^{2}} \sqrt{\sum b_{1}^{2}}}\)

Vector areas:
- If \(\overline{A B}=\bar{c}\) and \(\overline{A C}=\bar{b}\) are two adjacent sides of a triangle ABC, then vector area of ΔABC = \(\frac{1}{2}\)(c̅ × b̅) and the area of the ΔABC = \(\frac{1}{2}\)|c̅ × b̅| $q. units.
- If a̅, b̅, c̅ are the position vectors of A, B, C respectively then the vector area of
ΔABC = \(\frac{1}{2}\)[(b̅ × c̅) + (c̅ × a̅) + (a̅ × b̅)]
Area of ΔABC = \(\frac{1}{2}\)|(b̅ × c̅) + (c̅ × a̅) + (a̅ × b̅)|sq. units.
- If \(\) and \(\) are the diagonals of a parallelogram ABCD, then the vector area of the parallelogram = \(\frac{1}{2}\)|a̅ × b̅| and area = \(\frac{1}{2}\)|a̅ × b̅|sq. units.
- If AB = a̅ and AD = b̅ are two adjacent sides of a parallelogram ABCD, then its vector area = a̅ × b̅ and area = |a̅ × b̅| sq. units.
- Vector area of the quadrilateral ABCD = \(\frac{1}{2}\)\((A C \times B D)\) and area of the quadrilateral ABCD = \(\frac{1}{2}\)\(|\overline{A C} \times \overline{B D}|\)sq. units.
Some useful formulas :
- If a̅, b̅ are two non-zero and non-parallel vectors then
(a̅ × b̅)2 = a2b2 – (a̅.b̅)2 = \(\left|\begin{array}{cc}
a \cdot \bar{a} & \bar{a} \cdot \bar{b} \\
\bar{a} \cdot b & b \cdot \bar{b}
\end{array}\right|\)
- For any vector a̅,(a̅ × i̅)2 + (a̅ × j̅)2 + (a̅ × k̅)2 = 2|a|2
- If a̅, b̅, c̅ are the position vectors of the points A, B, C respectively, then the perpendicular distance from c to the line AB is \(\frac{|\overline{A C} \times \overline{A B}|}{|\overline{A B}|}=\frac{|(\bar{b} \times \bar{c})+(\bar{c} \times \bar{a})+(\bar{a} \times \bar{b})|}{|b-\bar{a}|}\)
Moment of a force :
Let 0 be the point of reference (origin) and \(\overline{o p}=\bar{r}\) be the position vector of a point p on the line of action of a force F̅. Then the moment of the force F about 0 is given by r̅ × F̅.
Scalar triple product:
Let a̅, b̅, c̅ he three vectors. We call (a̅ × b̅). c̅ the scalar product of a̅, b and c. This is a scalar (real number). It is written as [a̅ b̅ c̅]
- If (a̅ × b̅). c̅ = 0, then one or more of the vectors a̅, b̅ and c̅ should be zero vectors. If a ≠ 0, b ≠ 0, c ≠ 0, then c is perpendicular to a̅ × b̅. Hence the vector c̅ lies on the plane determined by a̅ and b̅. Hence a̅, b̅ and c̅ are coplanar.
- If in a scalar triple product, any two vectors are parallel (equal), then the scalar triple product is zero i.e., [a̅ a̅ b̅] = [a̅ b̅ b̅] = [c̅ b̅ c̅] = 0.
- In a scalar triple product remains unaltered if the vectors are permutted cyclically i.e., [a̅ b̅ c̅] = [b̅ c̅ a̅] = [c̅ a̅ b̅].
However [a̅ b̅ c̅] = -[b̅ a̅ c̅] = -[c̅ b̅ a̅] = -[a̅ c̅ b̅].
- In a scalar triple product, the dot and cross are interchangeable i.e., a̅.b̅ × c̅ = a̅ × b̅.c̅
→ If i̅ , j̅ , k̅ are orthogonal unit vector triad in the right handed system, then
- [i̅ j̅ k̅ ] = [j̅ k̅ i̅ ] = [k̅ i̅ j̅ ] = 1
- [i̅ k̅ j̅ ] = [j̅ i̅ k̅ ] = [k̅ j̅ i̅ ] = -1
- If a̅ = a1 i̅ + a2j̅ + a3 k̅ ; b̅ = b1i̅ + b2 j̅ + b3k̅ and c̅ = c1i̅ + c2 j̅ + c3k̅ then [a̅ b̅ c̅] = \(\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\)

→ A necessary and sufficient condition that three non-parallel (non-collinear) and non-zero vectors a, b and c to be coplanar is [a̅ b̅ c̅] = 0. If [a̅ b̅ c̅] ≠ 0, then the three vectors are non-coplanar.
→ If a̅, b̅, c̅ are three non-zero, non-coplanar vectors and V is the volume of the parallelopiped with co-terminus edges a̅, b̅ and c̅, then v = |(a × b). c|. = |[a b c]|
→ The volume of the parallelopiped formed with A, B, C, D as vertices is \(|[A B A C A D]|\) cubic units.
→ If a̅, b̅, c̅ represent the co-terminus edges of a tetrahedron, then its volume = \(\frac{1}{6}\)[a̅, b̅, c̅] cubic units.
→ If A(x1 y1 z1], B(x2, y2, z2] C(x3 y3 z3) and D(x4, y4 z4] are the vertices of a tetrahedron = \(\frac{1}{6}\)\(|[A B A C A D]|\)
- Vector equation of a plane containing three non-collinear points a̅, b̅, c̅ is r̅ .[(b̅ × c̅) + (c̅ × a̅) + (a̅ × b̅)] = [a̅ b̅ c̅]
- A unit vector perpendicular to the plane containing three non-collinear points a̅, b̅, c̅ is \(\frac{(\bar{a} \times b)+(b \times \bar{c})+(\bar{c} \times \bar{a})}{|(\bar{a} \times \bar{b})+(b \times \bar{c})+(\bar{c} \times a)|}\)
- Length of the perpendicular from the origin to the plane containing three non-collinear points a̅, b̅, c̅ is \(\frac{|[\bar{a} b c]|}{|(\bar{a} \times \bar{b})+(\bar{b} \times \bar{c})+(\bar{c} \times \bar{a})|}\)
→ Vector equation of the plane passing through three non-collinear points a̅, b̅ and c̅ is [r̅ – a̅ b̅ – a̅ c̅ – a̅] = 0
→ Vector equation of the plane passing through a given point a̅ and parallel to the vectors b̅ and c̅ is [r b̅ c̅] = [a̅ b̅ c̅]
→ Vector equation of the line passing through the point a̅ and parallel to the vector b̅ is (r – a̅) × b̅ = 0
→ Distance of the point p(c) from a line joining the points A(a) and B(b) = |(c̅ – a̅) × b̅|
(25) i) Equation of the plane passing through the point p(x1, y1, z1) and perpendicular to the vector ai̅ + bj̅ + ck̅ is a (x – x1) + b(y – y1) + c(z – z1) = 0.
→ The equation of the plane passing through the points (x1 y1 z1), (x2, y2, z2) and
(x3, y3, z3) is \(\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1}
\end{array}\right|\) = 0
Skew lines:
Two lines l and m are called skew lines if there is no plane passing through these lines.
Shortest distance between the skew lines:
Shortest distance between the skew lines r̅ = a̅ + tb̅ and r̅ = c̅ + sd̅ is

Vector triple product:
If a̅, b̅ and c̅ are three vectors, products of the type (a̅ × b̅) × c̅, a̅ × (b̅ × c̅) from the vector triple products. From this definition.
- If any one of a̅, b̅ and c̅ is a zero vector, a̅ × (b̅ × c̅) or (a̅ × b̅) c̅ = 0
- If a̅ ≠ 0, b̅ ≠ 0, c̅ ≠ 0 and a̅ is parallel to b, then (a̅ × b̅) × c̅ = 0
- If a̅ ≠ 0, b̅ ≠ 0, c̅ ≠ 0 and c̅ is perpendicular to the plane of a and b, then (a̅ × b̅) × c̅ = 0.
→ If a̅ ≠ 0, b̅ ≠ 0, c̅ ≠ 0, a̅ and b̅ are non-parallel vectors and c̅ is not perpendicular to the plane passing through a̅ and b, then
(a̅ × b̅) × c̅ = (a̅.c̅)b̅ – (b̅.c)a̅
a̅ × (b̅ × c̅) = (a̅.c̅)b̅ – (a.b̅)c̅
- In general, vector triple product of three vectors need not satisfy the associative law. i.e., (a̅ × b) × c ≠ a̅ × (b × c)
For any three vectors a̅, b̅ and c
- a̅ × (b̅ × c̅) + b̅ × (c̅ × a̅) + c̅ × (a̅ × b̅) = 0
- [a̅ × b̅ b̅ × c̅ c̅ × a̅] = [a̅ b̅ c̅]2
Scalar product of four vectors :
Scalar product of a̅, b̅, c̅ and d̅ is () = (a̅. c̅) (b̅.d̅) – (a̅. d̅) (b̅ .c̅) = \(\left|\begin{array}{ll}
\bar{a} \cdot \bar{c} & \bar{a} \cdot \bar{d} \\
\bar{b} \cdot \bar{c} & \bar{b} \cdot \bar{d}
\end{array}\right|\)
Vector product of four vectors:
If a̅, b̅, c̅ and d̅ are four vectors,
(a̅ × b̅) × (c̅ × d̅) = [a̅ c̅ d̅] b̅ – [b̅ c̅ d̅]a̅ – [a b̅ d̅]c̅ – [a̅ b̅ c̅]d̅
Some important results:
- [a̅ + b̅ b̅ + c̅ c̅ + a̅] = 2[a̅ b̅ c̅]
- i̅ × (j̅ × k̅) + i̅ × (k̅ × i̅) + k̅ × (i̅ × j̅) = 0
- [a̅ × b̅ b̅ × c̅ c̅ × a̅] = [a̅ b̅ c̅]2
[a̅ b̅ c̅] [l̅ m̅ n̅] = \(\)
- If a̅, b̅, c̅ be such that a is perpendicular to (b̅ + c̅), bis perpendicular to (c̅ + a̅), c̅ is perpendicular to (a̅ + b̅), then |a̅ + b̅ + c̅| = \(\sqrt{a^{2}+b^{2}+c^{2}}\)
- If a line makes angles α, β, γ and δ with the diagonals of a cube, then
cos2α + cos2β + cos2γ + cos2δ = \(\frac{4}{3}\)
- i̅ × (a̅ × i̅) + j̅ × (a̅ × j̅) + k̅ × (a̅ × k̅) – 2a̅
→ Equation of the sphere with centre at c and radius ‘a’ is r2 – 2r̅. c̅ + c2 = a2

Scalar Product
Def: Let \(\vec{a}, \vec{b}\) be two vectors dot product (or) scalar product (or) direct product (or) inner product denoted by \(\vec{a}, \vec{b}\). Which is defined as \(|\vec{a}||\vec{b}|\)cos θ where cos θ = \((\vec{a}, \vec{b})\)
* The product \(\vec{a}, \vec{b}\) is zero when \(|\vec{a}|\) = 0 (or) \(|\vec{b}|\) = 0 (or) θ = 90°.
Sign of the scalar product :
Let \(\vec{a}, \vec{b}\) are two non-zero vectors
- If θ is acute then \(\vec{a}.\vec{b}\)> 0 (i.e 0 < θ < 90°).
- If θ is obtuse then \(\vec{a}.\vec{b}\) < 0 (i.e 90° < θ < 180°).
- If θ = 90° then\(\vec{a} \cdot \vec{b}\) = o.
- If θ = 0° then \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\)
- If θ = 180° then \(\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|\)
Note:
- The dot product of two vectors is always scalar.
- \(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\) i.e dot product of two vectors is commutative.
- If \(\vec{a} \cdot \vec{b}\) are two vectors then \(\vec{a} \cdot(-\vec{b})=(-\vec{a}) \cdot \vec{b}=-(\vec{a} \cdot \vec{b})\)
- \((-\vec{a}) \cdot(-\bar{b})=\vec{a} \cdot \vec{b}\)
- If l,m are two scalars and \(\vec{a} \cdot \vec{b}\) are two vectors then \((l \bar{a}) \cdot(m \bar{b})={lm}(\vec{a} \cdot \vec{b})\)
- If \(\vec{a}\) and \(\vec{b}\) are two vectors then \(\vec{a} \cdot \vec{b}=\pm|\vec{a}||\vec{b}|\)
- If \(\vec{a}\) is a vector then \(\vec{a} \cdot \vec{a}=|\vec{a}|^{2}\)
- If \(\vec{a}\) is a vector \(\vec{a}\).\(\vec{a}\) is denoted by \(\overline{(a)^{2}}\) hence \(\overline{(a)^{2}}=|\vec{a}|^{2}\)
Components and orthogonal projection:
Def: Let \(\vec{a}=\overline{O A} \quad \vec{b}=\overline{O B}\) be two non zero vectors let the plane passing through B and perpendicular to a intersect \(\overline{O A}\) ln M.
- If \((\vec{a}, \vec{b})\) is acute then OM is called component of \(\vec{b}\) on \(\vec{a}\).
- If \((\vec{a}, \vec{b})\) is obtuse then -(OM) is called the component of \(\vec{b}\) on \(\vec{a}\).
- The vector \(\overline{O M}\) is called component vector of \(\vec{b}\) on \(\vec{a}\).

Def: Let \(\vec{a}=\overline{O A}\); \(\vec{b}=\overrightarrow{P Q}\) be two vectors let the planes passing through P, Q and perpendicular to a intersect \([latex]\)[/latex] in L, M respectively then \(\overline{L M}\) is called orthogonal projection of \(\vec{b}\) on \(\vec{a}\)
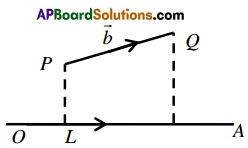
Note:
- The orthogonal projection of a vector b on a is equal tb component vector of b on a .
- Component of a vector \(\vec{b}\) on \(\vec{a}\) is also called projection of \(\vec{b}\) on \(\vec{a}\)
- If A< B, C, D are four points in the space then the component of \(\overline{A B}\) on \(\overline{C D}\) is same as the projection of \(\overline{A B}\) on the ray \(\overline{C D}\).
→ If \(\vec{a}, \vec{b}\) be two vectors (\(\vec{a} \neq \vec{o}\)) then
- The component of \(\vec{b}\) on \(\vec{a}\) is \(\frac{\vec{b} \cdot \vec{a}}{|\vec{a}|}\)
- The orthogonal projection of \(\vec{b}\) on \(\vec{a}\) is \(\frac{(\vec{b} \cdot \vec{a}) \vec{a}}{|\vec{a}|^{2}}\)
→ If \(\vec{i}, \vec{j}, \vec{k}\) form a right handed system of Ortho normal triad then
- \(\vec{i} \cdot \vec{j}=\vec{j} \cdot \vec{j}=\vec{k} \cdot \vec{k}\) = 1
- \(\vec{i} \cdot \vec{j}=\vec{j} \cdot \vec{i}=0 ; \vec{j} \cdot \vec{k}=\vec{k} \cdot \vec{j}=0 ; \vec{k} \cdot \vec{i}=\vec{i} \cdot \vec{k}=0\)
→ If \(\vec{a}=a_{1} \vec{i}+a_{2} \vec{j}+a_{3} \vec{k}\) \(\vec{b}=b_{1} \vec{i}+b_{2} \vec{j}+b_{3} \vec{k}\) then \(\vec{a} \cdot \vec{b}=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}\)
→ If \(\vec{a}, \vec{b}, \vec{c}\) are three vectors then
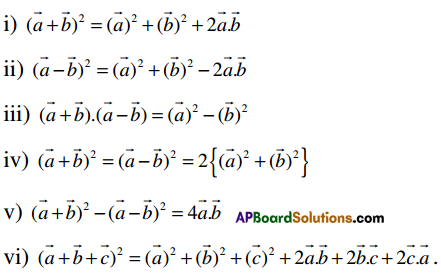
→ If \(\vec{r}\) is vector then \(\vec{r}=(\vec{r} \cdot \vec{i}) i+(\vec{r}+\vec{j}) \vec{j}+(\vec{r} \cdot \vec{k}) \vec{k}\)
Angle between the planes:
The angle between the planes is defined as the angle between the normals to the planes drawn from any point in the space.
Sphere:
The vector equation of a sphere with centre C having position vector \(\vec{c}\) and radius a is \((\vec{r}-\vec{c})^{2}\) = a2 i.e. \(\vec{r}^{2}-2 \vec{r} \cdot \vec{c}+c^{2}\) = a2
The vector equation of a sphere with A(a) and B(b) as the end points of a diameter is \((\vec{r}-\vec{a}) \cdot(\vec{r}-\vec{b})\) = 0 (or) \((\vec{r})^{2}-\vec{r} \cdot(\vec{a}+\vec{b})+\vec{a} \cdot \vec{b}\) = 0

Work done by a force :
If a force \(\vec{F}\) acting on a particle displaces it from a position A to the position B then work done W by this force \(\vec{F}\) is \(\vec{F} \cdot \overline{A B}\)
- The vector equation of the plane which is at a distance of p from the origin along the unit vector \(\vec{n}\) is \(\vec{r} \cdot \vec{n}\) = p.
- The vector equation of the plane passing through the origin and perpendicular to the vector m is r.m =0
- The Cartesian equation of the plane which is at a distance of p from the origin along the unit vector n = li + mj + nk of the plane is n = lx + my + nz
- The vector equation of the plane passing through the point a having position vector \(\vec{a}\) and perpendicular to the vector \(\vec{m}\) is \((\vec{r}-\vec{a}) \cdot \vec{m}\) = 0.
- The vector equation of the plane passing through the point a having position vector \(\vec{a}\) and parallel to the plane r.m=q is \((\vec{r}-\vec{a}) \cdot \vec{m}\) = 0.
Cross( Vector) Product of Vectors:
Let \(\vec{a}, \vec{b}\) be two vectors. The cross product or vector product or skew product of vectors \(\vec{a}, \vec{b}\) is denoted by \(\vec{a} \times \vec{b}\) and is defined as follows
- If \(\vec{a}\) = 0 or \(\vec{b}\) = 0 or \(\vec{a}, \vec{b}\) are parallel then \(\vec{a} \times \vec{b}\) = 0
- If \(\vec{a}\) ≠ 0, \(\vec{b}\) ≠ 0, \(\vec{a}, \vec{b}\) are not parallel then \(\vec{a} \times \vec{b}=|\vec{a}||\vec{b}|(\sin \theta) \vec{n}\) where \(\vec{n}\) is a unit vector perpendicular to a and b so that a, b, n form a right handed system.
Note:
- \(\vec{a} \times \vec{b}\) is a vector
- If \(\vec{a}, \vec{b}\) are not parallel then \(\vec{a} \times \vec{b}\) is perpendicular to both a and b
- If \(\vec{a}, \vec{b}\) are not parallel then \(\vec{a}, \vec{b}\) , \(\vec{a} \times \vec{b}\) form a right handed system .
- For any vector \(\vec{a}\) \(\vec{a} \times \vec{b}\) = o
2. If \(\vec{a}, \vec{b}\) are two vectors \(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\) this is called “anti commutative law”
3. If \(\vec{a}, \vec{b}\) are two vectors then \(\vec{a} \times(-\vec{b})=(-\vec{a}) \times \vec{b}=-(\vec{a} \times \vec{b})\)
4. If \(\vec{a}, \vec{b}\) are two vectors then \((-\vec{a}) \times(-\vec{b})=\vec{a} \times \vec{b}\)
5. If \(\vec{a}, \vec{b}\) are two vectors l,m are two scalars then (la) x (mb) = lm(a x b)
6. If \(\vec{a}, \vec{b}, \vec{b}\) are three vectos, then
- \(\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}\)
- \((\vec{b}+\vec{c}) \times \vec{a}=\vec{b} \times \vec{a}+\vec{c} \times \vec{a}\)
7. If \(\vec{l}, \vec{l}, \vec{k}\) from a right handed system of orthonormal triad then
- \(\vec{l} \times \vec{l}=\vec{j} \times \vec{j}=\vec{k} \times \vec{k}=\vec{o}\)
- \(\vec{i} \times \vec{j}=\vec{k}=-\vec{j} \times \vec{l} ; \vec{j} \times \vec{k}=\vec{l}=-\vec{k} \times \vec{j} ; \vec{k} \times \vec{l}=\vec{j}=-\vec{l} \times \vec{k}\)
→ If \(\vec{a}=a_{1} \vec{l}+a_{2} \vec{j}+a_{3} \vec{k}, \vec{b}=b_{1} \vec{l}+b_{2} \vec{j}+b_{3} \vec{k}\) then \(\vec{a} \times \vec{b}=\left|\begin{array}{ccc}
\vec{l} & \vec{j} & \vec{k} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right|\)

→ If \(\vec{a}=a_{1} \vec{l}+a_{2} \vec{m}+a_{3} \vec{n}, \quad \vec{b}=b_{1} \vec{l}+b_{2} \vec{m}+b_{3} \vec{n}\) where \(\vec{l}, \vec{m}, \vec{n}\) form a right system of non coplanar vectors then \(\)
→ If \(\vec{a}, \vec{b}\) are two vectors then \((\vec{a} \times \vec{b})^{2}+(\vec{a} \cdot \vec{b})^{2}\) = a2b2.
Vector Area:
If A is the area of the region bounded by a plane curve and \(\vec{n}\) is the unit vector perpendicular to the plane of the curve such that the direction of curve drawn can be considered anti clock wise then A\(\vec{n}\) is called vector area of the plane region bounded by the curve.
- The vector area of triangle ABC is \(\frac{1}{2} \overline{A B} \times \overrightarrow{A C}=\frac{1}{2} \overrightarrow{B C} \times \overrightarrow{B A}=\frac{1}{2} \overline{C A} \times \overrightarrow{C B}\)
- If \(\vec{a}, \vec{b}, \vec{c}\)are the position vectors of the vertices of a triangle then the vector area of the triangle is \(\frac{1}{2}(\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a})\)
- If ABCD is a parallelogram and \(\overrightarrow{A B}=\vec{a}, \quad \overrightarrow{B C}=\vec{b}\) then the vector area of ABCD is \(\vec{a} \times \vec{b}\).
- If ABCD is a parallelogram and \(\overrightarrow{A C}=\vec{a}, \overrightarrow{B C}=\vec{b}\) then vector area of parallelogram ABCD is \(\frac{1}{2}(\vec{a} \times \vec{b})\)
- The vector equation of a line passing through the point A with position vector a and perpendicular to the vectors \(\vec{b} \times \vec{c}\) is \(\vec{r}=\vec{a}+t(\vec{b} \times \vec{c})\).
Scalar Triple Product:
- If \(\vec{a}, \vec{b}, \vec{c}\) are the three vectors, then the real numbers \((\vec{a} \times \vec{b}) \cdot \vec{c}\) is called scalar triple product denoted by \([\vec{a} \vec{b} \vec{c}]\). This is read as ‘box’ \(\vec{a}, \vec{b}, \vec{c}\)
- If V is the volume of the parallelepiped with coterminous edges a, b, c then V = |\([\vec{a} \vec{b} \vec{c}]\)|
- If \(\vec{a}, \vec{b}, \vec{c}\) form the right handed system of vectors then V = \([\vec{a} \vec{b} \vec{c}]\)
- If \(\vec{a}, \vec{b}, \vec{c}\) form left handed system of vectors then -V = \([\vec{a} \vec{b} \vec{c}]\)
Note:
- The scalar triple product is independent of the position of dot and cross. i.e. \(\vec{a} \times \vec{b} \cdot \vec{c}=\vec{a} \cdot \vec{b} \times \vec{c}\)
- The value of the scalar triple product is unaltered so long as the cyclic order remains unchanged
\([\vec{a} \vec{b} \vec{c}]=[\vec{b} \vec{c} \vec{a}]=[\vec{c} \vec{a} \vec{b}]\)
- The value of a scalar triple product is zero if two of its vectors are equal
\([\vec{a} \vec{a} \vec{b}]\)= 0 \([\vec{b} \vec{b} \vec{c}]\) = 0
- If a, b, c are coplanar then \([\vec{a} \vec{b} \vec{c}]\) = 0
- If a,b,c form right handed system then \([\vec{a} \vec{b} \vec{c}]\) > 0
- If a,b,c form left handed system then \([\vec{a} \vec{b} \vec{c}]\) < 0
- The value of the triple product changes its sign when two vectors are interchanged
\([\vec{a} \vec{b} \vec{c}]\) = –\([\vec{a} \vec{c} \vec{b}]\)
- If l,m, n are three scalars \(\vec{a}, \vec{b}, \vec{c}\) are three vectors then \(\)
→ Three non zero non parallel vectors abc nare coplanar iff \([l \vec{a} m \vec{b} \quad n \vec{c}]={lmn}\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right]\)= 0
→ If \(\vec{a}=a_{1} \vec{l}+a_{2} \vec{m}+a_{3} \vec{n}, \vec{b}=b_{1} \vec{l}+b_{2} \vec{m}+b_{3} \vec{n}, \vec{c}=c_{1} \vec{l}+c_{2} \vec{m}+c_{3} \vec{n}\) where \(\vec{l}, \vec{m}, \vec{n}\) form a right handed system of non coplanar vectors, then \([\vec{a} \vec{b} \vec{c}]=\left|\begin{array}{ccc}
\vec{m} \times \vec{n} & \vec{n} \times \vec{l} & \vec{l} \times \vec{m} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|\)
→ The vectors equation of plane passing through the points A, B with position vectors \(\vec{a}, \vec{b}\) and parallel to the vector \(\vec{c}\) is \([\vec{r}-\vec{a} \vec{b}-\vec{a} \vec{c}]\) (or) \([\vec{r} \vec{b} \vec{c}]+[\vec{r} \vec{c} \vec{a}]=\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right]\)
→ The vector equation of the plane passing through the point A with position vector \(\vec{a}\) and parallel to \(\vec{b}, \vec{c}\) is \([\vec{r}-\vec{a} \vec{b} \vec{c}]\) = 0 i.e. \(\left[\begin{array}{lll}
\vec{r} & \vec{b} & \vec{c}
\end{array}\right]=\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right]\)

Skew lines:
Two lines are said to be skew lines if there exist no plane passing through them i.e. the lines lie on two difference planes
Def:- l1 and l2 are two skew lines. If P is a point on l1 and Q is a point on l2 such that \(\overleftarrow{P Q}\) ⊥ l1 and PQ ⊥ l2 then \(\overleftarrow{P Q}\) is called shortest distance and \(\overleftarrow{P Q}\) is called shortest distance line between the lines l1 and l2.
The shortest distance between the skew lines \(\vec{r}=\vec{a}+t \vec{b}\) and \(\vec{r}=\vec{c}+t \vec{d}\) is \(\frac{|[\vec{a}-\vec{c} \vec{b} \vec{d}]|}{|\vec{b} \times \vec{d}|}\)
Vector Triple Product:
Cross Product of Three vectors : For any three vectors \(\bar{a}, \bar{b}\) or \(\bar{c}\) then cross product or vector product of these vectors are given as \(\bar{a} \times(\bar{b} \times \bar{c}),(\bar{a} \times \bar{b}) \times \bar{c}\) or \((\bar{b} \times \bar{c}) \times \bar{a}\) etc.

vi. If \(\bar{a}, \bar{b}\) or \(\bar{c}\) are non zero vectors and \(\) then b and c are parallel (or collinear) vectors.
vii. If \(\bar{a}, \bar{b}\) or \(\bar{c}\) are non zero and non parallel vectors then \(\bar{a} \times(\bar{b} \times \bar{c}), \quad \bar{b} \times(\bar{c} \times\bar{a})\) and \(\bar{c} \times(\bar{a} \times \bar{b})\) are non collinear vectors.
viii. If \(\bar{a}, \bar{b}\) or \(\bar{c}\) are any three vectors then \(\bar{a}(\bar{b} \times \bar{c})+\bar{b} \times(\bar{c} \times \bar{a})+\bar{c} \times(\bar{a} \times \bar{b})=\overline{\mathrm{O}}\)
ix. If \(\bar{a}, \bar{b}\) or \(\bar{c}\) are any three vectors then \(\bar{a}(\bar{b} \times \bar{c})+\bar{b} \times(\bar{c} \times \bar{a})+\bar{c} \times(\bar{a} \times \bar{b})\) are coplanar. [since sum of these vectors is zero]
x. \(\bar{a}(\bar{b} \times \bar{c})\) is vector lies in the plane of \(\bar{b}\) and \(\bar{c}\) or parallel to the plane of \(\bar{b}\) and \(\bar{c}\).

Product of Four Vectors:
Dot product of four vectors : The dot product of four vectors a̅, b̅, c̅ and d̅ is given as \((\bar{a} \times \bar{b}) \cdot(\bar{c} \times \bar{d})=(\bar{a} \cdot \bar{c})(\bar{b} \cdot \bar{d})-(\bar{a} \cdot \bar{d})(\bar{b} \cdot \bar{c})=\left|\begin{array}{ll}
\bar{a} \cdot \bar{c} & \bar{a} \cdot \bar{d} \\
\bar{b} \cdot \bar{c} & \bar{b} \cdot \bar{d}
\end{array}\right|\)
→ Cross product of four vectors : If a̅, b̅, c̅ and d̅ are any four vectors then
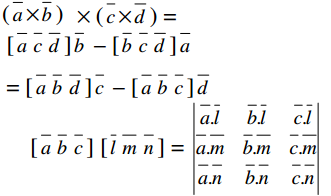
→ The vectorial equation of the plane passing through the point a and parallel to the vectors b̅, c̅is \([\overline{\mathrm{r}} \overline{\mathrm{b}} \overline{\mathrm{c}}]=[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]\)
→ The vectorial equation of the plane passing through the points a̅, b̅ and parallel to the vector c̅ is \([\overline{\mathrm{rb}} \overline{\mathrm{c}}]+[\overline{\mathrm{r}} \overline{\mathrm{c}} \overline{\mathrm{a}}]=[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]\)
→ The vectorial equation of the plane passing through the points a̅, b̅, c̅ is \([\overline{\mathrm{r}} \overline{\mathrm{b}} \overline{\mathrm{c}}]+[\overline{\mathrm{r}} \overline{\mathrm{c}} \overline{\mathrm{a}}]+[\overline{\mathrm{ra}} \overline{\mathrm{b}}]=[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]\)
→ If the points with the position vectorsa̅, b̅, c̅, d̅ are coplanar, then the condition is \([\overline{\mathrm{a}} \overline{\mathrm{bd}}]+[\overline{\mathrm{b}} \overline{\mathrm{c}} \overline{\mathrm{d}}]+[\overline{\mathrm{c}} \overline{\mathrm{a}} \overline{\mathrm{d}}]=[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]\)

→ Length of the perpendicular from the origin to the plane passing through the points a̅, b̅, c̅ is \(\frac{|[\overline{\mathrm{a} b} \overline{\mathrm{c}}]|}{|\overline{\mathrm{b}} \times \overline{\mathrm{c}}+\overline{\mathrm{c}} \times \overline{\mathrm{a}}+\overline{\mathrm{a}} \times \overline{\mathrm{b}}|}\)
→ Length of the perpendicular from the point c̅ on to the line joining the points a̅, b̅ is \(\frac{\mid(\overline{\mathrm{a}}-\overline{\mathrm{c}}) \times(\overline{\mathrm{c}}-\overline{\mathrm{b}})}{|\overline{\mathrm{a}}-\overline{\mathrm{b}}|}\)
→ P, Q, R are non collinear points. Then distance of P to the plane OQR is OP. \(\left|\frac{\overline{\mathrm{OP}} \cdot(\overline{\mathrm{OQ}} \times \overline{\mathrm{OR}})}{|\overline{\mathrm{OQ}} \times \overline{\mathrm{OR}}|}\right|\)
→ Perpendicular distance from P(α̅ ) to the plane passing through A(a̅) and parallel to the vectors b and c is
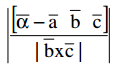
→ Length of the perpendicular from the point c̅ to the line \(\overline{\mathrm{r}}=\overline{\mathrm{a}}+\mathrm{tb}\) is \(\frac{|(\overline{\mathrm{c}}-\overline{\mathrm{a}}) \times \overline{\mathrm{b}}|}{|\overline{\mathrm{b}}|}\)

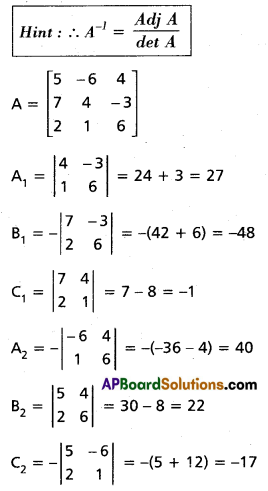



![]()





![]()
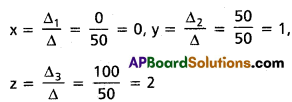


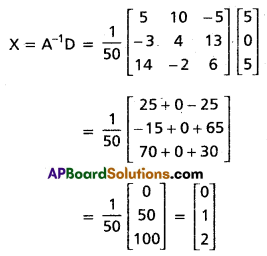

![]()

![]()
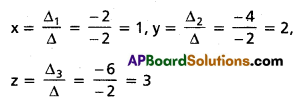



![]()




![]()




![]()