Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(b) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(b)
I.
Question 1.
Find the following products wherever possible.
Hint: (1 × 3) by (3 × 1) = 1 × 1
(i) \(\left[\begin{array}{lll}
-1 & 4 & 2
\end{array}\right]\left[\begin{array}{l}
5 \\
1 \\
3
\end{array}\right]\)
(ii) \(\left[\begin{array}{ccc}
2 & 1 & 4 \\
6 & -2 & 3
\end{array}\right]\left[\begin{array}{l}
1 \\
2 \\
1
\end{array}\right]\)
(iii) \(\left[\begin{array}{cc}
3 & -2 \\
1 & 6
\end{array}\right]\left[\begin{array}{cc}
4 & -1 \\
2 & 5
\end{array}\right]\)
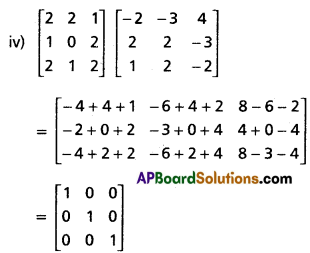
(iv) \(\left[\begin{array}{lll}
2 & 2 & 1 \\
1 & 0 & 2 \\
2 & 1 & 2
\end{array}\right]\left[\begin{array}{ccc}
-2 & -3 & 4 \\
2 & 2 & -3 \\
1 & 2 & -2
\end{array}\right]\)
(v) \(\left[\begin{array}{ccc}
3 & 4 & 9 \\
0 & -1 & 5 \\
2 & 6 & 12
\end{array}\right]\left[\begin{array}{ccc}
13 & -2 & 0 \\
0 & 4 & 1
\end{array}\right]\)
(vi) \(\left[\begin{array}{c}
1 \\
-2 \\
1
\end{array}\right]\left[\begin{array}{ccc}
2 & 1 & 4 \\
6 & -2 & 3
\end{array}\right]\)
(vii) \(\left[\begin{array}{cc}
1 & -1 \\
-1 & 1
\end{array}\right]\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
(viii) \(\left[\begin{array}{ccc}
0 & c & -b \\
-c & 0 & a \\
b & -a & 0
\end{array}\right]\left[\begin{array}{ccc}
a^{2} & a b & a c \\
a b & b^{2} & b c \\
a c & b c & c^{2}
\end{array}\right]\)
Solution:
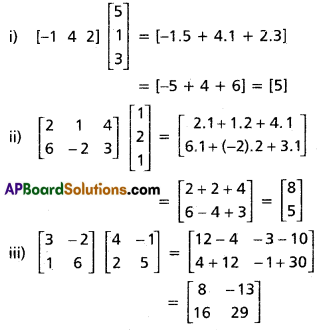
(v) \(\left[\begin{array}{ccc}
3 & 4 & 9 \\
0 & -1 & 5 \\
2 & 6 & 12
\end{array}\right]\left[\begin{array}{ccc}
13 & -2 & 0 \\
0 & 4 & 1
\end{array}\right]\)
First matrix is a 3 × 3 matrix and second matrix is 2 × 3 matrix.
No. of columns in the first matrix ≠ No. of rows in the second matrix.
∴ Matrix product is not possible.
![]()
(vi) \(\left[\begin{array}{c}
1 \\
-2 \\
1
\end{array}\right]\left[\begin{array}{ccc}
2 & 1 & 4 \\
6 & -2 & 3
\end{array}\right]\)
No. of columns in first matrix = 1
No. of rows in second matrix = 2
No. of columns in the first matrix ≠ No. of rows in the second matrix
Multiplication of matrices is not possible.

Question 2.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
-4 & 2 & 5
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
2 & 3 \\
4 & 5 \\
2 & 1
\end{array}\right]\), do AB and BA exist? If they exist, find them. Do A and B commute with respect to multiplication?
Solution:

AB ≠ BA
∴ A and B are not commutative with respect to the multiplication of matrices.
![]()
Question 3.
Find A2 where A = \(\left[\begin{array}{cc}
4 & 2 \\
-1 & 1
\end{array}\right]\)
Solution:

Question 4.
If A = \(\left[\begin{array}{ll}
i & 0 \\
0 & i
\end{array}\right]\), find A2.
Solution:

Question 5.
If A = \(\left[\begin{array}{cc}
i & 0 \\
0 & -i
\end{array}\right]\), B = \(\left[\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right]\) and C = \(\left[\begin{array}{ll}
0 & \mathbf{i} \\
\mathbf{i} & \mathbf{0}
\end{array}\right]\), and I is the unit matrix of order 2, then show that
(i) A2 = B2 = C2 = -I
(ii) AB = -BA = -C
Solution:

Question 6.
If A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
3 & 2 & 0 \\
1 & 0 & 4
\end{array}\right]\), find AB. Find BA if it exists.
Solution:
Given A = \(\left[\begin{array}{ll}
2 & 1 \\
1 & 3
\end{array}\right]\) and B = \(\left[\begin{array}{lll}
3 & 2 & 0 \\
1 & 0 & 4
\end{array}\right]\)
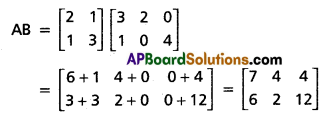
The order of AB is 2 × 3
BA does not exist since no. of columns in B ≠ No. of rows in A.
![]()
Question 7.
If A = \(\left[\begin{array}{cc}
2 & 4 \\
-1 & k
\end{array}\right]\) and A2 = 0, then find the value of k.
Solution:
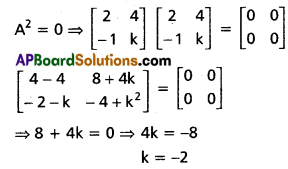
II.
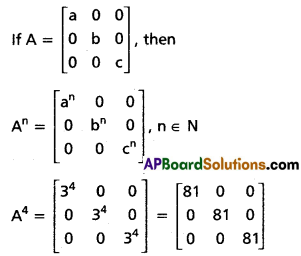
Question 1.
If A = \(\left[\begin{array}{lll}
3 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 3
\end{array}\right]\) then find A4.
Solution:
Question 2.
If A = \(\left[\begin{array}{ccc}
1 & 1 & 3 \\
5 & 2 & 6 \\
-2 & -1 & -3
\end{array}\right]\) then find A3.
Solution:


Question 3.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 1 \\
0 & 1 & -1 \\
3 & -1 & 1
\end{array}\right]\), then find A3 – 3A2 – A – 3I, where I is unit matrix of order 3 × 3.
Solution:


Question 4.
If I = \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) and E = \(\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\), show that (aI + bE)3 = a3I + 3a2bE, Where I is unit matrix of order 2.
Solution:

![]()
III.
Question 1.
If A = [a1, a2, a3,], then for any integer n ≥ 1 show that An = \(\left[\begin{array}{lll}
a_{1}, & a_{2}^{n}, & a_{3}^{n}
\end{array}\right]\)
Solution:
Given A = diag [a1, a2, a3,] = \(\left[\begin{array}{ccc}
a_{1} & 0 & 0 \\
0 & a_{2} & 0 \\
0 & 0 & a_{3}
\end{array}\right]\)
An = diag \(\left[\begin{array}{lll}
a_{1}^{n} & a_{2}^{n} & a_{3}^{n}
\end{array}\right]=\left[\begin{array}{ccc}
a_{1}^{n} & 0 & 0 \\
0 & a_{2}^{n} & 0 \\
0 & 0 & a_{3}^{n}
\end{array}\right]\)
This problem can be should by using Mathematical Induction
put n = 1
A1 = \(\left[\begin{array}{ccc}
a_{1} & 0 & 0 \\
0 & a_{2} & 0 \\
0 & 0 & a_{3}
\end{array}\right]\)
∴ The result is true for n = 1
Assume the result is true for n = k
Ak = \(\left[\begin{array}{ccc}
a_{1}^{k} & 0 & 0 \\
0 & a_{2}^{k} & 0 \\
0 & 0 & a_{3}^{k}
\end{array}\right]\)
Consider

∴ The result is true for n = k + 1
Hence by the Principle of Mathematical Induction, the statement is true ∀ n ∈ N
Question 2.
If θ – φ = \(\frac{\pi}{2}\), then show that \(\left[\begin{array}{cc}
\cos ^{2} \theta & \cos \theta \sin \theta \\
\cos \theta \sin \theta & \sin ^{2} \dot{\theta}
\end{array}\right]\) \(\left[\begin{array}{cc}
\cos ^{2} \phi & \cos \phi \sin \phi \\
\cos \phi \sin \phi & \sin ^{2} \phi
\end{array}\right]\) = 0
Solution:


Question 3.
If A = \(\left[\begin{array}{rr}
3 & -4 \\
1 & -1
\end{array}\right]\) then show that An = \(\left[\begin{array}{cc}
1+2 n & -4 n \\
n & 1-2 n
\end{array}\right]\), for any integer n ≥ 1 by using Mathematical Induction.
Solution:
We shall prove the result by Mathematical Induction.

∴ The given result is true for n = k + 1
By Mathematical Induction, the given result is true for all positive integral values of n.
![]()
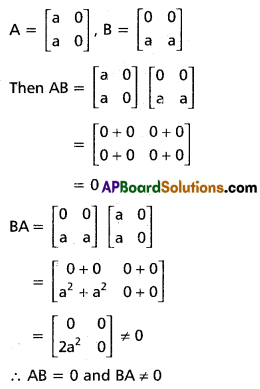
Question 4.
Give examples of two square matrices A and B of the same order for which AB = 0 but BA ≠ 0.
Solution:
Question 5.
A Trust fund has to invest ₹ 30,000 in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication, determine how to divide ₹ 30,000 among the two types of bonds if the trust fund must obtain an annual total interest of (a) ₹ 1800 (b) ₹ 2000
Solution:
Let the first bond be ‘x’ and the second bond be 30,000 – x respectively
The rate of interest is 0.05 and 0.07 respectively.
(a) \([x, 30,000-x]\left[\begin{array}{l}
0.05 \\
0.07
\end{array}\right] \quad=[1800]\)
[0.05x + 0.07(30,000 – x)] = 1800
\(\frac{5}{100} x+\frac{7}{100}(30,000-x)=1800\)
5x + 21,0000 – 7x = 1,80,000
-2x = 1,80,000 – 2,10,000 = -30,000
x = 15,000
∴ First bond = 15,000
Second bond = 30,000 – 15,000 = 15,000
![]()
(b) \(\left[\begin{array}{ll}
x & 30,000-x
\end{array}\right]\left[\begin{array}{l}
0.05 \\
0.07
\end{array}\right]=[2000]\)
[0.05x + 0.07(30,000 – x)] = [2000]
\(\frac{5 x}{100} \times \frac{7}{100}(30,000-x)=2000\)
5x + 2,10,000 – 7x = 2,00,000
-2x = 2,00,000 – 2,10,000
-2x = -10,000
x = 5,000
∴ First bond = 5000
Second bond = 30,000 – 5000 = 25,000