AP Inter 2nd Year Physics Model Paper Set 3 with Solutions

Thoroughly analyzing AP Inter 2nd Year Physics Model Papers Set 3 helps students identify their strengths and weaknesses.

AP Inter 2nd Year Physics Model Paper Set 3 with Solutions

Time: 3 Hours
Maximum Marks: 60

Section – A

Answer all questions. Each carries two marks. (10 × 2 = 20 Marks)

Question 1.
What is the principle of superposition of waves ?
Answer:
When two or more waves are acting simultaneously on the particle of the medium, the resultant displacement is equal to the algebraic sum of individual displacements of all the waves. This is the principle of superposition of waves.
If y₁, y₂, …. y_n be the individual displacements of the
particles,then resultant displacement y = y₁ + y₂ + …… + y_n.

Question 2.
A small angled prism of 4° deviates a ray through 2.48°. Find the refractive index of the prism.
Answer:
A = 4°, D_m = 2.48°
D_m = A (μ – 1)
μ – 1 = \(\frac{\mathrm{D}_{\mathrm{m}}}{\mathrm{A}}=\frac{2.48}{4}\) = 0.62
μ = 1 + 0.62, p = 1.62

Question 3.
State Gauss law is electrostatics ?
Answer:
Gauss’s law: It states that “the total electric flux through any closed surface is equal to \(\frac{1}{\varepsilon_0}\) times net charge enclosed by the surface”.
\(\int_S \vec{E} \cdot \overrightarrow{d s}=\frac{q}{\epsilon_0}=\frac{q}{\varepsilon_0}\)

Question 4.
What happens to the capacitance of a parallel plate capacitor, if the area of its plate is doubled ?
Answer:
\(\frac{\mathrm{C}_2}{\mathrm{C}_1}=\frac{\mathrm{A}_2}{\mathrm{~A}_1}\) [∵ C = \(\frac{\varepsilon_0 A}{d}\)]
Given A₂ = 2A, = \(\frac{\mathrm{C}_2}{\mathrm{C}_1}=\frac{2 \mathrm{~A}_1}{\mathrm{~A}_1}\) ∴ C₂ = 2C₁
Therefore capacity increases by twice.

Question 5.
Why are household appliances connected in parallel ?
Answer:
In parallel, the voltage (V) across each appliance is same. The current (I) through them depends upon the power (P) of the appliance. The higher power appliance draws more current and lower power appliance draws less current.
(∵ P = VI or I ∝ P)

Question 6.
State Ampere’s law and Biot-savart’s law.
Answer:
Ampere’s law : The line integral of the intensity of magnetic induction around a closed path is equal to μ times the total current enclosed in it.
∴ \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} l}\) = μ₀ i.
Biot – Savart’s laws : Biot – Savart’s states that the intensity of magnetic induction (dB) due to a small element is directly proportional to the

1. current (i)
2. length of the element (dl)
3. sine angle between radius vector (r) and dl and
4. Inversely proportional to the square of the point from current element.

∴ dB ∝.\(\frac{\mathrm{i} \mathrm{d} l \sin \theta}{\mathrm{r}^2}\)
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)

Question 7.
What are Eddy currents ?
Answer:
Eddy currents (or) Foucault currents : The induced circulating currents produced in a conductor itself due to change in magnetic flux linked with the conductor are called Eddy currents.
Due to Eddy currents, the energy is dissipated in the form of heat energy.

Question 8.
A transformer converts 200 V a.c into 2000 V.a.c. calculate the number of turns in the secondary if the primary has 10 turns.
Answer:
\(\frac{V_S}{V_p}=\frac{N_s}{N_p}\)
V_p = 200V, V_s = 2000V, N_p = 10
N_s = \(\frac{V_s}{V_p}\) × N_p = \(\frac{2000}{200}\) × 100
N_s = 100.

Question 9.
What is work function ?
Answer:
The minimum energy required to liberate an electron from photometal surface is called work function, Φ₀.

Question 10.
What is the function of moderator in a nuclear reactor ?
Answer:
They are used to slow down the fast moving neutrons produced during the fission process. .
e.g. : Heavy water, Berilium.

Section – B

Answer any six questions. Each carries four marks. (6 × 4 = 24 Marks)

Question 11.
With a neat labelled diagram, explain the formation of image in a simple microscope.
Answer:
Simple microscope : It consists a single short focus convex lens. It increases the visual angle to see an object clearly. It is also called magnifying glass (or) reading glass.

Working : The object is adjusted within the principal focus of the convex lens to form the image at the near point. The image is formed on same side of the object and it is virtual, erect and magnified as shown in fig.

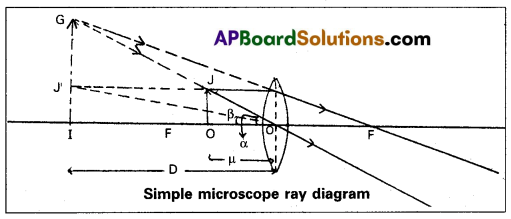
Magnifying power : The ratio of the angle subtended by the image at the eye to the angle subtended by the object at the eye is called magnifying power of a simple microscope.
It is denoted by ‘m’
m = \(\frac{\alpha}{\beta} \simeq \frac{{Tan} \alpha}{{Tan} \beta}\)

Question 12.
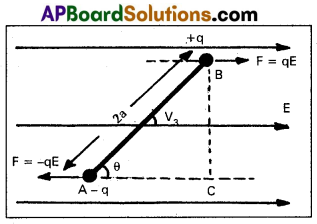
Derive an expression for the potential energy of an electric dipole placed in a uniform electric field.
Answer:
Expression for potential energy of an electric dipole placed in a uniform electric field :
1) Consider a electric dipole of length 2a having charges + q and -q.

2) The electric dipole is placed in uniform electric field E and it’s axis makes an angle θ with E.

3) Force on charges are equal but opposite sign. They constitute torque on the dipole.
Torque τ = one of its force (F) × ⊥^r distance (BC)
F = qE and sinθ = \(\frac{B C}{2 a}\) ⇒ Be = 2a sinθ
∴ Torque τ = qE × 2a sinθ = PE sin θ = [∴ p = 2aq]

4) Suppose the dipole is rotated through an angle dθ, the workdone dw is given by
dw = τdθ = PE sinθ dθ

5) For rotating the dipole from angle θ₁ to θ₂,
workdone W = \(\int_{\theta_1}^{\theta_2} \mathrm{PE} \sin \theta \mathrm{d} \theta=\mathrm{PE}\left(\cos \theta_1-\cos \theta_2\right)\)

6) This workdone (W) is then stored as potential energy(U) in the dipole.
∴ U = PE(cosθ₁ – cosθ₂)

7) If θ₁ = 90° and θ₂ = 0°, U = – PE cos0.
In vector form U = – P.E

Question 13.
State the working principle of potentiometer. Explain with the help of circuit diagram. How the e.m.f of two primary cells are compared by using the potentiometer.
Answer:
Working principle of potentiometer : The potential difference across a length of the potentiometer wire is directly proportional to its length (or) when a steady current is passed through a uniform wire, potential drop per unit length or potential gradient is constant,
i.e. ε ∝ l ⇒ ε = Φl where Φ is potential gradient.

Comparing of emf of two cells ε₁ and ε₂ :
1) To compare the emf of two cells of emf E₁ and E₂ with potentiometer is shown in diagram.

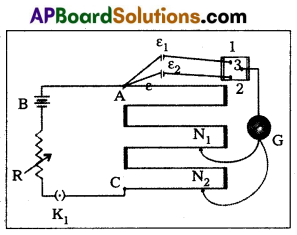
2) The points marked 1, 2, 3 form a two way key.
3) Consider first a position of the key where 1 and 3 are connected so that the galvanometer is connected to ε₁.
4) The Jockey is moved along the wire till at a point N₁ at a distance l₁ from A, there is no deflection in the galvanometer.
Then ε₁ ∝ l₁ ⇒ ε₁ = Φl₁ (1)
5) Similarly, if another emf e2 is balanced against
l₂ (AN₂), then ε₂ ∝ l₂ ⇒ Φl₂ (2)
6) \(\frac{(1)}{(2)} \Rightarrow \frac{\varepsilon_1}{\varepsilon_2}=\frac{l_1}{l_2}\)

Question 14.
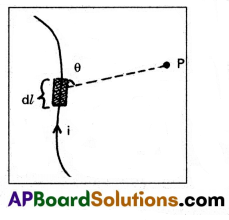
State and explain Biot – Savart’s law.
Answer:
Consider a very small element of length dl of a conductor carrying current (i). Magnetic induction due to small element at a point p distance r form the element.

‘Magnetic induction (dB) is directly proportional to i) current (i) ii) Length of the element (dl) iii) sine angle between r and d/and iv) Inversely proportional to the square of the distance from small element to point P.
dB ∝ \(\frac{\mathrm{i} \mathrm{d} l \sin \theta}{\mathrm{r}^2}\)
dB = \(\frac{\mu_0}{4 \pi} \cdot \frac{\mathrm{id} l \sin \theta}{\mathrm{r}^2}\)
where μ⁰ = permeability in free space.
\(\frac{\mu_0}{4 \pi}\) = 10^-7 Wb m^-1A^-1
In vector form \(\overrightarrow{\mathrm{dB}}=\frac{\mu_0 \mathrm{i}}{4 \pi} \frac{(\overrightarrow{\mathrm{d} l} \times \overrightarrow{\mathrm{r}})}{\mathrm{r}^3}\)

Question 15.
Obtain Gauss law for magnetism and explain it.
Answer:
Gauss law for Magnetism :

1. According to Gauss’s law for. magnetism, the net magnetic flux (Φ_B) through any closed surface is always zero.
2. The law implies that the no. of magnetic field lines leaving any closed surface is always equal to the number of magnetic field lines entering it.
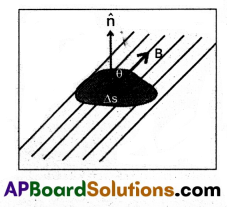
3. Suppose a closed surface S is held in a uniform magnetic field B. Consider a small vector area element ΔS of this surface as shown in figure.
4. Magnetic flux through this area element is defined as ΔΦ_B = B. ΔS.
   Then the net flux Φ_B, is,
   \(\phi_B=\sum_{\text {all }} \Delta \phi_B=\sum_{\text {all }} B \cdot \Delta S\)
5. If the area elements are really small, we can rewrite this equation as
   \(\phi_{\mathrm{B}}=\oint \mathrm{B} \cdot \mathrm{ds}=0\) = 0 …….. (I)
6. Comparing this equation with Gauss’s law of electrostatics i.e., electric flux through a closed surface S is given by
   \(\phi_{\mathrm{E}}=\oint \mathrm{E} \cdot \Delta \mathrm{S}=\frac{\mathrm{q}}{\varepsilon_0}\) ……. (II).
   Where q is the electric charge enclosed by the surface.
7. In an electric dipole were enclosed by the surface equal and opposite charges in the dipole add upto zero. Therefore, Φ_E would be zero.
8. The fact that Φ_B = 0 indicates that the simplest magnetic element is a dipole or current loop.
9. The isolated magnetic poles, called magnetic monopoles are not known to exist.
10. All magnetic phenomena can be explained interms of an arrangement of magnetic dipoles and /or current loops.
11. Thus corresponding to equation (II) of Gauss’s theorem in electrostatics, we can visualize equation (I) as
    \(\phi_{\mathbf{B}}=\int_{\mathrm{S}} \mathrm{B} \cdot \mathrm{dS}=\mu_0(\mathrm{~m})+\mu_0(-\mathrm{m})=0\) where m is strength of N-pole and-m is strength of S – pole of same magnet.
12. The net magnetic flux through any closed surface is zero.

Question 16.
Describe the ways in which Eddy currents are used to advantage.
Answer:
Eddy Currents are used-to advantage in
i) Magnetic braking in trains : A strong magnetic field is applied across the metallic drum rotating with the axle of the electric train. Thus large eddy currents are produced in the metallic drum. These currents oppose the motion of the drum and hence the axle of the train which ultimately makes the train come to rest.

ii) Induction Motor : Eddy currents are used to rotate the short circuited rotor of an induction motor. Ceiling fans are also induction motors which run on single phase alternating current.

iii) Electromagnetic damping: Certain galvanometers have a fixed core made of non magnetic metallic material. When the coil oscillates, the eddy currents generated in the core oppose the motion and bring the coil to rest quickly.

iv) Induction furnace : Induction furnace can be used to produce high temperatures and can be utilised to prepare alloys, by melting the constituent metals. A high frequency alternating current is passed through a coil. The eddy currents generated in the metals produce high temperatures sufficient to melt it.

v) Analogue energy meters : Concept of eddy currents is used in energy meters to record the consumption of electricity. Aluminium disc used in these meters get induced due to varying magnetic field. It rotates due to eddy currents produced in it.

Question 17.
Obtain an expression for the current in a capacitor when an A.C e.m.f is applied.
Answer:
Circuit consists of pure capacitor of capacitance C. Let an A.C emf V = V_m sin ωt is applied to it. Let i and q be the instantaneous values of current and charge.
Potential difference across capacitor = – \(\frac{\mathrm{q}}{\mathrm{C}}\)
Total emf = V₀ sin ωt –\(\frac{\mathrm{q}}{\mathrm{C}}\)
According to Ohms law this must be equal to iR = 0.
V₀ sin ωt –\(\frac{\mathrm{q}}{\mathrm{C}}\) = 0
\(\frac{\mathrm{q}}{\mathrm{C}}\) = V_msin ωt ……….. (1)
q = V_m C sinωt
Differentiating w.r.to time
\(\frac{\mathrm{dq}}{\mathrm{dt}}\) = V_m ωC cos ωt [∵ i = \(\frac{\mathrm{dq}}{\mathrm{dt}}\)] ………… (2)
i = \(\frac{V_m}{1 / \omega C}\) sin (ωt + \(\frac{\pi}{2}\)) (∵ i₀ = \(\frac{\mathrm{V}_{\mathrm{m}}}{1 \omega \mathrm{C}}\))
i = i₀sin (ωt + \(\frac{\pi}{2}\)) ……….. (3)
i₀ is peak value of current. Here the current leads the applied e.m.f
by \(\frac{\pi}{2}\) radian (or) 90°.

Question 18.
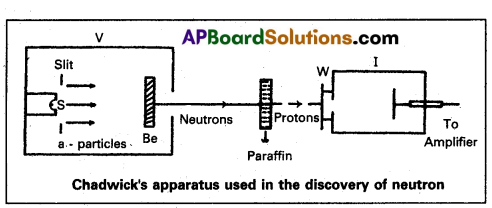
Write a short note on the discovery of neutron.
Answer:
1) Bothe and Becker found that when beryllium is bombarded with α – particles of energy 5 MeV, which emitted a highly penetrating radiation.

2) The equation for above process can be written as \({ }_4^9 \mathrm{Be}\) + \({ }_2^4 \mathrm{He}\) → \({ }_6^13 \mathrm{C}\) + γ – (radiation energy.

3) The radiations are not effected by electric and magnetic fields.

4) In 1932, James Chadwick, had subjected nitrogen and argon to the beryllium radiation. He interpreted the experimental results by assuming that the radiation is of a new kind of particles which has no charge and its mass is equal to proton. These neutral particles were named as ‘neutrons’. Thus the neutron was discovered.

5) The experimental results can be represented by the following equation.
\({ }_4^9 \mathrm{Be}\) + \({ }_2^4 \mathrm{He}\) → \({ }_6^12 \mathrm{C}\) + \({ }_0^1 \mathrm{n}\) + Q

Section – C

Answer any two of the following. Each carries 8 marks. (2 × 8 = 16 Marks)

Question 19.
What is Doppler effect ? Obtain an .expression for the apparent frequency of sound heard, when the source is in motion with respect to an observer at rest.
A train sounds in whistle as it approaches and crosses a level crossing. An observer at the crossing measures a frequency of 219 Hz as it leaves. If the speed of sound is taken to be 340m/s, find the speed of the train and the frequency of its whistle.
Answer:
Doppler effect : The apparent change in the frequency heard by the observer due to the relative motion between the observer and the source of sound is called doppler effect.

When a whistling railway engine approaches an observer standing on the platform, the frequency of sound appears to increase. When it moves away the frequency appear to decrease.

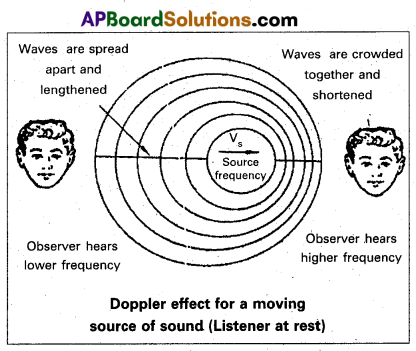
Expression for apparént frequency when source is in motion and listener at rest:
Let S = Source of sound
O = Listener
Let ‘S’ be the source, moving with a velocity ‘υ_s‘ towards the stationary listener.
The distance travelled by the source in time period ‘T’ = υ_s. T
Therefore the successive compressions and rarefactions are drawn closer to listener.
∴ Apparent wavelength λ’ = λ – υ_ST.
λ’ = λ – \(\frac{υ_{\mathrm{s}}}{\mathrm{n}}\) [∵ n = \(\frac{1}{\mathrm{~T}}\)]
= \(\frac{\lambda υ-υ_s}{υ}=\frac{υ-υ_s}{υ}\) [∵ υ = vλ]
If “v’ ” is apparent frequency heard by the listener then v’ = \(\frac{υ}{\lambda^{\prime}}\) where ‘υ’ is velocity of sound in air
v’ = \(\frac{υ . υ}{υ-υ_s}\)
Therefore the apparent frequency is greater than the actual frequency.

Note : If the source is away from the stationary listener then apparent frequency v’ = \(\frac{υ . υ}{υ-υ_s}\), which is less than the actual frequency.

Limitation : Doppler effect is applicable when the velocities of the source and listener are much less than that of sound velocity.

Solution:
When a whistling train approaches to rest observer,
v’ [latex]\frac{υ}{υ-υ_s}[/latex] v …… (1)
When a whistling train away from rest observer,
v’ [latex]\frac{υ}{υ+υ_s}[/latex] v …… (2)
Here v’ = 219 Hz; v” = 184 Hz;
v = 340 m/s
\(\frac{(1)}{(2)} \Rightarrow \frac{v^{\prime}}{v^{\prime \prime}}=\frac{\left(υ+υ_s\right)}{\left(υ-υ_2\right)}\)
\(\frac{219}{184}=\frac{340+υ_s}{340-υ_s}\)
219(340 – υ_s = 184(340 + υ_s)
219 × 340 – 219 υ_s – 184 × 340 + 184 υ_s
403 υ_s = 35 × 340
∴ Velocity of train υ_s = 29.5 m/s
Frequency of whistle, v = v’ × \(\frac{υ-υ_s}{υ}\)
219 × \(\frac{340-29.5}{340}\)
= 199.98
∴ v = 200 Hz.

Question 20.
Outline the path breaking experiments of Faraday and Henry and highlight the contributions of these experiments to our understanding of electromagnetism.
Answer:
Faraday’s and Henry’s experiments:

Experiment 1 : A magnet induces current due to relative motion

• The apparatus consists of a coil with a galvanometer G and a bar magnet.

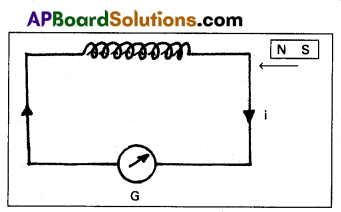
• When the bar magnet (NS) was at rest, the galvanometer shows no deflection.
• When North pole of the bar magnet moved towards the coil, galvanometer shows the deflection in one direction indicating the flow of current in the coil.
• When North pole of the bar magnet moved away from the coil, galvanometer again.showed the deflection but now in the opposite direction.
• The deflection of the galvanometer was large when the bar magnet was moved faster towards (or) away from the coil.
• When south pole of the magnet was brought near the coil (or) moved , away from the coil, the deflections in the galvanometer are opposite to that observed with the north pole for similar movements.

Conclusion:

• Whenever there is a relative motion between a coil and a magnet, induced current flows through the coil.
• Large induced e.m.f. (or) current is produced in the coil if the relative motion between magnet and the coil is large.

Experiment 2:
Current induces current due to relative motion of coils :

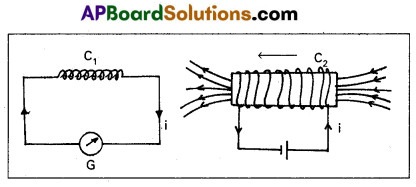
• The bar magnet is replaced by a secondary coil C₂ connected to a battery as shown in figure.
• The steady current in the coil C₂ produces a steady magnetic field.
• As coil c₂ is moved towards the coil C₁ the galvanometer shows a
  deflection. This indicates current is induced in the coil C₁
• When coil C₂ is moved away, the galvanometer shows a deflection again, but opposite direction.
• The deflection lasts as long as coil C₂ is in motion.
• When the coil C₂ is held fixed and C₁ is moved, the same effects are observed.

Conclusion : Induced e.m.f (or) current is produced, when there is a relative motion between the coils.

Experiment 3 : Changing current, induces current without relative motion :

• Faraday showed that this relative motion is not an absolute requirement.

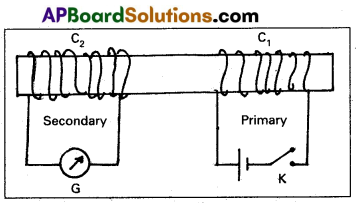
• Figure shows two coils C₁ and C₂ held stationary.
• Coil C₁ is connected to a battery through a tap key K arid coil C₂ is corinected to a galvanometer (G).
• It is observed that the galvanometer shows a momentary deflection when the tap key K is pressed.
• The pointer in the galvanometer returns to zero immediately.
• If the key is held pressed continuously, there is no deflection in the galvanometer.
• When the key is released, the galvanometer shows deflection again but in the opposite direction.
• Deflection of the galvanometer increases a lot when wooden bar is replaced by iron bar.

Question 21.
Discuss Bohr’s theory of the spectrum of hydrogen atom.
The radius of the first electron orbit of a hydrogen atom is 5.3 × 10^-11m. What is the radius of the second orbit ?
Answer:
1) According to Bohr’s model an electron continuous to revolve round the nucleus in fixed, stationary orbits. This is called ground ‘ state of the atom. In ground state there is no emission of radiation.

2) But when some energy is given to an atom the electron absorbs this energy. This is called excited state of the atom. In this state the electron jumps to the next higher orbit. But it can remain 12^-8 sec and it immediatly returns back to its ground state and the balance of the energy is emitted out as a spectral line.

3) According to Bohr’s third postulate, the emitted energy is given by E = hv = E₂ – E₁

Spectral series of Hydrogen atom:

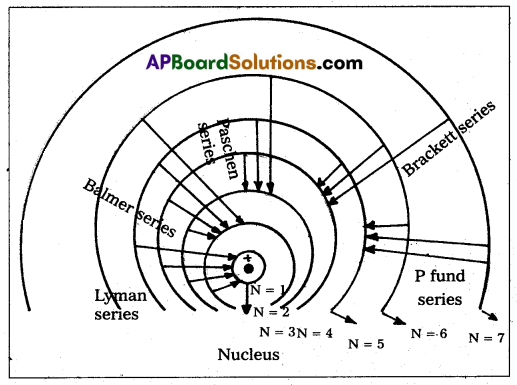
Hydrogen atom has five series bf spectral lines. They are
1. Lyman series : When an electron jumps from the outer orbits to the first orbit, the spectral lines are in the ultra – violet region. Here n₁ = 1, n₂ = 2, 3, 4, 5…. 2
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{1^2}-\frac{1}{\mathrm{n}_2^2}\right]=\mathrm{R}\left[1-\frac{1}{\mathrm{n}_2^2}\right]\)

2) Balmer Sertes : When an electron jumps from the outer orbits to the second orbit, the spectral lines are in the visible region.
Here n₁ = 2, n₂ = 3, 4, 5…
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{2^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

3) Paschen series : When an electron jumps from the outer orbits to the third orbit, the spectral lines are in the near infrared region.
Here n₁ = 3, n₂ = 4, 5, 6 ….
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{3^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

4) Brackett series : When an electron jumps from outer orbits to the forth orbit, the spectral lines are in the infrared region.
Here n₁ = 4, n₂ = 5, 6, 7 ….
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{4^2}-\frac{1}{\mathrm{n}_2^2}\right]\)

5) Pfund series : When an electron jumps from outer orbits to the fifth orbit, the spectral lines are in the far infrared region.
Here n₁ = 5, n₂ = 6, 7, 8, …..
\(\frac{1}{\lambda}=\mathrm{R}\left[\frac{1}{5^2}-\frac{1}{\mathrm{n}_2^2}\right]\)
Solution:
r_n ∝ n²
\(\frac{r_2}{r_1}=\frac{2^2}{1^2}=\frac{4}{1}\)
r₂ = 4r₁
∴ r₂ = 4 × 5.3 × 10^-11
= 2.12 × 10^-10 m