AP Inter 2nd Year Maths 2A Question Paper May 2017

Thoroughly analyzing AP Inter 2nd Year Maths 2A Model Papers and AP Inter 2nd Year Maths 2A Question Paper May 2017 helps students identify their strengths and weaknesses.

AP Inter 2nd Year Maths 2A Question Paper May 2017

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Attempt ALL the questions.
• Each question carries two marks.

Question 1.
Find the square roots of (-5 + 12i).
Solution:

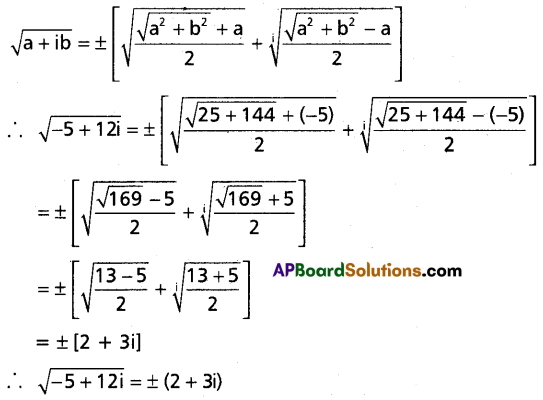
Question 2.
If Z₁ = -1 and Z₂ = -i, then find Arg (Z₁Z₂).
Solution:
Z₁ = -1
= 0 + i(-1)
= cos π + i sin π
∴ Arg Z₁ = π
Z₂ = -i
= 0 + i(-1)
= \(\cos \left(\frac{-\pi}{2}\right)+i \sin \left(\frac{-\pi}{2}\right)\)
∴ Arg Z₂ = \(\frac{-\pi}{2}\)
Arg (Z₁Z₂) = Arg Z₁ + Arg Z₂
= π + (\(\frac{-\pi}{2}\))
= π – \(\frac{\pi}{2}\)
= \(\frac{\pi}{2}\)

Question 3.
If x = cos θ, then find the value of \(\left(x^6+\frac{1}{x^6}\right)\).
Solution:
Given x = cis θ
⇒ x = cos θ + i sin θ
⇒ x⁶ = (cos θ + i sin θ)⁶
⇒ x⁶ = cos 6θ + i sin 6θ)
⇒ \(\frac{1}{x^6}=\frac{1}{\cos 6 \theta+i \sin 6 \theta}\)
⇒ \(\frac{1}{x^6}\) = cos 6θ – i sin 6θ
∴ x⁶ + \(\frac{1}{x^6}\) = cos 6θ + i sin 6θ + cos 6θ – i sin 6θ
∴ x⁶ + \(\frac{1}{x^6}\) = 2 cos 6θ

Question 4.
Find the values of m for which the equation x² – 15 – m(2x – 8) = 0 have equal roots.
Solution:
Given quadratic equation is x² – 15 – m(2x – 8) = 0
⇒ x² – 15 – 2mx + 8m = 0
⇒ x² – 2mx + (8m – 15) = 0
Since it has equal roots
∴ (-2m)² – 4 . 1 (8m – 15) = 0
⇒ 4m² – 32m + 60 = 0
⇒ m² – 8m + 15 = 0
⇒ m² – 3m – 5m + 15 = 0
⇒ m(m – 3) – 5(m – 3) = 0
⇒ (m – 3) (m – 5) = 0
⇒ m = 3, 5

Question 5.
If -1, 2, and α are the roots of 2x³ + x² – 7x – 6 = 0, then find α.
Solution:
Since -1, 2, α are the roots of 2x³ + x² – 7x – 6 = 0.
S₁ = \(\frac{-1}{2}\)
⇒ -1 + 2 + α = \(\frac{-1}{2}\)
⇒ 1 + α = \(\frac{-1}{2}\)
⇒ α = \(\frac{-1}{2}\) – 1
⇒ α = \(\frac{-3}{2}\)

Question 6.
If ⁿP₇ = 42 . ⁿP₅, find n.
Solution:
Given ⁿP₇ = 42 . ⁿP₅
⇒ n(n – 1) (n – 2) (n – 3) (n – 4) (n – 5) (n – 6) = 42 . n(n – 1) (n – 2) (n – 3) (n – 4)
⇒ (n – 5) (n – 6) = 42
⇒ (n – 5) (n – 6) = 7 × 6
⇒ n – 5 = 7
⇒ n = 12

Question 7.
If ¹⁷C_2t+1 = ¹⁷C_3t-5, find t.
Solution:
Given ¹⁷C_2t+1 = ¹⁷C_3t-5
∴ 2t + 1 = 3t – 5 (or) 17 = 2t + 1 + 3t- 5
⇒ 1 + 5 = 3t – 2t (or) 17 = 5t – 4
⇒ t = 6 (or) 17 + 4 = 5t
⇒ t = 6 (or) t = \(\frac{21}{5}\)
since t is an integer
∴ t = 6

Question 8.
Find the number of terms in the expansion of (2x + 3y + z)⁷.
Solution:
The number of terms in the expansion of (2x + 3y + z)⁷ = \(\frac{(7+1)(7+2)}{2}\) = 36

Question 9.
Find the mean deviation from the mean of the following discrete data:
6, 7, 10, 12, 13, 4, 12, 16
Solution:
Given data 6, 7, 10, 12, 13, 4, 12, 16
Mean = \(\frac{6+7+10+12+13+4+12+16}{8}=\frac{80}{8}\) = 10
Absolute values about mean = |6 – 10|, |7 – 10|, |10 – 10|, |12 – 10|, |13 – 10|, |4 – 10|, |12 – 10|, |16 – 10| = 4, 3, 0, 2, 3, 6, 2, 6
∴ Mean deviation = \(\frac{4+3+0+2+3+6+2+6}{8}=\frac{26}{8}\) = 3.25

Question 10.
The mean and variance of a binomial distribution are 4 and 3 respectively. Fix the distribution and find P(X ≥ 1).
Solution:
Given mean = 4 ⇒ np = 4
variance = 3 ⇒ npq = 3
\(\frac{n p q}{n p}=\frac{3}{4}\)
⇒ q = \(\frac{3}{4}\)
∴ p = 1 – q
= 1 – \(\frac{3}{4}\)
= \(\frac{1}{4}\)
∴ n(\(\frac{1}{4}\)) = 4
⇒ n = 16
p(x ≥ 1) = 1 – p(x = 0)
= 1 – \(16_{c_o}\left(\frac{1}{4}\right)^0\left(\frac{3}{4}\right)^{16-0}\)
= 1 – \(\left(\frac{3}{4}\right)^{16}\)

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Answer any five questions.
• Each question carries four marks.

Question 11.
If x + iy = \(\frac{1}{1+\cos \theta+i \sin \theta}\), then show that 4x² – 1 = 0.

Question 12.
If x is real, prove that \(\frac{x}{x^2-5 x+9}\) lies between \(\frac{-1}{11}\) and 1.

Question 13.
If the letters of the word MASTER are permuted in all possible ways and the words thus formed are arranged in the dictionary order, then find the rank of the word MASTER.
Solution:
The alphabetical order of the letters of the word REMAST is A, E, M, R, S, T
The no.of words beginning with A is 5! = 120
The no.of words begin with E is 5! = 120
The no.of words begin with MAE is 3! = 6
The no.of words begin with MAR is 3! = 6
The no.of words begin with MASE is 2! = 2
The no.of words begin with MASR is 2! = 2
The next word is MASTER = 1
∴ Rank of the word MASTER = 120 + 120 + 6 + 6 + 2 + 2 + 1 = 257

Question 14.
Simplify: \({ }^{34} C_5+\sum_{r=0}^4(38-r) C_4\)
Solution:

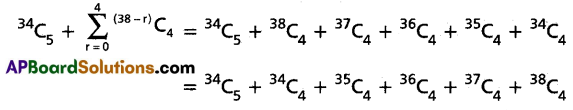
Question 15.
Resolve \(\frac{2 x^2+2 x+1}{x^3+x^2}\) into partial fractions.
Solution:

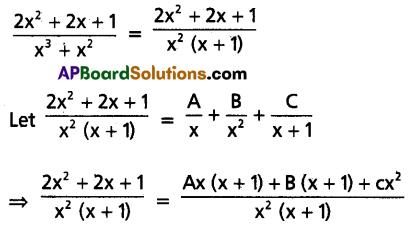
⇒ 2x² + 2x + 1 = Ax(x + 1) + B(x + 1) + Cx² …….(1)
Put x = 0 in (1)
⇒ 0 + 0 + 1 = 0 + B(0 + 1) + 0
⇒ B = 1
Put x = -1 in (1)
2(-1)² + 2(-1) + 1 = C(-1)²
⇒ 2 – 2 + 1 = C
⇒ C = 1
Comparing the coefficients of x² terms in (1)
2 = A + C
⇒ 2 = A + 1
⇒ A = 1
∴ A = 1, B = 1, C = 1
∴ \(\frac{2 x^2+2 x+1}{x^3+x^2}=\frac{1}{x}+\frac{1}{x^2}+\frac{1}{x+1}\)

Question 16.
State and prove the Addition theorem of Probability.

Question 17.
Suppose A and B are independent events with P(A) = 0.6, P(B) = 0.7, then compute
(i) P(A ∩ B)
(ii) P(A ∪ B)
(iii) P(\(\frac{B}{A}\))
(iv) P(Ac ∩ Bc)

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Attempt any five questions.
• Each question carries seven marks.

Question 18.
If α and β are the roots of the equation x² – 2x + 4 = 0, then for any n ∈ N. Show that \(\alpha^n+\beta^n=2^{n+1} \cos \left(\frac{n \pi}{3}\right)\).

Question 19.
Solve 8x³ – 36x² – 18x + 81 = 0, given that the roots of this equation are in arithmetic progression.
Solution:
Given 8x³ – 36x² – 18x + 81 = 0 ……..(1)
Let the roots of (1) be a – d, a, a + d
S₁ = \(\frac{-(-36)}{8}\)
⇒ a – d + a + a – d = \(\frac{36}{8}\)
⇒ 3a = \(\frac{36}{8}\)
⇒ a = \(\frac{3}{2}\)
∴ (x – \(\frac{3}{2}\)) is a factor of (1)

⇒ 8x² – 24x – 54 = 0
⇒ 4x² – 12x – 27 = 0
⇒ 4x² – 18x + 6x – 27 = 0
⇒ 2x(2x – 9) + 3(2x – 9) = 0
⇒ (2x + 3) (2x – 9) = 0
⇒ x = \(\frac{-3}{2}\), \(\frac{9}{2}\)
∴ Roots are \(\frac{-3}{2}\), \(\frac{3}{2}\), \(\frac{9}{2}\).

Question 20.
If n is a positive integer and x is any non-zero real number, then prove that \(C_0+C_1 \cdot \frac{x}{2}+C_2 \cdot \frac{x^2}{3}+C_3 \cdot \frac{x^3}{4}+\ldots . .+C_n \cdot \frac{x^n}{n+1}=\frac{(1+x)^{n+1}-1}{(n+1) x}\).

Question 21.
If x = \(\frac{1}{5}+\frac{1.3}{5.10}+\frac{1.3 .5}{5.10 .15}\) + …….. ∞, then find 3x² + 6x.

Question 22.
Find the mean deviation about the median for the following continuous distribution:

Age (Years)	20 – 25	25 – 30	30 – 35	35 – 40	40 – 45	45 – 50	50 – 55	55 – 60
No. of Workers (fi)	120	125	175	160	150	140	100	30

Solution:
Construct the table

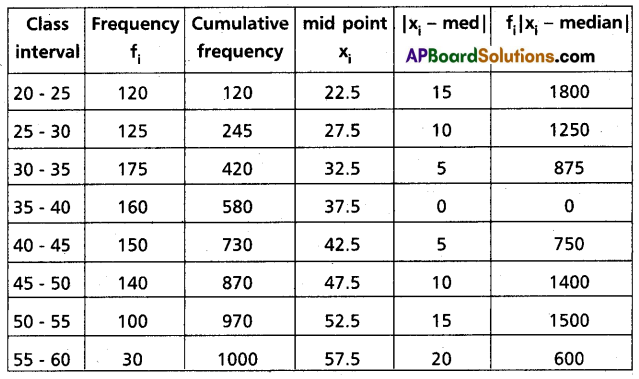
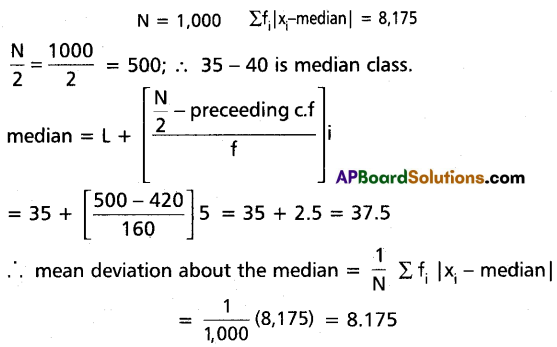
Question 23.
Suppose an urn B₁ contains 2 white and 3 black balls and another urn B₂ contains 3 white and 4 black balls. One urn is selected at random and a ball is drawn from it. If the ball drawn is found to be black, then find the probability that the urn chosen was B₁.
Solution:
Let E₁ and E₂ denote the events or selecting urns B₁ and B₂ respectively.
∴ P(E₁) = P(E₂) = \(\frac{1}{2}\)

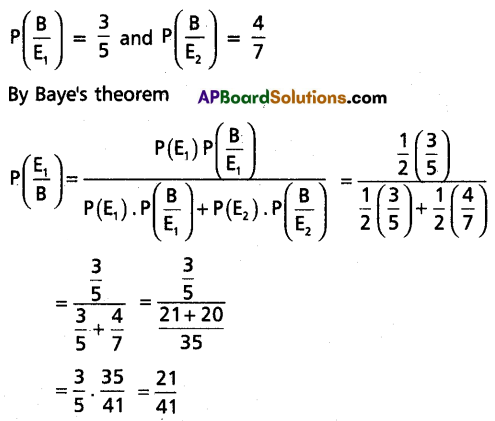
Question 24.
A random variable X has the following probability distribution:

X = x	0	1	2	3	4	5	6	7
P(X = x)	0	K	2K	2K	3K	K2	2K2	7K2 + K

Find (i) k, (ii) the mean, and (iii) P(0 < X < 5).