AP Inter 2nd Year Maths 2A Question Paper March 2018

Thoroughly analyzing AP Inter 2nd Year Maths 2A Model Papers and AP Inter 2nd Year Maths 2A Question Paper March 2018 helps students identify their strengths and weaknesses.

AP Inter 2nd Year Maths 2A Question Paper March 2018

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of THREE Sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer ALL questions.
• Each question carries TWO marks.

Question 1.
Find the complex conjugate of (2 + 5i) (-4 + 6i).
Solution:
Let Z = (2 + 5i) (-4 + 6i)
= -8 + 12i – 20i + 30i²
= -8 – 8i – 30 [∵ i² = -1]
= -38 – 8i
∴ \(\bar{Z}\) = -38 + 8i

Question 2.
If x + iy = cis α . cis β, then find the value of x² + y².
Solution:
Given x + iy = cis α . cis β
= cis(α + β)
= cos(α + β) + i sin(α + β)
Equating real and imaginary parts on bothsides
x = cos(α + β), y = sin(α + β)
∴ x² + y² = cos²(α + β) + sin²(α + β) = 1
∴ x² + y² = 1

Question 3.
If A, B, and C are angles of a triangle such that x = cis A, y = cis B, z = cis C, then find the value of XYZ.
Solution:
Since A, B, C are angles of a triangle.
∴ A + B + C = 180°
Given x = cis A, y = cis B, z = cis C
XYZ = (cis A) (cis B) (cis C)
= cis (A + B + C)
= cis 180°
= cos 180° + i sin 180°
= -1 + i(0)
= -1
∴ XYZ = -1

Question 4.
For what values of x the expression x² – 5x – 14 is positive?
Solution:
x² – 5x – 14 > 0
⇒ x² – 7x + 2x – 14 > 6
⇒ x(x – 7) + 2(x – 7) > 0
⇒ (x + 2) (x – 7) > 0
⇒ x < -2 (or) x > 7

Question 5.
If 1, 1, α are the roots of x³ – 6x² + 9x – 4 = 0, then find α.
Solution:
Since 1, 1, α are the roots of x³ – 6x² + 9x – 4 = 0
s₁ = \(\frac{-(-6)}{1}\)
⇒ 1 + 1 + α = 6
⇒ α = 6 – 2
⇒ α = 4

Question 6.
Find the number of ways of arranging the letter of the word “MATHEMATICS”.
Solution:
Given word MATHEMATICS contains 11 letters which 2M’S, 2A’S, 2T’S, and the rest are different.
∴ The number of ways of arranging the letters of the word MATHEMATICS = \(\frac{11 !}{2 ! 2 ! 2 !}=\frac{11 !}{(2 !)^3}\)

Question 7.
Find the value of ¹⁰C₅ + 2 . ¹⁰C₄ + ¹⁰C₃.
Solution:

Question 8.
Find the 8th term of \(\left(1-\frac{5 x}{2}\right)^{-3 / 5}\).
Solution:

Question 9.
Find the mean deviation about the mean for the following data:
3, 6, 10, 4, 9, 10
Solution:
Given data 3, 6, 10, 4, 9, 10
Mean = \(\frac{3+6+10+4+9+10}{6}=\frac{42}{6}\) = 7
The absolute values of the deviations are |3 – 7|, |6 – 7|, |10 – 7|, |4 – 7|, |9 – 7|, |10 – 7| = 4, 1, 3, 3, 2, 3
∴ The mean deviation about the mean = \(\frac{4+1+3+3+2+3}{6}\)
= \(\frac{16}{6}\)
= 2.66

Question 10.
If the mean and variance of a binomial variable X are 2.4 and 1.44 respectively, find the parameters of the distribution X. (Binomial).
Solution:
X following Binomial distribution with parameters n and p.
mean np = 2.4 ………(1)
variance npq = 1.44 …………(2)
\(\frac{n p q}{n p}=\frac{1.44}{2.4}\)
⇒ q = 0.6
∴ p = 1 – q
= 1 – 0.6
= 0.4
from (1), n(0.4) = 2.4
⇒ n = 6
∴ n = 6, p = 0.4

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Answer ANY FIVE questions.
• Each question carries FOUR marks.

Question 11.
If (x – iy)^1/3 = a – ib, then show that \(\frac{x}{a}+\frac{y}{b}\) = 4(a² – b²).
Solution:
Given (x – iy)^1/3 = a – ib
⇒ x – iy = (a – ib)³
= a³ – 3a²ib + 3ai²b² + i³b³
= a³ – i³a²b – 3ab² + ib³
= (a³ – 3ab²) + i(b³ – 3a²b)
Equating real and imaginary parts on both sides
x = a³ – 3ab², -y = b³ – 3a²b ⇒ y = -(b³ – 3a²b)
\(\frac{x}{a}+\frac{y}{b}=\frac{a^3-3 a b^2}{a}+\frac{-\left(b^3-3 a^2 b\right)}{b}\)
= \(\frac{a^3-3 a b^2}{a}+\frac{3 a^2 b-b^3}{b}\)
= a² – 3b² + 3a² – b²
= 4a² – 4b²
= 4(a² – b²)
∴ \(\frac{x}{a}+\frac{y}{b}\) = 4(a² – b²)

Question 12.
Find the maximum value of the function \(\frac{x^2+14 x+9}{x^2+2 x+3}\) over R.
Solution:
Let y = \(\frac{x^2+14 x+9}{x^2+2 x+3}\)
⇒ yx² + 2xy + 3y = x² + 14x + 9
⇒ (1 – y)x² + (14 – 2y)x + (9 – 3y) = 0
x ∈ R ⇒ (14 – 2y)² – 4(1 – y)(9 – 3y) ≥ 0
⇒ 4(7 – y)² – 4(1 – y)(9 – 3y) ≥ 0
⇒ (7 – y)² – (1 – y)(9 – 3y) ≥ 0
⇒ 49 – 14y + y² – (9 – 3y – 9y + 3y2) ≥ 0
⇒ 49 – 14y + y² – 9 + 12y – 3y² ≥ 0
⇒ -2y² – 2y + 40 ≥ 0
⇒ 2y² + 2y – 40 ≤ 0
⇒ y² + y – 20 ≤ 0
⇒ (y + 5)(y – 4) ≤ 0
⇒ -5 ≤ y ≤ 4
∴ Maximum value = 4, Minimum value = -5

Question 13.
Find the sum of all 4-digit numbers that can be formed using the digits 1, 3, 5, 7, 9.
Solution:
Given digits are 1, 3, 5, 7, 9
The no. of four-digit numbers that can be formed using the digits 1, 3, 5, 7, and 9 is ⁵P₄ = 120
We first find the sum of the digits in the unit place of all these 120 numbers.
If we fill the unit place with 1 then the remaining 3 places can be filled with the remaining 4 digits it can be done in ⁴P₃ ways.
Similarly, each of the digits 3, 5, 7, and 9 appear 24 times in units place.
By adding all these digits, we get
⁴P₃ × 1 + ⁴P₃ × 3 + ⁴P₃ × 5 + ⁴P₃ × 7 + ⁴P₃ × 9
= ⁴P₃ × (1 + 3 + 5 + 7 + 9)
= ⁴P₃ × 25
Similarly, the sum of the digits in ten’s place value as ⁴P₃ × 25 × 10
Similarly, the values of the sum of the digits 100’s place and 1000’s places are ⁴P₃ × 25 × 100 and ⁴P₃ × 25 × 1000
Hence the sum of all the 4 digit numbers formed by using the digits 1, 3, 5, 7, 9 is ⁴P₃ × 25 × 1 + ⁴P₃ × 25 × 10 + ⁴P₃ × 25 × 100 + ⁴P₃ × 25 × 1000
= ⁴P₃ × 25 × (1 + 10 + 100 + 1000)
= ⁴P₃ × 25 × 1111
= 24 × 25 × 1111
= 6,66,600

Question 14.
Prove that: ²⁵C₄ + \(\sum_{r=0}^4{ }^{(29-r)} C_3\) = ³⁰C₄
Solution:

Question 15.
Resolve \(\frac{x^2+5 x+7}{(x-3)^3}\) into partial fractions.
Solution:

Question 16.
A and B are events with P(A) = 0.5, P(B) = 0.4 and P(A ∩ B) = 0.3. Find the probability that:
(i) A does not occur
(ii) Neither A nor B occurs
Solution:
Given P(A) = 0.5, P(B) = 0.4 and P(A ∩ B) = 0.3
(i) The probability that A does not occur = P(\(\bar{A}\))
= 1 – P(A)
= 1 – 0.5
= 0.5
(ii) The probability that neither A nor B occurs = P(\(\overline{\mathrm{A}} \cap \overline{\mathrm{B}}\))
= P(\(\overline{A \cup B}\))
= 1 – P(A ∪ B)
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 – [0.5 + 0.4 – 0.3]
= 1 – 0.6
= 0.4

Question 17.
A problem in calculus is given to two students A and B whose chances of solving it are \(\frac{1}{3}\) and \(\frac{1}{4}\) respectively. Find the probability of the problem being solved if both of them try independently.
Solution:
Let E₁ and E₂ denote the events that the problem is solved by A and B respectively.
Given P(E₁) = \(\frac{1}{3}\) and P(E₂) = \(\frac{1}{4}\)
By addition theorem on probability, we have
P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
Since E₁, E₂ are independent = P(E₁) + P(E₂) – P(E₁) . P(E₂)
= \(\frac{1}{3}+\frac{1}{4}-\frac{1}{3} \cdot \frac{1}{4}\)
= \(\frac{4+3-1}{12}\)
= \(\frac{6}{12}\)
= \(\frac{1}{2}\)

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Answer ANY FIVE questions.
• Each question carries SEVEN marks.

Question 18.
If n is a positive integer, show that \((P+i Q)^{\frac{1}{n}}+(P-i Q)^{\frac{1}{n}}=2\left(P^2+Q^2\right)^{\frac{1}{2 n}} \cdot \cos \left[\frac{1}{n} \tan ^{-1} \frac{Q}{P}\right]\)
Solution:

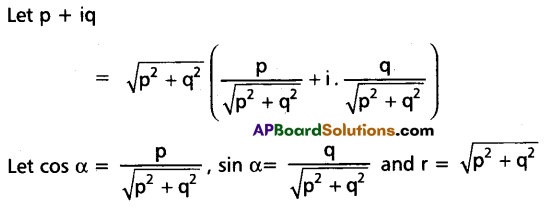
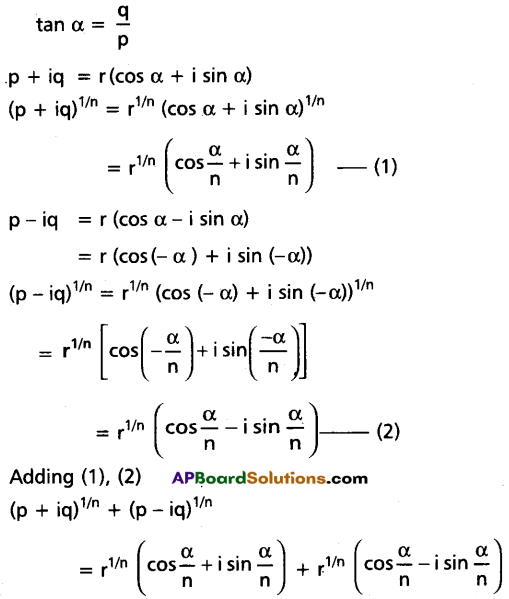
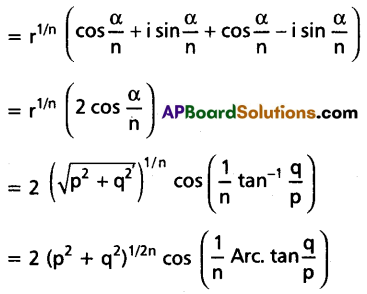
Question 19.
Solve the equation 6x⁶ – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0.
Solution:
Given 6×6 – 25x⁵ + 31x⁴ – 31x² + 25x – 6 = 0
∴ Given equation is an even degree reciprocal equation of class two.
∴ 1 and -1 are the roots of the given equation.
∴ (x – 1) and (x + 1) are the factors of the given equation.

(x – 1) (x + 1) (6x⁴ – 25x³ + 37x² – 25x + 6) = 0
Take 6x⁴ – 25x³ + 37x² – 25x + 6 = 0
⇒ 6x² – 25x + 37x – 25 . \(\frac{1}{x}\) + 6 . \(\frac{1}{x^2}\) = 0
⇒ \(6\left(x^2+\frac{1}{x^2}\right)-25\left(x+\frac{1}{x}\right)\) + 37 = 0
Let x + \(\frac{1}{x}\) = t
Then x² + \(\frac{1}{x^2}\) = \(\left(x+\frac{1}{x}\right)^2\) – 2 = t² – 2
∴ 6(t² – 2) – 25t + 37 = 0
⇒ 6t² – 12 – 25t + 37 = 0
⇒ 6t² – 25t + 25 = 0
⇒ 6t² – 10t – 15t + 25 = 0
⇒ 2t(3t – 5) – 5(3t – 5) = 0
⇒ (3t – 5) (2t – 5) = 0
⇒ 3t – 5 = 0 (or) 2t – 5 = 0
∴ 3t – 5 = 0
3(x + \(\frac{1}{x}\)) – 5 = 0
⇒ 3x² + 3 – 5x = 0
⇒ 3x² – 5x + 3 = 0
⇒ x = \(\frac{5 \pm \sqrt{25-4.3 .3}}{2-3}\)
⇒ x = \(\frac{5 \pm i \sqrt{11}}{6}\)
∴ 2t – 5 = 0
⇒ 2(x + \(\frac{1}{x}\)) – 5 = 0
⇒ 2x² + 2 – 5x = 0
⇒ 2x² – 5x + 2 = 0
⇒ 2x² – 4x – x + 2 = 0
⇒ 2x(x – 2) – 1(x – 2) = 0
⇒ (x – 2) (2x – 1) = 0
⇒ x = 2, \(\frac{1}{2}\)
Hence the roots of the given equation are 1, -1, 2, \(\frac{1}{2}\), \(\frac{5 \pm i \sqrt{11}}{6}\)

Question 20.
For r = 0, 1, 2, ……n, prove that: C₀C_r + C₁C_r+1 + C₂C_r+2 + ……… + C_n = ²ⁿC_(n+r) and hence deduce that:
(i) \(C_0^2+C_1^2+C_2^2+\ldots \ldots \ldots \ldots \ldots+C_n^2={ }^{2 n} C_n\)
(ii) C₀C₁ + C₁C₂ + C₂C₃ + …….. + C_n-1 . C_n = ²ⁿC_n+1.
Solution:

Question 21.
Find the sum to infinite terms of the series: \(\frac{7}{.5}\left(1+\frac{1}{10^2}+\frac{1.3}{1.2} \cdot \frac{1}{10^4}+\frac{1.3 .5}{1.2 .3} \cdot \frac{1}{10^6}+\ldots . . \infty\right)\)
Solution:

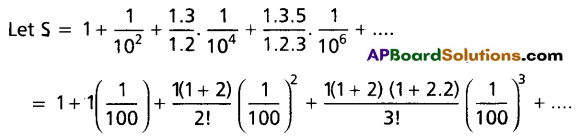
Question 22.
Find the mean deviation from the mean of the following data, using the step deviation method:

Marks	No. of Students
0-10	6
10-20	5
20-30	8
30-40	15
40-50	7
50-60	6
60-70	3

Solution:
Let assumed mean A = 35 then d_i = \(\frac{x_i-35}{10}\)

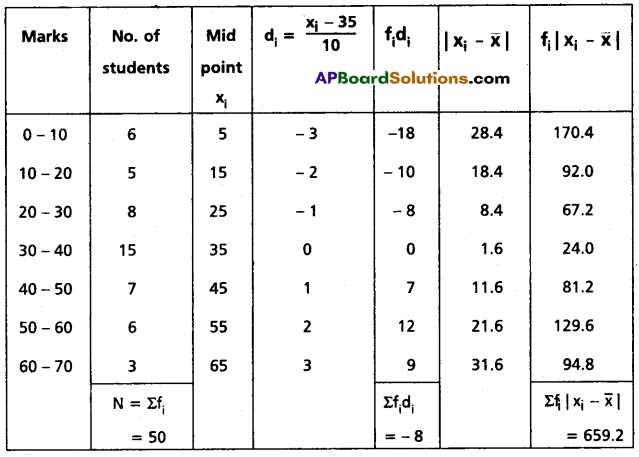
Mean \(\overline{\mathbf{x}}=\mathrm{A}+\left(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\mathrm{N}}\right)_h\)
= 35 + (\(\frac{-8}{50}\)) 10
= 35 – 1.6
= 33.4
Mean deviation from Mean = \(\frac{1}{N} \Sigma f_i\left|x_i-\bar{x}\right|\)
= \(\frac{1}{50}\) (659.2)
= 13.18

Question 23.
(a) State and prove the Addition theorem on probability.
(b) Find the probability of drawing an ace or a spade from a well-shuffled pack of 52 playing cards.
Solution:
(a) Statement: If E₁ and E₂ are any two events of a random experiment and P is the probability function.
Then P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
Case (i): When E₁ ∩ E₂ = φ
⇒ P(E₁ ∩ E₂) = 0
∴ P(E₁ ∪ E₂) = P(E₁) + P(E₂) [∵ from the union axiom]
= P (E₁) + P(E₂) – 0
= P(E₁) + P(E₂) – P(E₁ ∩ E₂)
Case (ii): When E₁ ∩ E₂ = φ
E₁ ∪ E₂ can be expressed as union of 2 mutually exclusive events E₁ – E₂, E₂.
Hence, E₁ ∪ E₂ = (E₁ – E₂) ∪ E₂ also (E₁ – E₂) ∩ E₂ = φ
∴ P(E₁ ∪ E₂) = P[(E₁ – E₂) ∪ E₂]
= P(E₁ – E₂) + P(E₂) ……..(1) [∵ From the union axiom]
Also, E₁ can be expressed as the union of 2 mutually exclusive events E₁ – E₂, E₁ ∩ E₂.
Hence, E₁ = (E₁ – E₂) ∪ (E₁ ∩ E₂), also (E₁ – E₂) ∩ (E₁ ∩ E₂) = φ
∴ P(E₁) = P(E₁ – E₂) ∪ (E₁ ∩ E₂)] = P(E₁ – E₂) + P (E₁ ∩ E₂)
⇒ P(E₁ – E₂) = P(E₁) – P(E₁ ∩ E₂)
From (1),
∴ P(E₁ ∪ E₂) = P(E₁) – P(E₁ ∩ E₂) + P(E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)

(b) Let A be the event that gets an ace and B be the event that gets a spade card from a well-shuffled pack of 52 playing cards S is the sample space.

Question 24.
If X is a random variable with probability distribution P(X = k) = \(\frac{(k+1) C}{2^k}\), k = 0, 1, 2, 3,………. then find C.
Solution:
Given X is a random variable with a probability distribution
P(X = k) = \(\frac{(k+1) C}{2^k}\), k = 0, 1, 2, 3,……