Thoroughly analyzing AP Inter 2nd Year Maths 2A Model Papers and AP Inter 2nd Year Maths 2A Question Paper March 2017 helps students identify their strengths and weaknesses.
AP Inter 2nd Year Maths 2A Question Paper March 2017
Time: 3 Hours
Maximum Marks: 75
Note: This question paper consists of THREE Sections A, B, and C.
Section – A
(10 × 2 = 20 Marks)
I. Very Short Answer Type Questions:
- Answer ALL questions.
- Each question carries TWO marks.
Question 1.
Write the complex, number (2 – 3i) (3 + 4i) in the form A + iB.
Solution:
(2 – 3i) (3 + 4i) = 6 + 8i – 9i – 12i2
= 6 – i – 12(-1)
= 6 – i + 12
= 18 – i
= 18 + i(-1)
= A + iB where A = 18, B = -1
Question 2.
If z1 = -1 and z2 = i, then find Arg(\(\frac{z_1}{z_2}\)).
Solution:
z1 = -1 cos π + i sin π
∴ Arg (z1) = π
z2 = i = cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\)
∴ Arg z2 = \(\frac{\pi}{2}\)
Arg(\(\frac{z_1}{z_2}\)) = Arg z1 – Arg z2
= π – \(\frac{\pi}{2}\)
= \(\frac{\pi}{2}\)
∴ \({Arg}\left(\frac{z_1}{z_2}\right)=\frac{\pi}{2}\)
![]()
Question 3.
If 1, ω, ω6 are the cube roots of unity, prove that: (a + b) (aω + bω2) (aω2 + bω) = a3 + b3.
Solution:
(a + b) (aω + bω2) (aω2 + bω)
= (a + b) [a2 ω3 + abω2 + abω2 + b2ω3]
= (a + b) [a2 + ab(ω2 + ω4) + b2]
= (a + b) [a2 + ab(ω2 + ω) + b2]
= (a + b) (a2 – ab + b2)
= a3 + b3
Question 4.
Find the values of m for which the equation x2 – 15 – m(2x – 8) = 0 have equal roots.
Solution:
Given equation is x2 – 15 – m(2x – 8) = 0
⇒ x2 – 2mx + 8m – 15 = 0
If the equation ax2 + bx + c = 0 has equal roots then its discriminant is zero.
∵ The roots are equal ⇒ b2 – 4ac = 0
a = 1, b = -2m, c = 8m – 15
b2 – 4ac = (-2m)2 – 4(1) (8m – 15)
= 4m2 – 32m + 60
= 4(m2 – 8m + 15)
= 4(m – 3) (m – 5)
∴ b2 – 4ac = 0
⇒ 4(m – 3) (m – 5) = 0
⇒ m – 3 = 0 or m – 5 = 0
⇒ m = 3 or 5
Question 5.
If the product of the roots of 4x3 + 16x2 – 9x – a = 0 is 9, then find a.
Solution:
α, β, γ are the roots of 4x3 + 16x2 – 9x – a = 0
αβγ = 9
⇒ \(\frac{a}{4}\) = 9
⇒ a = 36
Question 6.
Find the number of different chains that can be prepared using 7 different coloured beads.
Solution:
We know that the number of circular permutations of hanging type that can be formed using n things is \(\frac{1}{2}\) {(n – 1)!}.
Hence the number of chains is \(\frac{1}{2}\) {(7 – 1)!} = \(\frac{1}{2}\) (6!) = 360.
Question 7.
If nPr = 5040 and nCr = 210, find n and r.
Solution:
Hint: nPr = r! nCr and nPr = n(n – 1) (n – 2), …… [n – (r – 1)]
nPr = 5040, nCr = 210
r! = \(\frac{{ }^n P_r}{{ }^n C_r}=\frac{5040}{210}=\frac{504}{21}\) = 24 = 4!
∴ r = 4
nPr = 5040
⇒ nP4 = 5040
⇒ nP4 = 10 × 504
⇒ nP4 = 10 × 9 × 56
⇒ nP4 = 10 × 9 × 8 × 7
⇒ nP4 = 10P4
∴ n = 10
∴ n = 10, r = 4
![]()
Question 8.
Find the set E of the values of x for which the binomial expansion of \((3-4 x)^{\frac{3}{4}}\) is valid.
Solution:
\((3-4 x)^{3 / 4}=3^{3 / 4}\left(1-\frac{4 x}{3}\right)^{3 / 4}\)
The binomial expansion of \((3-4 x)^{\frac{3}{4}}\) is valid, when \(\left|\frac{4 x}{3}\right|\) < 1
i.e., |x| < \(\frac{3}{4}\)
i.e., E = \(\left(\frac{-3}{4}, \frac{3}{4}\right)\)
Question 9.
Find the mean deviation about the median for the following data:
4, 6, 9, 3, 10, 13, 2.
Solution:
Given ungrouped data are 4, 6, 9, 3, 10, 13, 2
Expressing the data in ascending order of magnitude,
we have 2, 3, 4, 6, 9, 10, 13
∴ Median = 6 = b (say)
The absolute values are |6 – 2|, |6 – 3|, |6 – 4|, |6 – 6|, |6 – 9|, |6 – 10|, |6 – 13| = 4, 3, 2, 0, 3, 4, 7
∴ Mean deviation from the median = \(\frac{\sum_{i=1}^7\left|x_i-b\right|}{7}\)
= \(\frac{4+3+2+0+3+4+7}{7}\)
= \(\frac{23}{7}\)
= 3.285
Question 10.
The probability that a person chosen at random is left-handed (in handwriting) is 0.1. What is the probability that in a group of 10 people, there is one who is left-handed?
Solution:
Here n = 10, p = 0.1
q = 1 – p = 1 – 0.1 = 0.9
P(X = 1) = 10C1 (0.1)1 (0.9)10-1
= 10 × 0.1 × (0.9)9
= 1 × (0.9)9
= (0.9)9
Section – B
(5 × 4 = 20 Marks)
II. Short Answer Type Questions:
- Answer ANY FIVE questions.
- Each question carries FOUR marks.
Question 11.
If the point P denotes the complex number z = x + iy in the Argand plane and if \(\frac{z-i}{z-1}\) is a purely imaginary number, find the locus of P.
Solution:
We note that the quotient \(\frac{z-i}{z-1}\) is not defined if z = 1.
Since z = x + iy
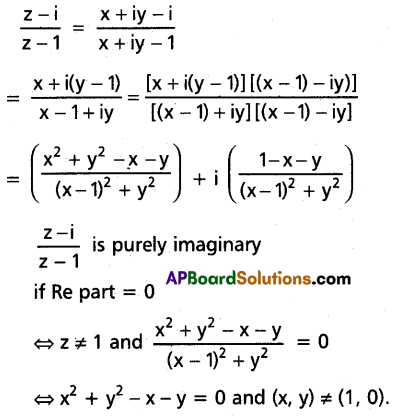
∴ The locus of P is the circle x2 + y2 – x – y = 0 excluding the point (1, 0).
Question 12.
Prove that \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4, if x is real.
Solution:
Let y = \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\)
y = \(\frac{x+1+3 x+1-1}{(3 x+1)(x+1)}\)
y = \(\frac{4 x+1}{3 x^2+3 x+x+1}\)
y = \(\frac{4 x+1}{3 x^2+4 x+1}\)
⇒ 3yx2 + 4yx + 4 = 4x + 1
⇒ 3yx2 + (4y – 4)x + (y – 1) = 0
x ∈ R ⇒ (4y – 4)2 – 4(3y) (y – 1) ≥ 0
⇒ 16y2 – 32y + 16 – 12y2 + 12y ≥ 0
⇒ 4y2 – 20y + 16 ≥ 0
⇒ 4y2 – 20y + 16 = 0
⇒ y2 – 5y + 4 = 0
⇒ (y – 1) (y – 4) = 0
⇒ y = 1, 4
⇒ 4y2 – 20y + 16 ≥ 0
⇒ y ≤ 1 (or) y ≥ 4
⇒ y does not lie between 1 and 4.
Since the y2 coefficient the exp ≥ 0.
∴ \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4.
![]()
Question 13.
If the letters of the word PRISON are permuted in all possible ways and the words thus formed are arranged in dictionary order, find the rank of the word PRISON.
Solution:
The letters of the given word in dictionary order are I N O P R S
In the dictionary order, first, all the words that begin with I come.
If I occupy the first place then the remaining 5 places can be filled with the remaining 5 letters in 5! ways.
Thus, there are 5! number of words that begin with I.
On proceeding like this we get
I → 5! ways
N → 5! ways
O → 5! ways
P I → 4! ways
P N → 4! ways
P O → 4! ways
P R I N → 2! ways
P R I O → 2! ways
P R I S N O → 1 way
P R I S O N → 1 way
Hence the rank of PRISON is 3 × 5! + 3 × 4! + 2 × 2! + 1 × 1 = 360 + 72 + 4 + 1 + 1 = 438.
Question 14.
Simplify \({ }^{34} C_5+\sum_{r=0}^4{ }^{(38-r)} C_4\).
Solution:

Question 15.
Resolve \(\frac{x^2-3}{(x+2)\left(x^2+1\right)}\) into partial fractions.
Solution:
Let \(\frac{x^2-3}{(x+2)\left(\dot{x}^2+1\right)}=\frac{A}{x+2}+\frac{B x+C}{x^2+1}\)
⇒ \(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{A\left(x^2+1\right)+(B x+C)(x+2)}{(x+2)\left(x^2+9\right)}\)
⇒ x2 – 3 = A(x2 + 1) + (Bx + C) (x + 2) ………(1)
Put x = -2 in (1)
(-2)2 – 3 = A[(-2)2 + 1]
⇒ 4 – 3 = A(4 + 1)
⇒ 1 = 5A
⇒ A = \(\frac{1}{5}\)
In (1), Comparing the coefficients of x2 on both sides, we have
1 = A + B
⇒ B = 1 – A
⇒ B = 1 – \(\frac{1}{5}\)
⇒ B = \(\frac{4}{5}\)
In (1), Comparing constant terms on both sides, we have
-3 = A + 2C
⇒ 2C = -3 – A
⇒ 2C = -3 – \(\frac{1}{5}\)
⇒ 2C = \(\frac{-16}{5}\)
⇒ C = \(\frac{-8}{5}\)
∴ A = \(\frac{1}{5}\), B = \(\frac{4}{5}\), C = \(\frac{-8}{5}\)
∴ \(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{\frac{1}{5}}{x+2}+\frac{\frac{4}{5} x-\frac{8}{5}}{x^2+1}\) = \(\frac{1}{5(x+2)}+\frac{4 x-8}{5\left(x^2+1\right)}\)
Question 16.
State and prove the Addition theorem on probability.
Solution:
Statement: If E1 and E2 are any two events of a random experiment and P is a probability function, then P(E1 ∪ E2) = P(E1) + P(E2) – P(E1 ∩ E2).
Proof: Case (i): E1 ∩ E2 = φ
Then P(E1 ∩ E2) = 0
∴ P(E1 ∪ E2) = P(E1) + P(E2)
= P(E1) + P(E2) – 0
= P(E1) + P(E2) – P(E1 ∩ E2)
Case (ii): Suppose E1 ∩ E2 ≠ φ
Then E1 ∪ E2 = E1 ∪ (E2 – E1) and E1 ∩ (E2 – E1) = φ
∴ P(E1 ∪ E2) = P[E1 ∪ (E2 – E1)]
= P(E1) + P(E2 – E1)
= P(E1) + P[E2 – (E1 ∩ E2)
Since E2 ∩ (E1 ∩ E2) = φ = P(E1) + P(E2) – P(E1 ∩ E2)
Hence P(E1 ∪ E2) = P(E1) + P(E2) – P(E1 ∩ E2)
![]()
Question 17.
Suppose A and B are independent events with P(A) = 0.6, and P(B) = 0.7. Then compute:
(i) P(A ∩ B)
(ii) P(A ∪ B)
(iii) P(\(\frac{B}{A}\))
(iv) P(Ac ∩ Bc)
Solution:
Given A, B are independent events and P(A) = 0.6, P(B) = 0.7
(i) P(A ∩ B) = P(A) P(B) = 0.6 × 0.7 = 0.42
(ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.6 + 0.7 – 0.42
= 1.3 – 0.42
= 0.88
(iii) P(B/A) = P(B) = 0.7
(iv) P(AC ∩ BC) = P(AC) . P(BC) (∵ AC & BC are also independent events)
= [1 – P(A)] [1 – P(B)]
= (1 – 0.6) (1 – 0.7)
= 0.4 × 0.3
= 0.12
Section – C
(5 × 7 = 35 Marks)
III. Long Answer Type Questions.
- Answer ANY FIVE questions.
- Each question carries SEVEN marks.
Question 18.
If n is an integer then show that: (1 + cos θ + i sin θ)n + (1 + cos θ – i sin θ)n = 2n+1 cos(\(\frac{\theta}{2}\)) cos(\(\frac{n \theta}{2}\)).
Solution:

Question 19.
Solve the equation: 2x5 + x4 – 12x3 – 12x2 + x + 2 = 0.
Solution:
Given f(x) = 2x5 + x4 – 12x3 – 12x2 + x + 2 = 0
This is an odd-degree reciprocal equation of the first type.
∴ -1 is a root.

Dividing f(x) by (x + 1), we get 2x4 – x3 – 11x2 – 11x + 2 = 0
Dividing by x2,
2x2 – x – 11 – \(\frac{1}{x}+\frac{2}{x^2}\) = 0
\(2\left(x^2+\frac{1}{x^2}\right)-\left(x+\frac{1}{x}\right)-11=0\) …….(1)
Put a = x + \(\frac{1}{x}\) so that x2 + \(\frac{1}{x^2}\) = a2 – 2
Substituting in (1), the required equation is
2(a2 – 2) – a – 11 = 0
⇒ 2a2 – 4 – a – 11 = 0
⇒ 2a2 – a – 15 = 0
⇒ (a – 3) (2a + 5) = 0
⇒ a = 3 (or) a = \(\frac{-5}{2}\)
Case (1): a = 3
x + \(\frac{1}{x}\) = 3
⇒ x2 + 1 = 3x
⇒ x2 – 3x + 1 = 0
⇒ x = \(\frac{3 \pm \sqrt{9-4.1 .1}}{2}\)
⇒ x = \(\frac{3 \pm \sqrt{9-4}}{2}\)
⇒ x = \(\frac{3 \pm \sqrt{5}}{2}\)
Case (2): a = \(\frac{-5}{2}\)
x + \(\frac{1}{x}\) = \(\frac{-5}{2}\)
⇒ \(\frac{x^2+1}{x}=\frac{-5}{2}\)
⇒ 2x2 + 2 = -5x
⇒ 2x2 + 5x + 2 = 0
⇒ (2x + 1) (x + 2) = 0
⇒ x = \(\frac{-1}{2}\), -2
∴ The roots of the given equation are -1, \(\frac{3 \pm \sqrt{5}}{2}\), -2, \(\frac{-1}{2}\).
![]()
Question 20.
If the coefficients of 4 consecutive terms in the expansion of (1 + x)n are a1, a2, a3, a4 respectively, then show that: \(\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{2 a_2}{a_2+a_3}\)
Solution:
Given a1, a2, a3, a4 are the coefficients of 4 consecutive terms in (1 + x)n respectively.


Question 21.
If x = \(\frac{1.3}{3.6}+\frac{1 \cdot 3.5}{3 \cdot 6.9}+\frac{1 \cdot 3 \cdot 5 \cdot 7}{3 \cdot 6 \cdot 9 \cdot 12}\) + …….., then Prove that 9x2 + 24x = 11.
Solution:
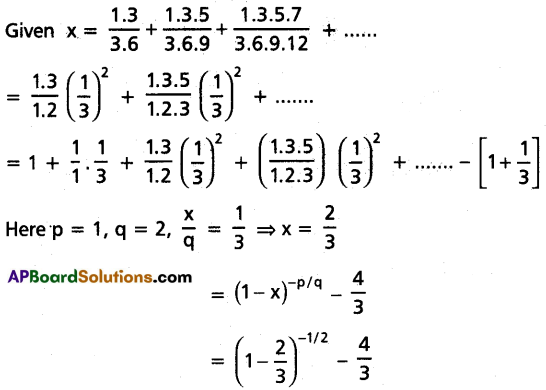
= \(\left(\frac{1}{3}\right)^{-1 / 2}-\frac{4}{3}\)
= \(\sqrt{3}-\frac{4}{3}\)
⇒ 3x + 4 = 3√3
Squaring on both sides
(3x + 4)2 = (3√3)2
⇒ 9x2 + 24x + 16 = 27
⇒ 9x2 + 24x = 11
Question 22.
Find the mean deviation about the mean for the following data:
| Marks Obtained | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| No. of Students | 5 | 8 | 15 | 16 | 6 |
Solution:
Taking the assumed mean a = 25 and h = 10
Construct the table

∴ Mean deviation from the mean = \(\frac{1}{N} \Sigma f_i\left|x_i-\bar{x}\right|\)
= \(\frac{1}{50}\)(477)
= 9.54
Question 23.
Three urns have the following composition of balls:
Urn I: 1 white, 2 black
Urn II: 2 white, 1 black
Urn III: 2 white, 2 black
One of the urns is selected at random and a ball is drawn. It turns out to be white. Find the probability that it came from urn III.
Solution:
Let Ei be the event of choosing the Urn i = 1, 2, 3 and P(Ei) be the probability of choosing the Urn i = 1, 2, 3.
Then P(E1) = P(E2) = P(E3) = \(\frac{1}{3}\)
Having choosen the Urn i, the probability of drawing a white ball, P(W/Ei), is given by
P(W/E1) = \(\frac{1}{3}\); P(W/E2) = \(\frac{2}{3}\); P(W/E3) = \(\frac{2}{4}\)
We have to find the probability P(E3/W) by Baye’s theorem.
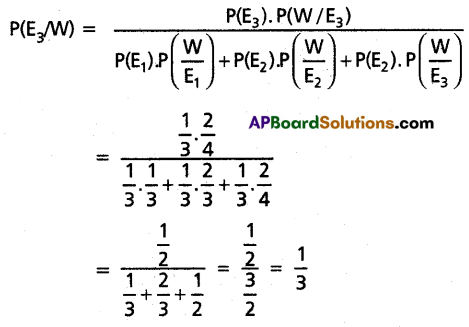
![]()
Question 24.
The probability distribution of a random variable X is given below:
| X = xi | P(X = xi) |
| 1 | k |
| 2 | 2k |
| 3 | 3k |
| 4 | 4k |
| 5 | 5k |
Find the value of k and the mean and variance of X.
Solution:
We have \(\sum_{i=1}^5 P\left(X=x_i\right)\) = 1
⇒ k + 2k + 3k + 4k + 5k = 1
⇒ k = \(\frac{1}{15}\)
Mean μ of x = \(\sum_{r=1}^5 r \cdot p\left(X=x_i\right)=\sum_{r=1}^5 r(r k)\)
= 1.(k) + 2.(2k) + 3.(3k) + 4.(4k) + 5.(5k)
= 55k
= 55 × \(\frac{1}{15}\)
= \(\frac{11}{3}\)
variance (σ2) = (1)2 . k + (2)2 . 2k + (3)2 . 3k + (4)2 . 4k + (5)2 (5k) – µ2
= k + 8k + 27k + 64k + 125k – \(\left(\frac{11}{3}\right)^2\)
= 225k – \(\frac{121}{9}\)
= 225 × \(\frac{1}{15}\) – \(\frac{121}{9}\)
= \(\frac{135-121}{9}\)
= \(\frac{14}{9}\)