AP Inter 1st Year Physics Question Paper May 2017

Thoroughly analyzing AP Inter 1st Year Physics Model Papers and AP Inter 1st Year Physics Question Paper May 2017 helps students identify their strengths and weaknesses.

AP Inter 1st Year Physics Question Paper May 2017

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer ALL questions.
• Each question carries TWO marks.
• ALL are very short Answer type questions.

Question 1.
What is the discovery of C.V. Raman ?
Answer:
In elastic scattering of light by molecules.

Question 2.
How can systematic errors be minimised or eliminated ?
Answer:
Systematic errors can be minimised by improving experimental techniques, selecting better instruments and removing personal bias as far as possible. For a given set up, these errors may be estimated to a certain extent and the necessary corrections may be applied to the readings.

Question 3.
How is average velocity different from instantaneous velocity ?
Answer:
The average velocity does not give any details of the motion of the particle. It gives only the result of the motion. The instantaneous velocity defines how fast the particle moves at a particular instant of time.

Question 4.
Give an example where the velocity of an object is zero but its acceleration is not zero.
Answer:
When the body is projected vertically upwards, at highest point, its velocity is zero. But its acceleration (a = g) is not equal to zero.

Question 5.
Two forces of magnitudes 3 units and 5 units act at 60° with each other. What is the magnitude of their resultant ?
Answer:
θ = 60°, P = 3 units, Q = 5 units,
Resultant (R) = \(\sqrt{P^2+Q^2+2 P Q \cos \theta}\)
R = \(\sqrt{3^2+5^2+2 \times 3 \times 5 \cos 60^{\circ}}\) = \(\sqrt{9+25+30 \times \frac{1}{2}}\)
= \(\sqrt{49}\) = 7 units.

Question 6.
According to Newton’s third law, every force is accompanied by an equal and opposite force. How can a movement ever take place.
Answer:
Action and reaction always takes place on two different bodies, they never cancel each other. So motion is possible.

Question 7.
What is magnus effect ?
Answer:
The difference in the velocities of air results in the pressure difference between the lower and upper faces and there is a net upward force on the ball. This dynamic lift due to spinning is called magnus effect.

Question 8.
Why are drops and bubbles spherical ?
Answer:
The surface tension of a liquid tends to have minimum surface area. For a given volume, the surface area is minimum for a sphere. Hence rain drops are spherical shape.

Question 9.
What is latent heat of fusion ?
Answer:
The amount of heat required to convert unit mass of ice at 0°C into water at 0°C, is called latent heat of fusion.

Question 10.
State Newton’s law of cooling.
Answer:
“The rate of loss of heat of the body is directly proportional to the difference of temparature of the body ar d the surroundings”

Section – B (6 × 4 = 24)

Note :

• Answer any SIX questions.
• Each question carries FOUR marks.
• ALL are short answer type Questions.

Question 11.
Show that the trajectory of an object thrown at certain angle with the horizontal is a parabola.
Answer:
Consider a body is projected with an initial velocity (u) making an angle θ with the horizontal. The body does not experience acceleration in horizontal direction. The velocity of the projectile can be resolved into (i) u cos θ, horizontal component (ii) u sin θ, vertical component. The horizontal component of velocity remains constant through out the motion. Only its vertical component changes due to acceleration due to gravity (g).

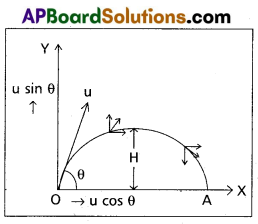
The distance travelled along OX in time t is given by
x = u cos θ × t
t = \(\frac{\mathrm{x}}{\mathrm{u} \cos \theta}\) → (1)
The distance travelled along by in time t is given by
y = (u cos θ) t \(\frac{1}{2}\) gt² → (2)
Substituting eq. (1) in eq. (2)
y = (u sin θ) \(\frac{\mathrm{x}}{\mathrm{u} \cos \theta}\) – \(\frac{1}{2}\) g (\(\frac{x^2}{u^2 \cos ^2 \theta}\)) [∵ u = u sin θ, a = -g, s = y]
y = x tan θ – (\(\frac{g}{2 u^2 \cos ^2 \theta}\)) x²
Let A = tan θ and B = \(\frac{g}{2 u^2 \cos ^2 \theta}\)
Y = Ax – Bx² Where A and B are constants.
This is the equation of parabola.
∴ The trajectory of a projectile is parabola.

Question 12.
State Newton’s second law of motion. Hence derive the equation of motion F = ma from it.
Answer:
Newton’s second law motion : The rate of change of momentum of a body is directly proportional to the external force applied and takes place in the same direction”.

To Show F = ma : Let a body of mass’m’ moving with velocity ‘V’ under the action of an external force F in the direction of velocity.

Momentum ‘P’ of a body is the product of the mass and velocity v.
∴ P = mv → (1)
According to Newton’s Second Law of motion, we have
\(\frac{\mathrm{dp}}{\mathrm{dt}}\) ∝ F, F = external force
(or) F = K\(\frac{\mathrm{dp}}{\mathrm{dt}}\) → (2)
From equations (1) and (2) we have
F = K \(\frac{\mathrm{d}(\mathrm{mv})}{\mathrm{dt}}\) = K.m \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = Kma → (3)
Since the rate of change of velocity \(\frac{\mathrm{dv}}{\mathrm{dt}}\) is the acceleration ‘a’ of the body.
In SI system the unit of force is Newton and is defined as that force which when acting on a body of mass 1 kg produces in it an acceleration of 1 ms^-2.
i. e., from equation (3),
If F = 1, m = 1 and a = 1 we get K = 1
Hence F = \(\frac{\mathrm{dp}}{\mathrm{dt}}\) = ma
∴ F = ma

Question 13.
Distinguish between centre of mass and centre of gravity.
Answer:

Centre of mass	Centre of gravity
1. Point at which entire mass of the body is supposed to be concentrated, and the motion of the point represents motion of the body.	1. Fixed point through which the weight of the body act.
2. It refers mass of to body.	2. It refers to the weight acting on all particles of the body
3. In a uniform gravitational field centre of mass and centre of gravity coincide	3. In a non-uniform gravitational field, centre of gravity and centre of mass do not coincide.
4. Centre of mass of the body is defined to describe the nature of motion of a body as a whole.	4. Centre of gravity of body is defined to know the amount of stability of the body when supported.

Question 14.
Define vector product. Explain the properties of a vector product with two examples.
Answer:
The cross product of two vectors is given by \(\vec{C}\) = \(\vec{A}\) × \(\vec{B}\) . The magnitude of the vector defined from cross product of two vectors is equal to product of magnitudes of the vectors and sine of angle between the vectors.

Direction of the vectors is given by right hand corkscrew rule and is perpendicular to the plane containing the vectors.
∴ | \(\vec{C}\) | = AB sin θ. and \(\vec{C}\) = AB sin θ n̂.
When, n̂ is the unit vector perpendicular to the plane containing the vectors \(\vec{A}\) and \(\vec{B}\)

Example :
1) Torque is cross product of position vector and Force.
i.e., \(\vec{T}\) = \(\vec{r}\) × \(\vec{F}\)

2) Angular momentum is cross product of position vector and momentum
i.e., \(\vec{L}\) = \(\vec{r}\) × \(\vec{P}\)

Properties :
1) Cross product does not obey commutative law. But its magnitude obey’s commutative law.
\(\vec{A}\) × \(\vec{B}\) ≠ \(\vec{B}\) × \(\vec{A}\) = (\(\vec{A}\) × \(\vec{B}\)) = – (\(\vec{B}\) × \(\vec{A}\)) , |(\(\vec{A}\) × \(\vec{B}\))| = |(\(\vec{B}\) × \(\vec{A}\))|

2) It obeys distributive law \(\vec{A}\) × (\(\vec{B}\) × \(\vec{C}\)) = \(\vec{A}\) × \(\vec{B}\) + \(\vec{A}\) × \(\vec{C}\)

3) The magnitude of cross product of two vectors which are parallel is zero.
Since θ = 0; | \(\vec{A}\) × \(\vec{B}\) | = AB sin 0° = 0

4) For perpendicular vectors, θ = 90°, | \(\vec{A}\) × \(\vec{B}\) | = AB sin 90° | n̂ | = AB

Question 15.
What is escape velocity ? Obtain an expression for it.
Answer:
Escape velocity : It is the minimum velocity with which a body should be projected, so that it moves into the space by overcoming the earth’s gravitational field.

Expression for escape velocity :
Consider a body of mass m thrown with a velocity V_e.
Then K.E = 1\(\frac{1}{2}\) mv_e² ……….. (1)
The gravitational force of attraction of the earth of mass M and Radius R on a body of mass m at its surface is
F = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) …………. (2)
Gravitational P.E. = work done on the body
∴ P.E. = F × R = \(\frac{\mathrm{GMm}}{\mathrm{R}^2}\) x R, P.E. = \(\frac{\mathrm{GMm}}{\mathrm{R}}\) …………. (3)
A body just escapes when its K.E. = P.E.

∴ Escape velocity is √2 times the orbital velocity.

Question 16.
Explain the concept of elastic potential energy in a stretched wire and hence obtain the expression for it.
Answer:
The potential energy stored in a body when stretched is called strain energy.

Let us consider a wire of length L and cross-sectional area A. Let x be the change in length of the wire by the application of stretching force F.
Young’s modulus = \(\frac{\text { Longitudinal Stress }}{\text { Longitudinal Strain }}\)
y = \(\frac{\mathrm{FL}}{\mathrm{Ax}}\)
F= \(\frac{\mathrm{yAx}}{\mathrm{L}}\) ………. (1)
To stretch the wire further by dx, the workdone
dw = F.dx
dw = (\(\frac{\mathrm{yAx}}{\mathrm{L}}\)) dx
Total workdone to stretch the wire from O to x is given by

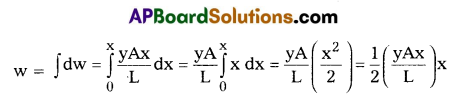
w = \(\frac{1}{2}\)F.x = \(\frac{1}{2}\) × stretching force × elongation
The work done is stored in the form of potential energy.
u = \(\frac{1}{2}\)F.x ……….. (2)
Strain energy per unit volume = \(\frac{1}{2}\) × \(\frac{F x}{A L}\)
= \(\frac{1}{2}\) × Stress × Strain

Question 17.
In what way’is the anomalous behaviour of water advantageous to aquatic animals ?
Answer:
In cold countries, as atmospheric temperature decreases, the upper layer of the lakes, rivers etc., cool, contract and sink to the bottom (fig). This goes on until the whole of the water reaches the temperature of 4°C. When the top layers cool further temperature falls below 4°C, it expands and becomes lighter. It does not sink downwards and remains at the top. With further cooling the top layer gradually form ice at the top (fig). Ice and water are bad conductors of heat. So the lower layers are protected against freezing by the layers of ice and cold water at 1°C, 2°C and 3°C. This results in water remaining at the bottom at 4°C. So that aquatic animals survive in those layers of water.

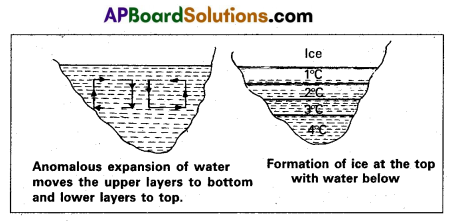
Question 18.
How specific heat capacity of monoatomic, diatomic gases can be explained on the basis of law of equipartition of energy ?
Answer:
Specific heat capacity :
1) Monoatomic gases : According to law of equipartition of energy, a molecule of monoatomic gas has only 3 (translational) degrees of freedom, i.e., f = 3.
The molar specific heat of the gas constant volume is given by c_µ = \(\frac{f}{2}\) R where f is degree of freedom.
∴ C_v = \(\frac{3}{2}\) R = 3 cal/mole k [∴ R = 2 cal/mole – k]
The molar specific heat at constant pressure is given by
C_p = (\(\frac{f}{2}\) + 1) R = (\(\frac{3}{2}\) + 1) R = 5 cal/mole-k.

2) Diatomic gases : A molecule of diatomic gas has 5 degrees of freedom, 3 translational and 2 rotational i.e., f = 5
Therefore c_v = \(\frac{f}{2}\) R = \(\frac{5}{2}\) R = 5 cal/mole-k.
C_p = (\(\frac{f}{2}\) + 1) R = \(\frac{7}{2}\) R = 7cal/mole-k.

3) Polyatomic gases : Polytomic molecule has 3 trnaslational 3 rotational degrees of freedom, i.e,, f = 6
Therefore C_v = \(\frac{f}{2}\) R = 3R = 6 cal/mole-k.
C_p = (\(\frac{f}{2}\) + 1) = 4R = 8 cal/mole-k.

Section – C (2 × 8 = 16)

Note :

• Answer any TWO questions.
• Each question carries EIGHT marks.
• ALL are long answer type Questions.

Question 19.
Develop the notions of work and kinetic energy and show that it leads to work-energy theorem.
Consider a drop of mass 1.00 g falling from a height of 1.00 km. What is the work done by the gravitational force ? (Take g = 10 ms²)
Answer:
Given, m = 1.00g = 10^-3 kg; g = 10\(\frac{\mathrm{m}}{\mathrm{s}^2}\); h = 1.00 km = 10³km
w = mgh = 10^-3 × 10 × 10^-3 = 10 J.

Question 20.
Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period. What is seconds pendulum ?
Answer:
Let ‘S’ be the point of suspension of a simple pendulum. Let ‘l’ be its length, which is equal to the distance between the point of suspension and the centre of mass of the bob. Let ‘A’ be its mean position.

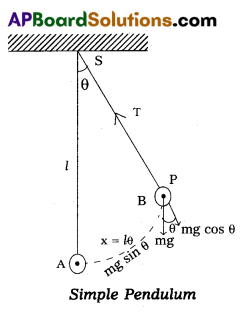
Let the simple pendulum be displaced through a small angle and released. Let the bob be in the position B at some instant.
AB = x = displacement from the mean position.
At B the forces acting on the bob are,
1) Weight ‘mg’ of the bob acting vertically downwards.
2) Tension ‘T’ in the string.

Weight can be resolved into two components, they are mg cosθ, mg sinθ.
mg cos θ balances the tension ‘T’ in the string.
The unbalanced component of mg is mg sin θ. This accelerates the bob towards the centre that is why it is known as restoring force.
∴ Restoring force F = – mg sin θ
∴ Acceleration a = \(\frac{\text { Force }}{\text { mass }}\) = \(\frac{-m g \sin \theta}{m}\)
= – g sin θ
If θ is small, then sin θ ≅ θ
∴ a = – gθ
But angle θ = \(\frac{\text { arc }}{\text { radius }}\) = \(\frac{x}{l}\)
a = -g \(\frac{x}{l}\)
a = -(\(\frac{g}{l}\))x → (1)
Since ‘g’ and ‘l’ are constants as, a ∝ – x
So the acceleration ∝ – displacement and it is directed towards mean position “O”. Hence it executes SHM.
The general equation for S.H.M. is
a = – ω²y → (2)
Comparing (1) and (2)
ω² = \(\frac{g}{l}\)
ω = \(\sqrt{\frac{g}{l}}\)
\(\frac{2 \pi}{T}\) = \(\sqrt{\frac{g}{l}}\)
T = \(\frac{2 \pi}{\sqrt{\frac{g}{l}}}\)
⇒ T = 2π\(\sqrt{\frac{l}{g}}\)
Where T is the time period of the simple pendulum.

Seconds pendulum : A pendulum whose time period is equal to 2 seconds is called seconds pendulum. It is used in pendulum clocks.
Its length changes with acceleration due to gravity.

Problem :
T = 2π\(\sqrt{\frac{l}{g}}\)
T = 2 sec, g = 9.8 m/s²
2 = 2π\(\sqrt{\frac{l}{g}}\)
l = \(\frac{\mathrm{g}}{\pi^2}\) = \(\frac{9.8}{(3.14)^2}\) = lm (or) 10 cm.

Question 21.
Explain reversible and irreversible processes. Describe the working of Carnot engine. Obtain an expression for the efficiency.
Answer:
Reversible process : A process that can be retraced back in the opposite direction in such away that the system passes through the same states as in the direct process, and finally the system and the surroundings return in their original states, is called a reversible process.
A reversible process is only a purely idealised process.

Examples :
i) Slow isothermal and slow adiabatic changes.
ii) Peltier effect and seeback effect.
iii) Fusion of ice and vaporisation of water.

Irreversible process : “A process that cannot be retraced back in the opposite direction” is called as irreversible process.
In this process the system does not pass through the same intermediate states as in the revesible process.
All natural processes such as conduction, radiation, radioactivity etc., the irreversible.

Example :
i) Work done against friction.
ii) Heat produced in conductors by passing a current through it. (Joule heating)
iii) Diffusion of gases.

Carnot Engine : A reversible heat engine operating between two temperatures is called a carnot engine. The cycle operating it is known as carnot’s cycle. In this cycle the working substance (say an ideal gas) is taken through a cycle by means of two isothermals and two adiabatics. The four operations are shown in P – V (indicator) diagram.

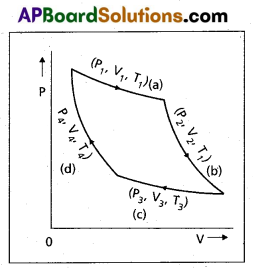
Step 1 → 2 : Isothermal expansion of the gas taking its state from (P₁, V₁, T₁) to (P₂, V₂, T₂). It is shown in curve (a).
The heat absorbed by the gas (Q₁) from the reservoir at temperature T₁ equals the workdone by the gas. i.e.
W_{1 → 2} = Q₁ = μRT₁
log_e \(\frac{V_2}{V_1}\) → (1)

Step 2 → 3 : Adiabatic expansion of the gas from (P₂, V₂, T₁) to
(P₃, V₃, T₂). It is shown in curve (b). The work done by the gas is given by
W_{2 → 3} = \(\frac{\mu R\left(T_1-T_2\right)}{(r-1)}\) → (2)

Step 3 → 4 : Isothermal compression of the gas from (P₃, V₃, T₂) to (P₄, V₄, T₂). It is shown in curve (c).
Heat released (Q₂) by the gas to the reservoir at temperature T₂ equals the work done on the goes.
i.e., W_{3 → 4} = μRT₂ log_e\(\frac{V_4}{V_3}\) = – μ RT₂ log_e\(\frac{V_3}{V_4}\)

Step _{4 → 1} : Adiabatic compression of the gas from (P₄, V₄, T₂) to (P₁, V₁, T₁). It is shown incurve (d).
W_{4 → 1} = μR \(\frac{\left(T_2-T_1\right)}{(r-1)}\) = – μR \(\frac{\left(T_1-T_2\right)}{(r-1)}\)
Total workdone by the gas in one complete cycle is
W = W_{1 → 2} + W_{2 → 3} + W_{3 → 4} + W_{4 → 1}