AP Inter 1st Year Physics Question Paper March 2020

Thoroughly analyzing AP Inter 1st Year Physics Model Papers and AP Inter 1st Year Physics Question Paper March 2020 helps students identify their strengths and weaknesses.

AP Inter 1st Year Physics Question Paper March 2020

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note:

• Answer All questions.
• Each question carries TWO marks.
• All are very short answer type questions.

Question 1.
What is the discovery of Sir. C.V. Raman ?
Answer:
In elastic scattering of light by molecules.

Question 2.
The percentage error in the mass and speed are 2% and 3% respectively. What is the maximum error in kinetic energy ?
Solution:
\(\frac{\Delta \mathrm{M}}{\mathrm{M}}\) × 100 = 2%, \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100 = 3%
Kinetic energy = \(\frac{1}{2}\) mV²
\(\frac{\Delta \mathrm{K}}{\mathrm{K}}\) × 100 = \(\frac{\Delta \mathrm{M}}{\mathrm{M}}\) × 100 + 2 \(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100
= 2 + 2(3) = 26 = 8%.

Question 3.
\(\vec{A}\) = \(\vec{i}\) + \(\vec{j}\). What is the angle between the vector and X – axis ?
Solution:
\(\vec{A}\) = \(\vec{i}\) + \(\vec{j}\)
cos α = \(\frac{A x}{|A|}\) (∵ A_x = 1)
= \(\frac{1}{\sqrt{1^2+1^2}}\) = \(\frac{1}{2}\)
α = cos^-1 (\(\frac{1}{2}\)) = 45°

Question 4.
Why does the car with a flattened tyre stop sooner than the one with the inflatted tyres ?
Answer:
Flattened deforms more than the inflated type. Due to greater deformation of the type colling friction is large hence it stops it stops soon.

Question 5.
Define Average Pressure. Mention its unit.
Answer:
Average pressure (P_av): Average power is defined as the normal force acting per unit area.
P_av = \(\frac{F}{A}\)
units → N / m² (or) pascal
Dimensional formula → [ML^-1 T^-1]
Pressure is a scalar quantity.

Question 6.
What are water proofing agents and water wetting agents ?
Answer:
Water proffing agents are added, to create a large angle of contact between water and fibres. Soaps, detergents and dying substances are wetting agents. When they are added, the angle of contact becomes small. So, that they may penetrate well and become effective.

Question 7.
State Newton’s law of cooling.
Answer:
The rate of loss of heat is directly proportional to the difference in temperature between the body and its surroundings provided the temperature difference is small, i.e., – \(\frac{\mathrm{dQ}}{\mathrm{dt}}\) α (T_B – T_S).

Question 8.
Ventilators are provided in rooms just below the roof. Why ?
Answer:
Ventilators are provided in rooms just below the roof, because the hot air escapes out and fresh air enters into the rooms due to convection.

Question 9.
Define mean free path.
Answer:
The average distance covered by a molecule between two successive collisions is called the mean free path.

Question 10.
State Boyle’s law and Charles’s law.
Answer:
Boyle’s law : At constant temperature, the pressure of a given mass of gas varies inversely with volume.
Charles law : At constant pressure, the volume of the gas is proportional to its obsolute temperature.

Section – B (6 × 4 = 24)

Note :

• Answer ANY SIX questions.
• Each question carries FOUR marks.
• All are very short answer type questions.

Question 11.
A car moving along a straight high way with speed of 126 km / h is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform) and how long does it take for the car to stop?
Solution:
Here, u = 126 km h^-1 = \(\frac{126 \times 1000}{60 \times 60}\) ms^-1
= 35 ms^-1; v = 0, S = 200 m, a = ?
and t = ?
We know
v² = u² + 2as
0 = (35)² + 2 × a × 200 (Or)
a = \(\frac{-(35)^2}{2 \times 200}\) = \(\frac{-49}{16}\)
= – 3.06 ms^-2
As v = u + at
0 = 35 + (\(\frac{-49}{16}\)) t(Or)
t = \(\frac{35 \times 16}{49}\) = \(\frac{80}{7}\) = 11.43s.

Question 12.
State parallelogram law of vectors. Derive an expression for the magnitude and direction of the resultant vector.
Answer:
Statement: If two vectors acting at a point are represented by the adjacent sides of a parallelogram in magnitude and direction, then their resultant is represented by the diagonal of the parallelogram in magnitude and direction drawn from the same point.

Explanation : Let two forces \(\overrightarrow{\mathrm{P}}\) and \(\overrightarrow{\mathrm{Q}}\) act at a point O. Let θ be the angle between two forces. Let the side OA = \(\overrightarrow{\mathrm{P}}\) and OB = \(\overrightarrow{\mathrm{Q}}\). The parallelogram OACB is compelted. The points O and C are joined. Now OC = \(\overrightarrow{\mathrm{R}}\)

Resultant magnitude :
in fig \(\overrightarrow{\mathrm{OA}}\) = \(\overrightarrow{\mathrm{P}}\), \(\overrightarrow{\mathrm{OB}}\) = \(\overrightarrow{\mathrm{Q}}\). \(\overrightarrow{\mathrm{OC}}\) = \(\overrightarrow{\mathrm{R}}\)
in the triangle COD, OC² = OD² + CD²
OC² = (OA + AD)² + CD² (∵ OD = OA + AD)
OC² = OA² + AD² + 2OA. AD + CD62²
OC² = OA² + AC² + 2OA. AD
From Δ^le CAD, AD² + CD² = AC²

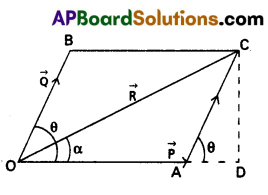
From Δ^leCAD, cos θ = \(\frac{A D}{A C}\) ………… (1)
AD = AC cos θ ………. (2)
∴ R² = p² + Q² + 2PQ cos θ
R= \(\sqrt{P^2+Q^2+2 P Q \cos \theta}\) …………… (3)

Resultant direction :
Let a be the angle made by the resultant vector with \(\overrightarrow{\mathrm{R}}\) with \(\overrightarrow{\mathrm{P}}\)
Then tan α = \(\frac{C D}{O D}\)
tan α = \(\frac{C D}{O A+A D}\) ………… (4)
In the triangle CAD, sin θ = \(\frac{C D}{A C}\)
CD = AC sin θ
CD = Q sin θ ………. (5)
tan α = (\(\frac{\mathrm{Q} \sin \theta}{\mathrm{P}+\mathrm{Q} \cos \theta}\)) (∵ AD – Q cos θ) ………… (6)
a = tan^-1\(\frac{\mathrm{Q} \sin \theta}{\mathrm{P}+\mathrm{Q} \cos \theta}\)

Question 13.
Define the terms momentum and impulse. State and explain the law of conservation of linear momentum. Give examples.
Answer:
Momentum : The product of mass and velocity of a body is
called momentum.,
momentum p = mv

Impulse : The product of force and time that produces finite change in momentum ofthe body is called impulse.
Impulse (l) = Force × time duration = mat = m \(\frac{(v-u)}{t}\)t
= (mv = mu)

Law of conservation of linear momentum : The total momentum of an isolated sysem of interacting particles remains constant, if there is no resultant external force acting on it.

Explanation : Consider two smooth, non – rotating spheres of masses m₁ and m₂ (m₁ > m₂). Let u₁ and u₂ be their initial velocities. Let v₁ and v₂ be final velocities after head on collision. According to law of conservation of linear momentum, we have Momentum ofthe system before collision = Momentum ofthe system after collision, i.e., m₁u₁ + m₂u₂ = m₁v₁+ m₂v₂
Examples :

1. Motion of a Rocket
2. Bullet – Gun motion.

Question 14.
Define vector product. Explain the properties of a vector product with two examples.
Answer:
The cross product of two vetors is given by \(\overrightarrow{\mathrm{C}}\) = \(\overrightarrow{\mathrm{A}}\) × \(\overrightarrow{\mathrm{B}}\) The magnitude of the vector defined from cross product of two vectors is equal to product of magnitudes of the vectors and sine of angle between the vectors.

Direction of the vectors is given by right hand corkscrew rule and is perpendicular to the plane containing the vectors.
∴ |\(\overrightarrow{\mathrm{C}}\)| = AB sin θ. and \(\overrightarrow{\mathrm{C}}\) = AB sin θ \(\begin{aligned}
& \Delta \\
& \mathrm{n}
\end{aligned}\). Where, \(\begin{aligned}
& \Delta \\
& \mathrm{n}
\end{aligned}\) is the unit vector perpendicular to the plane containing the vectors \(\overrightarrow{\mathrm{A}}\) and \(\overrightarrow{\mathrm{B}}\)

Example :

1. Torque is cross product of position vector and Force, i.e., \(\overrightarrow{\mathrm{T}}\) = \(\overrightarrow{\mathrm{r}}\) × \(\overrightarrow{\mathrm{F}}\)
2. Angular momentum is cross product of position vector and momentum i.e., \(\overrightarrow{\mathrm{L}}\) = \(\overrightarrow{\mathrm{r}}\) × \(\overrightarrow{\mathrm{p}}\)

Question 15.
The moment of inertia of a fly i.e., wheel making 300 revolutions per minute is 0.3kgm2. Find the torque required to bring it to rest in 20s.
Solution:
Here I = 0.3kg m²; \(\frac{N}{t}\) = \(\frac{300 \text { revolutions }}{1 \text { minute }}\)
ω_i = \(\frac{2 \pi N}{t}\) = 2π × \(\frac{300}{60}\) = 10π rad/s.
t = 20 S; W_f = 0; τ = ?
τ = I α = I = (\(\frac{\omega_f-\omega_i}{t}\))
∴ τ = 0.3 (\(\frac{0-10 \pi}{20}\)) = \(-\frac{0.3 \pi}{2}\) = – 0.471 Nm.

Question 16.
What is a Geostationary Satellite ? State it uses.
Answer:
Geo – Stationary satellite : If the period of revolution of an artificial satellite is equal to the period of rotation of earth, then such a satellite is called geo – stationary satellite.
Tjme period of geo – stationary satellite is 24 hours.

Uses :

1. Study the upper layers of atmosphere.
2. Fore most the changes in atmosphere.
3. Know the shape and size of the earth.
4. Identify the minerals and natural resources present inside and on the surface of the earth.
5. Transmit the T.V. programmes to distant objects
6. Under, take space research i.e., to know about the planets, satellites, comets etc.

Question 17.
Describe the behaviour of a wire under gradually increasing load.
Answer:
When the load is increased in steps, a graph is drawn between stress on y – axis and corresponding strain on x – axis.
1. Proportionality limit : In the. linear position OA, stress is proportional to strain i.e., Hookes law obeyed by the wire is up to point A. The graph is a straight line. Whenever the stretching force at A is removed. The wire regains its original length.

A is called proportionality limit.

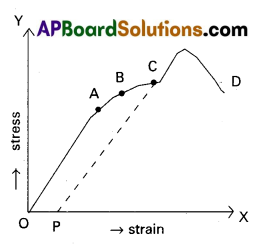
2. Elastic limit : In the graph B is the elastic limit. Through the wire doesnot obey Hooke’s law at B. The wire regains its original length after removing the stretching force at B. upto point B the wire is under elastic behaviour.

3. Permanent set (or) yield point : In the graph c is the yield point. If the stretching force at c is removed, the wire doesnot regain its original length and the length of the wire changes permanently. In this position the wire flows like a viscous liquid. After the point c, the wire is under plastic behaviour, c is called permanent set (or) yield point.

4. Breaking point : When the stress increased, the wire becomes thinner and thinner. When the stress increases to a certain limit the wire breaks. The stress at Which the Wire breaks is called breaking stress and the point D is called breaking point.

5. Elastic fatigue : The state of temporary loss Of elastic nature of a body due to continuous strain is called elastic fatigue. When a body is subjected to continuous strain within the elastic limit, it appears to have lost elastic property temporarily to some extent and becomes weak.

Question 18.
Explain conduction, convection and radiation with examples.
Answer:
The heat is transmitted in three types.
They are :
1) Conduction
2) Convection
3) Radiation.

1) Conduction : The process of transmission of heat from one place to other without actual movement of the particles of the medium is called conduction.
Ex : When long iron rod is heated at one end, heat transmits to the othr end.

2) Convection : The process of transmission of heat from one place to another by the actual movement of the particles is called convection.
Ex : If water in a beaker is heated, the particles of water at the bottom receive the heat first. These particles expand, become lighter and rise up. At the same time colder and denser particles reach the bottom. They get in their turn heated and move up. This process is known as convection.

3) Radiation : The process of transmission of heat from one place to another without any intervening medium is called radiation.
Ex : Earth receives heat radiations from the sun.

Section – C (2 × 8 = 16)

Note :

• Answer ANY TWO questions.
• Each question carries EIGHT marks.
• All are long answer questions.

Questio 19.
What are collisions ? Explain the possible types of collisions. Show that in the case of one dimensional elastic collision, the relative velocity of approach of two colliding bodies before collision is equal to the relative velocity of separation after collision.
Answer:
Collisions : A strong interactions between bodies that occurs for a very short interval during which redistribution of momenta occur ignoring the effect of other forces are called collisions.

Collisions are of two types :
i) Elastic collision : The collision in which both momentum and kinetic energy is constant is called elastic collision.

ii) Inelastic collision : The collision in which both momentum remains constant but not kinetic energy is called inelastic collision.

One dimensional elastic collision : Consider two spheres (bodies) which have smooth, non – rotating of masses m₁ and m₂ (m₁ > m₂) are moving along the straight line joining their centres of mass with initial velocities u₁ mand u₂ (u₁ > u₂). They undergo head on collision and move along the same line after collision with final velocities v₁ and v₂. These two bodies exert forces on each other during collision.
Hence, both momentum and kinetic energy are conserved. According to law of conservation of linear momentum.

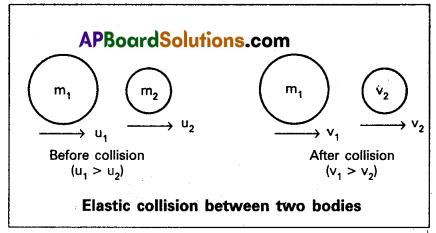
m₁u₁ + m₂ u₂ = m₁ v₁ + m₂ v₂, m₁ (u₁ – v₁) = m₂ (v₂ + u₂) ……. (1)
According to law of conservation of kinetic energy

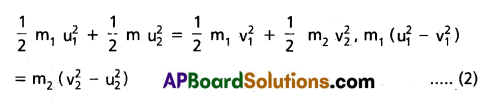
\(\frac{\text { equ (2) }}{\text { equ (1) }}\) = \(\frac{m_1\left(u_1-v_1\right)\left(u_1+v_1\right)}{m_1\left(u_1-v_1\right)}\) = \(\frac{m_2\left(v_2-u_2\right)\left(v_2+u_2\right)}{m_2\left(v_2-u_2\right)}\)
u₁ + v₁ = v₂ + u₂, u₁ – u₂ = v₂ = v₁ ……… (3)

From the above equation, in one dimensional elastic collision, the relative velocity of approach before collision is equal to the relative velocity of separation after collision.

From the equation (4), v₁ = v₂ – u₁ + u₂
Sub. this value in equation (1) we get
ml (u1 – v1) = m2 (u1 – u2 + v1 – u2), m1 u1 – m1v1 = m2 u1 – m2 u2 + m2 v1 – m2 u2
m1 u1 – m2 u1 + 2 m2 u2 = m1 v1 + m2 v1, (m1 – m2) u1 + 2 m2 u2 = (m1 + m2) u1
2m1u1 (nr^-m-,)
v₂ \(\frac{2 m_1 u_1}{\left(m_1+m_2\right)}\) + \(\frac{\left(m_2-m_1\right)}{\left(m_1+m_2\right)}\) u₂u

velocity of separation after collision :
Consider two spheres (bodies) which have smoothy non – rotating of masses m₁ and m₂ (m₁ > m₂) are moving along straight line joining the centres of mass with initial velocities u₁ and u₂ (u₁ > u₂). They undergo head on collision and move along the the same line after collision with final velocities of v₁ and v₂. There two bodies exert forces on each other during collision.

Let the collision be elastic, then both momentum and K. E are conserved.

According to law of conservation of linear momentum. Mo-mentum of the system before collision = Movementum of the system after collision,
m₁ u₁ + m₂ u₂ = m₁v₁ + m₁ v₂
m₁ (u₁ – v₁) = m₂ (v₂ – u₂) ………… (1)
According to law of conservation of kinetic energy, K.E of the system before collision = K.E of the system after collision.

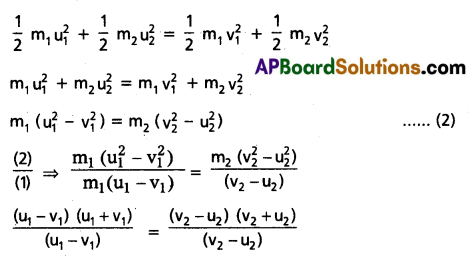
u₁ + v₁ = u₂ + v₂
u₁ + u₂ = v₂ + v₁
Relative velocity of approach from the above equation before collision = Relative velocity of separation after collision.

Question 20.
Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period. The mass and radius of a planet are double that of the earth, of the time period of a simple pendulum on the earth is T, find the time period on the planet.
Answer:

• consider simple pendulum, a small bob of mass m tied to an inextensible mass less string of length L and other end of the string is fixed from a rigid support.
• Once, the bob is slightly displaced and released, it begins to oscillate about mean position.
• Let θ be the angular displacement and T be the tension in the string.
• The forces acting on the bob are
  (a) tension T along the string
  (b) weight mg acts vertically downwards.
• The force mg can be resolved into two components
  1. mg cos θ along the PA and
  2. mg sin θ acts along PB.
• From figure at point P
  T = mg cos θ …………… (1)
• The force mg sin θ will provide the restoring torque, which tends to bring the bob back to its mean position O.
• The restoring torque is given by
  τ = Restoring force × ⊥^lar distance
  τ = – mg sin θ × L ………… (2)

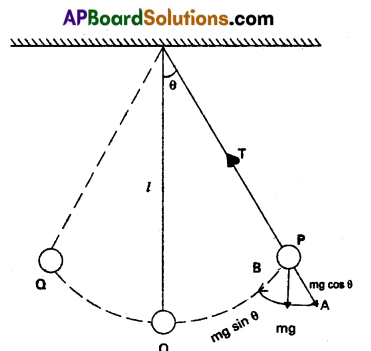
Here, negative sign showthat the torque acts to reduce θ.
Then sin θ is replaced by θ i.e., sin θ = θ
τ = – mg L θ ………… (3)
(∵ sin θ = θ – \(\frac{\theta^3}{3 !}\) + \(\frac{\theta^5}{5 !}\) …… )

• From equation (3), we note that τ ∝ θ and this τ will bring the bob back towards its equilibrium position.
  So, if the bob is left free, it will execute angular simple harmonic motion.
  Comparing equation (3), with the equation τ = – kθ, we have spring factor, k = mgL.
• Here inertia factor = Moment of inertia of the bob about the point of suspension = mL²
• In S.H.M, Time period (T) = 2π \(\sqrt{\frac{\text { Inertia factor }}{\text { Spring factor }}}\)
  T = 2π \(\sqrt{\frac{\mathrm{mL}^2}{\mathrm{mgL}}}\)
  T = 2π \(\sqrt{\frac{L}{g}}\) ……….. (4)
  Seconds pendulum : A pendulum whose time period is 2 seconds is called seconds pendulum.
  T = 2 seconds.
  The mass and radius of a planet are double that of the earth. If the time period of a simple pendulum on the earth is T, find the time period on the planet.
  g = \(\frac{G M}{R^2}\) ⇒ ∝ \(\frac{M}{R^2}\)
  g ∝ \(\frac{M}{R^2}\)
  

Question 21.
Describe the working of Carnot engine. Obtain an expression for the efficiency.
Answer:
Reversible process : A process that can be retraced back in the opposite direction in such away that the system passes through the same states as in the direct process, and finally the system and the surroundings return in their original states, is called a reversible process.

A reversible process is only a purely idealised process.
Examples :

1. Slow isothermal and slow adiabatic changes
2. Peltier effect and seeback effect.
3. Fusion of ice and vaporisation of water.

Irreversible process : “A process that cannot be retraced back in the opposite direction” is called as irreversible process.

In this process the system does not pass through the same intermediate states as in the reversible process. All natural processes such as conduction, radiation, radioactivity etc, are irreversible.

Example :

1. Work done against friction.
2. Heat produced in conductors by passing a current thorugh it. (joule heating)’
3. Diffusion of gases.

Carnot Engine : A reversible heat engine operating between two temperatures is called a carnot engine. The cycle operating it is known as carnot’s cycle. In this cycle the working substance (say an ideal gas) is taken through a cycle by means of two isothermals and two adiabatics. The four operations are shown in P – V (indicator) diagram.

Step 1 → 2 : Isothermal expansion of the gas taking its state from (P₁, V₁ T₁,) to (P₂, V₂, T). It is shown in curve (a)

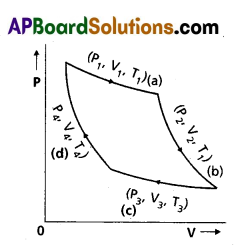
The heat absorbed by the gas (Q₁) from the reservoir at temperature T₁ equals the workdone by the gas. i.e.
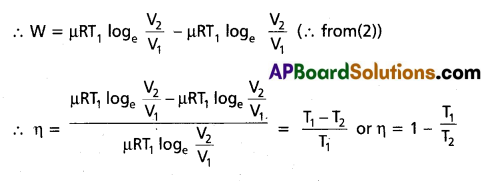
W_{1 → 2} = Q₁ = µRT₁log_e(\(\frac{V_2}{V_1}\)) ………….. (1)

Step 2 → 3 : Adiabatic expansion of the gas from (P₂, V₂, T₁,) to (P₃, V₃, T₂). It is shown in curve (b). The work done by the gas is given by
W_{2 → 3} = \(\frac{\mu R\left(T_1-T_2\right)}{(r-1)}\)

Step 3 → 4 : Isothermal compression of the gas from (P₃, V₃, T₂) to (P₄ , V₄, T₂). It is shown in curve (c). Heat released (Q₂) by the gas to the reservoir at temperature T equals the work done on the goes.
i.e., W_{3 → 4} = µRT₂log_e(\(\frac{V_4}{V_3}\)) = – µRT₂log_e(\(\frac{V_3}{V_4}\)

Step 4 → 1 : Adiabatic compression of the gas from (P₄ , V₄, T₂) to (P₁, V₁, T₁). It is shown in curve (d) Work done on the gas is given by.


A refrigerator is to mainain eatables kept inside at 9° C. If room temperature is 36° C, calculate the coefficient of performance.
Here
T₁ = 36°C = 36 + 273 = 309K
T₂ = 10°C = 10 + 273 = 283 K
COP = \(\frac{T_2}{T_1-T_2}\) = \(\frac{283}{309-283}\)
= \(\frac{283}{26}\) = 10.9