TS Inter 1st Year Maths 1A Question Paper May 2018

Thoroughly analyzing TS Inter 1st Year Maths 1A Model Papers and TS Inter 1st Year Maths 1A Question Paper May 2018 helps students identify their strengths and weaknesses.

TS Inter 1st Year Maths 1A Question Paper May 2018

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer ALL questions.
• Each question carries TWO marks.

Question 1.
If f: R – {0} → R is defined by f(x) = x³ – \(\frac{1}{x^3}\), then show that f(x) + f(\(\frac{1}{x}\)) = 0.
Solution:

Question 2.
Find the domain of the real valued function f(x) = \(\frac{1}{\left(x^2-1\right)(x+3)}\).
Solution:
Given f(x) = \(\frac{1}{\left(x^2-1\right)(x+3)}\)
(x² – 1) (x + 3) ≠ 0
⇒ (x + 1) (x – 1) (x + 3) ≠ 0
⇒ x ≠ -1, x ≠ 1, x ≠ -3
∴ Domain of f = R – [-3, -1, 1]

Question 3.
If \(\left[\begin{array}{cc}
x-3 & 2 y-8 \\
z+2 & 6
\end{array}\right]=\left[\begin{array}{rr}
5 & 2 \\
-2 & a-4
\end{array}\right]\), then find the values of x, y, z and a.
Solution:
Given \(\left[\begin{array}{cc}
x-3 & 2 y-8 \\
z+2 & 6
\end{array}\right]=\left[\begin{array}{rr}
5 & 2 \\
-2 & a-4
\end{array}\right]\)
x – 3 = 5 ⇒ x = 8
2y – 8 = 2 ⇒ 2y = 10 ⇒ y = 5
z + 2 = -2 ⇒ z = -4
6 = a – 4 ⇒ a = 10
∴ x = 8, y = 5, z = -4, a = 10

Question 4.
If A = \(\left[\begin{array}{rrr}
-1 & 2 & 3 \\
2 & 5 & 6 \\
3 & x & 7
\end{array}\right]\) is a symmetric matrix, then find x.
Solution:
Given A = \(\left[\begin{array}{rrr}
-1 & 2 & 3 \\
2 & 5 & 6 \\
3 & x & 7
\end{array}\right]\)
Since A is a symmetric matrix.
∴ A^T = A
\(\left[\begin{array}{rrr}
-1 & 2 & 3 \\
2 & 5 & x \\
3 & 6 & 7
\end{array}\right]=\left[\begin{array}{rrr}
-1 & 2 & 3 \\
2 & 5 & 6 \\
3 & x & 7
\end{array}\right]\)
∴ x = 6

Question 5.
If the vectors \(-3 \vec{i}+4 \vec{j}+\lambda \vec{k}\) and \(\mu \vec{i}+8 \vec{j}+6 \vec{k}\) are collinear vectors, then find λ and µ.
Solution:

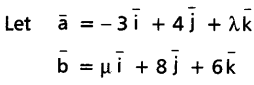
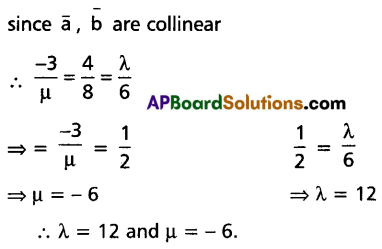
Question 6.
Find the vector equation of the plane passing through the points \(\vec{i}-2 \vec{j}+5 \vec{k},-5 \vec{j}-\vec{k}\) and \(-3 \vec{i}+5 \vec{j}\).
Solution:

Question 7.
Find the angle between the planes \(\vec{r} \cdot(2 \vec{i}-\vec{j}+2 \vec{k})\) = 3 and\(\vec{r} \cdot(3 \vec{i}+6 \vec{j}+\vec{k})\) = 4.
Solution:

Question 8.
If a cos θ – b sin θ = c, then show that a sin θ + b cos θ = ±\(\sqrt{a^2+b^2-c^2}\).
Solution:
Given a cos θ – b sin θ = c
Let a sin θ + b cos θ = λ
By squaring and adding, we get
(a cos θ – b sin θ)² + (a sin θ + b cos θ)² = c² + λ²
⇒ a² cos²θ – 2ab sin θ cos θ + b² sin²θ + a² sin²θ + 2ab sin θ cos θ + b² cos²θ = c² + λ²
⇒ a² (cos²θ + sin²θ) + b² (sin²θ + cos²θ) = c² + λ²
⇒ a² (1) + b² (1) = c² + λ²
⇒ a² + b² = c² + λ²
⇒ λ² = a² + b² – c²
⇒ λ = ±\(\sqrt{a^2+b^2-c^2}\)
∴ a sin θ + b cos θ = ±\(\sqrt{a^2+b^2-c^2}\)

Question 9.
Find the minimum and maximum values of 3 cos x + 4 sin x.
Solution:
Let f(x) = 3 cos x + 4 sin x
Here a = 3, b = 4, c = 0.
Minimum value of f(x) = c – \(\sqrt{a^2+b^2}\)
= 0 – \(\sqrt{9+16}\)
= 0 – \(\sqrt{25}\)
= -5
Maximum value of f(x) = c + \(\sqrt{a^2+b^2}\)
= 0 + \(\sqrt{9+16}\)
= 0 + \(\sqrt{25}\)
= 5

Question 10.
Show that \(\tan h^{-1}\left(\frac{1}{2}\right)=\frac{1}{2} \log _e^3\).
Solution:

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Answer ANY FIVE questions.
• Each question carries FOUR marks.

Question 11.
If 3A = \(\left[\begin{array}{rrr}
1 & 2 & 2 \\
2 & 1 & -2 \\
-2 & 2 & -1
\end{array}\right]\), then show that A^-1 = A’.
Solution:

Question 12.
a, b, c are non-coplanar vectors. Prove that the following four points are coplanar:
-a + 4b – 3c, 3a + 2b – 5c, -3a + 8b – 5c, -3a + 2b + c.
Solution:

Question 13.
The vectors AB = \(3 \vec{i}-2 \vec{j}+2 \vec{k}\) and AD = \(\vec{i}-2 \vec{k}\) represent the adjacent sides of a parallelogram ABCD. Find the angle between the diagonals.
Solution:

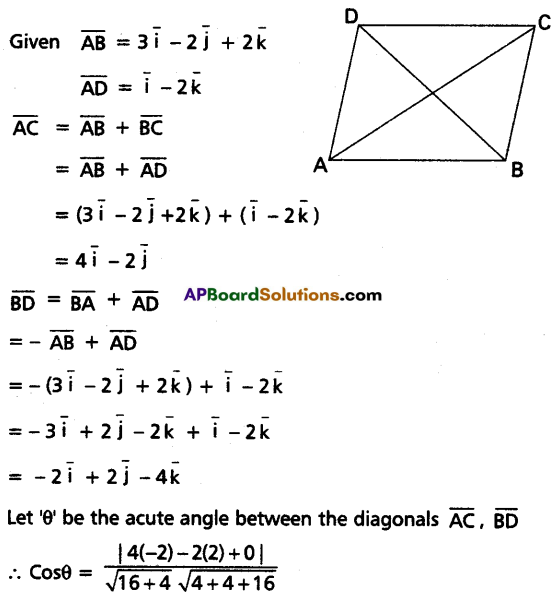
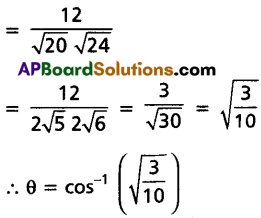
Question 14.
Show that \(\cos ^4\left(\frac{\pi}{8}\right)+\cos ^4\left(\frac{3 \pi}{8}\right)+\cos ^4\left(\frac{5 \pi}{8}\right)+\cos ^4\left(\frac{7 \pi}{8}\right)=\frac{3}{2}\).
Solution:


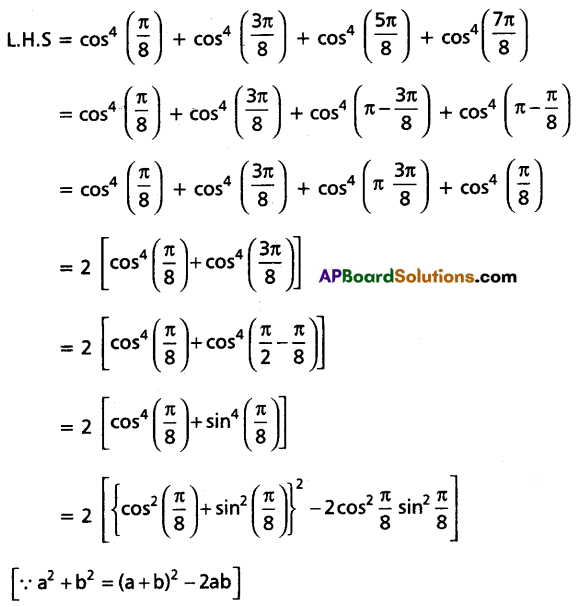
= R.H.S
∴ L.H.S = R.H.S
∴ \(\cos ^4\left(\frac{\pi}{8}\right)+\cos ^4\left(\frac{3 \pi}{8}\right)+\cos ^4\left(\frac{5 \pi}{8}\right)+\cos ^4\left(\frac{7 \pi}{8}\right)=\frac{3}{2}\)

Question 15.
Solve 2 cos²θ – √3 sin θ + 1 = 0.
Solution:
Given 2 cos²θ – √3 sin θ + 1 = 0
⇒ 2(1 – sin²θ) – √3 sin θ + 1 = 0
⇒ 2 – 2 sin²θ – √3 sin θ + 1 = 0
⇒ -2 sin²θ – √3 sin θ + 3 = 0
⇒ 2 sin²θ + √3 sin θ – 3 = 0
⇒ 2 sin²θ + 2√3 sin θ – √3 sin θ – 3 = 0
⇒ 2 sin θ (sin θ + √3) – √3 (sin θ + √3 ) = 0
⇒ (sin θ + √3) (2 sin θ – √3) = 0
since sin θ + √3 ≠ 0
∴ 2 sin θ – √3 = 0
⇒ 2 sin θ = √3
⇒ sin θ = \(\frac{\sqrt{3}}{2}\) = sin \(\frac{\pi}{3}\)
∴ θ = nπ + (-1)ⁿ \(\frac{\pi}{3}\), n ∈ z
∴ Solution set x = [nπ + (-1)ⁿ \(\frac{\pi}{3}\)/n ∈ z]

Question 16.
Solve the following equation for x:
\(3 \sin ^{-1}\left(\frac{2 x}{1+x^2}\right)-4 \cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)+2 \tan ^{-1}\left(\frac{2 x}{1-x^2}\right)=\frac{\pi}{3}\)
Solution:

Question 17.
If sin θ = \(\frac{a}{b+c}\), then show that cos θ = \(\frac{2 \sqrt{b c}}{b+c} \cos \frac{A}{2}\).
Solution:

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Answer ANY FIVE questions.
• Each question carries SEVEN marks.

Question 18.
If f = {(4, 5), (5, 6), (6, -4)} and g = {(4, -4), (6, 5), (8, 5)} then find:
(i) f + g
(ii) 2f + 4g
(iii) f + 4
(iv) \(\frac{f}{g}\)
(v) \(\sqrt{f}\)
(vi) f²
(vii) |f|
Solution:
Given f = [(4, 5), (5, 6), (6, -4)]
g = [(4, -4), (6, 5), (8, 5)]
∴ Domain of f = [4, 5, 6]
Domain of g = [4, 6, 8]
∴ The domain of f ∩ g = [4, 6]
(i) (f + g) (4) = f(4) + g(4)
= 5 + (-4)
= 1
(f + g) (6) = f(6) + g(6)
= -4 + 5
= 1
∴ f + g = [(4, 1), (6, 1)]
(ii) (2f + 4g) (4) = 2f(4) + 4g(4)
= 2(5) + 4(-4)
= 10 – 16
= -6
(2f + 4g) (6) = 2f(6) + 4g(6)
= 2(-4) + 4(5)
= -8 + 20
= 12
∴ 2f + 4g = [(4, – 6), (6,12)]
(iii) (f + 4) (4) = f(4) + 4
= 5 + 4
= 9
(f + 4) (5) = f(5) + 4
= 6 + 4
= 10
(f + 4) (6) = f(6) + 4
= -4 + 4
= o
∴ f + 4 = [(4, 9), (5, 10), (6, 0)]

(vi) f²(4) = [f(4)]² = 5² = 25
f²(5) = [f(5)]² = 6² = 36
f²(6) = [f(6)]² = (-4)² = 16
∴ f² = [(4, 25), (5, 36), (6, 16)]
(vii) |f|(4) = |f(4)| = |5| = 5
|f| (5) = |f(5)| = |6| = 6
|f| (6) = |f(6)| = |-4| = 4
|∴ f| = [(4, 5), (5, 6), (6, 4)]

Question 19.
Show that ∀ n ∈ N, 12 + (1² + 2²) + (1² + 2² + 3²) + ……. upto n terms = \(\frac{n(n+1)^2(n+2)}{12}\) by Mathematical Induction.
Solution:
The nth term of the given series is (1² + 2² + 3² + …….. + n²)
Let p(n) be the statement:
1² + (1² + 2²) + (1² + 2² + 3²) + …… + (1² + 2² + ……. + n²) = \(\frac{n(n+1)^2(n+2)}{12}\)
and the sum on the L.H.S. is denoted by S(n).
Since s(1) = 1² = \(\frac{1(1+1)^2(1+2)}{12}\) = 1 = 1²
∴ p(1) is true.
Assume that the statement is true for n = k
(i.e.,) S(k) = 1² + (1² + 2²) + …… + (1² + 2² + ….. + k²) = \(\frac{k(k+1)^2(k+2)}{12}\)
We show that S(k + 1) = \(\frac{(k+1)(k+2)^2(k+3)}{12}\)
We observe that
S(k + 1) = 1² + (1² + 2²) + …… + (1² + 2² + 3² + …… + k²) + [1² + 2² + ……. + k² + (k + 1)²]
= S(k) + [1² + 2² + ……. + k² + (k + 1)²]
= \(\frac{k(k+1)^2(k+2)}{12}\) + [1² + 2² + ……. + k² + (k + 1)²]


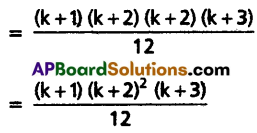
∴ The statement holds for n = k + 1.
∴ By the principle of mathematical induction, p(n) is true for all n ∈ N.
(i.e.,) 1² + (1² + 2²) + (1² + 2² + 3²) + ……. + (1² + 2² + …… + n²) = \(\frac{n(n+1)^2(n+2)}{12}\)

Question 20.
Show that \(\left|\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right|^2=\left|\begin{array}{ccc}
2 b c-a^2 & c^2 & b^2 \\
c^2 & 2 a c-b^2 & a^2 \\
b^2 & a^2 & 2 a b-c^2
\end{array}\right|\) = (a³ + b³ + c³ – 3abc)²
Solution:

Question 21.
Solve the following system of equations x – y + 3z = 5, 4x + 2y – z = 0, -x + 3y + z = 5 by Cramer’s rule.
Solution:
Given
x – y + 3z = 5
4x + 2y – z = 0
-x + 3y + z = 5
Given system of equations can be written as AX = B

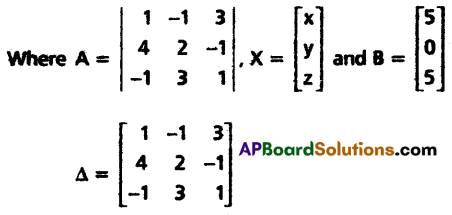
= 1(2 + 3) – (-1) (4 – 1) + 3(12 + 2)
= 5 + 3 + 42
= 50
Δ₁ = \(\left|\begin{array}{rrr}
5 & -1 & 3 \\
0 & 2 & -1 \\
5 & 3 & 1
\end{array}\right|\)
= 5(2 + 3) – (-1) (0 + 5) + 3(0 – 10)
= 25 + 5 – 30
= 0
Δ₂ = \(\left|\begin{array}{rrr}
1 & 5 & 3 \\
4 & 0 & -1 \\
-1 & 5 & 1
\end{array}\right|\)
= 1(0 + 5) – 5(4 – 1) + 3(20 + 0)
= 5 – 15 + 60
= 50
Δ₃ = \(\left|\begin{array}{rrr}
1 & -1 & 5 \\
4 & 2 & 0 \\
-1 & 3 & 5
\end{array}\right|\)
= 1(10 – 0) – (-1) (20 + 0) + 5(12 + 2)
= 10 + 20 + 70
= 100
x = \(\frac{\Delta_1}{\Delta}=\frac{0}{50}\) = 0
y = \(\frac{\Delta_2}{\Delta}=\frac{50}{50}\) = 1
z = \(\frac{\Delta_3}{\Delta}=\frac{100}{50}\) = 2
∴ x = 0, y = 1, z = 2

Question 22.
If \(\vec{a}=\vec{i}-2 \vec{j}+\vec{k}, \vec{b}=2 \vec{i}+\vec{j}+\vec{k}, \vec{c}=\vec{i}+2 \vec{j}-\vec{k}\), find \(\vec{a} \times(\vec{b} \times \vec{c})\) and \(|(\vec{a} \times \vec{b}) \times \vec{c}|\).
Solution:

Question 23.
If A, B, C are angles in a triangle, then prove that cos A + cos B – cos C = -1 + 4 \(\cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\).
Solution:
Given A + B + C = 180°
⇒ \(\frac{A}{2}+\frac{B}{2}+\frac{C}{2}\) = 90°
L.H.S = cos A + cos B – cos C


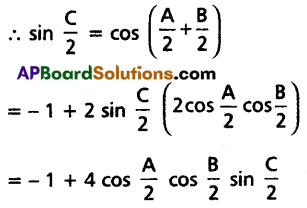
= R.H.S
∴ L.H.S = R.H.S
∴ cos A + cos B – cos C = -1 + 4 \(\cos \frac{A}{2} \cos \frac{B}{2} \sin \frac{C}{2}\).

Question 24.
In ΔABC, if r₁ = 8, r₂ = 12, r₃ = 24, find a, b, c.
Solution:
Given r₁ = 8, r₂ = 12, r₃ = 24

Δ = rs
⇒ 96 = 4s
⇒ s = 24
r₁ = \(\frac{\Delta}{s-a}\)
⇒ s – a = \(\frac{\Delta}{r_1}\)
⇒ 24 – a = \(\frac{96}{8}\)
⇒ 24 – a = 12
⇒ a = 12
r₂ = \(\frac{\Delta}{s-b}\)
⇒ s – b = \(\frac{\Delta}{r_2}\)
⇒ 24 – b = \(\frac{96}{12}\)
⇒ 24 – b = 8
⇒ b = 16
r₃ = \(\frac{\Delta}{s-c}\)
⇒ s – c = \(\frac{\Delta}{r_3}\)
⇒ s – c = \(\frac{96}{24}\)
⇒ 24 – c = 4
⇒ c = 20
∴ a = 12, b = 16, c = 20