AP Inter 1st Year Physics Question Paper March 2019

Thoroughly analyzing AP Inter 1st Year Physics Model Papers and AP Inter 1st Year Physics Question Paper March 2019 helps students identify their strengths and weaknesses.

AP Inter 1st Year Physics Question Paper March 2019

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer all questions.
• Each question carries two marks.
• All are very short answer type questions.

Question 1.
What is the discovery of C.V. Raman ?
Answer:
The elastic scattering of light by molecules.

Question 2.
The error in measurement of radius of a sphere is 1%. What is the error in the measurement of volume ?
Answer:
Radius of the sphere = \(\frac{\Delta r}{r}\) × 100 = 1%
Volume (V) = \(\frac{4}{8}\) × πr³
\(\frac{\Delta \mathrm{V}}{\mathrm{V}}\) × 100 = 3 × \(\frac{\Delta r}{r}\) × 100
= 3 × 1% = 3%.

Question 3.
The vertical component of a vector is equal to its horizontal component. What is the angle made by vector with X-axis ?
Answer:
The horizontal component is equal to the vertical component of a vector.
F cos θ = F sin θ.
tan θ = 1
θ = tan^-1(1) = 45°.

Question 4.
What is inertia ? What gives the measures of inertia ?
Answer:
The resistance of the body to change its state of rest or state of uniform motion in a straight line is called inertia of the body.
Acceleration = \(\frac{\text { Force }}{\text { Mass }}\)
∴ The more is the mass, less is the acceleration and more is the inertia. The mass of a body is a quantitative measure of its inertia.

Question 5.
What is the principle behind the carburettor of an automobile ?
Answer:
The carburettor of automobile has a venturi channel (nozzle) through which air flows with a large speed. The pressure is then lowered at the narrow neck and the petrol is sucked up in the chamber to provide the correct mixture of air to fuel necessary for combustion.

Question 6.
Give the expression for the excess pressure in an air bubble inside the liquid.
Answer:
Excess pressure in an air bubble inside the liquid, P_i – P_o = \(\frac{2 s}{r}\)
where s = Surface tension
r = Radius of the air bubble.
Air bubble forms inside the liquid, hence it has one liquid surface.

Question 7.
What are the lower and upper fixing points in Celsius and Fahrenheit scales ?
Answer:
In Celsius scale, lower fixed point is ice point or 0°C and upper fixed point is steam point or 100°C.
In Fahrenheit scale, lower fixed point is 32°F and upper fixed point is 212°F.

Question 8.
Why gaps are left between rails on a railway track ?
Answer:
The length of the rails increases in summer due to high temperature. Therefore’a gap is left to allow this expansion.

Question 9.
Define mean free path.
Answer:
The average distance covered by a molecule between two successive collision is called the mean free path.

Question 10.
When does a real gas behave like an ideal gas ?
Answer:
At low pressures and high temperatures real gases behave like an ideal gas.

Section – B (6 × 4 = 24)

Note :

• Answer any six of the following questions.
• Each question carries four marks.
• All are short answer type questions.

Question 11.
A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 kmh^-1. Finding the market closed, he instantly turns and walks back home with a speed of 7.5 kmh^-1. What is the (a) magnitude of average velocity and (b) average speed of the man over the time interval 0 to 50 minutes ?
Answer:
From home to market:
X₁ = 2.5 km; v₁ = 5 km h^-1;
t₁ = \(\frac{X_1}{v_1}\) = \(\frac{2.5}{5}\) = \(\frac{1}{2}\)h = 30 min.

From market to home :
X₂ = 2.5 km; v₂ = 5 km h^-1;
t₂ = \(\frac{X_2}{v_2}\) = \(\frac{2.5}{7.5}\) = \(\frac{1}{3}\)h = 20 min.

a) Magnitude of average velocity
= \(\frac{\Delta X}{\Delta t}\) = \(\frac{X_1-X_2}{t_1+t_2}\) = \(\frac{2.5-2.5}{50}\) = 0

b) Average speed
= \(\frac{X_1+X_2}{t_1+t_2}\) = \(\frac{2.5-2.5}{(30+20) \min }\) = \(\frac{5 \mathrm{~km}}{50 \times \frac{\mathrm{h}}{60}}\)
= 6 km h^-1.

Question 12.
Explain the terms the average velocity and instantaneous velocity. When they are equal ?
Answer:
Average velocity : The average velocity of the particle is defined as the ratio of displacement (Δx) to the time interval Δt
\(\bar{v}=\frac{\Delta x}{\Delta t}=\frac{x_2-x_1}{t_2-t_1}\)
Average velocity is independent of the path followed by the particle between the initial and final positions. It gives the result of the motion.

Instantaneous velocity :
The velocity of a particle at a particular instant of time is known as instantaneous velocity.
V = \({Lim}_{\Delta x \rightarrow 0} \frac{\Delta x}{\Delta t}\)
The instantaneous velocity may be positive (or) negative in straight line motion.
In uniform motion the instantaneous velocity of a body is equal to the average velocity.

Question 13.
State Newton’s second law of motion. Hence derive the equation of motion F = ma from it.
Answer:
Newton’s Second law of motion : “The rate of change of momentum of a body is directly proportional to the external force applied and takes place in the same direction”.
To show F = ma : Let a body of mass ‘m’ moving with a velocity ‘v’ under the action of an external force F in the direction of velocity.
Momentum ‘P’ of a body is the product of the mass and velocity V.
∴ P = mv ………… (1)
According to Newton’s second law of motion, we have
\(\frac{d p}{d t}\) ∝ F, where F = external force
(or) F = K\(\frac{d p}{d t}\) …………. (2)
From equations (1) and (2) we have
d(mv) m dv
F = K\(\frac{\mathrm{d}(\mathrm{mv})}{\mathrm{dt}}\) = K.m \(\frac{d v}{d t}\)
= Kma ……….. (3)
Since the rate of change of velocity \(\frac{d v}{d t}\) is the acceleration ‘a’ of the body.
In SI system the unit of force is Newton and is defined as that force Which when acting on a body of mass 1 kg produces in it an acceleration of 1 ms^-2.
i.e., from equation (3),
If F = 1, m = 1 and a = 1
we get K = 1
Hence F = \(\frac{d p}{d t}\) = ma
∴ F = ma

Question 14.
Define angular velocity (ω). Derive v = rω.
Answer:
Angular velocity (ω): The rate of change of angular displacement of a body is called angular velocity, i.e., ω = \(\frac{\mathrm{d} \theta}{\mathrm{dt}}\)

Derivation of v = rω : Consider a rigid body be moving with uniform speed (v)along the circumference of a circle of radius r. Let the body be displaced from A to B in a small interval of time Δt making an angle Δθ at the centre. Let the linear displacement be Δx from A to B.
From the property of circle, length of arc = radius x angle
Δx = r Δθ

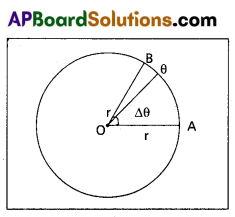
This equation is divided by Δt, and taking
Limit Δt -> 0 on both sides. We get \({Lt}_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}=r \underset{\Delta t \rightarrow 0}{{Lt}} \frac{\Delta \theta}{\Delta t}\)
But \({Lt}_{\Delta t \rightarrow 0} \frac{\Delta x}{\Delta t}\) = v and \({Lt}_{\Delta t \rightarrow 0} \frac{\Delta \theta}{\Delta t}\) = ω
∴ v = rω

Question 15.
Define angular acceleration and torque. Establish the relation between angular acceleration torque.
Answer:
Angular acceleration : The rate of change of angular velocity is called angular acceleration.
i.e., α = \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\)

Torque : The rate of change of angular momentum is called torque or the moment of force is called torque.

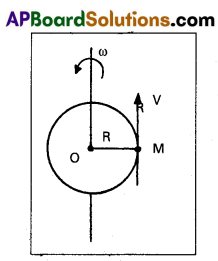
Relation between angular acceleration and torque : Consider a rigid body of mass ‘M’ rotating in a circular path of radius ‘R’ with angular velocity ‘ωω’ about fixed axis.

By defination, τ = \(\frac{\mathrm{dL}}{\mathrm{dt}}\) = \(\frac{\mathrm{d}(\mathrm{I} \omega)}{\mathrm{dt}}\)
Where I = MR² = moment of inertia of a body
t = I \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\) [∵ I = constant]
But \(\frac{\mathrm{d} \omega}{\mathrm{dt}}\) = ∝ ∴ τ = Iα

Question 16.
What is escape velocity ? Obtain an expression for it.
Answer:
Escape velocity : It is the minimum velocity with which a body should be projected, so that it moves into the space by overcoming the earth’s gravitational field.

Expression for escape velocity : Consider a body of mass m thrown with a velocity v_e
Then K.E = \(\frac{1}{2}\) m v_e² → (1)
The gravitational force of attraction of the earth of mass M and Radius R on a body of mass m at its surface is F = \(\frac{G M m}{R^2}\) → (2)
Gravitational P. E. = work done on the body
∴ P. E. = F × R = \(\frac{G M m}{R^2}\) × R
P. E. = \(\frac{G M m}{R}\) → (3)
A body just escapes when its K. E. = P. E

∴ Escape velocity is √2 times the orbital velocity.

Question 17.
Define stress and explain the types of stress.
Answer:
Stress : The restoring force per unit area is called stress
∴ Stress = \(\frac{\text { Restoring Force }}{\text { Area }}\) = \(\frac{F}{A}\)

Stress is classified into three types :
1) Longitudinal stress
2) Volume (or) Bulk stress
3) Tangential (or) shearing stress

1. Longitudinal stress (or) Linear stress : When a normal stress changes the length of a body, then it is called longitudinal stress.
Longitudinal stress = \(\frac{F}{A}\).

2. Volume (or) Bulk stress : When a normal stress changes the volume of a body, then it is called volume stress.
Volume stress = \(\frac{\text { Force }}{\text { Area }}\) = pressure.

3. Tangential (or) shearing stress : When the stress is tangential to the surface due to the application of forces parallel to the surface, then the stress is called tangential stress.
Tangential stress = \(\frac{F}{A}\) .

Question 18.
Explain conduction, convection and radiation with examples.
Answer:
The heat is transmitted in three types.
They are :
1) Conduction
2) Convection
3) Radiation.

1) Conduction : The process of transmission of heat from one place to other without actual movement of the particles of the medium is called conduction.
Ex : When long iron rod is heated at one end, heat transmits to the other end.

2) Convection : The process of transmission of heat from one place to another by the actual movement of the particles is called convection.
Ex. : If water in a beaker is heated, the particles of water at the bottom receive the heat first. These particles expand, become lighter and rise up. At the same time colder and denser particles reach the bottom. They get in their turn heated and move up. This process is known as convection.

3) Radiation : The process of transmission of heat from one place to another without any intervening medium is called radiation.
Ex. : Earth receives heat radiations from the sun.

Section – C (2 × 8 = 16)

Note :

• Answer any two of the following questions.
• Each question carries eight marks.
• All are long answer type questions.

Question 19.
What are collisions ? Explain the possible types of collisions, develop the theory of one dimensional elastic collision.
Answer:
Collisions : A strong interactions between bodies that occurs for a very short interval during which redistribution of momenta occur ignoring the effect of other forces are called collisions.

Collisions are of two types :
i) Elastic collision : The collision in which both momentum and kinetic energy is constant is called elastic collision.
ii) Inelastic collision : The collision in which momentum remains constant but not kinetic energy is called Inelastic collision.

Elastic collision in one dimension : Consider two spheres (bodies) which have smooth, non-rotating of masses m₁ and m₂(m₁ > m₂) are moving along the straight line joining their centres of mass with initial velocities u₁ and u₂ (u₁ > u₂).’They undergo head on collision and move along the same line after collision with final velocities v₁ and v₁. These two bodies exert forces on each other during collision.

Hence both momentum and kinetic energy are conserved. According to law of conservation of linear momentum.

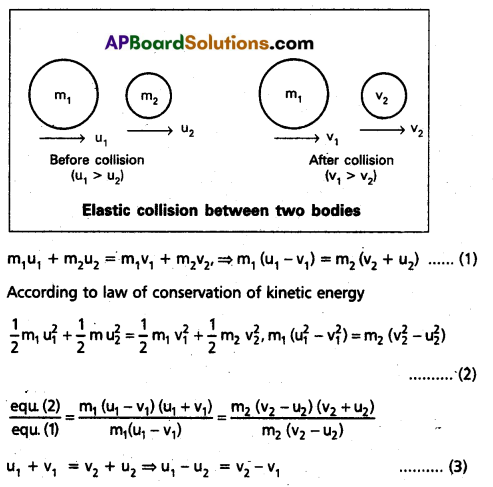
From the above equation, in one dimensional elastic collision, the relative velocity of approach before collision is equal to the relative velocity of separation after collision.
From equation (3) u₁ – u₂ = – v₁ + v₂, v₂ = u₁ – u₂ + v₁ …….. (4)
Sub equation (4) in equation (1) we get

Question 20.
a) Define simple harmonic motion. Show that the motion of (point) projection of a particle performing uniform circular motion, on any diameter, is simple harmonic.
b) On an average a human heart is found to beat 75 times in a minute. Calculate its frequency and period.
Answer:
“A body is said to be in simple harmonic motion, if it moves to and fro along a straight line, about its mean position such that, at any point its acceleration is directly proportional to its displacement in magnitude but opposite in direction and is directed always towards the mean position.

If ‘a’ is the acceleration of the body at any given displacement y from the mean position, then for the body to be in S.H.M.
a ∝ – y or a = – ky

When ‘k’ is constant of proportionality. (-) indicates that ‘a’ and ‘y’ are always in opposite directions.

To show that the projection of uniform circular motion on any diameter is simple harmonic : Consider a particle P moving on the circumference of a circle of radius A with uniform angular velocity ω. Let O be the centre of the circle. XX’ and YY’ are two mutually perpendicular diameters of the circle as shown in the figure. Let PN be drawn perpendicular to the diameter YV from P. As P moves on the circumference of the circle, N moves on the diameter YY’ to and fro about the centre O.

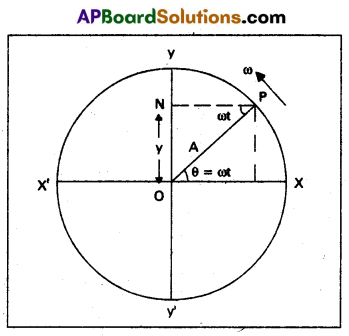
Let us consider the position of N at any time t, after leaving the point ‘O’, during its motion. The corresponding angular displacement of the particle P is ∠XOP = θ = ωt.
From Δ^le ONP, sin ωt = \(\frac{O N}{O P}\)
ON = OP sirt ωt (∵ ON = y, OP = A)
y = A sin ωt ______ (1)
Differentiating equation (1) w.r.t 1′, we get velocity

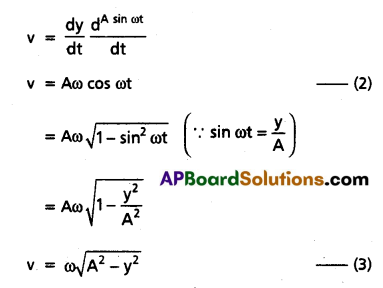
Again differentiating equation (2) w.r.t t, we get acceleration
a = \(\frac{d v}{d t}=\frac{d^{(A \omega \cos \omega t)}}{d t}\)
a = Aω²sin ωt (∵ A sin ωt)
a = ω²y ______ (4)
From equation (4) a ∝ – y ______ (5)
Hence acceleration is directly proportional to the displacement and opposite direction. Hence motion of N is simple harmonic.

b) On an average a human heart is found to beat 75 times in a minute. Calculate its frequency and period. .
Solution:
The beat frequency of heart = 75/(1 min)
= 75/(60 s)
= 1.25 H₂
The time period T = \(\frac{60}{75}\)
= 0.8 s.

Question 21.
State Second law of thermodynamics. How is heat engine different from a refrigerator?
Answer:
Second law of thermodynamics gives the direction of flow of heat. Second law consists two statements.
1) Kelvin – Planck statement: “No process is possible whose sole result is the absorption of heat from a reservoir and the complete conversion of the heat into work”.
(or)
“It is impossible to derive a continuous supply of engines in cooling a body below the coldest of its surroundings”.

2) Clausius statement: “No process is possible whose sole result is the transfer of heat from a colder object to a hotter object”.
(or)
“Heat cannot itself flow from cold body to hot body”.
Heat engine : A device which converts heat energy into work is called heat engine.
A heat engine consists of the essential parts.

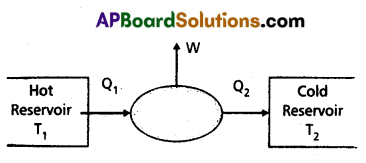
1) Source or hot reservoir : It is maintained at a very high temperature T₁ Heat is extracted from this body.

2) Working substance : In a steam engine working substance is steam. In diesel engine working substance is mixture of fuel vapour and air.

3) Sink or cold reservoir: It is maintained at a very low temperature T₂. It absorbs heat energy, rejected by working substance.
Work done : The difference of heat absorbed from source and heat rejected to sink is equal to work done by the engine.
i.e.,W = Q₁ – Q₂.

Efficiency : The ratio of workdone (W) by the engine to the amount of heat absorbed (Q.,) by the engine is called efficiency.
i.e., η = \(\frac{W}{Q_1}=\frac{Q_1-Q_2}{Q_1}\) = 1 – \(\frac{Q_2}{Q_1}\)

Refrigerator : Refrigerator is a heat pump which is the reverse of a heat engine.

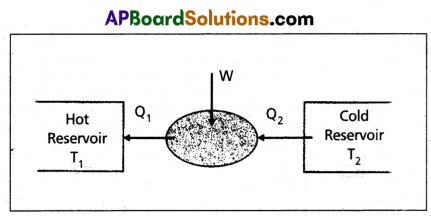
In refrigerator the working substance extracts (Q₂) an amount of heat from sink of lower temperature and a external work W is done on the working substance and finally amount of heat (Q₁) is transfered to source.

The coefficient of performance (α) of a refrigerator is given by
α = \(\frac{Q_2}{W}=\frac{Q_2}{Q_1-Q_2}\) (∵ heat released Q₁ = Q₂ + W)
For heat engine η can never exceed 1. For refregirator α can be greater than 1.
Therefore working of refrigerator is opposite to that of heat engine.