AP Inter 1st Year Physics Question Paper March 2017

Thoroughly analyzing AP Inter 1st Year Physics Model Papers and AP Inter 1st Year Physics Question Paper March 2017 helps students identify their strengths and weaknesses.

AP Inter 1st Year Physics Question Paper March 2017

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer all questions.
• Each question carries two marks.
• All are very short answer type questions.

Question 1.
What is the contribution of S. Chandra Sekhar to Physics ?
Answer:
While studying the constitution of the stars, he has proved that the maximum mass that a white dwarf can have is 1.4 times the solar mass. This mass is known as Chandrasekhar limit. If a star crosses this limit, it has to face a catostropic collapse.

Question 2.
How can systematic errors be minimized or eliminated ?
Answer:
Systematic errors can be minimised by improving experimental techniques, selecting better instruments and removing personal bias as far as possible. For a given set up, these errors may be estimated to a certain extent and the necessary corrections may be applied to the readings.

Question 3.
Two forces of magnitudes 3 units and 5 units act at 60° with each other. What is the magnitude of their resultant ?
Answer:
Let P = 3 units, Q = 5 units, θ = 60°
Resultant (R) = \(\sqrt{P^2+Q^2+2 P Q \cos \theta}\)
= \(\sqrt{3^2+5^2+2 \times 3 \times 5 \times \cos 60^{\circ}}\)
= \(\sqrt{9+25+30 \times \frac{1}{2}}\) = \(\sqrt{49}\) = 7 units.

Question 4.
A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12 ms^-1. If the mass of the ball is 0.15 kg., determine the impulse imparted to the ball. (Assume linear motion of the ball).
Answer:
u = 12 m/s, m = 0.15 kg
Impulse = Change in momentum = mu – (-mu)
= 2mu
= 2 × 0.15 × 12 = 3.6 NS

Question 5.
Why are drops and bubbles spherical ?
Answer:
The surface tension of a liquid tends to have minimum surface area. For a given volume, the surface area is minimum for a sphere. Hence rain drops are spherical shape.

Question 6.
Define average pressure. Mention its unit.
Answer:
Average pressure (P_av): Average power is defined as the normal force acting per unit area.
P_av = \(\frac{F}{A}\)
units N/m² (or) pascal
Dimensional formula → [ML^-1 T^-2]
Pressure is a scalar quantity.

Question 7.
Why gaps are left between rails on a railway track ?
Answer:
The length of the rails increases in summer due to high temperature. Therefore a gap is left to allow this expansion.

Question 8.
State Wein’s displacement law.
Answer:
The wavelength (λ_m) corresponding to maximum energy emitted by a black body is inversely proportional to its absolute temperature (T).
i.e., λ_m α \(\frac{1}{\mathrm{~T}}\)

Question 9.
Define mean free path.
Answer:
The average distance covered by a molecule between two •successive collisions is called the mean free path.

Question 10.
What is the expression between pressure and kinetic energy of a gas molecule ?
Answer:
By kinetic theory pressure, P = \(\frac{1}{3}\)mn\(\overline{\mathrm{V}}\)² and kinetic energy = \(\frac{1}{2}\)mn\(\overline{\mathrm{V}}\)² where m is the mass of the molecules, n is the number of moles per unit volume, v is the mean-square-speed.
∴ P = \(\frac{2}{3}\) (\(\frac{1}{2}\)mn\(\overline{\mathrm{V}}\)²) = \(\frac{2}{3}\) (kinetic energy)

Section – B (6 × 4 = 24)

Note :

• Answer any six questions.
• Each question carries four marks.
• All are Short Answer type Questions.

Question 11.
Two balls are projected from the same point in the directions 30° and 60° with respect to the horizontal. What is the ratio of their initial velocities if they (a) attain the same height ? (b) have the same range ?
Answer:
θ₁ = 30°, θ₂ = 60°

Question 12.
Show that the trajectory of an object thrown at a certain angle with the horizontal is a parabola.
Answer:

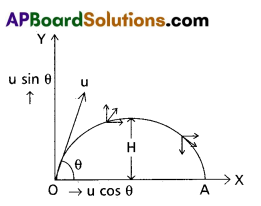
Consider a body is projected with an initial velocity (u) making an angle θ with the horizontal. The body does not experience acceleration in horizontal direction. The velocity of the projectile can be resolved in to (i) u cos θ, horizontal component (ii) u sin θ, vertical component. The horizontal component of velocity remains constant through out the motion. Only its vertical component changes due to acceleration due to gravity (g).
The distance travelled along OX in time t is given by
x = u cos θ × t
t = \(\frac{x}{u \cos \theta}\) → (1)
The distance travelled along oy in time t is given by
y = (u sin θ)t – \(\frac{1}{2}\) gt² → (2)
(∵ u = u sin θ)
substituting eq (1) in eq (2) a = – g
y = (u sin θ) \(\frac{x}{u \cos \theta}\) – \(\frac{1}{2}\) g (\(\frac{x^2}{u^2 \cos ^2 \theta}\)) s = y
y = x tan θ – (\(\frac{\mathrm{g}}{2 \mathrm{u}^2 \cos ^2 \theta}\)) x²
Let A tan θ and B = \(\frac{\mathrm{g}}{2 \mathrm{u}^2 \cos ^2 \theta}\)
Y = Ax – Bx² where A and B are constants.
This is the equation of parabola.
∴ The trajectory of a projectile is parabpla.

Question 13.
State Newton’s second law of motion. Hence, derive the equation of a motion F = ma from it.
Answer:
Newton’s Second of motion : “The rate of change of momentum of a body is directly proportional to the external force applied and takes place in the same direction”.

To show F = ma : Let a body of mass ‘m’ moving with a velocity V under the action of an external force F in the direction of velocity. Momentum ‘P of a body is the product of the mass and velocity V.
∴ P = mv …………. (1)
According to Newton’s second law of motion, we have
\(\frac{\mathrm{dp}}{\mathrm{dt}}\) α F, where F = external force
(or) F = K\(\frac{\mathrm{dp}}{\mathrm{dt}}\) ………. (2)
From equations (1) and (2) we have
F = K \(\frac{\mathrm{d}(\mathrm{mv})}{\mathrm{dt}}\) = K.m \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = Kma ………… (3)
Since the rate of change of velocity \(\frac{\mathrm{dv}}{\mathrm{dt}}\) is the acceleration ‘a’ of the body.
In SI system the unit of force is Newton and is defined as that force which when acting on a body of mass 1 kg produces in it an acceleration of 1 ms^-2.
i. e., from equation (3),
If F = 1, m = 1 and a = 1 we get K = 1
Hence F = \(\frac{\mathrm{dp}}{\mathrm{dt}}\) = ma
∴ F = ma

Question 14.
Distinguish between centre of mass and centre of gravity.
Answer:

Centre of mass	Centre of gravity
1. Point at which entire mass of the body is supposed to be concentrated, and the motion of the point represents motion of the body.	1. Fixed point through which the weight of the body act.
2. It refers mass of to body.	2. It refers to the weight acting on all particles of the body
3. In a uniform gravitational field centre of mass and centre of gravity coincide	3. In a non-uniform gravitational field, centre of gravity and centre of mass do not coincide.
4. Centre of mass of the body is defined to describe the nature of motion of a body as a whole.	4. Centre of gravity of body is defined to know the amount of stability of the body when supported.

Question 15.
Define vector product. Write the properties of a vector product.
Answer:
The cross product of two vectors is given by \(\vec{C}\) = \(\vec{A}\) × \(\vec{B}\) . The magnitude of the vector defined from cross product of two vectors is equal to product of magnitudes of the vectors and sine of angle between the vectors.

Direction of the vectors is given by right hand corkscrew rule and is perpendicular to the plane containing the vectors.

∴ | \(\vec{C}\) | = AB sin θ. and \(\vec{C}\) = AB sin θ n̂. Where, n̂ is the unit vector perpendicular to the plane containing the vectors \(\vec{A}\) and \(\vec{B}\)

Example :
1) Torque is cross product of position vector and Force.
i.e., \(\vec{T}\) = \(\vec{r}\) × \(\vec{F}\)

2) Angular momentum is cross product of position vector and momentum
i.e., \(\vec{L}\) = \(\vec{r}\) × \(\vec{P}\)

Properties :
1) Cross product does not obey commutative law. But its magnitude obey’s commutative law.
\(\vec{A}\) × \(\vec{B}\) ≠ \(\vec{B}\) × \(\vec{A}\) ⇒ (\(\vec{A}\) × \(\vec{B}\)) = – (\(\vec{B}\) × \(\vec{A}\)) , |(\(\vec{A}\) × \(\vec{B}\))| = |(\(\vec{B}\) × \(\vec{A}\))|

2) It obeys distributive law \(\vec{A}\) × (\(\vec{B}\) × \(\vec{C}\)) = \(\vec{A}\) × \(\vec{B}\) + \(\vec{A}\) × \(\vec{C}\)

3) The magnitude of cross product of two vectors which are parallel is zero.
Since θ = 0; | \(\vec{A}\) × \(\vec{B}\) | = AB sin 0° = 0

4) For perpendicular vectors, θ = 90°, | \(\vec{A}\) × \(\vec{B}\) | = AB sin 90° | n̂ | = AB

Question 16.
What is orbital velocity ? Obtain an expression for it.
Answer:
Orbital velocity (V₀) : The horizontal velocity required for an object to revolve around a planet in a circular orbit is called orbital velocity.

Expression for orbital velocity :
Consider a body (satellite) of mass m, revolves round the earth in a circular orbit. Let h be the height of the satellite from the surface of the earth. Then (R + h) is the radius of the orbit.
The Gravitational force of attraction of the earth on the body is given by F = \(\frac{G M m}{(R+h)^2}\) → (1)
Where M = Mass of the earth, R = Radius of the earth, G = universal gravitational constant.
If V₀ is the orbital velocity of the body.
The centripetal force on the body is given by F = \(\frac{m v_o{ }^2}{(R+h)}\) → (2)

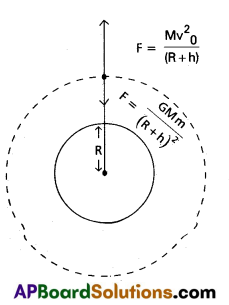
In order to make the body revolve in the same orbit, its centripetal force must be equal to the gravitational force From eq’s (1) and (2),

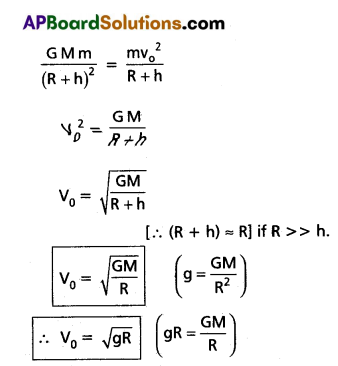
Question 17.
Describe the behaviour of a wire under gradually increasing load.
Answer:
When the load is increased in steps, a graph is drawn between stress on y-axis and corresponding strain on x-axis.

1. Proportionality limit : In the linear position OA, stress is proportional to strain, i.e. Hookes law is obeyed by the wire upto point A. The graph is a straight line. When ever the stretching force at A is removed, the wire regains its original length.
A is called proportionality limit.

2. Elastic limit : In the graph B is the elastic limit. Through the wire does not obey Hooke’s law at B. The wire regains its original length after removing the stretching force at B. Up to point B the wire is under elastic behaviour.

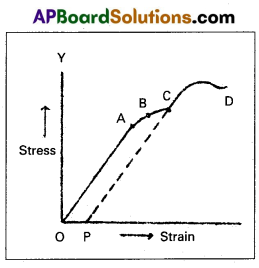
3. Permanent set (or) yield point : In the graph c is the yield point. If the stretching force at c is removed, the wire doesnot regain its original length and the length of the wire changes permanently. In this position the wire flows like a viscous liquid. After the point c, the wire is under plastic behavior, c is called permanent set (or) yield point.

4. Breaking point: When the stress increased, the wire becomes thinner and thinner. When the stress increases to a certain limit the wire breaks. The stress at which the wire breaks is called breaking stress and the point D is called breaking point.

5. Elastic fatigue : The state of temperary loss of elastic nature of a body due to continuous strain is called elastic fatigue. When a body is subjected to continuous strain with in the elastic limit, it appears to have lost elastic property temporarily to some extent and becomes weak.

Question 18.
In what way is the anomalous behaviour of water advantageous to aquatic animals ?
Answer:
In cold countries, as atmospheric temperature decreases, the upper layers of the lakes, rivers etc., cool, contract and sink to the bottom (fig). This goes on until the whole of the water reaches the temperature of 4°C. When the top layers cool further temperature falls below 4°C, it expands and becomes lighter. It does not sink downwards and remains at the top. With further cooling the top layer gradually form ice at the top (fig). Ice and water are bad conductors of heat. So the lower layers are protected against freezing by the layers of ice and cold water at 1°C, 2°C and 3°C. This results in water remaining at the bottom at 4°C. So that aquatic animals survive in those layers of water.

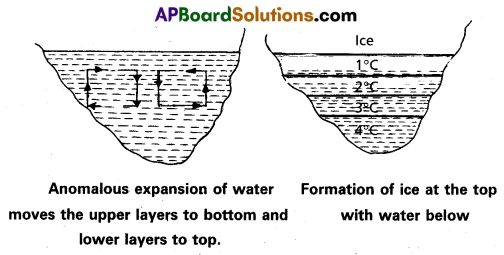
Section – C (2 × 8 = 16)

Note :

• Answer any two questions.
• Each question carries eight marks.
• All are Long Answer Type Questions.

Question 19.
Develop the notions of work and kinetic energy and show that it leads to work energy theorem.
Answer:
Statement : The change in kinetic energy of a particle is equal to the workdone on it by the net force, i.e., k_f – k_i = W

Proof : Consider a particle of mass ‘m’ is moving with initial speed ‘u’ to final speed ‘v’. Let ‘a’ be its constant acceleration and S be its distance traversed. The kinematic relation is given by
v² – u² = 2as ………… (1)
Multiplying both sides by \(\frac{\mathrm{m}}{2}\), we have
\(\frac{1}{2}\)mv² – \(\frac{1}{2}\)mu² = mas = FS …………. (2)
Where the last step follows from Newton’s second law.
We can generalise Equation (1) to three dimensions by employing vectors
v² – u² = 2 \(\overrightarrow{\mathrm{a}}\) . \(\overrightarrow{\mathrm{d}}\)
Once again multiplying both sides by \(\frac{\mathrm{m}}{2}\), we obtain
\(\frac{1}{2}\)mv² – \(\frac{1}{2}\)mu² = m\(\overrightarrow{\mathrm{a}}\) . \(\overrightarrow{\mathrm{d}}\) = \(\overrightarrow{\mathrm{F}}\) . \(\overrightarrow{\mathrm{d}}\) ………. (3)
The above equation provides a motivation for the definitions of work and kinetec energy.
In equation (3), \(\frac{1}{2}\)mv² – \(\frac{1}{2}\)mu² = k_f – k_i
Where k_i, k_f are initial and final kinetic energies and \(\overrightarrow{\mathrm{F}}\) . \(\overrightarrow{\mathrm{d}}\) = W, where W refers workdone by a force on the body over a certain displacement.
k_f – k_i ………… (4)
Equation (4) is also a special case of the work-energy (WE) theorem.

Question 20.
Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period.
What is seconds pendulum, which ticks seconds ?
Answer:
i) Consider simple pendulum, a small bob of mass m tied to an inextensible mass less string of length L and other end of the string is fixed from a rigid support.

ii) Once the bob is slightly displaced and released, it begins to oscillate about mean position.

iii) Let θ be the angular displacement and T be the tension in the string.

iv) The forces acting on the bob are (a) tension T alang the string (b) weight mg acts vertically downwards.

v) The force mg can be resolved into two components (1) mg cos θ along the PA and (2) mg sin θ acts along PB.

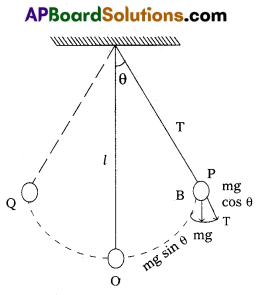
vi) From figure at point P,
T = mg
cos θ …………. (1)

vii) The force mg sin θ will provide the restoring torque, which tends to bring the bob back to its mean position O.

viii) The restoring torque is given by
τ = Restoring force × ⊥^lar distance
τ = -mg sin θ × L ………. (2)
Here negative sign shows that the torque acts to reduce θ.
Then sin θ is replaced by θ i.e., sin θ ≈ θ
τ = -mg L θ …………. (3) (∵ sin θ = θ – \(\frac{\theta^3}{3 !}\) + \(\frac{\theta^5}{5 !}\) …… )

ix) From equation (3), we note that τ ∝ θ and This τ will bring the bob back towards its equilibrium position.
So, if the bob is left free, it will execute angular simple harmonic motion.
Comparing equation (3), with the equation τ = -kθ, we have
Spring factor, k = mgL.

x) Here inertia factor = Moment of inertia of the bob about the point of suspension = mL²

xi) In S.H.M, Time period (T) = \(2 \pi \sqrt{\frac{\text { Inertia factor }}{\text { Spring factor }}}\)
T = \(2 \pi \sqrt{\frac{\mathrm{mL}^2}{\mathrm{mgL}}}\)
T = \(2 \pi \sqrt{\frac{L}{g}}\) ………… (4)

Seconds pendulum : A pendulum whose time period is 2 seconds is called seconds pendulum.
T = 2 seconds.
Problem :
In seconds pendulum T = 2 sec
T = \(2 \pi \sqrt{\frac{l}{g}}\)
l = \(\frac{T^2 g}{4 \pi^2}\) = \(\frac{(2)^2 \times 9.8}{4 \times(3.14)^2}\) ≈ 100 cm = 1 m

Question 21.
Explain reversible and irreversible process. Describe the working of Carnot Engine. Obtain an expression for the efficiency.
Answer:
Reversible process : A process that can be retraced back in the opposite direction in such away that the system passes through the same states as in the direct process, and finally the system and the surroundings return in their original states, is called a reversible process. A reversible process is only a purely idealised process.

Examples :
i) Slow isothermal and slow adiabatic changes
ii) Peltier effect and seeback effect.
iii) Fusion of ice and vaporisation of water.

Irreversible process : “A process that cannot be retraced back in the opposite direction” is called as irreversible process.
In this process the system does not pass through the same intermediate states as in the reversible process.
All natural processes such as conduction, radiation, radioactivity etc, are irreversible.

Example :
i) Work done against friction.
ii) Heat produced in conductors by passing a current through it. (Joule heating)
iii) Diffusion of gases.

Carnot Engine : A reversible heat engine operating between two temperatures is called a carnot engine. The cycle operating it is known as carnot’s cycle. In this cycle the working substance(say an ideal gas) is taken through a cycle by means of two isothermals and two adiabatics. The four operations are shown in P – V (Indicator) diagram.

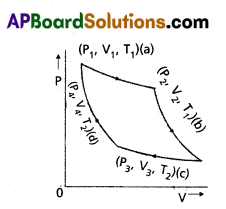
Step 1 → 2 : Isothermal expansion of the gas taking its state from (P₁, V₁, T₁) to (P₂, V₂, T). It is shown in curve (a).
The heat absorbed by the gas (Q₁) from the reservoir at temperature T₁ equals the workdone by the gas. i.e.
W_{1 → 2} = Q₁ = μRT₁ log_e \(\frac{V_2}{V_1}\) ……. (1)

Step 2 → 3 : Adiabatic expansion of the gas from (P₂, V₂, T₁) to
(P₃, V₃, T₂). It is shown in curve (b). The work done by the gas is given by
W_{2 → 3} = \(\frac{\mu R\left(T_1-T_2\right)}{(r-1)}\)

Step 3 → 4 : Isothermal compression of the gas from (P₃, V₃, T₂) to (P₄, V₄, T₂). It is shown in curve (c).
Heat released (Q₂) by the gas to the reservoir at temperature T₂ equals the work done on the goes.
i.e., W_{3 → 4} = μRT₂ log_e\(\frac{V_4}{V_3}\) = – μRT₂ log_e\(\frac{V_3}{V_4}\)