AP Inter 1st Year Physics Important Questions Chapter 9 గురుత్వాకర్షణ

Students get through AP Inter 1st Year Physics Important Questions 9th Lesson గురుత్వాకర్షణ which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 9th Lesson గురుత్వాకర్షణ

Very Short Answer Questions (అతిస్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
విశ్వ గురుత్వస్థిరాంకం ప్రమాణాలను, మితులను తెలపండి? [Imp.Q]
జవాబు:
విశ్వగురుత్వ స్థిరాంకం యొక్క S.I. ప్రమాణం : N m²kg^-2
మితిఫార్ములా : M^-1L³T^-2

ప్రశ్న 2.
న్యూటను విశ్వగురుత్వాకర్షణ నియమమును సదిశా రూపములో వ్రాయండి. [Imp.Q]
జవాబు:
న్యూటను విశ్వగురుత్వాకర్షణ నియమమును సదిశా రూపములో ఈ క్రింది విధంగా వ్రాయవచ్చును.

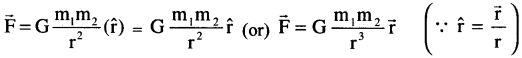
\(\overrightarrow{F}\) = m₂ ద్రవ్యరాశి గల వస్తువు m, ద్రవ్యరాశి గల వస్తువు పై ప్రయోగించిన బలం.
r = m₁,m₂ ద్రవ్యరాశుల మధ్యగల దూరం \(\hat{r}\) = m₂, m₁ వస్తు కేంద్రములను కలుపుచూ గీయు సరళరేఖ దిశలో యూనిట్ సదిశ. దీని దిశ m₂ నుండి m₁ వైపునకు ఉండును.
m₁పై m₂ ప్రయోగించు బలం \(\overrightarrow{F}\) దిశకు \(\hat{r}\) దిశ వ్యతిరేకం కనుక ఋణసంజ్ఞను ఉపయోగించవలయును.

ప్రశ్న 3.
చంద్రునిపై భూమి యొక్క గురుత్వాకర్షణ బలం F అయితే, భూమిపై చంద్రుని గురుత్వాకర్షణ బలం ఎంత? ఈ బలాలు చర్య-ప్రతిచర్య జంటను ఏర్పరుస్తాయా?
జవాబు:
భూమి పై చంద్రుని గురుత్వాకర్షణ బలం కూడా F కు సమానం. ఈ రెండు బలములు చర్య – ప్రతిచర్య అగును.

ప్రశ్న 4.
భూమి ద్రవ్యరాశిని స్థిరంగా ఉంచుతూనే, భూమి వ్యాసార్థం 2% తగ్గిస్తే, దాని ఉపరితలం వద్ద గురుత్వ త్వరణం విలువ (g) లో వచ్చే మార్పు ఎంత ఉంటుంది?
జవాబు:
వ్యాసార్థములోని తగ్గుదల శాతం \(\frac{dR}{R}\) =-2% భూ ఉపరితలము పై g = \(\frac{GM}{R^2}\)
ఇరువైపుల సంవర్గమానములు తీసుకొనగా log g = log GM R^-2 = log GM + logR^-2 = logGM – 2log R
ఇరువైపుల అవకలనము చేయగా \(\frac{dg}{g}=\frac{-2dR}{R}\) = -2 × (−2%) = 4%
∴ కావున భూ ఉపరితలము పై g విలువ 4% పెరుగును.

ప్రశ్న 5.
మనం ఒక గ్రహం నుంచి మరొక గ్రహానికి మారుతూ ఉంటే వస్తువు (a) ద్రవ్యరాశి (b) భారం ఎలా మారుతుంటాయి? [Imp.Q]
జవాబు:
a) మన శరీర ద్రవ్యరాశి మారదు.
b) g విలువలో మార్పు వలన ఒక్కొక్క గ్రహానికి వస్తువు యొక్క భారం మారుతుంది.
మరియు g = \(\frac{GM}{R^2}\) ⇒ w = m\(\frac{GM}{R^2}\) ⇒ w \(\frac{M}{R^2}\)
కావున వస్తువు భారం, గ్రహము ద్రవ్యరాశికి అనులోమానుపాతంలోను, గ్రహము వ్యాసార్థము యొక్క వర్గమునకు విలోమానుపాతములో ఉండును. అందువలన గ్రహము నుండి గ్రహమునకు వస్తు భారము మారుచుండును.

ప్రశ్న 6.
ఒక లఘులోలకం పొడవును స్థిరంగా ఉంచినప్పుడు, అన్ని గ్రహాల మీద దాని డోలనావర్తన కాలం సమానంగా ఉంటుందా? కారణంతో సహా మీ సమాధానాన్ని సమర్థించండి.
జవాబు:
లఘులోలకం ఆవర్తనకాలం T = 2π\(\sqrt{\frac{l}{g}}\) ;పొడవు ‘l’ ను స్థిరంగా ఉంచితే T ∝ \(\frac{l}{\sqrt{g}}\)
వేరు వేరు గ్రహాలపై g విలువ వేరువేరుగా ఉంటుంది. కాబట్టి లోలక ఆవర్తన కాలం మారుతుంది.

ప్రశ్న 7.
భూఉపరితలం నుండి ‘d’ లోతు ఉన్న బిందువు వద్ద గురుత్వ త్వరణానికి సమీకరణాన్ని తెలపండి. భూకేంద్రం వద్ద g విలువ ఎంత?
జవాబు:
భూ ఉపరితలంపై గురుత్వ త్వరణం విలువ g మరియు భూమి వ్యాసార్థం R అయితే భూ ఉపరితలం నుండి ‘d’
లోతు వద్ద గురుత్వత్వరణం g_d = g(1 – \(\frac{d}{R}\))
భూమి కేంద్రం వద్ద గురుత్వ త్వరణం విలువ సున్న.

ప్రశ్న 8.
g విలువ భూమధ్య రేఖ వద్ద కనిష్టంగా, ధ్రువాల వద్ద గరిష్టంగా ఉండే విధంగా చేసే అంశాలేమిటో తెలపండి.
జవాబు:
1. భూమి ఆకారం :
భూమి సంపూర్ణ గోళాకృతిలో లేదు. భూమధ్యరేఖ వద్ద ఉబ్బెత్తుగా, ధ్రువాల వద్ద నొక్కుకు పోయినట్లుగా ఉండును. దీని వలన భూమధ్యరేఖ వద్ద భూవ్యాసార్థం ఎక్కువగాను, ధ్రువాల వద్ద తక్కువగా ఉండును.
g = \(\frac{GM}{R^2}\) “కనుక భూమధ్యరేఖ వద్ద g విలువ కనిష్టముగాను, ధ్రువాల వద్ద గరిష్టముగాను ఉండును.

2. భూభ్రమణం :
భూభ్రమణం వలన అక్షాంశము 9 గల ప్రదేశము వద్ద గురుత్వత్వరణం g_θ = g – Rω² cos² θ
భూమధ్యరేఖ వద్ద θ = 0 అందువలన g_θ = g – Rω²
ధ్రువాల వద్ద θ = 90° అందువలన g_θ = g – 0 = g
అనగా భూభ్రమణం వలన భూమధ్యరేఖ వద్ద g విలువ తగ్గును. ధ్రువాల వద్ద తగ్గదు.

ప్రశ్న 9.
“హైడ్రోజన్ సూర్యుని చుట్టూ పుష్కలంగా ఉంది. కాని భూమి చుట్టూ అంత పుష్కలంగా లేదు”. వివరించండి.
జవాబు:
సూర్యునిపై పలాయన వేగం భూమిపైన పలాయన వేగం కంటే చాలా ఎక్కువ. అందువలన హైడ్రోజన్ సూర్యుని ఆవరణ నుండి పలాయనం చెందదు.

ప్రశ్న 10.
ఒక భూస్థావర ఉపగ్రహం పరిభ్రమణావర్తన కాలం ఎంత? అది పశ్చిమం నుంచి తూర్పుకి లేదా తూర్పు నుంచి పశ్చిమానికి తిరుగుతుందా?
జవాబు:
కక్ష్యావర్తన కాలం 24 గంటలు. ఇది పడమర నుండి తూర్పునకు తిరుగుతుంది.

ప్రశ్న 11.
ధ్రువీయ ఉపగ్రహాలు అంటే ఏమిటి?
జవాబు:
భూమి ఉపరితలము నుండి తక్కువ ఎత్తులలో (సుమారుగా 500 నుండి 800km ఎత్తు) భూమి ఉత్తర, దక్షిణ ధ్రువముల మీదుగా ప్రయాణించు ఉపగ్రహములను ధ్రువీయఉపగ్రహాలు అని అంటారు. దీని కక్ష్యావర్తన కాలం సుమారుగా 100 నిమిషాలు. ఇవి భూమికి దగ్గరగా తిరుగుట వలన భూమిపై ప్రదేశములను చాలా స్పష్టముగా చిత్రీకరించును.

Short Answer Questions (స్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
కెప్లర్ గ్రహ గమన నియమములను వ్రాయండి.? [TS 17, 20] [Imp.Q]
జవాబు:
కెప్లర్ గ్రహ నియమములు మూడు. అవి

1. కక్ష్యా నియమం :
సూర్యుని ఒక నాభిగా చేసుకొని సూర్యుని చుట్టూ వేర్వేరు గ్రహములు వేర్వేరు దీర్ఘవృత్తాకార కక్ష్యలలో పరిభ్రమించు చుండును.

2. విస్తీర్ణ నియమం :
సూర్యుడుని, గ్రహాన్ని కలిపే సదిశ త్రిజ్య (లేక సరళ రేఖ) సమాన కాల వ్యవధులలో సమాన విస్తీర్ణములను (వైశాల్యములను ) విరజిమ్మును.

3. పరిభ్రమణ కాల నియమం :
సూర్యుని చుట్టూ తిరిగే ఒక గ్రహము పరిభ్రమణ కాల వర్గము(T²), ఆ గ్రహము సూర్యుని చుట్టూ తిరిగే దీర్ఘవృత్తాకార కక్ష్య అర్థ గురు అక్ష ఘనమునకు (a³) అనులోమాను పాతంలో ఉండును.

ప్రశ్న 2.
ఒక గ్రహం ఉపరితలంపై గురుత్వ త్వరణం విలువ (g), విశ్వగురుత్వ స్థిరాంకం (G) ల మధ్య సంబంధాన్ని రాబట్టండి. [AP 19][Imp.Q]
జవాబు:
‘m’ ద్రవ్యరాశి గల వస్తువు M ద్రవ్యరాశి, R వ్యాసార్ధం గల ఒక గ్రహంపై ఉందనుకుందాం. న్యూటన్ రెండవ గమన నియమం ప్రకారం వస్తువుపై పనిచేసేబలం F = mg ….(1)

ప్రశ్న 3.
సమాన విలువలు కలిగిన ఎత్తు ‘h’ మరియు లోతు ‘d’ లకు గురుత్వ త్వరణం విలువ ఏవిధంగా మారుతుంది? [Imp.Q]
జవాబు:

ప్రశ్న 4.
కక్ష్యావేగం అంటే ఏమిటి? దాని సమీకరణం రాబట్టండి. [AP 17, 18] [IPE’ 10, 10, 14, 14]
జవాబు:
కక్ష్యావేగం :
ఒక ఉపగ్రహం, ఒక గ్రహం చుట్టూ ఒక నిర్ణీత కక్ష్యలో పరిభ్రమించుచున్నపుడు, దానికి ఉండే వేగాన్ని కక్ష్యావేగం (Vo) అని అంటారు.

కక్ష్యావేగమునకు సమీకరణం రాబట్టుట :
భూమి ద్రవ్యరాశి M మరియు భూమి వ్యాసార్థం R అనుకొనుము. భూమి ఉపరితలం నుండి ‘h’ ఎత్తు గల కక్ష్యలో m ద్రవ్యరాశి గల ఒక ఉపగ్రహము Vo వేగంతో భూమి చుట్టూ పరిభ్రమించుచున్నదనుకొనుము. Vo ను కక్ష్యా వేగం అని అంటారు. ఉపగ్రహం భూమి చుట్టూ తిరుగుటకు కావలసిన అభికేంద్ర బలమును, భూమికి ఉపగ్రహమునకు మధ్యగల గురుత్వాకర్షణ బలము సమకూర్చును.

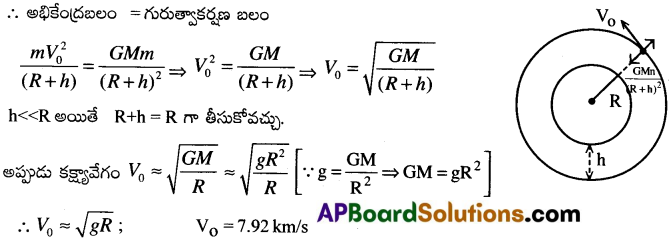
ప్రశ్న 5.
పలాయన వేగం అంటే ఏమిటి? దాని సమీకరణం రాబట్టండి. [AP 15,16,17,18,19] [TS 16,17,19,22]
జవాబు:
పలాయన వేగం :
ఒక గ్రహం గురుత్వాకర్షణ ప్రభావం నుంచి తప్పించుకుని పోవడానికి ఒక వస్తువునకు ఉండవలసిన కనీస వేగాన్ని ఆ గ్రహము మీద పలాయన వేగం అని అంటారు.

పలాయన వేగమునకు సమీకరణం రాబట్టుట:
భూమి ద్రవ్యరాశి M, భూమి వ్యాసార్థం R అనుకొనుము. భూమి ఉపరితులము పై ‘m’ ద్రవ్యరాశి గల వస్తువునకు ఉండు స్థితిశక్తి = \(\frac{-GMm}{R}\)
భూమిపై పలాయన వేగం V_e. అనుకొనుము. ఇపుడు ‘m’ ద్రవ్యరాశి గల వస్తువును V_e వేగంతో పైకి విసిరితిమి అని అనుకొనుము. అపుడు వస్తువునకు గల గతి శక్తి = \(\frac{1}{2}\)mV_e²

∴ వస్తువు భూమి పై ఉన్నపుడు మొత్తం శక్తి = స్థితి శక్తి + గతి శక్తి ⇒ మొత్తం శక్తి = –\(\frac{GMm}{R}\) + \(\frac{1}{2}\)mV_e² ……. (1)
భూమిపై పలాయన వేగము అనగా భూమి గురుత్వాకర్షణ ప్రభావం నుండి తప్పించుకుని పోవుటకు వస్తువునకు కావలసిన కనీస వేగం కనుక భూమి గురుత్వాకర్షణ పరిధిని దాటిన తరువాత ఆ వస్తువు వేగం శూన్యము అని అనుకొనుము. అనగా దాని గతి శక్తి సున్న. వస్తువుపై భూమి గురుత్వాకర్షణ లేదు. కనుక దాని స్థితిశక్తి కూడా సున్న. అనగా మొత్తం శక్తి సున్నా.
∴ శక్తి నిత్యత్వ నియమం ప్రకారం, (1) నుండి

ప్రశ్న 6.
భూస్థావర ఉపగ్రహము అనగా ఏమి? దాని ఉపయోగాలను వ్రాయండి. [AP 22][AP, TS 15,16,18,20,22]
జవాబు:
భూస్థావర ఉపగ్రహం :
ఒక కృత్రిమ ఉపగ్రహం యొక్క కక్ష్యావర్తన కాలం భూమి భ్రమణావర్తన కాలానికి సమాన మైతే అలాంటి ఉపగ్రహాన్ని భూస్థావర ఉపగ్రహం అని అంటారు.

ఉపయోగాలు:

1. రేడియో, టెలివిజన్ కార్యక్రమములను ప్రసారం చేయడానికి.
2. వాతావరణంలో వచ్చే మార్పులను ముందే పసిగట్టడానికి.
3. సూర్యుని నుండి, బాహ్యవిశ్వము నుండి వచ్చుచున్న వికిరణములను పరిశీలించుట కొరకు
4. భూమి పై వాతావరణమును పరిశీలించుట కొరకు ఉపయోగిస్తారు.

ప్రశ్న 7.
సరాసరి సముద్ర మట్టం నుండి రెండు ప్రదేశాలు ఒకే ఎత్తులో ఉన్నాయనుకొందాం. ఒకటి పర్వతం మీద ఉంది. మరొకటి గాలిలో ఉంది. ఎక్కడ g విలువ ఎక్కువగా ఉండును? మీ సమాధానికి కారణం తెలపండి.
జవాబు:
పర్వతముపైన గల ప్రదేశము వద్ద g విలువ ఎక్కువగా ఉండును. కారణం g = \(\frac{GM}{(R+h)^2}\)
రెండు ప్రదేశములు ఒకే ఎత్తు (h) వద్ద ఉన్నవి కనుక g ∝ M
పర్వతము వద్ద ఎక్కువ ద్రవ్యరాశి కేంద్రీకృతమవుట వలన అక్కడ g విలువ అధికము.

ప్రశ్న 8.
ఒక వస్తువు భారం భూమధ్యరేఖ వద్ద కంటె ధ్రువాల వద్ద ఎక్కువగా ఉంటుంది. ఒకే బరువుకు ఈ రెండు ప్రదేశాల్లో ఎక్కడ ఎక్కువ చక్కెర వస్తుంది? మీ సమాధానానికి కారణం తెలపండి.
జవాబు:
m ద్రవ్యరాశి గల వస్తువు భారము W = mg
g విలువ భూమధ్యరేఖ వద్ద కంటే ధ్రువాల వద్ద ఎక్కువ. అందువలన ఒక వస్తువు భారము ధ్రువాల వద్ద ఎక్కువగా ఉండును. (ద్రవ్యరాశి స్థిరముగా ఉన్నది కనుక)

కాని భారం, W స్థిరముగా ఉన్నపుడు అనగా mg స్థిరముగా ఉన్నపుడు m ∝ \(\frac{1}{g}\)
ధ్రువాల వద్ద g విలువ ఎక్కువ కనుక m విలువ తక్కువగా ఉండును. భూమధ్యరేఖ వద్ద g విలువ తక్కువ కనుక m విలువ ఎక్కువగా ఉండును. కాబట్టి ఒకే భారమునకు భూమధ్యరేఖ వద్ద ఎక్కువ పంచదార వచ్చును.

ప్రశ్న 9.
భూమి చుట్టూ తిరుగుచున్న ఒక కృత్రిమ ఉపగ్రహంలోని ఒక చీల వదులై దాని నుంచి వేరైతే అది భూమి వైపు క్రిందకు పడుతుందా? లేదా భూమి చుట్టూ తిరుగుతుందా? మీ సమాధానానికి కారణం తెలపండి.
జవాబు:
చీల(నట్) భూమి చుట్టూ పరిభ్రమించుచుండును.

కారణం :
మొదట నట్ ఉపగ్రహములో ఉన్నది కనుక ఉపగ్రహమునకు ఉన్న కక్ష్యావేగముతో అది భూమి చుట్టూ తిరుగుచుండును. ఉపగ్రహం నుండి విడి పడిన తరువాత కూడ నట్ పై పనిచేయు బలములలో మార్పు ఉండదు. అందువలన చలన జడత్వముతో అది భూమి చుట్టూ తిరుగుచుండును.

ప్రశ్న 10.
ఒక వస్తువును 11.2 కి.మీ సె^-1 వేగంతో లేదా అంతకంటే ఎక్కువ వేగంతో ప్రక్షిప్తం చేసినప్పుడు అది తిరిగి భూమికి చేరుకోలేదు. కారణాలతో వివరించండి.
జవాబు:
భూమి పై ఏ వస్తువుకైనా పలాయన వేగం 11.2 కి. మీసె^-1 కావున ఏదైనా వస్తువును ఆ వేగంతో లేక అంతకన్న ఎక్కువ వేగంతో విసిరినపుడు అది భూమి గురుత్వాకర్షణ పరిధి దాటి వెళ్ళును కనుక మరల భూమిపై పడదు.

Long Answer Questions (దీర్ఘ సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
గురుత్వ స్థితిజ శక్తిని నిర్వచించండి. m1, m2 ద్రవ్యరాశులు ఉన్న రెండు కణాలకు సంబంధించిన గురుత్వ స్థితిజశక్తికి సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
గురుత్వ స్థితిజ శక్తి :
గురుత్వాకర్షణ బలమునకు వ్యతిరేకంగా అనంత దూరము నుండి ఒక వస్తువును ఒక బిందువు వద్దకు తీసుకొని వచ్చుటకు చేసిన పనిని ఆ బిందువు వద్ద ఆ వస్తువునకు గల గురుత్వ స్థితిజ శక్తి అని అంటారు.

రెండు కణాల వ్యవస్థ యొక్క గురుత్వ స్థితిజ శక్తికి సమీకరణం :
m₁ ద్రవ్యరాశి గల వస్తువు యొక్క గురుత్వక్షేత్రములో దాని నుండి r దూరంలో గల బిందువు వద్దకు m₂ ద్రవ్యరాశి గల వస్తువును అనంత దూరము నుండి తీసుకొని వచ్చుటకు చేయవలసిన పనిని కనుక్కొందాము.

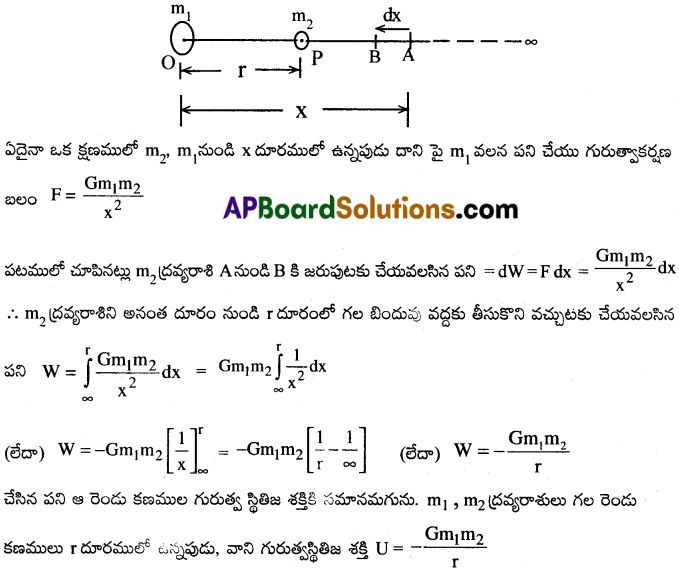
ప్రశ్న 2.
గురుత్వ త్వరణం (a) భూమి ఉపరితలంపైన (b) భూమి ఉపరితలం లోపల ఎలా మారుతుందో తెలిపే సమీకరణాలను ఉత్పాదించండి.
జవాబు:
(a) h ఎత్తులో గురుత్వత్వరణంలో (g)మార్పు :
భూమి ఉపరితలంపై ‘m’ ద్రవ్యరాశి గల వస్తువును పరిగణిద్దాం.

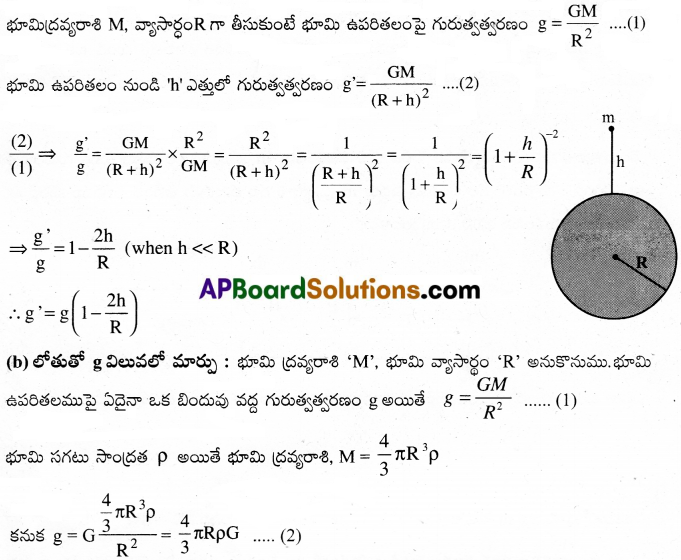
భూమి లోపల భూమి ఉపరితలం నుండి ‘d’ లోతు వద్ద గల ఒక బిందువును ఊహించుము. భూమి కేంద్రము నుండి ఆ బిందువు దూరము (R-d) అగును. ‘O’ కేంద్రముగా (R-d) వ్యాసార్థముతో ఒక గోళమును ఊహించిన, ఆ గోళము లోని భూద్రవ్యరాశి మాత్రమే వస్తువును భూమి కేంద్రమువైపు ఆకర్షించును. ఆ ద్రవ్యరాశి m అనుకొనుము. ఆ లోతు వద్ద గురుత్వ త్వరణం విలువ g_d అనుకుంటే

లోతుకు వెళ్ళుచున్న కొలది గురుత్వ త్వరణం మారు విధానమును పై సమీకరణం సూచించును.

ప్రశ్న 3.
న్యూటను విశ్వగురుత్వాకర్షణ నియమాన్ని పేర్కొనండి. కావెండిష్ పద్ధతి ద్వారా విశ్వగురుత్వ స్థిరాంకం విలువను ఎలా కనుక్కోంటారో వివరించండి.
జవాబు:
న్యూటన్ విశ్వగురుత్వాకర్షణ నియమం :
విశ్వంలోని ప్రతికణం మరొక కణాన్ని ఆకర్షిస్తుంది. ఈ ఆకర్షణ బలం ఆ’ రెండు కణాల ద్రవ్యరాశుల లబ్ధానికి అనులోమానుపాతంలోను, వాటి మధ్య దూర వర్గానికి విలోమానుపాతంలోను ఉంటుంది. ఈ బలం ఆ రెండు కణాల్ని కలిపే సరళరేఖ వెంబడి పనిచేస్తుంది.
రెండు కణాల ద్రవ్యరాశులు m, m, వాటి మధ్య దూరం అయితే గురుత్వాకర్షణబలం పరిమాణం F = \(\frac{Gm_1m_2}{r^2}\)
ఇక్కడ G ఒక స్థిరాంకం, దీనిని విశ్వగురుత్వాకర్షణ స్థిరాంకం అంటారు.
దీని విలువ G = 6.67 × 10^-11 N m²kg^-2
G యొక్క S.I ప్రమాణం : N m²kg^-2

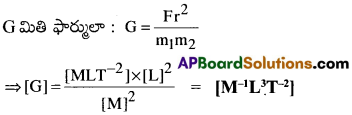
కావెన్హీష్ పద్ధతిలోG ను కనుగొనుట:

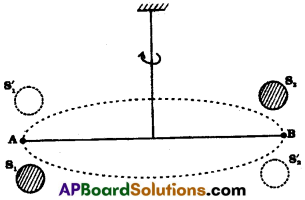
ఒక ధృడమైన ఆధారము నుండి AB అను ఒక కడ్డి ఒక తీగతో వ్రేలాడ దీయబడి ఉండును. ఈ కడ్డి చివర చిన్నవైన రెండు సీసపు గోళములు అతికించబడి ఉండును. పెద్దవైన రెండు సీసపు గోళములను ఈ రెండు చిన్నని సీసపు గోళముల వద్ద పటములో చూపినట్లు వ్యతిరేక దిశలో ఉంచినపుడు అవి చిన్న గోళములను సమానమైన ఆకర్షణ బలములను వ్యతిరేక దిశలో ప్రయోగించును. ఈ రెండు బలములు కలిసి బలయుగ్మముగా ఏర్పడి AB కడ్డీని భ్రమణము చెందించును. దీని వలన తీగ పురిపెట్టబడుతుంది. కాబట్టి తీగలో పునఃస్థాపక టార్క్ ఉద్భవిస్తుంది. పై రెండు టార్క్ విలువలు సమాన మైనపుడు తీగ నిశ్చల స్థితిని పొందుతుంది. తీగ θ కోణం చేసిన తరువాత నిశ్చల స్థితిని పొందినది అని అనుకొనుము. తీగను ప్రమాణ పురిపెట్టటానికి అవసరమైన బలయుగ్మ భ్రామకం τ అయితే పునఃస్థాపక టార్క్ = τθ పెద్ద సీసపు గోళం ద్రవ్యరాశి M చిన్న సీసపు గోళం ద్రవ్యరాశి m అనుకుందాం. పెద్ద సీసపు గోళకేంద్రానికి, దానికి దగ్గరగా యున్న చిన్న సీసపు గోళ కేంద్రానికి మధ్యదూరం d అయితే వాని మధ్యగల గురుత్వాకర్షణ బలం,

θ ను ప్రయోగము ద్వారా తెలిసికొని G విలువను కనుగొనవచ్చు.
ప్రస్తుతము ఉపయోగించుచున్న G విలువ = 6.67 × 10^-11 N m²kg^-2

Solved Problems (సాధించిన సమస్యలు)

ప్రశ్న 1.
భుజము పొడవు l గా ఉన్న ఒక చతురస్రం యొక్క ప్రతీ శీర్షం వద్ద ఒక్కో కణాన్ని ఉంచితే, ఆ నాలుగు కణాల వ్యవస్థ మొత్తం స్థితిజశక్తిని కనుక్కోండి. ఆ చతురస్ర కేంద్రం వద్ద పొటెన్షియల్ను కూడా గణించండి.
సాధన:
భుజము పొడవు l గల చతురస్రము యొక్క ప్రతీ శీర్షం వద్ద m ద్రవ్యరాశి గల కణాలు కలవు.
పటము నుండి l దూరంలో నాలుగు ద్రవ్యరాశుల జతలు, √2l దూరంలో కర్ణాల పరంగా రెండు ద్రవ్యరాశుల

ప్రశ్న 2.
ఈ క్రింది దత్తాంశముతో భూమి ద్రవ్యరాశి ని కనుక్కోండి.
g = 9.81 ms^-2, R_E = 6.37 × 10⁶ m, G = 6.67 × 10^-11 Nm²kg^-2
సాధన:

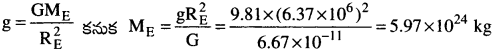
ప్రశ్న 3.
భూమి చుట్టూ 2R_E వ్యాసార్థము ఉన్న వృత్తాకార కక్ష్యలో 400 కి.గ్రా ద్రవ్యరాశి గల ఉపగ్రహము తిరుగుచున్నది. దానిని 4R_E వ్యాసార్థము గల వృత్తాకార కక్ష్యలోనికి పంపించుటకు కావలసిన శక్తి ఎంత? దాని స్థితిశక్తి, గతి శక్తులలో మార్పులు ఎంత?
సాధన:
భూ ఉపరితలము నుండి h ఎత్తులో భ్రమణము చేయుచున్న m ద్రవ్యరాశి గల ఉపగ్రహము మొత్తము శక్తి

ఎత్తునకు వెళ్ళుచున్న కొలది ఉపగ్రహము కక్ష్యావేగము తగ్గుచుండును. కావున గతిశక్తి తగ్గును. గతిశక్తిలోని తగ్గుదల -∆E, = −3.13 × 10⁹ J.
స్థితి శక్తి పెరుగును. స్థితిశక్తి లోని పెరుగుదల 2 × ∆E,= 6.26 × 10⁹ J.

Exercise Problems

ప్రశ్న 1.
1 కి.గ్రా ద్రవ్యరాశి గల రెండు గోళాకార బంతులు 1 సెం.మీ దూరములో ఉన్నవి. వాని మధ్యగల గురుత్వాకర్షణ బలం ఎంత?
సాధన:
ఇక్కడ m₁ = m₂ = 1 కి.గ్రా, r = 1 సెం.మీ = 10^-2 మీ. Also, G = 6.67 × 10^-11 Nm²kg^-2

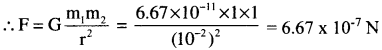
ప్రశ్న 2.
ఒక బంతి ద్రవ్యరాశి రెండవ బంతి ద్రవ్యరాశికి 4 రెట్లు . వీని మధ్య దూరం 10 సెం.మీ ఉన్నపుడు వీని మధ్యగల గురుత్వాకర్షణ బలం 6.67 × 10^-7 N అయిన వాని ద్రవ్యరాశులను కనుక్కొండి.
సాధన:
ఇక్కడ m₁ = M అయితే m₂ = 4 M, r = 10 సెం.మీ = 10^-1 మీ, F = 6.67 × 10^-7 N, G = 6.67 × 10^-11 Nm²kg^-2

∴ ఒక వస్తువు ద్రవ్యరాశి m = 5 కి.గ్రా, రెండవ వస్తువు ద్రవ్యరాశి m = 4 × 5 = 20కి. గ్రా

ప్రశ్న 3.
1కి.గ్రా, 2 కి.గ్రా మరియు 3కి. గ్రా ద్రవ్యరాశులు గల మూడు బంతులు 1 మీటరు భుజముగా గల ఒక సమబాహు త్రిభుజ మూడు శీర్షముల వద్ద ఉన్నవి. 1కి.గ్రా బంతిపై 2కి.గ్రా, 3కి.గ్రా ద్రవ్యరాశులు కలుగజేయు గురుత్వాకర్షణ బలం పరిమాణం ఎంత?
సాధన:

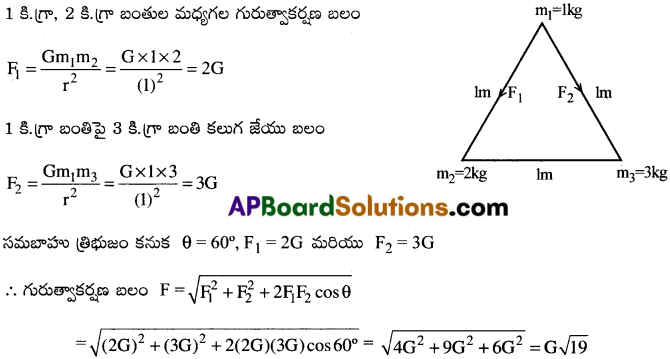
ప్రశ్న 4.
భూ ఉపరితలం నుండి కొంత ఎత్తులో గురుత్వత్వరణం విలువ భూమి ఉపరితలము పై ఉండు విలువలో 4% ఉన్నది .అయితే ఆ ఎత్తు ఎంత.
సాధన:

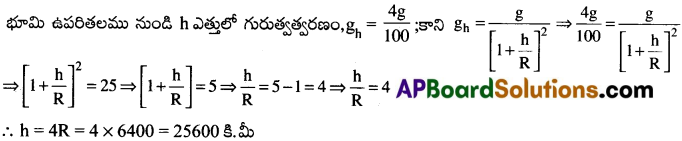
ప్రశ్న 5.
భూమి నుండి 1000 కి.మీ ఎత్తులో తిరుగుచున్న ఉపగ్రహం కక్ష్యా వేగం ఎంత?
సాధన:
ఇక్కడ h = 1000 కి.మీ, R = 6400 కి. మీ. Also, G = 6.67 × 10^-11 Nm²/kg², ME = 6 × 10²⁴kg

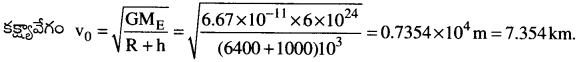
ప్రశ్న 6.
భూమి ఉపరితలం నుండి భూ వ్యాసార్థమునకు సమానమైన ఎత్తులో ఒక ఉపగ్రహం తిరుగుచున్నది. దాని i) కక్ష్యావేగమును ii) పరిభ్రమణ కాలమును కనుక్కోండి.
సాధన:
ఇక్కడ h = R = 6.4 × 10⁶ మీ. Also, G = 6.67 × 10^-11 Nm²/kg²; M_E = 6 × 10²⁴ కి. గ్రా

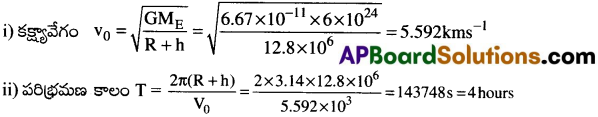
ప్రశ్న 7.
రెండు వస్తువుల మధ్య ఉన్న దూరమును 4 మీ పెంచిన వాని మధ్యగల గురుత్వాకర్షణ బలం 36% తగ్గును. అయిన వాని మధ్యగల తొలి దూరమును కనుక్కోండి.
సాధన:

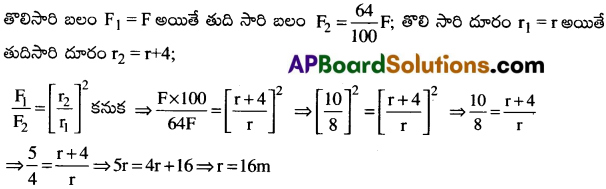
ప్రశ్న 8.
1 కి.గ్రా మరియు 4 కి.గ్రా. ద్రవ్యరాశులు గల రెండు బంతుల మధ్య దూరం 12 సెం.మీ. 1కి.గ్రా బంతి నుండి ఎంత దూరములో గల బిందువు వద్ద ఏ వస్తువు నుంచినా దానిపై ఫలిత గురుత్వాకర్షణ బలం శూన్యమగును.
సాధన:
ఇక్కడ m₁ = 1 kg; m₂ = 4 kg రెండు బంతుల మధ్యదూరం d = 12 cm

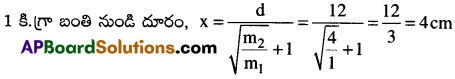
ప్రశ్న 9.
ఒక్కొక్కటిm ద్రవ్యరాశి గల నాలుగు కణములను a భుజముగా గల ఒక చతురస్రము నాలుగు శీర్షముల వద్ద ఉంచిరి. ఏదైనా ఒక కణము పై మిగిలిన మూడు కణముల ఫలిత గురుత్వాకర్షణ బలమును కనుక్కోండి.
సాధన:
m₁ = m₂ = m₃ = m₄ = m

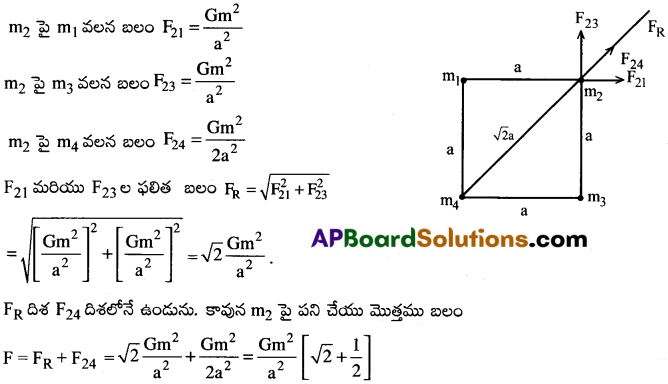
ప్రశ్న 10.
m ద్రవ్యరాశి R వ్యాసార్థము గల మూడు సర్వసమాన గోళములను, ఒకటి మిగతా రెండింటిని తాకునట్లుగా ఉంచిరి. ఏదైనా ఒక గోళము పై మిగిలిన రెండు గోళముల ఫలిత గురుత్వాకర్షణబలం ఎంత?
సాధన:
m₁ = m₂ = m₃ = m రెండు గోళముల మధ్యదూరం, r = 2R

ప్రశ్న 11.
రెండు ఉపగ్రహములు భూమి ఉపరితలము నుండి వేర్వేరు ఎత్తులలో తిరుగుచున్నవి. వాని కక్ష్యావేగముల నిష్పత్తి 2 : 1. అందులో ఒకటి 100 కి.మీ ఎత్తులో ఉన్న రెండవ దాని ఎత్తు ఎంత?
సాధన:

ప్రశ్న 12.
భూమి చుట్టూ ఒక ఉపగ్రహం కొంత ఎత్తులో 8 కి.మీసె^-2 వేగంతో పరిభ్రమించుచున్నది. ఆ ఎత్తు వద్ద గురుత్వ త్వరణం విలువ 8 ms^-2. భూమి వ్యాసార్థం 6000 కి.మీ అనుకుంటే ఆ ఉపగ్రహం భూమి ఉపరితలం నుండి ఎంత ఎత్తులో ఉన్నది?
సాధన:
ఇక్కడ కక్ష్యావేగం V₀ = 8 కి.మీ/సె = 8000మీ/సె, భూవ్యాసార్థం, R = 6000 కి.మీ = 6 × 10⁶ మీ, g_h = 8 మీ సె^-2.

ప్రశ్న 13.
(a) భూమి ఉపరితలముపై ఒక వస్తువునకు గల పలాయన వేగమును లెక్క కట్టండి. (b) భూమి చెక్కతో తయారై ఉన్నట్లయితే, దాని ద్రవ్యరాశి ప్రస్తుతము ఉన్న ద్రవ్యరాశిలో 10% ఉండేది. అపుడు భూ ఉపరితలముపై పలాయన వేగం ఎంత ఉండేది?
సాధన:
భూమి ద్రవ్యరాశి M = 6 × 10²⁴ కి.గ్రా; g = 9.8మీ సె^-2 భూమి వ్యాసార్థం R = 6400 కి.మీ = 6.4 × 10⁶ మీ