AP Inter 1st Year Physics Important Questions Chapter 8 డోలనాలు

Students get through AP Inter 1st Year Physics Important Questions 8th Lesson డోలనాలు which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 8th Lesson డోలనాలు

Very Short Answer Questions (అతిస్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
డోలనాత్మకం కాని ఆవర్తక చలనాలకు రెండు ఉదాహరణలు ఇవ్వండి.
జవాబు:

1. సూర్యుని చుట్టూ గ్రహాల భ్రమణము.
2. న్యూక్లియస్ చుట్టూ ఎలక్ట్రాన్ భ్రమణం.

ప్రశ్న 2.
సరళ హరాత్మక చలన స్థానభ్రంశాన్ని y=asin(20t+4) తో సూచించారు. కాలాన్ని 2T/O పెంచితే దాని స్థానభ్రంశం ఎంత? [Imp.Q]
జవాబు:
\(\frac{2 \pi}{\omega}\)అనునది ఆవర్తన కాలమునకు సమానము. ఆవర్తన కాలము గడిచిన పిమ్మట కణము అదే స్థానమునకు వచ్చును. కనుక స్థానభ్రంశము అంతే ఉండును.

ప్రశ్న 3.
ఒక బాలుడు ఊయలపై కూర్చుని డోలనాలు చేస్తున్నాడు. అతడు నిలబడితే పౌనఃపున్యం ఏ విధంగా మారుతుంది. [Imp.Q]
జవాబు:
బాలుడు నిలబడడం వలన లోలకం పొడవు తగ్గుతుంది. T ∝ √l కావున ఆవర్తనకాలం తగ్గుతుంది. పౌనఃపున్యం పెరుగుతుంది.

ప్రశ్న 4.
లఘు లోలకం గుండు నీటితో నిండిన ఒక బోలు గోళం. గోళం నుంచి నీరు కారిపోతుంటే దాని డోలనావర్తన కాలం ఏవిధంగా మారుతుంది?
జవాబు:
గోళము పూర్తిగా నీటితో నిండి ఉన్నపుడు, లఘులోలకం ఆవర్తన కాలం T అనుకొనుము. లోలకం ఆవర్తన కాలం లోలకము యొక్క పొడవుపై ఆధారపడి ఉండును. నీరు గోళము నుండి బయటకు పోవుచున్న కొలది లోలకం యొక్క ఫలిత పొడవు పెరుగుచుండును. అందువలన ఆవర్తన కాలం కూడా పెరుగుచుండును. నీరు పూర్తిగా బయటకు పోయిన తర్వాత లోలకం యొక్క ఫలిత పొడవు తొలి విలువకు సమానమగును. అందువలన ఆవర్తన కాలం కూడా తొలి విలువకు సమానమగును.

ఆధార బిందువు నుండి గోళము ద్రవ్యరాశి కేంద్రము వరకు గల దూరమును లోలకం పొడవు అని అంటారు. గోళము నుండి నీరు బయటకు పోవుచున్నపుడు (నీరు + గోళము) వ్యవస్థ యొక్క ద్రవ్యరాశి కేంద్రము క్రిందకు జరుగుచుండును. అందువలన లఘులోలకం యొక్క ఫలిత పొడవు పెరుగుచుండును. నీరు అంతయు బయటకు పోయిన తరువాత ద్రవ్యరాశి కేంద్రము తొలి స్థానమునకు వచ్చును.

ప్రశ్న 5.
లఘులోలకానికి కట్టిన చెక్క గుండుకు బదులు దాన్ని పోలి ఉండే అల్యూమినియం గుండును ఉపయోగిస్తే దాని ఆవర్తన కాలం ఏవిధంగా మారుతుంది?
జవాబు:
ఒక లఘులోలకం యొక్క ఆవర్తన కాలం గోళము యొక్క పదార్థముపై గాని, పరిమాణము పై గాని, ఆకారము పై గాని ఆధారపడి ఉండదు. కేవలం లోలకం పొడవుపై ఆధారపడి ఉండును. కావున చెక్క గోళమునకు బదులు అల్యూమినియం గోళమును ఉపయోగించినప్పటికి ఆవర్తన కాలములో మార్పురాదు.

ప్రశ్న 6.
లోలక గడియారాన్ని పర్వతంపైకి తీసుకొని వెళితే అది సమయాన్ని పొందుతుందా? కోల్పోతుందా? [Imp:Q]
జవాబు:
ఒక లఘులోలకం ఆవర్తన కాలం T = 2π\(\sqrt{\frac{l}{g}}\); లోలకం పొడవు స్థిరముగా ఉన్నపుడు, T ∝ \(\frac{l}{\sqrt{g}}\)

పర్వతము పైన g విలువ తక్కువగా ఉండును. (భూఉపరితలము పై పోల్చినపుడు). అందువలన ఆవర్తన కాలం (T) పెరుగును. అనగా ఒక కంపనము పూర్తి చేయుటకు పట్టు కాలము పెరుగును. అందువలన అది తక్కువ కంపనములు చేయును. కావున లోలకం సమయమును కోల్పోవును. అనగా లోలకం నిదానమగును.

ప్రశ్న 7.
ఒక లోలక గడియారం భూమధ్యరేఖ వద్ద సరియైన సమయమును సూచించుచున్నది. దానిని ధ్రువాల వద్దకు తీసుకొనిపోయిన అది సమయమును కోల్పోవునా లేక పొందునా? కారణమేమి? [Imp.Q]
జవాబు:
ఒక లఘులోలకం ఆవర్తన కాలం T = 2π\(\sqrt{\frac{l}{g}}\) లోలకం పొడవు స్థిరముగా ఉన్నపుడు, T ∝ \(\frac{l}{\sqrt{g}}\)

భూమధ్య రేఖ వద్ద కంటె ధ్రువాల వద్ద g విలువ అధికం. అందువలన లోలకమును భూమధ్యరేఖ వద్ద నుండి ధ్రువాల వద్దకు తీసుకొని పోయినపుడు దాని ఆవర్తనకాలం (T) తగ్గును. అనగా ఒక కంపనమును పూర్తి చేయుటకు పట్టు కాలము తగ్గును. కనుక అది ఎక్కువ డోలనములు చేయును. అందువలన అది ఎక్కువ సమయమును చూపును. అనగా గడియారం వేగం అయినది అని అంటారు.

ప్రశ్న 8.
స.హ.చ లోగల ఒక కణము స్థానభ్రంశము, దాని కంపన పరిమితిలో సగము ఉన్నపుడు, మొత్తము శక్తిలో గతిశక్తి ఎంత భాగం?
జవాబు:
కంపన పరిమితి A, కోణీయ వేగం ω, స్థానభ్రంశముy అయిన స.హ.చ. లో గల కణం రేఖీయ వేగం,

ప్రశ్న 9.
సరళ హరాత్మక డోలకం కంపన పరిమితిని రెట్టింపు చేస్తే దాని శక్తి ఏవిధంగా మారుతుంది? [Imp.Q]
జవాబు:
కంపన పరిమితి A, కోణీయ వేగం ω, ద్రవ్యరాశి m అయిన స.హ.చ. లో గల కణం మొత్తం శక్తి T.E = \(\frac{1}{2}\)mω²A² కావున కంపన పరిమితి A ని రెట్టింపు చేసిన మొత్తం శక్తి నాలుగు రెట్లు పెరుగును.

ప్రశ్న 10.
కృత్రిమ ఉపగ్రహంలో లఘులోలకాన్ని ఉపయోగించవచ్చా?
జవాబు:
కృత్రిమ ఉపగ్రహములో ఫలిత త్వరణం g = 0 లఘు లోలకం ఆవర్తన కాలం T = 2π\(\sqrt{\frac{l}{g}}\), కనుక T = అనంతం అగును. అనగా లఘు లోలకం కంపించదు. కాబట్టి ఒక లఘు లోలకమును కృత్రిమ ఉపగ్రహములో ఉపయోగించలేము.

Short Answer Questions (స్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
సరళ హరాత్మక చలనమును నిర్వచించండి. ఉదాహరణలతో వివరించండి.
జవాబు:
సరళ హరాత్మక చలనం :
ఒక ఆవర్తన చలనంలో, త్వరణం ఎప్పుడూ స్థానభ్రంశానికి అనులోమానుపాతంలో ఉంటూ; త్వరణం దిశ, స్థానభ్రంశ దిశకు వ్యతిరేక దిశలో ఉంటూ, త్వరణం దిశ ఎల్లప్పుడూ ఒక స్థిర బిందువు వైపుకు పనిచేస్తూ ఉండే చలనాన్ని సరళ హరాత్మక చలనం అంటారు.

సరళ హర్మాతక చలనంలో ఉన్న ఒక వస్తువు త్వరణం a అని, మధ్య బిందువు నుంచి దాని స్థానభ్రంశం x అని అనుకుంటే a∝ -x

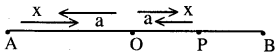
⇒ a = -kx,( k అనుపాత స్థిరాంకము)

ఇక్కడ ఋణ గుర్తు, స్థానభ్రంశం x మరియు త్వరణం a లు వ్యతిరేకదిశలో ఉండునని సూచించును.
ఉదా : 1) వృత్తవ్యాసము పై లంబ పాదము యొక్క చలనము.
2) స్వల్ప స్థానభ్రంశాలు గల లఘులోలకం డోలనాలు.
3) భార స్ప్రింగ్ డోలనాలు
4) u – గొట్టంలోని ద్రవస్తంభాన్ని నొక్కి వదిలితే, అది చేసే డోలనాలు.

ప్రశ్న 2.
స.హ.చ.లో గల కణం స్థానభ్రంశం, వేగం, త్వరణాలు కాలం ధృష్ట్యా మారే విధానాన్ని గ్రాఫ్ ద్వారా వివరించండి.
జవాబు:

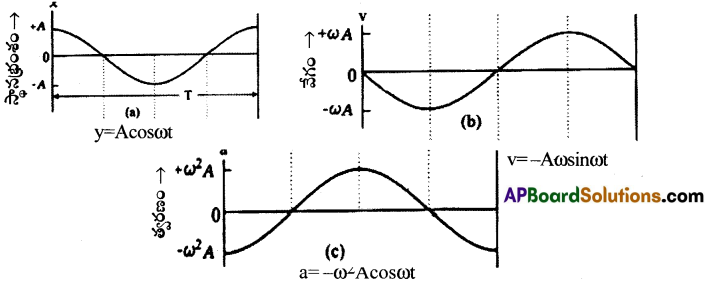
ప్రశ్న 3.
దశ లేక ప్రావస్థ అనగా ఏమి? స.హ.చ.లో గల ఒక కణం స్థానభ్రంశం, వేగం మరియు త్వరణం మధ్యగల ప్రావస్థ సంబంధములను వివరించండి.
జవాబు:
దశ: స.హ.చ.లో గల ఒక కణం స్థానభ్రంశం y = asinωt అనుకొనుము t కాలం వద్ద, దాని వేగం,

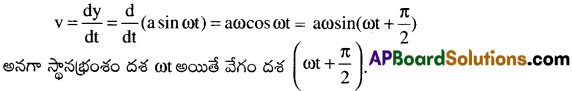
కావున స్థానభ్రంశమునకు, వేగమునకు దశా ‘భేదం = T/2 రేడియన్.
మరల త్వరణం a =\(\frac{dv}{dt}=\frac{d}{dt}\) (aωcos ωt) = -aω² sin ωt = -ω²y

కావున స్థానభ్రంశమునకు, త్వరణమునకు దశా భేదం = π రేడియన్
వేగమునకు, త్వరణమునకు దశాభేదం = π/2రేడియన్

ప్రశ్న 4.
ఒక స్ప్రింగ్ బలస్థిరాంకం k. దానికి ఒక చివర m ద్రవ్యరాశి గల వస్తువును తగిలించినపుడు అది చేయు కంపనముల పౌనఃపున్యమునకు ఒక సమీకరణమును ఉత్పాదించండి.
జవాబు:
‘m’ ద్రవ్యరాశి గల దిమ్మెను ధృడమైన ఆధారం నుండి భారరహిత స్ప్రింగ్ ద్వారా పటంలో చూపిన విధంగా వ్రేలాడ దీసి ఉన్నదనుకొనుము. దానిని కొద్దిగా కిందికి లాగి వదిలితే, అది సరళహరాత్మక చలనం చేస్తుంది.

దిమ్మె మీద పనిచేసే పునఃస్థాపక బలం ‘F’, స్థానభ్రంశానికి అనులోమానుపాతంలోనూ మరియు దిశలో వ్యతిరేకంగానూ ఉంటుంది.
∴ F ∝ -y
⇒ F = -ky ఇక్కడ k ను స్ప్రింగ్ బలస్థిరాంకం అంటారు.
కాని F = ma ∴ ma = – ky
⇒ a = (\(\frac{-k}{m}\))y ………….(1)

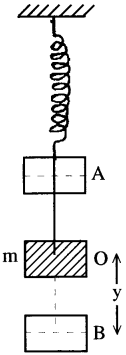
అనగా త్వరణం స్థానభ్రంశానికి అనులోమానుపాతంలో ఉంటూ, వ్యతిరేక దిశలో పనిచేస్తుంది. అందువల్ల డోలనాలు సరళహరాత్మకంగా ఉన్నాయంటాం.
1 వ సమీకరణాన్ని a = – ω²y తో పోల్చగా,

ప్రశ్న 5.
స.హ.చ.లో గల కణము గతిశక్తికి, స్థితిశక్తికి సమీకరణములను రాబట్టండి.
జవాబు:
స.హ.చ.లో గల కణము యొక్క స్థాన భ్రంశము y = A sinωt

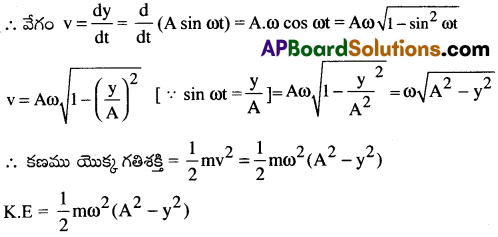
స్థితిశక్తికి సమీకరణం ఉత్పాదించుట :
పునఃస్థాపక బలం, స్థానభ్రంశానికి (y) వ్యతిరేకదిశలో ఉండటం వల్ల పున:స్థాపక బలాన్ని నిరోధిస్తూ జరిగే పని స్థితిశక్తి రూపంలో నిల్వ ఉంటుంది.

ప్రశ్న 6.
డోలనాలు చేసే లఘులోలకం ఒక అంత్యస్థానం నుంచి మరో అంత్యస్థానానికి చలించే సమయంలో శక్తి ఏవిధంగామారుతుంది?
జవాబు:
మొత్తం శక్తి ఎల్లప్పుడూ స్థిరం. చరమస్థానం వద్ద స్థితిశక్తి (P.E) గరిష్టం మరియు గతిశక్తి శూన్యం అవుతుంది. మాధ్యమిక బిందువు వద్ద గతిశక్తి గరిష్టం మరియు స్థితిశక్తి శూన్యం అవుతుంది. మిగిలిన బిందువుల వద్ద దాని శక్తి కొంత స్థితిశక్తి రూపంలోను, కొంత గతిశక్తిరూపంలోను ఉంటుంది.

ప్రశ్న 7.
స.హ.చ.లో గల కణం స్థానభ్రంశం, వేగం మరియు త్వరణములకు సమీకరణములను ఉత్పాదించండి.
జవాబు:
సరళ హరాత్మక చలనం :
ఒక ఆవర్తన చలనంలో, త్వరణం ఎప్పుడూ స్థానభ్రంశానికి అనులోమానుపాతంలో ఉంటూ త్వరణం దిశ, స్థానభ్రంశ దిశకు వ్యతిరేక దిశలో ఉంటూ, త్వరణం దిశ ఎల్లప్పుడూ ఒక స్థిర బిందువు వైపుకు పనిచేస్తూ ఉండే చలనాన్ని సరళ హరాత్మక చలనం అంటారు.

‘A’ వ్యాసార్థం గల వృత్తపరిధిపై సమకోణీయ వేగం ‘ω’తో గమనంలో ఉన్న కణం ‘P’ అనుకొనుము. కణం వృత్త పరిధిపై ఒక భ్రమణం పూర్తి చేసినపుడు ఆ కణం యొక్క లంబపాదం N, వృత్త వ్యాసంపై ఒక డోలనం చేస్తుంది. కణం ఏదైనా బిందువు ‘P’ వద్ద ఊహిస్తే,

Long Answer Questions (దీర్ఘ సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
సరళహరాత్మక చలనమును నిర్వచించండి. ఏకరీతి వృత్తాకార చలనం చేసే కణం విక్షేపం (ఏదైనా) వ్యాసంపై సరళ హరాత్మక చలనం చేస్తుందని చూపండి. [AP 19][AP,TS 18] [IPE’14][Imp.Q][TS 15,16,19]
జవాబు:
సరళ హరాత్మక చలనం: ఒక ఆవర్తన చలనంలో, త్వరణం ఎల్లప్పుడూ స్థానభ్రంశానికి అనులోమానుపాతంలో ఉంటూ, త్వరణం దిశ స్థానభ్రంశ దిశకు వ్యతిరేక దిశలో ఉంటూ, త్వరణం దిశ ఎల్లప్పుడూ ఒక స్థిర బిందువు వైపుకు పనిచేస్తూ ఉండే చలనాన్ని సరళ హరాత్మక చలనం అంటారు.

‘A’ వ్యాసార్థం గల వృత్తపరిధిపై సమకోణీయ వేగం ‘ఎ’తో గమనంలో ఉన్న కణం ‘P’ అనుకొనుము. కణం వృత్త పరిధిపై ఒక భ్రమణం పూర్తి చేసినపుడు ఆ కణం యొక్క లంబపాదం N, వృత్త వ్యాసంపై ఒక డోలనం చేస్తుంది. కణం ఏదైనా బిందువు ‘P’ వద్ద ఊహిస్తే,

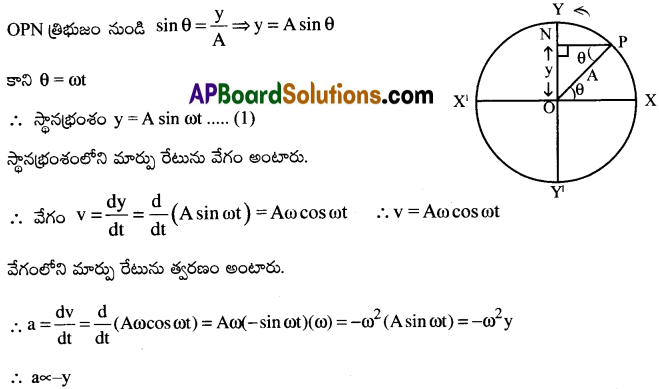
పైన చూపిన విధంగా వృత్తవ్యాసంపై ఏకరీతి వృత్తాకార గమనం సరళహరాత్మక చలనం.

ప్రశ్న 2.
లఘులోలకం చలనం సరళ హరాత్మకమని చూపించండి. లఘులోలకం డోలనావర్తన కాలానికి సమీకరణం ఉత్పాదించండి. సెకన్ల లోలకం అంటే ఏమిటి ? [AP 15,16,17,18,20,22][TS 15,16,17,18,20,22]
జవాబు:
‘m’ ద్రవ్యరాశి గల ఒక లోహపు గోళాన్ని ‘l’ పొడవు గల దారానికి ఒక చివర కట్టి ఆధారం నుండి వ్రేలాడదీయబడినది. ఏదైనా కాలంలో గోళం యొక్క కోణీయ స్థానభ్రంశం θ. గోళం భారం (mg) ను రెండు లంబాంశాలుగా విడగొట్టవచ్చు. దాని సమాంతరాంశం mg cosθ, తన్యత బలంకు మరియు లంబాంశం mg sinθ పునఃస్థాపక బలంకు సమానం.
∴ పునఃస్థాపక బలం F = -mg sinθ
కాని F = ma
∴ ma = -mg sinθ ⇒ a = -g sinθ
θ విలువ బాగా తక్కువైనప్పుడు sinθ = θ
∴ a = -g(θ)


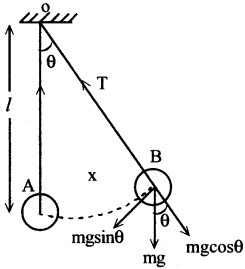
సెకన్ల లోలకం :
ఆవర్తన కాలం 2 సెకన్లుగా ఉన్న లోలకమును సెకన్ల లోలకం అందురు.

ప్రశ్న 3.
సరళహరాత్మక డోలకం గతిజ, స్థితిజ శక్తులకు సమీకరణాలను ఉత్పాదించండి. సరళ హరాత్మక చలనంలోని కణం పథంపై అన్ని బిందువుల వద్ద మొత్తం శక్తి స్థిరం అని చూపండి. [AP 19][Imp.Q]
జవాబు:
గతిజ శక్తి :
స.హ.చ. లో గల కణము యొక్క స్థాన భ్రంశము y = A sin ωt

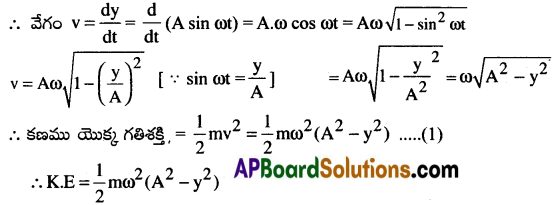
స్థితిజ శక్తి :
పునఃస్థాపక బలం, స్థానభ్రంశానికి (y) వ్యతిరేకదిశలో ఉండటం వల్ల పునఃస్థాపక బలాన్ని నిరోధిస్తూ జరిగే పని స్థితిశక్తి రూపంలో నిల్వ ఉంటుంది.
సరాసరి బలం = \(\frac{0+F}{2}=\frac{F}{2}\)

కావున సరళహరాత్మక డోలకం యొక్క సంపూర్ణ శక్తి స్థిరాంకమని, స్థానాన్ని మరియు కాలాన్ని బట్టి అది మారదని గ్రహించవచ్చు.
మాధ్యమిక బిందువు వద్ద T.E = K.E [∵ P.E = 0] మరియు
అంత్య బిందువుల వద్ద T.E P.E [∵ K.E = 0]

Solved Problems (సాధించిన సమస్యలు)

ప్రశ్న 1.
సగటున ఒక మనిషి గుండె నిమిషమునకు 75 సార్లు కొట్టుకొనును. (స్పందించును) అయిన దాని పౌనఃపున్యము, ఆవర్తన కాలం ఎంత? [AP 19][Imp.Q]
సాధన:
హృదయ స్పందన పౌనఃపున్యం = 75 / (1 నిమిషం) = 75 / (60సె) = 1.25 s^-1 = 1.25 Hz
ఆవర్తన కాలం T = 1/(1.25 s^-1) = 0.8 s.

ప్రశ్న 2.
ఈ క్రింది కాలప్రమేయములలో ఏవి (a)స.హ.చ (b) ఆవర్తన చలనమే కాని స.హ.చ కావు? ప్రతి సందర్భములో ఆవర్తన కాలము ఎంత?
(a) sinωt – cosωt (b) sin²ωt
సాధన:

ఇది ఆవర్తన చలనము కాని స.హ.చ కాదు. దీని ఆవర్తన కాలం, T = π/ω.

ప్రశ్న 3.
స.హ.చ చేయుచున్న ఒక కణము స్థానభ్రంశ సమీకరణము x = 5cos[2πt + π/4] SI ప్రమాణములు.
t = 1.5 సెకను వద్ద (a) స్థానభ్రంశము (b) వడి (c) త్వరణము కనుగొనుము.
సాధన:
కోణీయ వేగం = 2 π s^-1 ఆవర్తన కాలం T = 1s.
t = 1.5 s.వద్ద

ప్రశ్న 4.
సెకనుల లోలకం పొడవు ఎంత? [Imp.Q][AP 15,18][TS 15]
సాధన:

Exercise Problems

ప్రశ్న 1.
ఒక లఘులోలకం గుండు ఇత్తడితో చేసిన బోలు గోళము. దానిని పూర్తిగా నీటిని నింపిన లోలకం ఆవర్తనకాలం ఏమగును?
సాధన:
ఆవర్తన కాలములో మార్పు ఉండదు. నీటితో నింపినప్పటికి లోలకం యొక్క ఫలిత పొడవులో మార్పు ఉండదు. అందువలన ఆవర్తన కాలములో మార్పు ఉండదు.

ప్రశ్న 2.
‘K’ స్ప్రింగ్ స్థిరాంకం గల రెండు స్ప్రింగ్లను శ్రేణిలో కలిపిన ఫలిత స్ప్రింగ్ స్థిరాంకమును కనుక్కోండి.
సాధన:
స్ప్రింగ్ స్థిరాంకం ‘K’ గల రెండు స్ప్రింగ్లను శ్రేణిలో కలిపి, ‘mg’ అను భారమును ఆ సంయోగమునకు వ్రేలాడ దీసిరి అని అనుకొనుము. అపుడు ప్రతి స్ప్రింగ్ లోను పునఃస్థాపక బలం ‘F’=mg అగును. బల స్థిరాంకములు సమానం కావున స్ప్రింగ్లో కలుగు సాగుదలలు కూడ సమానముగా ఉండును. ఒక్కొక్క స్ప్రింగ్ లోని సాగుదల y అయితే మొత్తము సాగుదల 2y అగును.

పునఃస్థాపక బలం = బల స్థిరాంకం × సాగుదల కనుక
F = బల స్థిరాంకం × 2y
⇒ బల స్థిరాంకం = \(\frac{F}{2y}\) ……(1)
‘K’ బల స్థిరాంకం గల ఒక స్ప్రింగ్ను తీసుకొని దానికి m ద్రవ్యరాశి గల వస్తువును తగిలించిన, స్ప్రింగ్లో ఏర్పడు పునఃస్థాపక బలం, F = mg మరియు సాగుదల y అగును. కావున
K = \(\frac{F}{y}\) ………….. (2)

(1) మరియు (2), సమీకరణముల నుండి శ్రేణిలో కలిపిన స్ప్రింగ్ ఫలిత స్ప్రింగ్ స్థిరాంకం = \(\frac{K}{2}\)

ప్రశ్న 3.
స.హ.చలో మధ్యమ స్థానము వద్ద ఏ ఏ భౌతిక రాశుల విలువలు గరిష్టముగా ఉండును?
సాధన:
మధ్యమ స్థానము వద్ద, వేగం మరియు గతిశక్తి విలువలు గరిష్టముగా ఉండును.

ప్రశ్న 4.
స.హ.చలో గల ఒక కణమునకు, గరిష్ట వేగము విలువ సంఖ్యాత్మకముగా గరిష్ట త్వరణములో సగమునకు సమానమైన దాని ఆవర్తన కాలము ఎంత? [TS 15]
సాధన:
స.హ.చ లో గల కణము కంపన పరిమితి A మరియు కోణీయ వేగం ω అయిన గరిష్ట వేగం, v_max = Aω
గరిష్ట త్వరణం, a_max = Aω²

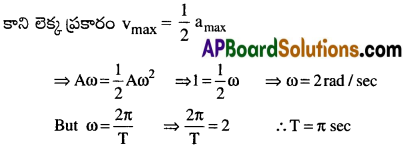
ప్రశ్న 5.
ఒక స్ప్రింగ్ యొక్క స్ప్రింగ్ స్థిరాంకం 260 Nm-1. దాని చివర 2 కి.గ్రా తగిలించిరి. అది 100 కంపనములు చేయుటకు పట్టు కాలం ఎంత? [TS 19]
సాధన:
స్ప్రింగ్కు తగిలించిన ద్రవ్యరాశి, m = 2 కి.గ్రా
స్ప్రింగ్ స్థిరాంకం, K = 260 Nm^-1
కంపనముల సంఖ్య, N = 100
100 కంపనములు చేయుటకు పట్టు కాలం (t) = ?
స్ప్రింగ్ లోలకమునకు ఆవర్తన కాలము, T = 2π\(\sqrt{\frac{m}{k}}\) ⇒ T = 2π\(\sqrt{\frac{2}{260}}\) = 2 × 3.14 × 0.088 = 0.55 sec
∴ 100 కంపనములు చేయుటకు పట్టు కాలం t = 100 × 0.55 = 55 సె

ప్రశ్న 6.
స్థిరముగా ఉన్న లిఫ్ట్లో ఉన్న ఒక లఘులోకం ఆవర్తన కాలం T. (i) లిఫ్ట్ సమవేగంతో పైకి పోవుచున్నపుడు (ii) సమవేగముతో క్రిందికి పోవుచున్నపుడు (iii) పైకి సమత్వరణం ‘a’ తో పోవుచున్నపుడు (iv) క్రిందికి సమత్వరణం ‘a’ తో పోవుచున్నపుడు (v) స్వేచ్ఛగా క్రిందికి పడుచున్నపుడు
సాధన:
లఘులోలకం ఆవర్తన కాలం, T = 2π\(\sqrt{\frac{l}{g}}\)
1. లిఫ్ట్ సమవేగముతో పైకి పోవుచున్నపుడు ఫలిత త్వరణములో మార్పు ఉండదు. కనుక దాని ఆవర్తన కాలములో మార్పు ఉండదు.
2. లిఫ్ట్ సమవేగముతో క్రిందికి పోవుచున్నపుడు కూడ ఫలిత త్వరణములో మార్పు ఉండదు. అందువలన T లో మార్పు ఉండదు.
3. లిఫ్ట్ ‘a’ అను సమత్వరణంతో పైకి పోవుచన్నపుడు, ఫలిత త్వరణం g+a అగును.

ప్రశ్న 7.
స.హ.చలో ఉన్న కణము కంపన పరిమితి 4 సెం.మీ కణము మధ్యమ స్థానము నుండి 1 సెం.మీ దూరములో ఉన్నపుడు దాని త్వరణం 3 సెం. మీ సె – 2 అయిన మధ్యమ స్థానము అది 2 సెం.మీ దూరములో ఉన్నపుడు దాని వేగం ఎంత?
సాధన:
కంపన పరిమితి (A) = 4 సెం.మీ
స.హ.చ.లో కణం స్థానభ్రంశం X అయితే దాని త్వరణం, a = ω²x (పరిమాణంలో )
లెక్క ప్రకారం a = 3సెం. మీసె^-2 మరియు x = 1సెం.మీ
∴ 3 = ω² × 1 ⇒ ω² = 3 ⇒ ω = √3 rad / sec

ప్రశ్న 8.
స.హ.చ.లో గల కణం ఆవర్తనకాలం 2 సెకన్లు. కణం మధ్యమ స్థానం దాటిన 0.25 సె తరువాత దాని దశ లేక ప్రావస్థ ఎంత?
సాధన:
ఆవర్తన కాలము, T = 2 సె
ఇచ్చిన కాలము, t = 0.25 సె
దశలోని తేడా = ?
T, = 2 సె అను ఆవర్తన కాలములో దశలో కలుగు మార్పు = 2π రేడియన్

ప్రశ్న 9.
స.హ.చలో గల కణం కంపన పరిమితి 5 సెం.మీ, ఆవర్తన కాలం 0.2 సె .కణం స్థానభ్రంశం (a) 5 సెం.మీ (b) 3 సెం.మీ (c) 0 సెం.మీ వద్ద దాని త్వరణం, వేగాలను కనుక్కోండి.
సాధన:
కణం కంపన పరిమితి (A) = 5 సెం.మీ= 5 × 10^-2 మీ
ఆవర్తన కాలం (T) = 0.2సెకను
(a) స్థానభ్రంశం = 5 సెం.మీ

ప్రశ్న 10.
ఒక గ్రహము ద్రవ్యరాశి, వ్యాసార్థము విలువలు భూమి విలువలకు రెట్టింపు. భూమి పై ఒక లఘులోలకం ఆవర్తనకాలం T అయితే ఆ గ్రహము మీద ఎంత? [AP 20]
సాధన:
భూమి ద్రవ్యరాశి = M భూమి వ్యాసార్ధము = R అయితే
గ్రహము ద్రవ్యరాశి = 2M గ్రహము వ్యాసార్థం = 2R
భూమి పై గురుత్వ త్వరణం, g_E = \(\frac{GM}{R^2}\)

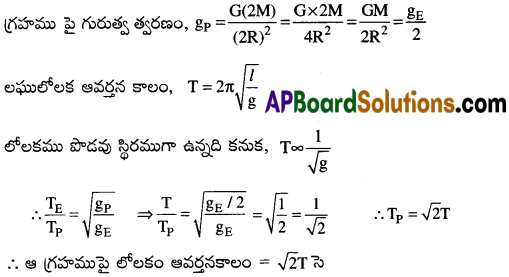
ప్రశ్న 11.
ఒక లఘులోలకం ఆవర్తనకాలం 2 సెకన్లు అయినపుడు దాని పొడవు 1 మీటరు. ఆవర్తన కాలం 1.5 సె అయితే లోలకం పొడవు లోని మార్పు ఎంత? [TS 18]
సాధన:
లోలకం తొలి పొడవు, l₁ = 1 మీ
తొలి ఆవర్తన కాలం T₂ = 2 సె
తుది ఆవర్తన కాలం T₂ = 1.5 సె
తుది పొడవు = l₂. అనుకొనుము
పొడవు లోని మార్పు = l₁ – l₂ = ?

ప్రశ్న 12.
ఒక గ్రహము మీద 8 మీటర్ల ఎత్తు నుండి స్వేచ్ఛగా పడుచున్న వస్తువు నేలను తాకుటకు 2 సెకన్లు తీసుకున్నది. గ్రహము మీద ఒక లోలకం ఆవర్తన కాలం T సెకను అయితే లోలకం పొడవు కనుక్కోండి.
సాధన:
స్వేచ్ఛగా పడుచున్న వస్తువునకు తొలి వేగం, u = 0
నేలను తాకుటకు పట్టిన కాలం t = 2s
ఎత్తు = ప్రయాణించిన దూరం (s) = 8m
ఆ గ్రహము పై గురుత్వత్వరణం (a) = g అనుకొనుము
s = ut + \(\frac{1}{2}\)at² ⇒ 8 = 0 + \(\frac{1}{2}\)g × 4 ⇒ 8 = 2g ⇒ g = 4ms-2
లఘులోలకం ఆవర్తన కాలం T = π s లఘులోలకం పొడవు, l = ?

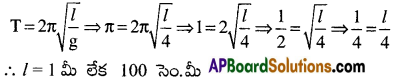
ప్రశ్న 13.
ఒక లఘులోలకం పొడవు 0.6 మీ. పెంచినపుడు ఆవర్తన కాలం 50% పెరిగినది. అయిన లఘులోలకం తొలి పొడవు, తొలి ఆవర్తన కాలము కనుక్కోండి. g = 9.8 ms-2,
సాధన:
లోలకం తొలి పొడవు = l అనుకొనుము
తుది పొడవు = (l + 0.6)m
లోలకం తొలి ఆవర్తన కాలం = T అనుకొనుము

ప్రశ్న 14.
ఒక సెకనుల లోలకం సరియైన సమయమును సూచించుచున్నది. వేసవి కాలములో దాని పొడవు 1.02 మీటరుకు పెరిగినది. అయిన ఒక రోజులో ఎంత సమయము ఎక్కువ లేక తక్కువ చూపును?
సాధన:
సెకనుల లోలకం ఆవర్తన కాలం T₁ = 2 సె ; సెకనుల లోలకం పొడవు l₁ = 1 మీ
వేసవి కాలములో లోలకం పొడవు, l₂ = 1.02 మీ; లోలకం కొత్త ఆవర్తన కాలం, T₂ = ?

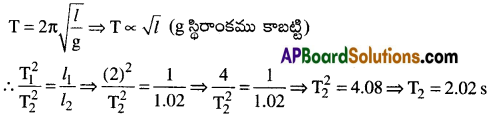
పొడవు పెరిగినది కనుక ఆవర్తన కాలము పెరిగినది. అందువలన అది తక్కువ కంపనములు చేయును. అందువలన గడియారం తక్కువ సమయమును చూపును.
లోలకం ఒక కంపనం పూర్తి చేయునప్పటికి తక్కువ చూపు కాలము = 2.02 – 2 = 0.02 సె

ఒక రోజులో ఒక సెకనుల లోలకం చేయు కంపనముల సంఖ్య \(\frac{86,400}{2}\) = 43,200
∴ 43200 కంపనములు పూర్తి చేయునప్పటికి తక్కువ చూపు కాలం = 43200 × 0.02 = 864
∴ అందువలన గడియారం రోజుకి 864 సెకన్లు తక్కువ చూపును.

ప్రశ్న 15.
ఒక స్ప్రింగ్ నుండి వ్రేలాడ దీసిన ఒక వస్తువు డోలనావర్తన కాలం T .ఆ స్ప్రింగ్ను రెండు సమాన భాగములు చేసి అదే వస్తువును (i) ఒక స్ప్రింగ్ ముక్క తగిలించినపుడు (ii) ఒకే సారి రెండు స్ప్రింగ్ ముక్కల నుండి వ్రేలాడ తీసినపుడు దాని ఆవర్తన కాలము ఎంతెంత ఉండును?
సాధన:
స్ప్రింగ్ యొక్క బల స్థిరాంకము K స్ప్రింగ్ నుండి వ్రేలాడ దీసిన m ద్రవ్యరాశి అయితే దాని ఆవర్తన కాలం
T = 2π\(\sqrt{\frac{m}{k}}\) ……….(1)
స్ప్రింగ్ను రెండు సమ భాగములు చేసినపుడు, ఒక్కొక్క స్ప్రింగ్ ముక్క బల స్థిరాంకం 2k అగును. అదే ద్రవ్యరాశిని వ్రేలాడదీసినపుడు