AP Inter 1st Year Physics Important Questions Chapter 6 Work, Energy and Power

Students get through AP Inter 1st Year Physics Important Questions 6th Lesson Work, Energy and Power which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 6th Lesson Work, Energy and Power

Very Short Answer Questions

Question 1.
State the conditions under which a force does no work.
Answer:
Work done W = \(\overline{\mathrm{F}}.\overline{\mathrm{S}}\) = |F||S|cosθ
Hence, if θ = 90° then cos 90° = 0 ⇒ W = 0

1. When force (F) and displacement (S) are mutually perpendicular then work done is zero.
2. Even though when force is applied, if displacement is zero then also work done W = 0.

Question 2.
Define Work, power and Energy. State their Si units. [Imp.Q]
Answer:
Work :
Work is said to be done, when a force acting on a body moves it, through some distance in the direction of the force

SI unit of Work : Joule
Power : The rate of doing work is called power
SI unit of Power : Watt.
Energy : The capacity to do work is called Energy.
SI unit of Energy : Joule

Question 3.
State the relation between the kinetic energy and momentum of a body. [Imp.Q]
Answer:

Question 4.
State the sign of work done by a force in the following.
a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
b) work done by gravitational force in the above case.
Answer:
a) Force applied by the man in the displacement of the bucket are in the same direction.
So work done by the man is positive.

b) Gravitational force is acting in the downward direction and bucket is moving in the upward direction. So, work done by the gravity is negative.

Question 5.
State the sign of work done by a force in the following. [Imp.Q]
a) Work done by friction on a body sliding down an inclined plane.
b) Work done by gravitational force in the above case.
Answer:
a) Friction always acts in a direction, opposite to the direction of motion.
Hence the work done is negative.

b) The work done is positive, because the angle between the gravitational force and displacement is acute.

Question 6.
State the sign of work done by a force in the following
(a) work done by an applied force on a body moving on a rough horizontal plane with uniform velocity.
(b) Work done by resistive force of air on a vibrating pendulum in bringing it to rest
Answer:
(a) The work done is positive because the applied force and displacement of the body are in the same direction.

(b) The work done is negative because resistive force of air on a vibrating pendulum always acts in a direction opposite to the direction of motion of pendulum.

Question 7.
State if each of the following statements are true (or) false. Give reasons to your answer.
(a) Total energy of a system is always conserved, no matter what internal and externa! forces on the body are present.
(b) The. work done by earth’s gravitational force in keeping the moon in its orbit for its one revolution is zero.
Answer:
(a) True. Total energy of an isolated system will be conserved, if all the forms of energy are taken into account. Energy in one form may be converted into another form, but total energy of the system remains constant.

(b) True. Because the gravitational force is conservative.

Question 8.
Which physical quantity remains constant. [Imp.Q]
(i) in an elastic collision (ii) in an inelastic collision?
Answer:
The total momentum and total K.E of the system remain constant in elastic collision.

The total momentum of the system only remains constant in an inelastic collision.

Question 9.
A body freely falling from a certain height ‘h’ after striking a smooth floor rebounds to a height h/2. What is the coefficient of restitution between the floor and the body? [TS 18][Imp.Q]
Answer:

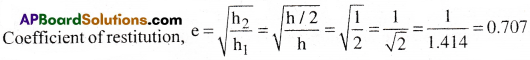
Question 10.
What is the total displacement of a freely falling body, after successive rebounds from the same place of ground, before it comes to stop? Assume that ‘e’ is the coefficient of restitution between the body and the ground?
Answer:
If h is the height from which the body is falling freely, then the total displacement is equal to ‘h’ only.

Short Answer Questions

Question 1.
What is potential energy? Derive an expression for the gravitational potential energy. [Imp.Q]
Answer:
Potential Energy: The energy possessed by a body by virtue of its position is called Potential energy.
Ex : Water in a Reservoir, Energy stored in a stretched rubber band.

Expression for P.E :
Consider a body of mass ‘m’, which is at rest on the surface of earth.
The Force acting on the body is equal to its weight mg.
Force required to lift the body upwards through a height ‘h’ is mg.
Now, Work done W = Force × displacement = mg × h = mgh
The work done is stored as P.E in the body.
∴ Potential Energy P.E = mgh

Question 2.
A lorry and a car moving with the same momentum are brought to rest by the application of brakes, which provide equal retarding forces. Which of them will come to rest in shorter time? Which will come to rest in less distance? [Imp.Q]
Answer:
(i) Given that, momentum is same for both lorry and car. Also, retarding forces are equal. Work done to stop the body = Change in Kinetic energy
F = ma ⇒ F = m(\(\frac{v-u}{t}\))
⇒ F × t = mv – mu
Both lorry and car are having same initial momentum, mu.
Both are finally stopped. So their final momenta(mv) are also same i.e, zero.
Their retarding forces (F) are also same. So they will be stopped in the same time.

(ii) Given that, momentum is same for both lorry and car. Also, retarding forces are equal.
Work done to stop the body = Kinetic energy

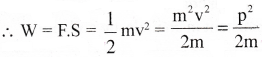
⇒ distance S ∝ \(\frac{1}{m}\) (Since, momentum and force are equal)
The heavier body (lorry) will come to rest in less distance.

Question 3.
Distinguish between conservative and non-conservative forces with one example each. [Imp.Q]
Answer:

Conservative force	Non – Conservative force
1) If the work done by a force around a closed path is zero, then such a force is called conservative force.	1) If the work done by a force around a closed path is a non-zero then such a force is called non-conservative force
2) The work done is independent of the path followed.	2) The work done depends on the path followed by the body.
3) Ex: Gravitational force.	3) Ex: Frictional force.

Question 4.
Show that in case of one dimensional elastic collision, the relative velocity of approach of two colliding bodies before collision is equal to the relative velocity of separation after collision. [AP 20; TS 18; May 08, Mar’07, Jun’06, Mar’05]
Answer:
Consider two spheres A and B of masses m₁ and m₂ moving with initial velocities u₁ and u₂ undergo a collision and after collision move with velocities v₁ and v₂ respectively.

According to law of conservation of momentum,
Total momentum before collision = Total momentum after collision.
m₁ u₁ + m₂u₂ = m₁v₁ + m₂v₂ ⇒ m₁u₁ – m₁v₁ = m₂v₂ – m₂u₂.
m₁(u₁ -v₁) = m₂(v₂ – u₂) ………. (1)
From the law of conservation of K.E

Thus,
Relative velocity of approach before collision = Relative Velocity of Separation after collision.

Question 5.
Show that two equal masses undergoing oblique elastic collision will move at right angles after collision, if the second body is initially at rest.
Answer:

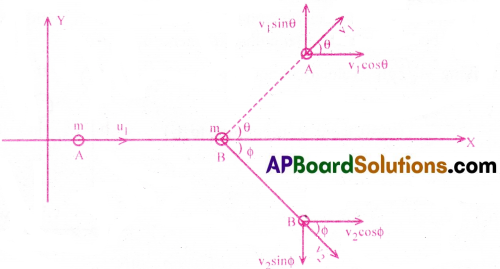
Let A and B be two particles which have an elastic oblique (non-head on) collision with each other, the particle B being at rest. The particle A is called the incident particle and the particle B is called target particle.
Let m be the mass of each particle. Let the velocity of A before collision is u₁.
∴ Total momentum of A and B before collision along X-axis = mu₁ + 0 = mu₁.

Total momentum of A and B before collision along Y-axis = 0 + 0 = 0 (because in Y-direction there are no velocity components)

Let v₁, v₂ be the velocities of A and B after collision.
Since the collision is oblique, let v₁ and v₂ make angles θ and Φ respectively with X-axis as shown in the figure.

From the law of conservation of momentum.
Total momentum before collision = Total momentum after collision.

Thus the two identical particles move at right angles after elastic oblique collision.

Question 6.
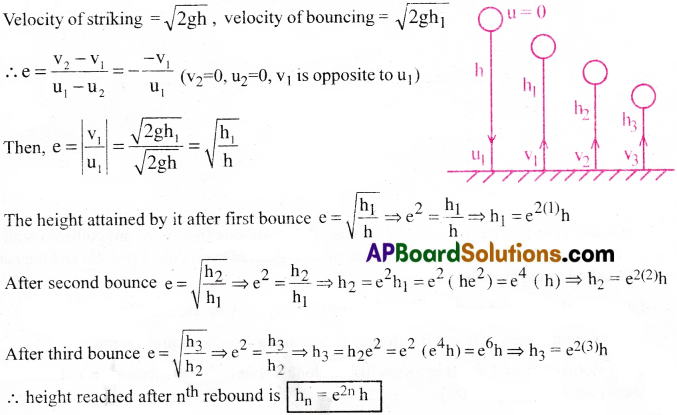
Derive an expression for the height attained by a freely falling body after ‘n’ number of rebounds from the floor.
Answer:
Consider a ball dropped onto the floor from a height ‘h’.
Suppose it hits the floor with a velocity u, and rebounds to a height ‘h₁’, with a velocity v₁
The velocity of the body before and after collision is zero (u₂ = v₂ = 0)

Question 7.
Explain the law of conservation id’ energy [Imp.Q]
Answer:
The total mechanical energy of a system is conserved if the forces doing work on it are conservative. If some of the forces involved are non-conservative, part of the mechanical energy may get transformed into other forms such as heat, light and sound. However, the total energy of an isolated system does not change, as long as one accounts for all forms of energy.

Energy may be transformed from one form to another form but total energy of an isolated system remains constant. Energy can neither be created nor destroyed. This law is called law of conservation of energy.

Long Answer Questions

Question 1.
Develop the notions of work and kinetic energy and show that it leads to work-energy theorem. [IPE’ 14; Imp.Q; TS 15, 19, 22; AP 17]
Answer:
Work :
The product of ‘force component along the displacement’ and magnitude of this displacement is called work.

Formula:
Work W= (F cosθ)S = FS cosθ
Kinetic Energy :
The energy possessed by a body by virtue of its motion is called Kinetic energy.

Formula:
Kinetic Energy, K = \(\frac{1}{2}\)mv²

Work-energy theorem :
The work done by a net force acting on a body is equal to change in its Kinetic Energv. Thus, W = \(\frac{1}{2}\)mv² – \(\frac{1}{2}\)mu²

Proof :
Let a body of mass‘m’ is moving with an initial velocity u.

Let a constant force F acts on the body, then it attains a final velocity v after time ‘t’

We know, Acceleration a = \(\frac{v-u}{t}\) …….. (1)
Displacement S = Average velocity × time ⇒ S = (\(\frac{v+u}{2}\))t …………. (2)
Now, Work done W = Force × displacement ⇒ W = FS = (ma)S …………. (3)
Substituting (1) and (2) in (3), we get

Question 2.
What arc collisions? Explain the possible types of collisions? Develop the theory of one dimensional elastic collision. [TS 22; AP 19, 20, 22; Imp.Q]
Answer:
Collision:
A strong interaction between two bodies that occur for a very short interval of time during which redistribution of momenta occurs is called collision.
If two bodies colllide in a short time interval then
(i) Velocities of colliding bodies change
(ii) Total Momentum will be conserved
(iii) Total Kinetic energy will be changed or conserved

Types of collisions :
(i) Elastic collision
(ii) Inelastic collision (Perfect, Partial)

(i) Elastic collision :
The collision in which both Momentum and Kinetic energy are conserved, is known as elastic collision.
Ex : Collision between two smooth Billiard balls, collisions between gas molecules

(ii) Inelastic collision :
The collision in which only Momentum is conserved but not kinetic energy, is called as inelastic collision.
Ex: Flitting a ball with a bat, collision between a bullet and its target

One dimensional elastic collisions :
If the velocities of colliding bodies, are confined along a straight line, before and after the collision, then such collisions are called “one dimensional collisions” (or) “head-on collisions”.

Consider two spheres of masses m₁ and m₂ moving with initial velocities u₁ and u₂ undergo an elastic collision. Let v₁, v₂ be the velocities after collision.

As the collision is elastic, law of conservation of linear momentum and kinetic energy are obeyed. From the law of conservation of momentum.

Total momentum before collision = Total momentum after collision.
⇒ m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ ⇒ m₁(u₁ – v₁) = m₂(v₂ – u₂) —— (1)
From the law of conservation of K.E,

Question 3.
State and prove law of conservation of energy in case of freely failing body. [Mar 13, May 13; AP, TS 15, 16, 17, 18, 19, 20]
Answer:
Law of conservation of energy :
Energy can neither be created nor be destroyed. It can be converted from one form to another form, (or)
Total energy remains constant in a closed system.

Proof :
Consider a freely falling body of mass ‘m’ released from a point ‘A’.
It is at a height ‘h’ above the ground, as shown in the figure.

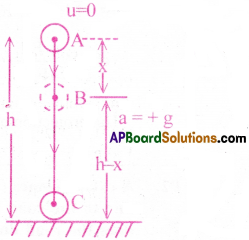
At Point A:
Potential Energy EE = mgh
At A, velocity is v_A = u = 0
Here, Kinetic Energy K.E = \(\frac{1}{2}\) mv²_A = \(\frac{1}{2}\)m(0)² = 0
∴ Total Energy T.E = P.E + K.E = mgh + 0 = mgh ……… (1)

At Point B:
Let the body travels a distance x and reaches the point B.
Now, the height of the body from the ground is (h – x)
∴ P.E = mg(h – x) = mgh – mgx
At the point B, we have, s = x, u = 0, v = v_B, a = +g

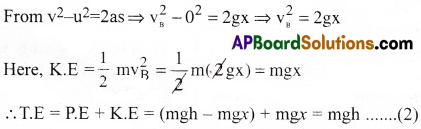
At Point C:
Let the body hits the ground at C Here, h = 0
∴ P.E = mgh = mg (0) = 0,
At the point C, we have, s=h, u=0, v=vc, a= +g

∴ T.E = P.E + K.E = 0 + mgh = mgh ……… (3)
From (1) ,(2), (3) it is clear that the total energy T.E is always constant.
Thus, the law of conservation of energy is verified.

Solved Problems

Question 1.
Find the angle between force \(\overline{\mathrm{F}}=(3\overline{\mathrm{i}}+4\overline{\mathrm{j}}-5\overline{\mathrm{k}})\) unit and displacement \(\overline{\mathrm{d}}=(5\overline{\mathrm{i}}+4\overline{\mathrm{j}}+3\overline{\mathrm{k}})\) unit. Also find the projection of \(\overline{\mathrm{F}}on\overline{\mathrm{d}}\)
Solution:

Question 2.
A cyclist conies to a skidding stop in 10m. During this process, the force on the cycle due to the road is 200N and is directly opposed to the motion, (a) How much work does the road do on the cycle? (b) How much work does the cycle do on the road?
Solution:
(a) The stopping force and the displacement make an angle of 180° with each other.
Thus, work done by the road,
W_r = Fd cosθ = 200 × 10 × cos 180° = -2000 J

(b) From Newton’s Third law, an equal and opposite force act on the road due to the cycle. Its magnitude is 200N. However, the road undergoes no displacement. Thus, work done by cycle on the road is zero.

Question 3.
In a ballistics demonstration, a police officer fires a bullet of mass 50.0g with speed 200 ms^-1 on soft plywood of thickness 2.00cm. The bullet emerges with only 10% of its initial kinetic energy. What is the emergent speed of the bullet? [TS 15]
Solution:
The initial kinetic energy of the bullet = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × (50 × 10^-3) × (200)² = 1000J
Final kinetic energy = 0.1 × 1000= 100J.
If v_f is the emergent speed of the bullet, then

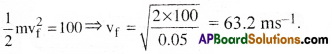
Question 4.
An elevator can carry a maximum load of 1800 kg (elevator + passengers) is moving up with a constant speed of 2 ms^-1. The frictional force opposing the motion is 4000N. Determine the minimum power delivered by the motor to the elevator in watt as well as in horse power. [TS 17]
Solution:
The downward force on the elevator is F = mg + F_f = (1800 × 10) + 4000 = 22000N
The motor must supply enough power to balance this force.
Hence, P = F.v = (22000)2 = 44000 W = \(\frac{44000}{746}\) ≈ 59HP ( 1 hp = 746W)

Exercise Problems

Question 1.
A test tube of mass 10 grams closed with a cork of mass 1 gram contains some ether. When the test tube is heated the cork Hies out under the pressure of the ether gas. The test tube is suspended horizontally by a weight less rigid bar of length 5cm. What is the minimum velocity with which the cork should fly out of the tube, so that test tube describing a full vertical circle about the point O. Neglect the mass of ether.
Solution:
Mass of test tube, mT = 10 g = 10 × 10^-3 kg
Mass of cork, mc = 1 g = 1 × 10^-3 kg
length of rod = radius of circular orbit = r = 5cm = 5 × 10^-2 m
The test tube will complete a full vertical circle if its velocity (V_T) is minimum and equal to √5gr

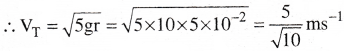
Before heating, cork and test tube are at rest. So their total linear momentum is zero. According to law of conservation of linear momentum, their total linear momentum after heating must also be equal to zero.
momentum of cork = momentum of test tube

Question 2.
A machine gun fires 360 bullets per minute and each bullet travels with a velocity of 600 ms^-1. If the mass of each bullet is 5gm, find the power of the machine gun? [IPE’ 13, 13, 14][AP 15, 16, 18, 19; TS 18]
Solution:
Mass of each bullet (m) = 5gm = 5 × 10^-3 kg
Velocity of each bullet (v) = 600 ms^-1
No. of bullets (n) = 360; Time (t) = 1 minute = 60 s; Power (p) =?

Question 3.
Find the useful power used in pumping 3425m³ of water per hour from a well 8m deep to the surface, supposing 40% of the horse power during pumping is wasted. What is the horse power of the engine?
Solution:
Volume of water lifted, V = 3425 m³.
Density of water ρ = 1000 kg/m³ = 10³ kg/m³.
mass of water lifted, m = V × ρ = 3425 × 10³ kg
Height through which water was raised (h) = 8m
Acceleration due to gravity (g) = 9.8 ms^-2
Work done by the pump in one hour = mgh = 3425 × 10³ × 9.8 × 8 = 268520 × 10³J

Question 4.
A pump is required to lift 600kg of water per minute from a well 25m deep and to eject it with a speed of 50ms^-1. Calculate the power required to perform the above task? [AP 15, 18; TS 16, 19, 20, 22]
Solution:
Mass of water lifted (m) = 600kg
depth of well (h) = 25m
Work done to lift water (W₁) = mgh = 600 × 9.8 × 25 = 147000 J
Speed of water (v) = 50ms^-1
Mass of water (m) = 600kg

Question 5.
A block of mass 5kg initially at rest at the origin is acted on by a force along the X- positive direction represented bv F = (20 + 5x)N. Calculate the work done by the force during the displacement of the block from x = 0 to x = 4m.
Solution:
Mass of the body (m) = 5kg
Force on the body (F) = (20 + 5x)N
Amount of work done to move the body by a small distance dx is dw = Fdx
Total work done to move the body from x = 0 to x = 4 is

Question 6.
A block of mass 5kg is sliding down a smooth inclined plane as shown. The spring arranged near the bottom of the inclined plane has a force constant 600 N/m. Find the compression in the spring at the moment the velocity of the block is maximum?
Solution:

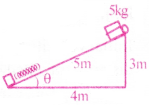
Given that m = 5 kg, K = 600 N/m, g = 10m/s², compression x = ?
From the diagram, sinθ = 3/5
From Newton’s third law, force due to block on spring F_B
= – Restoring force of spring F_R [∵ Action = – Reaction]
Hence, F_B = F_R ⇒ mgsinθ = Kx.
⇒ 5 × 10 × \(\frac{3}{5}\) = 600 × x
⇒ 5 × 10 × \(\frac{3}{5}\) = 600 × x ⇒ x = \(\frac{30}{600}\) = 0.05m = 5cm

Question 7.
A force F = –\(\frac{k}{x^2}\)(x ≠ 0) acts on a particle along the X-axis. Find the work done by the force in displacing the particle from x = +a to x = +2a. Take K as a positive constant.
Solution:
Given force F = \(\frac{-k}{x^2}\)(x ≠ 0)

Question 8.
A force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x = -a to x = +2a?

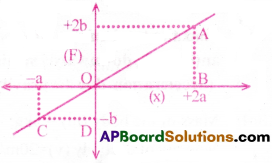
Solution:
Total work done = Area of the graph
= Area of triangle OAB + Area of triangle OCD

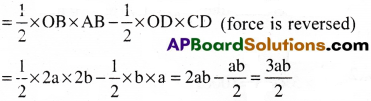
Question 9.
From a height of 20m above a horizontal floor, a ball is thrown down with initial velocity 20 m/s. After striking the floor, the ball bounces to the same height from which it was thrown. Find the coefficient of restitution for the collision between the ball and the floor? (g = 10m/s²)
Solution:
Initial velocity of the ball while coming downwards, u=20ms^-1.
distance travelled, s = h = 20m
Velocity of the ball at the time of hitting the ground v = ?
v² – u² = 2as ⇒ v² – 400 = 2 × 10 × 20

Question 10.
A ball falls from a height of 10m onto a hard horizontal floor and repeatedly bounces. If the coefficient of restitution is 1/√2 . What is the total distance travelled by the ball before it ceases to rebound?
Solustion:

Question 11.
Find the total energy of a body of 5kg mass, which is at a height of tOni from the earth and falling downwards straightly with a velocity of 20m/s.
(acceleration due to gravity as 10m/s²) [TS 16]
Solution:
Mass of the body (m) = 5kg;
Height of the body (h) = 10m
Velocity of the body (v)=20m/s,
Acceleration due to gravity (g) = 10 m/s
Potential Energy mgh= 5 × 10 × 10 = 500 J

Kinetic Energy = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 5 × (20)² = \(\frac{1}{2}\) × 5 × 400 = 1000J
∴ Total energy = P.E + K.E = 500 + 1000 = 1500J

Multiple Choice Questions

Question 1.
The power of a pump which can pump 100kg of water in 10s to a height of 100m is
1) 9800 W
2) 980 W
3) 98 W
4) 8800 W
Answer:
1) 9800 W

Question 2.
The work done in holding 15 Kg suitcase while waiting for a bus for 15 minutes is
1) 0
2) 1 J
3) 2 .1
4) 4 J
Answer:
1) 0

Question 3.
There are ……….. ergs in a Kwh
1) 3.6 × 10¹⁰
2) 3.6 × 10¹¹
3) 3.6 × 10¹²
4) 3.6 × 10¹³
Answer:
4) 3.6 × 10¹³

Question 4.
Two bodies of masses m₁ and m₂ have equal momenta. Their kinetic energies E₁ and E₂ are in the ratio

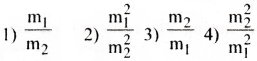
Answer:
3

Question 5.
A stone is projected vertically up to reach a maximum height h. The ratio of its kinetic energy to potential energy at a height 4h/5 will be
1) 5 : 4
2) 4 : 5
3) 1 : 4
4) 4 : 1
Answer:
3) 1 : 4

Question 6.
Two bodies of masses 2m and m have their kinetic energies in the ratio 8 : 1, then the ratio of their momenta is
1) 1 : 1
2) 2 : 1
3) 4 : 1
4) 8 : 1
Answer:
3) 4 : 1

Question 7.
If the speed of a vehicle increases by 2ms^-1, its kinetic energy is doubled, then original speed of the vehicle is

Answer:
3

Question 8.
One-fourth chain is hanging down from a table. Working done to bring the hanging part of the chain on the table is (mass of chain = M and length = L)

Answer:
1

Question 9.
A shell initially at rest explodes into two pieces of equal mass. The two pieces will
1) be at rest
2) move with different velocities in different directions.
3) move with same velocity in the opposite directions
4) move with same velocity in the same direction
Answer:
3) move with same velocity in the opposite directions

Question 10.
A 2Kg ball moving at 10ms^-1 collides with another 2Kg ball at rest. After collision they move together with
1) 5ms^-1 in the opposite direction
2) 5ms^-1 in the same direction
3) 10ms^-1 in the oppossite direction
4) 10ms^-1 in the same direction
Answer:
2) 5ms^-1 in the same direction

Question 11.
A particle falls from a height ‘h’ up on a fixed horizontal plane and rebounds. If ‘e’ is the coefficient of restitution, the total distance travelled before rebounding has

Answer:
1

Question 12.
A body falling from height of 10m rebounds from hard floor. If it loses 20% energy in impact, the coefficient of restitution is
1) 0.89
2) 0.56
3) 0.23
4)0.18
Answer:
1) 0.89

Question 13.
If a vector \(2\hat{i}+3\hat{j}+8\hat{k}\) is perpendicular to the vector \(4\hat{i}+4\hat{j}+\alpha\hat{k}\) then the value of α is
1) 1/2
2) -1/2
3) 1
4) -1
Answer:
2) -1/2

Question 14.
The angle between the two vectors \(\overrightarrow{A}=3\hat{i}+4\hat{j}+5\hat{k}\) and \(\overrightarrow{B}=3\hat{i}+4\hat{j}-5\hat{k}\) will be
1) 90°
2) 180°
3) zero
4)45°.
Answer:
1) 90°

Question 15.
A particle moves from a point \((-2\hat{i}+5\hat{j})\) to \((4\hat{j}+3\hat{k})\) when a force of \((4\hat{i}+3\hat{j})\)N is applied. How much work has been done by the force?
1) 8 J
2) 11 J
3) 5 J
4) 2 J
Answer:
3) 5 J

Question 16.
A uniform force of \((3\hat{i}+\hat{j})\) newton acts on a particle of mass 2 kg. Hence the particle is displaced from position \((2\hat{i}+\hat{k})\) metre to position \((4\hat{i}+3\hat{j}-3\hat{k})\) metre. The work done by the force on the particle is
1) 13 J
2) 15 J
3) 9 J
4) 6 J
Answer:
3) 9 J

Question 17.
A body moves a distance of 10 m along a straight line under the action of a 5 N force. If the w ork done is 25.1, then angle between the force and direction of motion of the body is
1) 60°
2) 75°
3) 30°
4) 456
Answer:
1) 60°

Question 18.
If \(\overrightarrow{F}=(60\hat{i}+15\hat{j}-3\hat{k})\) N and \(\overrightarrow{v}=(2\hat{i}-4\hat{j}+5\hat{k})\) ms^-1, then instantaneous power is
1) 195 watt
2) 45 watt
3) 75 watt
4) 100 watt
Answer:
2) 45 watt

Question 19.
Flow much water a pump of 2 kW can raise in one minute to a height of 10 m? (take g = 10 ni/s²)
1) 1000 litres
2) 1200 litres
3) 100 litres
4) 2000 litres
Answer:
2) 1200 litres

Question 20.
300 J of work is done in sliding a 2 kg block up an inclined plane of height 10 m. Work done against friction is (Take g = 10 m/s²)
1) 1000J
2) 200 J
3) 100 J
4) zero.
Answer:
3) 100 J

Question 21.
Water falls from a height of 60 m at the rate of 15 kg/s to operate a turbine. The losses due to frictional force are 10% of the input energy. How much power is generated by the turbine? (g = 10 m/s²)
1) 7.0 kW
2)10.2 kW
3) 8. 1 kW
4) 12.3 kW
Answer:
3) 8. 1 kW

Question 22.
Two bodies with kinetic energies in the ratio of 4:1 are moving with equal linear momentum. The ratio of their masses is
1) 4 : 1
2) 1 : 1
3) 1 : 2
4) 1 : 4
Answer:
4) 1 : 4

Question 23.
Two bodies of masses m and 4m are moving with equal kinetic energies. The ratio of their linear momenta is
1) 1 : 2
2) 1 : 4
3) 4 : 1
4) 1 : 1.
Answer:
1) 1 : 2

Question 24.
Two masses of 1 g and 9 g are moving with equal kinetic energies. The ratio of the magnitudes of their respective linear momenta is
1) 1 : 9
2) 9 : 1
3) 1 : 3
4) 3 : 1
Answer:
3) 1 : 3

Question 25.
A stationary particle explodes into two particles of masses m₁ and m₂ which move in opposite directions with velocities v₁ and v₂. The ratio of their kinetic energies E₁/E₂ is
1) m₂/m₁
2) m₁/m₂
3) 1
4) m₁v₂/m₂v₁
Answer:
1) m₂/m₁

Question 26.
A ball of mass 2 kg and another of mass 4 kg are dropped together from a 60 feet tall building. After a fall of 30 feet each towards earth, their respective kinetic energies will be in the ratio of
1) √2 : 1
2) 1 : 4
3) 1 : 2
4) 1 : √2
Answer:
3) 1 : 2

Question 27.
A particle of mass m₁ is moving with a velocity v₁ and another particle of mass m₂ is moving with a velocity v₂. Both of them have the same momentum but their different kinetic energies are E₁ and E₂ respectively If m₁ > m₂ then

Answer:
1

Question 28.
A particle is projected making an angle of 45° with horizontal having kinetic energy K, The kinetic energy at highest point will be
1) K/√2
2) K/2
3) 2K
4) K
Answer:
2) K/2

Question 29.
A shell of mass 200 gm is ejected from a gun of mass 4 kg by an explosion that generates 1.05 kJ of energy. The initial velocity of the shell is
1) 40 ms^-1
2) 120 ms^-1
3) 100 ms^-1
4) 180 ms^-1
Answer:
3) 100 ms^-1

Question 30.
A bullet of mass 10 g leaves a rifle at an initial velocity of 1000 m/s and strikes the earth at the same level with a velocity of 500 m/s. The work done in joule for overcoming the resistance of air will be
1) 375
2) 3750
3) 5000
4) 500
Answer:
2) 3750

Question 31.
A position-dependent force, F = (7 – 2x + 3x²) N acts on a small body of mass 2 kg and displaces it from x = 0 to y = 5 m. The work done in joule is
1) 135
2) 270
3) 35
4) 70
Answer:
1) 135

Question 32.
A force acts on a 3 g particle in such a way that the position of the particle as a function of time is given by x = 3t – 4t² + t³ where x is in metres and t is in seconds. The work done during the first 4 second is
1) 490 mJ
2) 450 mJ
3) 240 mJ
4) 530 mJ
Answer:
3) 240 mJ

Question 33.
Force F on a particle moving in a straight line varies with distance d as shown in figure. The work done on the particle during its displacement of 12m is

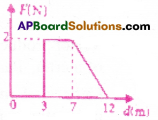
1) 18 J
2) 21 J
3) 26 J
4) 13 J
Answer:
4) 13 J

Question 34.
When a body moves with a constant speed along a circle
1) no work is done on it
2) no acceleration is produced in it
3) its velocity remains constant
4) no force acts on it.
Answer:
1) no work is done on it

Question 35.
The potential energy of a system increases if work is done
1) upon the system by a nonconservative force
2) by the system against a conservative force
3) by the system against a nonconservative force
4) upon the system by a conservative force.
Answer:
2) by the system against a conservative force

Question 36.
The coefficient of restitution e for a perfectly elastic collision is
1) 1
2) 0
3) ∞
4) -1
Answer:
1) 1

Question 37.
Two equal masses m₁ and m₂ moving along the same straight line with velocities + 3 m/s and -5 m/s respectively collide elastically. ‘Their velocities after the collision will be respectively
1) – 4 m/s and +4 m/s
2) +4 m/s for both
3) -3 m/s and +5 m/s
4) -5 m/s and +3 m/s
Answer:
4) -5 m/s and +3 m/s