AP Inter 1st Year Physics Important Questions Chapter 14 Kinetic Theory

Students get through AP Inter 1st Year Physics Important Questions 14th Lesson Kinetic Theory which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 14th Lesson Kinetic Theory

Very Short Answer Questions

Question 1.
Define mean free path.
Answer:
The mean free path is the average distance covered by a molecule between two successive collisions.

\(\vec{B}\) Where n’s the number density and d is the diameter of the molecule.

Question 2.
Name two prominent phenomena which provide conclusive evidence of molecular motion.
Answer:
Two prominent phenomena which provide conclusive evidence of molecular motion are

1. Diffusion
2. Brownian motion

Question 3.
How does kinetic theory justify Avogadro’s hypotheis and show that Avogadro Number in different gases is same?
Answer:
Consider same values of P, V and T for different gases. R is a universal gas constant which is also same for different gases. Then it follows from n = \(\frac{PV}{RT}\) that ‘n’ is same for different gases. This confirms Avogadro’s hypothesis. The number of molecules in 22.4 litres of any gas is 6.2 × 10²³. This is known as Avogadro number.

Question 4.
When does a real gas behave like an ideal gas? [AP 22][IPE’ 14] [TS 15, 16, 18, 19, 22]
Answer:
At low pressure and high temperature, a real gas behaves like an ideal gas.

Question 5.
State Boyle’s law and Charles law’.
Answer:
Boyle’s law :
At constant temperature(T), the Pressure (P) of a given mass of gas is inversely proportional to its Volume (V). P ∝ \(\frac{1}{V}\) ,(T is constant) (or) PV = Constant,

Charles law :
At constant pressure(P), the volume (V) of a given mass of a gas is directly proportional to its temperature(T) on Kelvin scale.
V ∝ T, ( P is constant) (or) \(\frac{V}{T}\) = Constant

Question 6.
State Dalton’s law of partial pressures.
Answer:
Dalton’s law of partial pressures states that total pressure of a mixture of ideal gases is sum of partial pressures.
P = P₁ + P₂ + P₃ + —– where P₁, P₂, P₃ are partial pressures.

Question 7.
Pressure of an ideal gas in container is independent of shape of the container-explain. [AP 15, 18]
Answer:
The pressure of an ideal gas in container = \(\frac{1}{3}nm\overline{\mathrm{v}}^2\)

This pressure is independent of area A. By Pascal’s law, pressure in one portion of the gas in equilibrium is the same as any where else. Hence pressure of an ideal gas in container is independent of shape of the container.

Question 8.
Explain the concept of degrees of freedom for molecules of a gas.
Answer:
The total number of possible independent ways in which the particles of a system can take up energy is called the degree of freedom of that system.

A molecule free to move in space has three translational degrees of freedom.
Each atom of a monoatomic gas has only three translational degrees of freedom.
A diatomic molecule has 5 degrees of freedom(3 translational and 2 rotational).

Question 9.
What is the expression between pressure and kinetic energy of a gas molecule? [AP 15, 16, 17]
Answer:

Thus, the pressure exerted by a gas is numerically equal to 2/3rd of the kinetic energy of the molecules present per unit volume of the gas.

Question 10.
The absolute temperature of a gas is increased 3 times. What will be the increase in rms velocity of the gas molecule? [AP ,19][TS 15,19,20]
Answer:

Short Answer Questions

Question 1.
Explain the kinetic interpretation of Temperature.
Answer:
The average kinetic energy of a molecule is \(\frac{1}{2}m\overline{\mathrm{v}}^2=\frac{3}{2}\)K_BT

It is clear from above equation that the mean kinetic energy of a molecule is directly propor¬tional to the absolute temperature of the gas. It is independent of pressure, volume (or) the nature of the ideal gas., when the temperature of the gas is increased, the mean kinetic energy of the molecule increases. On the other hand, why heat is withdrawn from a gas, the mean kinetic energy of the molecules decreases. Thus, the temperature of a gas is a measure of the mean translational kinetic energy per molecule of the gas. This is known as ‘kinetic interpretation of temperature’.

Question 2.
How specific heat capacity of mono-atomic, diatomic and poly-atomic gases can be explained on the basis of Law of equipartition of Energy? [AP, TS I6]
Answer:
Law of Equipartition of Energy:
Statement :
“According to law of equipartition of energy, each translational and rotational degree of freedom of molecule contributes \(\frac{1}{2}\)K_BT to its energy.” [TS 18]

Monoatomic gas :
A monoatomic gas molecule has three degrees of freedom energy associated

Diatomic gas :
A diatomic gas molecule has five degrees of freedom. Total internal energy

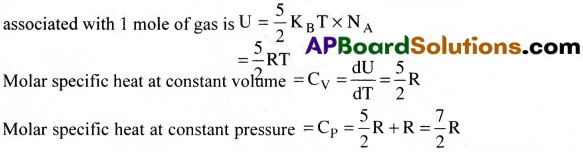
Polyatomic gas :
A polyatomic molecule has 3 translational, 3 rotational degrees of freedom and atleast one (or) more number (f) of vibrational modes.
The internal energy associated with 1 mole of gas

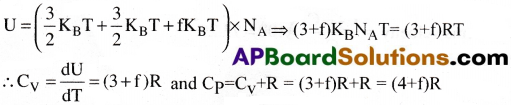
Question 3.
Explain the concept of absolute zero of temperature on the basis of kinetic theory.
Answer:
The average kinetic energy of a molecule.

When T=0 K then Vrms = 0. This leads us to the following definition of absolute zero of temperature. Absolute zero of temperature may be defined as that temperature at which the velocities of the gas molecules becomes zero.

In other words all molecular motion ceases at absolute zero of temperature. This definition is true only in the case of an ideal gas. The value of absolute zero for an ideal gas is -273.15°C. Before the absolute zero of temperature is reached all the gases change their state to liquids and then to solids.

Question 4.
Prove that the average kinetic energy of a molecule of an ideal gas is directly proportional to the absolute temperature of the gas.
Answer:
The pressure exerted by the gas is given by P = \(\frac{1}{3}nm\overline{\mathrm{v}}^2\) ……….. (1)
Where n=number of molecules per unit volume of the sample n = \(\frac{N}{V}\)
\(\overline{\mathrm{V}}^2\) = mean of the squared speed.
Equ. (1) can also be written as

∴ Average kinetic energy of a molecule is directly proportional to absolute temperature of the gas.

Question 5.
Two thermally insulated vessels 1 and 2 of volumes V₁ and V₂ are joined with a valve and tilled with air at temperatures (T₁, T₂) and pressure (P₁P₂) respectively. If the valve joining the two vessels is opened. What will be the temperature inside the vessels at equilibrium.
Answer:

Question 6.
What is the ratio of r.m.s speed of Oxygen & Hydrogen molecules at the same temperature?
Answer:

Question 7.
Four molecules of a gas have speeds 1, 2, 3 and 4 km/s. Find the rms speed of the gas molecule.
Answer:

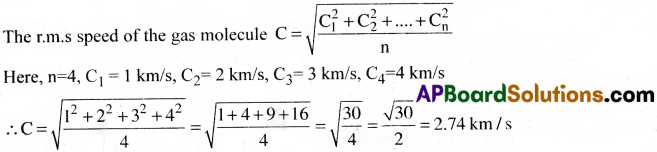
Question 8.
If h gas has ‘f’ degrees of freedom, find the ratio of C_p and C_v.
Answer:
According to law of equipartition of energy each translational and rotational degree of freedom of a molecule, contributes \(\frac{1}{2}\)K_BT to its energy.
Let a polyatomic molecule have ‘f’ degrees of freedom.
Energy associated with 1 mole of polyatomic gas is U = \(\frac{f}{2}\)K_BT × N_A
where N_A = Avogadro’s number
⇒ U = \(\frac{1}{2}\)RT[∵ R = N_AK_B]

Question 9.
Calculate the molecular K.E of I gram of Helium (Molecular weight 4) at 127°C. Given R = 8.31 J mol^-1 K^-1.
Answer:
Molecular kinetic energy of 1 gram of Helium = \(\frac{3}{2}\frac{RT}{M}\)
Here R = 8.31 Jmol^-1 K^-1, T = 273 + 127 = 400K and M = 4

Question 10.
When pressure increases by 2%, what is the percentage decrease in the volume of a gas, assuming Boyle’s law is obeyed?
Answer:
According to Boyle’s law, PV = constant

Long Answer Questions

Question 1.
Derive an expression for the pressure of an ideal gas in a container from Kinetic theory and hence give kinetic interpretation of temperature.
Answer:

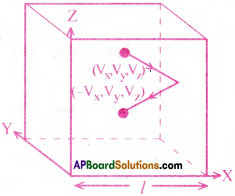
Consider a gas is enclosed in a cube of side ‘l’.
Let the axes be parallel to the sides of the cube as shown in fig.
A molecule with velocity (V_x,V_y,V_z) hits the wall which is parallel to YZ plane of area A(=l²). Since the collision is elastic the molecule rebounds with the same velocity. The velocity of molecule after collision is (-V_x,V_y,V_z).
The change in momentum of the molecule = -mV_x-(+mV_x) = -2mV_x.

According to principle of conservation of momentum, the momentum imparted to the wall in the collision = -(-2mV_x) = 2mV_x
The number of molecules with velocity (V_x,V_y,V_z) hitting the wall in time ∆t is \(\frac{1}{2}\) AV_x ∆tn
Where ‘h’ is the number of molecules per unit volume.
The total momentum transferred to the wall by the molecules = Q = (2mV_x) × \(\frac{1}{2}\) AV_x ∆tn

Kinetic interpretation of Temperature:
The average kinetic energy of a molecule is \(\frac{1}{2}m\overline{\mathrm{v}}^2\) = \(\frac{3}{2}\)K_BT

It is clear from above equation that the mean kinetic energy of a molecule is directly proportional to the absolute temperature of the gas. It is independent of pressure, volume (or) the nature of the ideal gas., Why the temperature of the gas is increased, the mean kinetic energy of the molecule increases. On the other hand, why heat is withdrawn from a gas, the mean kinetic energy of the molecules decreases. Thus, the temperature of a gas is a measure of the mean translations kinetic energy per molecule of the gas. This is known as ’kinetic interpretation of temperature’.

Exercise Problems

Question 1.
Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be 3A”.
Solution:
Considering spherical shape of molecule,
Volume of oxygen molecule = \(\frac{4}{3}\)πr³ = \(\frac{4}{3}\) × 3.14(\(\frac{3}{2}\) × 10^-10)³ = 4.13 × 10^-30 m³
Volume of 6.023 × 10²³ molecules =14.13 × 10^-30 × 6.023 × 10²³
= 85.11 × 10^-7 m³ = 8.511 × 10^-6m³ = 8.511 × 10^-3 litre
Molecular volume of one mole of oxygen = 8.511 × 10^-3 litre
Actual volume occupied by one mole of oxygen at STP = 22.4 litre
Fraction of molecular volume to actual volume = \(\frac{8.511\times10^{-3}}{22.4}\) = 3.8 × 10^-4 ≈ 4 × 10^-4

Question 2.
Molar volumes the volume occupied by 1° mole of any (ideal) gas-at standard temperature and pressure. Show that it is 22.4 litres.
Solution:

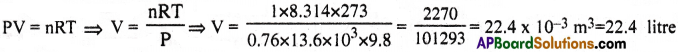
Question 3.
Estimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity 25.0 m3 at a temperature of 27°C and 1 atm pressure.
Solution:
PV = nRT (or) PV = nN_AK_BT (or) PV = N_tK_BT
Here N_t represents the total number of air molecules in the given gas

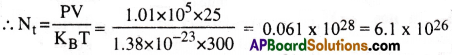
Question 4.
Estimate the average thermal energy of a helium atom at
(i) room temperature (27°C)
(ii) the temperature on the surface of the sun (6000K)
(iii) the temperature of 10 million kelvin
Solution:
(i) T = 27 + 273 = 300K

Multiple Choice Questions

Question 1.
The number of translational degrees of freedom tor a diatomic gas is
1) 2
2) 3
3) 5
4) 6
Answer:
2) 3

Question 2.
The degrees of freedom of a triatomic gas is
1) 6
2) 4
3) 2
4) 8
Answer:
1) 6

Question 3.
To find out degree of freedom, the expression is :

Answer:
1

Question 4.
A polyatomic gas with n degrees of freedom has a mean energy per molecule given by

Answer:
3

Question 5.
The average thermal energy for a mono-atomic gas is (k(i is Boltzmann constant and T, absolute temperature)

Answer:
2

Question 6.
A gas mixture consists of 2 moles of O₂ and 4 moles of Ar at temperature T. Neglecting all vibrational modes, the total internal energy of the system is
1) 15 RT
2) 9 RT
3) 11 RT
4) 4 RT
Answer:
3) 11 RT

Question 7.
The molar specific heat at constant pressure of an ideal gas is (7/2)R. The ratio of specific heat at constant pressure to that at constant volume is
1) 9/7
2) 7/5
3) 8/7
4) 5/7
Answer:
2) 7/5

Question 8.
The value of γ(=\(\frac{C_p}{C_v}\)), for hydrogen, helium and another ideal diatomic gas X (whose molecules are not rigid but have an additional vibrational mode), are respectively equal to
1) 7/5, 5/3, 9/7
2) 5/3, 7/5, 9/7
3) 5/3, 7/5, 7/5
4) 7/5, 5/3, 7/5
Answer:
1) 7/5, 5/3, 9/7

Question 9.
For a certain gas the ratio of specific heats is given to be γ = 1.5. For this gas
1) C_v = 3R/J
2) C_p = 3R/J
3) C_p = 5R/J
4) C_v = 5R/J
Answer:
2) C_p = 3R/J

Question 10.
For hydrogen gas C_p – C_v = a and for oxygen gas C_p – C_v = b, so the relation between a and b is given by
1) a = 16b
2) 16b = a
3) a = 4b
4) a = b
Answer:
4) a = b

Question 11.
For a certain gas, \(\frac{R}{C_v}\) = 0.67 up of molecules which are
1) diatomic
2) mixture of diatomic and polyatomic molecules
3) monoatomic
4) polyatomic.
Answer:
3) monoatomic

Question 12.
Relation between pressure (P) and kinetic energy per unit volume (E) of a gas is
1) P = \(\frac{2}{3}\)E
2) P = \(\frac{1}{3}\)E
3) P = E
4) P = 3E
Answer:
1) P = \(\frac{2}{3}\)E

Question 13.
In a vessel, the gas is at pressure P. If the mass of all the molecules is halved and their speed is doubled, then the resultant pressure will be
1) 2P
2) P
3) P/2
4) 4P
Answer:
1) 2P

Question 14.
e containers of the same volume contain three different gases. The masses es of the molecules are m₁, m₂ and m₃ and the number of molecules in their resp active containers are N₁, N₂ and N₃. These gas pressure in the containers are P₁, P₂ and P₃ respectively. All the gases are now mixed and put in one of these containers. The pressure P of the n fixture will be
1) P < (P₁ + P₂ + P₃)
2) P = \(\frac{P_1+P_2+P_3}{3}\)
3) P = P₁ + P₂ + P₃
4) P > (P₁ + P₂ + P₃)
Answer:
3) P = P₁ + P₂ + P₃

Question 15.
The equation of state for 5g of oxygen at a pressure P and temperature T, when occupying a volume V, will be (Where R is constant)
1) PV = (5/32) RT
2) PV = 5RT
3) PV = (5/2) RT
4) PV = (5/16) RT
Answer:
1) PV = (5/32) RT

Question 16.
The molecules of a given mass of a gas have r.m.s. velocity of 200 ms-1 to at 27°C and 1.0 × 10⁵ Nm^-2 pressure. When the temperature and pressure of the gas are respectively, 127°C and 0.05 × 10⁵ N m^-2, the r.m.s. velocity of its molecules in m s^-1 is

Answer:
4

Question 17.
Two containers A and B are partly tilled with water and closed. The volume of A is twice that of B and it contains half the amount of water in B. If both are at the same temperature, the water vapour in the containers will have pressure in the ratio of
1) 1 : 2
2) 1 : 1
3) 2 : 1
4) 4 : 1
Answer:
2) 1 : 1

Question 18.
At 10°C the value of the density of a fixed mass of an ideal gas divided by its pressure is x. At 110°C this ratio is
1) 10/110 x
2) 283/383 x
3) x
4) 383/283x
Answer:
2) 283/383 x

Question 19.
The value of critical temperature in terms of vander Waals’ constant a and b is given by

Answer:
1

Question 20.
The mean free path for a gas, with molecular diameter d and number density n can be expressed as

Answer:
2

Question 21.
The mean free path of molecules of a gas, (radius r) is inversely proportional to
1) r³
2) r²
3) r
4) √r
Answer:
2) r²

Question 22.
At constant volume, temperature is increased then
1) collision on walls will be less
2) number of collisions per unit time will increase
3) collisions will be in straight lines
4) collisions will not change.
Answer:
2) number of collisions per unit time will increase

Question 23.
At 0 K which of the following properties of a gas will be zero?
1) vibrational energy
2) density
3) kinetic energy
4) potential energy
Answer:
3) kinetic energy

Question 24.
According to kinetic theory of gases, at absolute zero of temperature
1) water freezes
2) liquid helium freezes
3) molecular motion stops
4) liquid hydrogen freezes.
Answer:
3) molecular motion stops

Question 25.
Increase in temperature of a gas filled in a container would lead to
1) decrease in intermolecular distance
2) increase in its mass
3) increase in its kinetic energy
4) decrease in its pressure
Answer:
3) increase in its kinetic energy