TS Inter 2nd Year Physics Question Paper March 2020

Thoroughly analyzing TS Inter 2nd Year Physics Model Papers and TS Inter 2nd Year Physics Question Paper March 2020 helps students identify their strengths and weaknesses.

TS Inter 2nd Year Physics Question Paper March 2020

Time: 3 Hours
Maximum Marks: 60

Section – A (10 × 2 = 20)

Note :

• Answer all questions.
• Each question carries two marks.
• All are Very Short Answer Type Questions.

Question 1.
What are cathode rays ?
Answer:
Cathode rays are streams of fast moving electrons or negatively charged particles.

Question 2.
State Heisenberg’s Uncertainty Principle.
Answer:
Uncertainity principle states that “it is impossible to measure both position (ΔX) and momentum of an electron (ΔP) [or any other particle] at the same time exactly”, i.e., ΔX . Δp ≈ h where ΔX is uncertainty in the specification of position and Δp is uncertainty in the specification of position and Δp is uncertainty in the specification of momentum.

Question 3.
Which gates are called Universal Gates ?
Answer:
NAND gate and NOR gates are called universal gates.

Question 4.
Which type of communication is employed in mobile phones ?
Answer:
Space wave mode of propagation is employed in mobile phones.

Question 5.
What is the magnetic moment associated with a solenoid ?
Answer:
Magnetic dipole moment is a solenoid m = NIA
Where ‘N’ is the number of turns in the loop, ‘I’ the current and A the area vector.

Question 6.
A concave mirror produces an image of a long vertical pin placed 40 cm from the mirror at the position of the object. Find the focal length of the mirror.
Solution:
Given u = υ = 40cm
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{\mathrm{υ}}\) + \(\frac{1}{U}\)
\(\frac{1}{\mathrm{f}}\) = \(\frac{1}{40}\) + \(\frac{1}{40}\)
\(\frac{1}{\mathrm{f}}\) = \(\frac{2}{40}\)
f = 20 cm.

Question 7.
Define magnetic declination.
Answer:
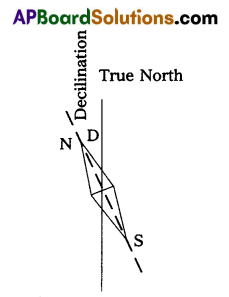
Magnetic Declination (D) : The angle between the true geographic north and the north shown by a compass needle is called magnetic declination or simply declination (D).]

Question 8.
Distinguish between ammeter and voltmeter.
Answer:

Ammeter	Voltmeter
1) It is used to measure ‘ current.	1) It is used to measure RD between two points.
2) Resistance of an ideal Ammeter is zero.	2) Resistance of ideal voltmeter is infinity.
3) It is connected in series in the circuits.	3) It is connected in parallel in the circuits.

Question 9.
A power transmission line feeds input power at 2300 V to a stepdown transformer with its primary windings having 4000 turns. What should be the number of turns in the secondary in order to get output power at 230 V ?
Solution:
Given Primary voltage V_p = 2300V
N_p = 4000 turns
Secondary voltage V_s = 230V.
Using formula,
\(\frac{\mathrm{V}_{\mathrm{S}}}{\mathrm{V}_{\mathrm{p}}}=\frac{\mathrm{N}_{\mathrm{s}}}{\mathrm{N}_{\mathrm{p}}}\)
\(\frac{230}{2300}\) = \(\frac{N_2}{4000}\)
N_s = 400
∴ Thus, the number of turns in secondary are 400.

Question 10.
What are the applications of microwaves ?
Answer:

1. Microwaves are used in Radars.
2. Microwaves are used for cooking purposes.
3. A radar using microwave can help in detecting the speed of automobile while in motion.

Section – B (6 × 4 = 24)

Note :

• Answer any six of the following questions.
• Each question carries four marks.
• All are Short Answer Type Questions.

Quetsion 11.
Explain the formation of a rainbow.
Answer:

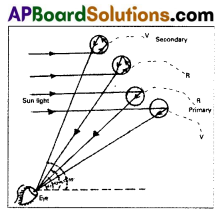
Figure shows how sunlight is broken into its segments in the process and a rainbow appears. The dispersion of the violet and the red rays after internal reflection in the drop is shown in figure.

The red rays emerge from the drops of water at one angle (43°) and the violet rays emerge at another angle (41°). The large number of water drops in the sky makes a rainbow. The rainbow appears semicircular for an observer on earth.

Question 12.
How do you determine the resolving power of your eye ?
Answer:
Make black strips of equal width separated by white strips. All the black strips having same width, while he width of white strips should increase from left to right.

Now watch the pattern with one eye. By moving away (or) closer to the wall, find the position where you can just see some two black strips as separate strips.

All black strips to the left of this strips would merge into one another and would not be distinguishable on the other hand, the black strips to the right of this would be more and more clearly visible.

Note the width d of the white strips and measure the distance D of the wall from eye.
Then resolution of your eye = \(\frac{d}{D}\)

Question 13.
Derive an expression for the intensity of the electric field at a point on the equatorial plane of an electric dipole.
Answer:
Electric field intensity on equitorial line of electric dipole:

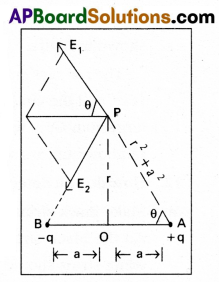
• Consider an electric dipole consisting of two charges – q and +q separated by a distance ‘2a’ with centre at ‘O’.
• We shall calculate electric field E at P on equitorial line of dipole and at a distance OP = r.
• Let E₁ and E₂ be the electric fields at P due to charges +q and – q respectively.
• The ⊥^r components (E₁ sin θ and E₂ sin θ) cancel each other, because they are equal and opposite. The II^el components (E₁ cos θ and E₂ cos θ) are in the same direction and hence add up.
• The resultant field intensity at point P is given by E = E₁ cos θ + E₂ cos θ

• From figure, cos θ = \(\frac{a}{\left(r^2+a^2\right)^{1 / 2}}\)
  ∴ E = \(\frac{1}{4 \pi \varepsilon_0}\) × \(\frac{2 a q}{\left(r^2+a^2\right)^{3 / 2}}\)
• If r > > a, then a² can be neglected in comparison to r². Then
  E = \(\frac{P}{4 \pi \varepsilon_0}\) × \(\frac{1}{\mathrm{r}^3}\)
  In vector form \(\vec{E}=\frac{\vec{P}}{4 \pi \varepsilon_0 r^3}\)

Question 14.
Derive an expression for the capacitance of a parallel plate capacitor.
Answer:
Expression for the capacitance of a parallel plate capacitor :

• P and Q are two parallel plates of a capacitor separated by a distance of d.
• The area of each plate is A. The plate P is charged and Q is earth connected.
• The charge on Pis +q and surface charge density of charge = o
  ∴ q = Aσ
• The electric intensity at point
  x, E = \(\frac{|\sigma|}{\varepsilon_0}\)

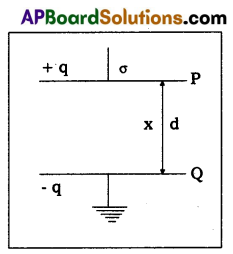
• Potential difference between the plates P and Q.
  V = \(\int \mathrm{dV}=\int_{\mathrm{d}}^0-\mathrm{Edx}=\int_{\mathrm{d}}^0 \frac{-\sigma}{\varepsilon_0} \mathrm{dx}=\frac{\sigma \mathrm{d}}{\varepsilon_0}\)
• Capacitance of the capacitor C = \(\frac{Q}{V}=\frac{A \sigma}{\frac{\sigma d}{\varepsilon_0}}=\frac{\varepsilon_0 A}{d}\) Farads (In air)
  Note : Capacity of a capacitor with dielectric medium is
  C = \(\frac{\varepsilon_0 A}{\left[d-t+\frac{t}{k}\right]}\) Farads.

Question 15.
State and explain Biot – Savart Law.
Answer:
Consider a very small element of length dl of a conductor carrying current (i). Magnetic induction due to small element at a point P distance r from the element.
Magnetic induction (dB) is directly proportional to i) current (ii) Length of the element (dl) iii) sine angle between r and dl and iv) Inversely proportional to the square of the distance from small element to point P.
dB ∞ = \(\frac{\mathrm{id} 1 \sin \theta}{\mathrm{r}^2}\)
dB = \(\frac{\mu_0}{4 \pi}\) . \(\frac{\mathrm{id} 1 \sin \theta}{\mathrm{r}^2}\)
where µ₀ = permeability in free space.
\(\frac{\mu_0}{4 \pi}\) = 10^-7 Wb m^-1 A^-1
In vector form \(\overline{\mathrm{dB}}=\frac{\mu_0 \mathrm{i}}{4 \pi} \frac{(\overline{\mathrm{d} \ell} \times \overrightarrow{\mathrm{r}})}{\mathrm{r}^3}\)

Question 16.
Obtain an expression for the magnetic energy stored in a solenoid in terms of magnetic field B, area A and length of the solenoid.
Answer:

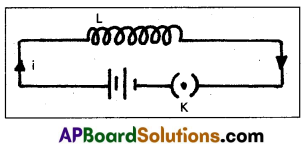
When the current flows through the inductor of inductance L, an e.m.f is induced in it is given by
ε = -L\(\frac{\mathrm{dI}}{\mathrm{dt}}\) ………… (1)
(-ve sign shows that e.m.f opposes the passage of current)
Let an infinitesmal charge dq be driven through the inductor. So the work done by the external voltage is given by

Question 17.
What are the limitations of Bohr’s theory of hydrogen atom ?
Answer:
Limitations of Bohr’s theory of Hydrogen atom :

1. This theory is applicable only to simplest atom like hydrogen, with z = 1. The theory fails incase of atoms of other elements for which z > 1.
2. The theory does not explain why orbits of electrons are taken as circular, while elliptical orbits are also possible.
3. Bohr’s theory does not say anything about the relative intensities of spectral lines.
4. Bohr’s theory does not take into account the wave properties of electrons.

Question 18.
Distinguish between half – wave and full – wave rectifiers.
Answer:

Half wave rectifier	Full wave rectifier
1) Single diode is used.	1) Two diodes are used.
2) Only half wave is rectified	2) Full wave is rectified
3) Rectifier efficiency η = \(\frac{0.406 \mathrm{R}_{\mathrm{L}}}{\mathrm{r}_{\mathrm{f}}+\mathrm{R}_{\mathrm{L}}}\)	3) Rectifier efficiency η = \(\frac{0.812 R_L}{r_f+R_L}\)
4) Efficiency of half wave rectifier is 40.6%.	4) Efficiency of full wave rec-tifier is 81.2%.
5) Output is discontinuous and pulsative.	5) Output is continuous and pulsative.

Section – C (2 × 8 = 16)

Note :

• Answer any two of the following questions.
• Each question carries eight marks.
• All are Long Answer Type Questions.

Question 19.
Explain the formation of stationary waves in an air column enclosed in open pipe. Derive the equations for the frequencies of the harmonics produced.
An open organ pipe 30 cm long is sounded. If the velocity of sound is 330 m/s, what is the fundamental frequency of vibration of the air column ?
Answer:
A pipe, which is opened at both ends is called open pipe. When a sound wave is sent through a open pipe, which gets reflected by the earth. Then incident and reflected waves are in same frequency, travelling in the opposite directions are superimposed stationary waves are formed.

Harmonics in open pipe : To form the stationary wave in open pipe, which has two anti nodes at two ends of the pipe with a node between them.
∴ The vibrating length (l)
= half of the wavelength \(\frac{\lambda_1}{2}\) ⇒ λ₁ = 2l
l = \(\frac{\lambda_1}{2}\) ⇒ λ₁ = 2l

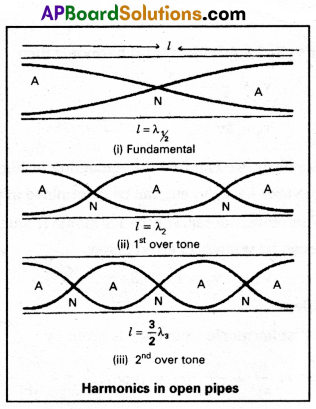
fundamental frequency v₁ = \(\frac{v}{\lambda_1}\) where v is velocity of sound in air v₁ = \(\frac{v}{2 l}\) …………. (1)
For second harmonic (first overtone will have one more node and antinode than the fundamental.

If λ₂ is wavelength of second harmonic l = \(\frac{2 \lambda_2}{2}\) ⇒ λ₂ = \(\frac{2 l}{2}\)
If ‘v₂‘ is frequency of second harmonic then
v₂ = \(\frac{v}{\lambda_2}\) = \(\frac{\vartheta \times 2}{21}\) = 2v
v₂ = 2V ………… (2)

Similarly, for third harmonic (second overtone) will have three nodes and four antinodes as shown in above figure.
If λ₃ is wavelength of third harmonic l = \(\frac{2 \ell}{2}\)
λ₃ = \(\frac{2 \ell}{2}\)
If ‘v₂‘ is frequency of third harmonic then
v₃ = \(\frac{υ}{\lambda_3}\) = \(\frac{υ \times 3}{21}\) = 3v
v₃ = 3v ………… (3)

Similarly, we can find the remaining or higher harmonic frequencies i.e, v₃, v₄ etc, can be determined in the same way.
Therefore, the ratio of the harmonic frequencies in open pipe can be written as given below,
v : v₁ : v₂ = 1 : 2 : 3

Problem:
The first harmonic frequency is given by
v¹ = \(\frac{υ}{\lambda_1}\) = \(\frac{υ}{2 L}\) (oPen PiPe)
Where L is the length of the pipe. The frequency of its n^th harmonic is
vⁿ = \(\frac{\mathrm{nυ}}{2 \mathrm{~L}}\) for n = 1, 2, 3, (open pipe)
First few modes of an open pipe are shown in Fig.
For L = 30.0 cm. υ = 330 m s^-1
vⁿ = \(\frac{\mathrm{n} \times 330\left(\mathrm{~m} \mathrm{~s}^{-1}\right)}{0.6(\mathrm{~m})}\) = 550 s^-1

Clearly, for a source of frequency 1.1 kHz the air column will resonate at υ₂, i.e., the second harmonic.
Now, if one end of the pipe is closed (Fig.), the fundamental frequency is
v₁ = \(\frac{υ}{\lambda_1}\) = \(\frac{υ}{2 L}\) (pipe closed at one end)

and only to odd numbered harmonics are present :
v₃ = \(\frac{3 υ}{4 L}\), v₅ = \(\frac{5 υ}{4 L}\) ’ and s0 on.
For L = 30 cm and υ = 330 m s^-1, the fundamental frequency of the pipe closed at one end is 275 Hz and the source frequency corresponds to its fourth harmonic. Since, this harmonic is not a possible mode, no resonance will be observed with the source, the moment one end is closed.

Question 20.
State the working principle of potentiometer. Explain with the help of a circuit diagram, how the potentiometer is used to determine the internal resistance of the given primary cell.
In a potentiometer arrangement, a cell of emf 1.25 V gives a balance point at 35.0 cm length of the wire. If the cell is replaced by another cell and the balance point shifts to 63.0 cm, what is the emf of the second cell ?
Answer:
Working principle of potentiometer: The potential difference across a length of the potentiometer wire is directly propotional to its length (or) when a steady current is passed through a uniform wire, potential drop per unit length or potential gradient is constant.
i.e., ε α l ⇒ ε = Φl where Φ is potential gradient.

Measurement of internal resistance (r) with potentiometer :

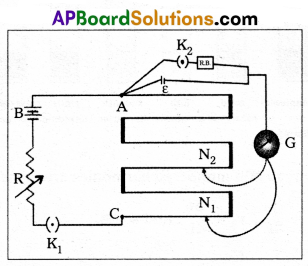
• Potentiometer to measure internal resistance (r) of a cell (ε) is shown in diagram
• The cell (emf ε) whose internal resistance box (R.B) through a key K₂.
• With key K₂ open, balance is obtained at length l₁(AN₁).
  Then ε = Φl₁ ………….. (1)
• When key K₂ is closed, the cell sends a current (I) through the resistance box (R.B).
• If V is the terminal potential difference of the cell and balance is obtained at length l2 (AN₂)
  Then V = Φl₂ → (2)
• \(\frac{(1)}{(2)}\) ⇒ \(\frac{\varepsilon}{V}\) = \(\frac{l_1}{l_2}\) → (3)
• But, ε = I(r + R) and V = IR. This gives
  \(\frac{\varepsilon}{\mathrm{V}}\) = \(\frac{(\mathrm{r}+\mathrm{R})}{\mathrm{R}}\)
  \(\frac{l_1}{l_2}\) = (\(\frac{r}{R}\) + 1) [Q from (3)]
  ∴ r = R(\(\frac{l_1}{l_2}\) – 1)

Problem :
Here ε₁ = 1.25 V, l₁ = 35.0 cm, ε₂ = ?. l₂ = 63.0 cm.
AS \(\frac{\varepsilon_2}{\varepsilon_1}=\frac{l_2}{l_1}\) or
ε₂ = \(\frac{\varepsilon_1 \times l_2}{l_1}\) = \(\frac{1.25 \times 63}{35}\) = 2.25 V

Question 21.
Explain the principle and working of a nuclear reactor with the help of a labelled diagram.
Answer:
Principle : A nuclear reactor works on the principle of achieving controlled chain reaction in natural Uranium ²³⁸U enriched with ²³⁵U, consequently generating large amounts of heat.

A nuclear reactor consists of
(1) Fuel
(2) Moderator
(3) Control rods
(4) Radiation shielding
(5) Coolant.

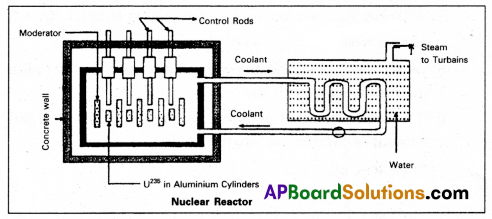
1. Fuel and clad : In reactor the nuclear fuel is fabricated in the form of thin and long cylindrical rods. These group of rods treated as a fuel assembly. These rods are surrounded by coolant, which is used to transfer of heat produced in them. A part of the nuclear reactor which use to store the nuclear fuel is called the core of the reactor. Natural uranium, enriched uranium, plutonium and uranium – 233 are used as nuclear fuels.

2. Moderator : The average energy of neutrons released in fission process is 2 MeV They are used to slow down the velocity of neutrons. Heavy water or graphite are used as moderating materials in reactor.

3. Control Rods : These are used to control the fission rate in reactor by absorbing the neutrons. Cadmium and boron are used as controlling the neutrons, in the form of rods.

4. Shielding : During fission reaction beta and gamma rays are emitted in addition to neutrons. Suitable shielding such as

steel, lead, concrete etc. are provided around the reactor to absorb and reduce the intensity of radiation to such low levels that do not harm the operating personnel.

5. Coolant : The heat generated in fuel elements is removed by using a suitable coolant to flow around them. The coolants used are water at high pressures, molten sodium etc.

Working : Uranium fuel rods are placed in the aluminium cylinders. The graphite moderator is placed in between the fuel cylinders. To control the number of neutrons, a number of control rods of cadmium or beryllium or boron are placed in the holes of graphite block. When a few ²³⁵U nuclei undergo fission fast neutrons are liberated. These neutrons pass through the surrounding graphite moderator and loose their energy to become thermal neutrons. These thermal neutrons are captured by ²³⁵U. The heat generated here is used for heating suitable coolants which in turn heat water and produce steam. This steam is made to rotate steam turbine and there by drive a generator of production for electric power.