TS Inter 2nd Year Maths 2A Question Paper May 2017

Thoroughly analyzing TS Inter 2nd Year Maths 2A Model Papers and TS Inter 2nd Year Maths 2A Question Paper May 2017 helps students identify their strengths and weaknesses.

TS Inter 2nd Year Maths 2A Question Paper May 2017

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three Sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer all the questions.
• Each question carries two marks.

Question 1.
Find the complex conjugate of (3 + 4i) (2 – 3i).
Solution:
Let Z = (3 + 4i) (2 – 3i)
= 6 – 9i + 8i – 12i²
= 6 – i – 12(-1)
= 6 – i + 12
= 18 – i
∴ \(\bar{Z}\) = 18 + i
∴ The complex conjugate of (3 + 4i) (2 – 3i) is 18 + i.

Question 2.
If the Arg \(\bar{Z}_1\) and Arg Z2 are \(\frac{\pi}{5}\) and \(\frac{\pi}{3}\) respectively then find Arg Z₁ + Arg Z₂.
Solution:

Question 3.
If 1, w, w² are the cube roots of unity, then prove that \(\frac{1}{2+w}+\frac{1}{1+2 w}=\frac{1}{1+w}\).
Solution:
Given 1, w, w² are the cube roots of unity.
∴ 1 + w + w² = 0 and w³ = 1

Question 4.
Find the value of m for the equation having equal roots x² – 15 – m(2x – 8) = 0.
Solution:
Given equation is x² – 15 – m(2x – 8) = 0
⇒ x² – 15 – 2mx + 8m = 0
⇒ x² – 2mx + 8m – 15 = 0
Since it has equal roots
∴ (-2m)² – 4(1)(8m – 15) = 0
⇒ 4m² – 32m + 60 = 0
⇒ m² – 8m + 15 = 0
⇒ m² – 3m – 5m + 15 = 0
⇒ m(m – 3) – 5(m – 3) = 0
⇒ (m – 3) (m – 5) = 0
⇒ m = 3, 5

Question 5.
If α, β, 1 are the roots of x³ – 2x² – 5x + 6 = 0, then find α, β.
Solution:
Given α, β, 1 are the roots of x³ – 2x² – 5x + 6 = 0
∴ Sum of the roots = \(\frac{-(-2)}{1}\)
⇒ α + β + 1 = 2
⇒ α + β = 1 ………(1)
Product of the roots = \(\frac{-(6)}{1}\)
⇒ α . β . 1 = -6
∴ (α – β)² = (α + β)² – 4αβ
= 12 – 4(-6)
= 1 + 24
= 25
⇒ α – β = 5 ………(2)
(1) + (2) ⇒ 2α = 6
⇒ α = 3
From (1), 3 + β = 1
⇒ β = -2
∴ α = 3, β = -2

Question 6.
Find the number of terms in the expansion of (2x + 3y + z)⁷.
Solution:
The number of terms in the expansion of (2x + 3y + z)⁷ = \(\frac{(7+1)(7+2)}{2}\) = 36

Question 7.
Find the mean deviation about the mean for data 3, 6, 10, 4, 9, 10.
Solution:
The arithmetic mean of the given data is
\(\bar{x}=\frac{3+6+10+4+9+10}{6}\)
= \(\frac{42}{6}\)
= 7
The absolute values of the deviations are |3 – 7|, |6 – 7|, |10 – 7|, |4 – 7|, |9 – 7|, |10 – 7| = 1, 1, 3, 3, 2, 3
∴ The mean deviation from the mean = \(\frac{4+1+3+3+2+3}{6}\)
= \(\frac{16}{6}\)
= 2.666

Question 8.
Find the number of injections of set A with 5 elements to set B with 7 elements.
Solution:
Here n(A) = 5 and n(B) = 7
∴ The number of injections of set A to a set B is \(n(B)_{p_n(A)}={ }^7 p_5\)
= 7 × 6 × 5 × 4 × 3
= 2,520

Question 9.
If ⁹C₃ + ⁹C₄ = ¹⁰C_r then find r.
Solution:
Given ⁹C₃ + ⁹C₄ = ¹⁰C_r
we know ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r
∴ ¹⁰C₄ = ¹⁰C_r
⇒ r = 4 (or) 10 = 4 + r
⇒ r = 4 (or) r = 6

Question 10.
If the mean and variance of a binomial variable x are 2.4 and 1.44, then find n.
Solution:
Let X follow a binomial distribution with parameters n and p.
∴ Mean np = 2.4 and variance npq = 1.44
\(\frac{\mathrm{npq}}{\mathrm{np}}=\frac{1.44}{2.4}\)
⇒ q = 0.6
∴ p = 1 – q
= 1 – 0.6
= 0.4
∴ np = 2.4
⇒ n(0.4) = 2.4
⇒ n = 6

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Attempt any five questions.
• Each question carries four marks.

Question 11.
Show that the four points in the Argand plane represented by the complex numbers 2 + i, 4 + 3i, 2 + 5i, and 3i are the vertices of a square.
Solution:
Let A, B, C, and D be the points in the Argand plane.
∴ A = (2, 1), B = (4, 3), C = (2, 5), D = (0, 3)

∴ AB = BC = CD = DA and AC = BD.
∴ A, B, C, D are the vertices of a square.

Question 12.
Determine the range of the expression \(\frac{x^2+x+1}{x^2-x+1}\).
Solution:
Let y = \(\frac{x^2+x+1}{x^2-x+1}\)
⇒ x²y – xy + y = x² + x + 1
⇒ (y – 1)x² – x(y + 1) + y – 1 = 0
x is real ⇒ b² – 4ac ≥ 0
⇒ [-(y + 1)]² – 4(y – 1) (y – 1) ≥ 0
⇒ (y + 1)² – 4(y – 1)² ≥ 0
⇒ y² + 2y + 1 – 4(y² – 2y + 1) ≥ 0
⇒ y² + 2y + 1 – 4y² + 8y – 4 ≥ 0
⇒ -3y² + 10y – 3 ≥ 0
⇒ 3y² – 10y + 3 ≤ 0
⇒ 3y² – 9y – y + 3 ≤ 0
⇒ 3y(y – 3) – 1(y – 3) ≤ 0
⇒ (3y – 1) (y – 3) ≤ 0
⇒ y ∈ [\(\frac{-1}{3}\), 3]
∴ The range of y is [\(\frac{-1}{3}\), 3]

Question 13.
Resolve \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}\) into partial fractions,
Solution:
x⁴ + x² + 1 = x⁴ + 2x² + 1 – x²
= (x² + 1)² – x²
= (x² + 1 + x) (x² + 1 – x)
= (x² + x + 1) (x² – x + 1)
Let \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}=\frac{A x+B}{\dot{x}^2+x+1}+\frac{C x+D}{x^2-x+1}\)
⇒ 3x³ – 2x² – 1 = (Ax + B) (x² – x + 1) + (Cx + D) (x² + x + 1)
Equating the coefficients of like terms, we have
A + C = 3 ……..(1)
⇒ C = 3 – A
-A + B + C + D = -2 …….(2)
A – B + C + D = 0 ……….(3)
B + D = -1 ………(4)
⇒ D = -1 – B
Substitute C, D in (2)
-A + B + 3 – A – 1 – B = -2
⇒ -2A = -4
⇒ A = 2
∴ C = 3 – 2
⇒ C = 1
Substitute C, D in (3)
A – B + 3 – A – 1 – B = 0
⇒ -2B = -2
⇒ B = 1
∴ D = -1 – 1
⇒ D = -2
∴ A = 2, B = 1, C = 1, D = -2
∴ \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}=\frac{2 x+1}{x^2+x+1}+\frac{x-2}{x^2-x+1}\)

Question 14.
A, B, C are 3 newspapers from a city. 20% of the population read A, 16% read B, 14% read C, 8% both A and B, 5% both A and C, 4% both B and C and 2% all the three. Find the percentage of the population who read atleast one newspaper.
Solution:
Given P(A) = \(\frac{20}{100}\)
P(B) = \(\frac{16}{100}\)
P(C) = \(\frac{14}{100}\)
P(A ∩ B) = \(\frac{8}{100}\)
P(B ∩ C) = \(\frac{4}{100}\)
P(A ∩ C) = \(\frac{5}{100}\)
P(A ∩ B ∩ C) = \(\frac{2}{100}\)
We know P(A ∪ B ∪ C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(B ∩ C) – P(C ∩ A) + P(A ∩ B ∩ C)
= \(\frac{20}{100}+\frac{16}{100}+\frac{14}{100}-\frac{8}{100}-\frac{4}{100}-\frac{5}{100}+\frac{2}{100}\)
= \(\frac{35}{100}\)
∴ Percentage of population who read atleast one news paper = \(\frac{35}{100}\) × 100 = 35%.

Question 15.
Define conditional probability. State and prove the multiplication theorem of probability.
Solution:
Conditional Event: Suppose A and B are two events of a random experiment. If event B occurs after the occurrence of the event A. The event happening of B after the happening of A is called a conditional event and is denoted by \(\frac{B}{A}\).
Conditional Probability: If A and B are two events of a sample space S and P(A) ≠ 0 then the probability of B after the event A has occured is called the conditional probability given A and is denoted by P(\(\frac{B}{A}\)).
\(P\left(\frac{B}{A}\right)=\frac{P(B \cap A)}{P(A)}\), P(A) ≠ 0
Multiplication Theorem of Probability: If A and B are two events of a random experiment with P(A) > 0 and P(B) > 0 then P(A ∩ B) = P(A) P(\(\frac{B}{A}\)) = P(B) P(\(\frac{A}{B}\))
Proof: Let S be the sample space associated with the random experiment.
Let A and B be two events of S such that P(A) > 0 and P(B) > 0.
By the definition of conditional probability,
\(P\left(\frac{B}{A}\right)=\frac{P(B \cap A)}{P(A)}\)
∴ P(B ∩ A) = P(A) P(\(\frac{B}{A}\))
Since P(B) > 0, we interchange A and B in the above.
∴ P(A ∩ B) = P(B ∩ A) = P(B) P(\(\frac{A}{B}\))

Question 16.
If the letters of the word PRISON are permuted in all possible ways and the words thus formed are arranged in dictionary order, find the rank of the word PRISON.
Solution:
The letters of the given word in dictionary order are I, N, O, P, R, S
The number of words that begin with
I – – – – – = 5!
N – – – – – = 5!
O – – – – – = 5!
P I – – – – = 4!
P N – – – – = 4!
P O – – – – = 4!
P R I N – – = 2!
P R I O – – = 2!
P R I S N – = 1!
∴ The next word is P R I S O N = 1
The rank of the word PRISON = 3(5!) + 3(4!) + 2(2!) + 1! + 1
= 3(120) + 3(24) + 2(2) + 1 + 1
= 360 + 72 + 4 + 1 + 1
= 438

Question 17.
Simplify \({ }^{34} C_5+\sum_{r=0}^4{ }^{(38-r)} C_4\).
Solution:

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Attempt any five questions.
• Each question carries seven marks.

Question 18.
If n is a positive integer show that (1 + i)ⁿ + (1 – i)ⁿ = \(2^{\frac{n+2}{2}} \cos \left(\frac{n \pi}{4}\right)\).
Solution:

Question 19.
Solve the equation 2x⁵ + x⁴ – 12x³ – 12x² + x + 2 = 0.

Question 20.
If the coefficients of 4 consecutive terms in the expansion of (1 + x)ⁿ are a₁, a₂, a₃, a₄ respectively then show that \(\frac{a_1}{a_1+a_2}+\frac{a_3}{a_3+a_4}=\frac{2 a_2}{a_2+a_3}\).
Solution:
Given a₁, a₂, a₃, and a₄ are the coefficients of 4 consecutive terms in (1 + x)ⁿ respectively.

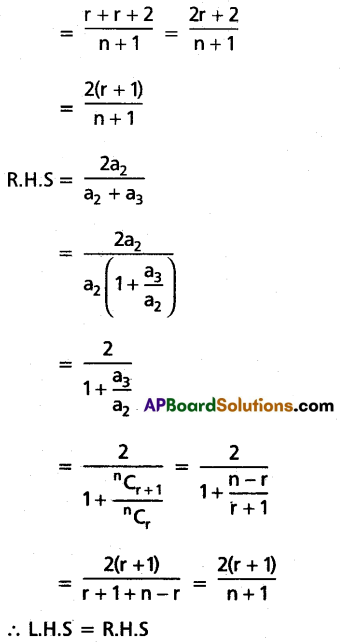
Question 21.
Find the sum of the infinite series \(1-\frac{4}{5}+\frac{4.7}{5.10}-\frac{4.7 .10}{5 \cdot 10.15}\) + ……….
Solution:

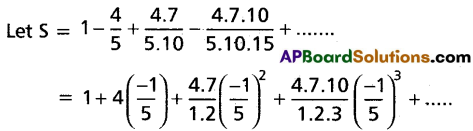
Question 22.
Find the mean deviation from the mean of the following data using the step deviation method:

Marks	0-10	10-20	20-30	30-40	40-50	50-60	60-70
Number of Students	6	5	8	15	7	6	3

Question 23.
Three Boxes B₁, B₂, and B₃ contain balls with different colours as shown below:

	White	Black	Red
B1	2	1	2
B2	3	2	4
B3	4	3	2

A die is thrown. B₁ is chosen if either 1 or 2 turns up. B₂ is chosen if 3 or 4 turns up and B₃ if 5 or 6 turns up. Having chosen a box in this way, a ball is chosen at random from this box, if the ball drawn is found to be red, find the probability that it is drawn from box B₂.
Solution:
Let E₁, E₂, E₃ be the events of choosing boxes B₁, B₂, and B₃ respectively.

Question 24.
The range of a random variable X is {0, 1, 2}. Given that P(X = 0) = 3C³, P(X = 1) = 4C – 10C², P(X = 2) = 5C – 1.
(i) Find the value of C.
(ii) P(X < 1), P(1 < X ≤ 2) and P(0 < X ≤ 3).
Solution:
Range or random variable X is {0, 1, 2}
(i) P(X = 0) + P(X = 1) + P(X = 2) = 1
⇒ 3C³ + 4C – 10C² + 5C – 1 = 1
⇒ 3C³ – 10C² + 9C – 2 = 0

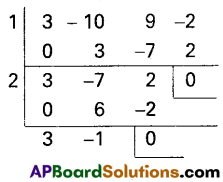
⇒ (C – 1) (3C² – 7C + 2) = 0
⇒ (C – 1) (C – 2) (3C – 1) = 0
⇒ C = 1 (or) 2 (or) \(\frac{1}{3}\)
If C = 1 (or) C = 2 then P(X = 0) > 1
∴ C ≠ 1 and C ≠ 2
(i) C = \(\frac{1}{3}\)
(ii) P(X < 1) = P(X = 0)
= 3C³
= \(3\left(\frac{1}{3}\right)^3\)
= 3(\(\frac{1}{27}\))
= \(\frac{1}{9}\)

(iii) P(1 < x ≤ 2) = P(X = 2)
= 5C – 1
= 5(\(\frac{1}{3}\)) – 1
= \(\frac{5-3}{3}\)
= \(\frac{2}{3}\)

(iv) P(0 < x ≤ 3) = P(X = 1) + P(X = 2)
= 4C – 10C² + 5C – 1
= -10C² + 9C – 1
= \(-10\left(\frac{1}{9}\right)+9\left(\frac{1}{3}\right)-1\)
= \(\frac{-10+27-9}{9}\)
= \(\frac{8}{9}\)