TS Inter 2nd Year Maths 2A Question Paper March 2018

Thoroughly analyzing TS Inter 2nd Year Maths 2A Model Papers and TS Inter 2nd Year Maths 2A Question Paper March 2018 helps students identify their strengths and weaknesses.

TS Inter 2nd Year Maths 2A Question Paper March 2018

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer all the questions.
• Each question carries two marks.

Question 1.
If z = 2 – 3i, then show that, z² – 4z + 13 = 0.
Solution:
Given z = 2 – 3i
⇒ (z – 2) = -3i
⇒ (z – 2)² = 9i²
⇒ z² – 4z + 4 = -9
⇒ z² – 4z + 13 = 0

Question 2.
If z₁ = -1 and z₂ = i, then find Arg(\(\frac{z_1}{z_2}\)).
Solution:
Given z₁ = -1
= -1 + i(0)
= cos π + i sin π
∴ Arg z₁ = π
Given z₂ = i
= 0 + i(1)
= cos \(\frac{\pi}{2}\) + i sin \(\frac{\pi}{2}\)
∴ Arg z₂ = \(\frac{\pi}{2}\)
Arg(\(\frac{z_1}{z_2}\)) = Arg z₁ – Arg z₂
= π – \(\frac{\pi}{2}\)
= \(\frac{\pi}{2}\)

Question 3.
If x = cis θ, then find the value of \(\left(x^6+\frac{1}{x^6}\right)\).
Solution:
Given x = cis θ = cos θ + i sin θ
⇒ x⁶ = (cos θ + i sin θ)⁶ = cos 6θ + i sin 6θ
\(\frac{1}{x^6}=\frac{1}{\cos 6 \theta+i \sin 6 \theta}\) = cos 6θ – i sin 6θ
∴ \(\left(x^6+\frac{1}{x^6}\right)\) = cos 6θ + i sin 6θ + cos 6θ – i sin 6θ = 2 cos 6θ

Question 4.
Form a quadratic equation whose roots are 7 ± 2√5.
Solution:
Let α = 7 + 2√5 and β = 7 – 2√5
α + β = 7 + 2√5 + 7 – 2√5 = 14
αβ = (7 + 2√5) (7 – 2√5)
= 49 – 20
= 29
Required quadratic equation is x² – (α + β)x + αβ = 0
∴ x² – 14x + 29 = 0

Question 5.
If -1, 2, and α are the roots of 2x³ + x² – 7x – 6 = 0, find α.
Solution:
Since -1, 2, α are the roots of the equation 2x³ + x² – 7x – 6 = 0
∴ s₁ = \(\frac{-1}{2}\)
⇒ -1 + 2 + α = \(\frac{-1}{2}\)
⇒ α + 1 = \(\frac{-1}{2}\)
⇒ α = \(\frac{-1}{2}\) – 1
⇒ α = \(\frac{-3}{2}\)

Question 6.
Find the number of ways of arranging the letters of the word MATHEMATICS.
Solution:
The word MATHEMATICS contains 11 letters in which 2M’s, 2A’s, and 2T’s rest are different.
∴ The number of ways of arranging the letters of the MATHEMATICS is \(\frac{11 !}{2 ! 2 ! 2 !}=\frac{11 !}{(2 !)^3}\)

Question 7.
If ⁿC₅ = ⁿC₆, then find ¹³C_n.
Solution:
Given ⁿC₅ = ⁿC₆
⇒ n = 5 + 6 = 11
∴ ¹³C_n = ¹³C₁₁
= ¹³C₂ [∵ ⁿC_r = ⁿC_n-r]
= \(\frac{13.12}{2}\)
= 78

Question 8.
Prove that C₀ + 2.C₁ + 4.C₂ + 8.C₃ + ………. + 2ⁿ . C_n = 3ⁿ.
Solution:

Question 9.
Find the mean deviation about the median for the following data:
4, 6, 9, 3, 10, 13, 2
Solution:
Given data points are 4, 6, 9, 3, 10, 13, 2
Now arranging data points in ascending order
2, 3, 4, 6, 9, 10, 13
∴ Median = 6
Absolute values |6 – 2|, |6 – 3|, |6 – 4|, |6 – 6|, |6 – 9|, |6 – 10|, |6 – 13| = 4, 3, 2, 0, 3, 4, 7
∴ Mean deviation about the median = \(\frac{4+3+2+0+3+4+7}{7}\)
= \(\frac{23}{7}\)
= 3.28

Question 10.
A Poisson variable satisfies P(X = 1) = P(X = 2). Find P(X = 5).
Solution:
X follows a Poisson distribution with parameter λ.

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Attempt any five questions.
• Each question carries four marks.

Question 11.
Show that the points in the Argand diagram represented by the complex numbers 2 + 2i, -2 – 2i, -2√3 + 2√3i are the vertices of an equilateral triangle.
Solution:
Let A, B, and C be the points in the Argand plane.
∴ A = (2, 2), B = (-2, -2), C = (-2√3, 2√3)

∴ AB = BC = CA
∴ A, B, and C are the vertices of an equilateral triangle.

Question 12.
Prove that \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie in between 1 and 4, if x is real.
Solution:

= \(\frac{4 x+1}{3 x^2+4 x+1}\)
⇒ 3yx² + 4yx + 4 = 4x + 1
⇒ 3yx² + (4y – 4)x + (y – 1) = 0
x ∈ R ⇒ (4y – 4)² – 4(3y)(y – 1) ≥ 0
⇒ 16y² – 32y + 16 – 12y² + 12y ≥ 0
⇒ 4y² – 20y + 16 ≥ 0
⇒ y² – 5y – 4 ≥ 0
⇒ (y – 1) (y – 4) ≥ 0
⇒ y ≥ 0 (or) y ≥ 4
∴ \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4.

Question 13.
Find the sum of all 4 digit numbers that can be formed using the digits 1, 3, 5, 7, 9.
Solution:
Given digits are 1, 3, 5, 7, 9
The no.of four-digit numbers that can be formed using the digits 1, 3, 5, 7, 9 is ⁵P₄ = 120.
We first find the sum of the digits in the unit place of all these 120 numbers.
If we fill the unit place with 1 then the remaining 3 places can be filled with the remaining 4 digits it can be done in ⁴P₃ ways.
Similarly, each digit 3, 5, 7, 9 appears 24 times in units place.
By adding all these digits, we get
⁴P₃ × 1 + ⁴P₃ × 3 + ⁴P₃ × 5 + ⁴P₃ × 7 + ⁴P₃ × 9
= ⁴P₃ × (1 + 3 + 5 + 7 + 9)
= ⁴P₃ × 25
Similarly, the sum of the digits in ten’s place value as ⁴P3 × 25 × 10
Similarly, the values of the sum of the digits 100’s place and 1000’s places are ⁴P₃ × 25 × 100 and ⁴P₃ × 25 × 1000
Hence the sum of all the 4-digit numbers formed by using the digits 1, 3, 5, 7, 9 is ⁴P₃ × 25 × 1 + ⁴P₃ × 25 × 10 + ⁴P₃ × 25 × 100 + ⁴P₃ × 25 × 1000
= ⁴P₃ × 25 × (1 + 10 + 100 + 1000)
= ⁴P₃ × 25 × 1111
= 24 × 25 × 1111
= 6,66,600

Question 14.
Find the number of ways of selecting a cricket team of 11 players from 7 batsmen and 6 bowlers, such that there will be atleast 5 bowlers in the team.
Solution:
Since the team consists of atleast 5 bowlers, the selection may be of the following types.

	Batsmen (7)	Bowlers (6)
Type 1	6	5
Type 2	5	6

The no. of selections is first type = ⁷C₆ × ⁶C₅ = 7 × 6 = 42
The no. of selections in second type = ⁷C₅ × ⁶C₆ = 21 × 1 = 21
∴ The required number of ways of selecting the cricket team = 42 + 21 = 63

Question 15.
Resolve the fraction \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}\) into partial fraction.
Solution:
Let \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+2}\)
⇒ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A\left(x^2+2\right)+(B x+C)(x-1)}{(x-1)\left(x^2+2\right)}\)
⇒ 2x² + 3x + 4 = A(x² + 2) + (Bx + C) (x – 1) ………(1)
Put x = 1
2 + 3 + 4 = A(1 + 2)
⇒ 9 = 3A
⇒ A = 3
Comparing the co-efficient of x² and constant terms in (1)
2 = A + B
⇒ 2 = 3 + B
⇒ B = -1
4 = 2A – C
⇒ 4 = 2(3) – C
⇒ C = 6 – 4
⇒ C = 2
∴ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{-x+2}{x^2+2}\)
∴ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{2-x}{x^2+2}\)

Question 16.
Suppose A and B are independent events with P(A) = 0.6 and P(B) = 0.7. Then compute:
(i) P(A ∩ B)
(ii) P(A ∪ B)
(iii) P(B/A)
(iv) P(A^C ∩ B^C)
Solution:
Given A, B are independent events and P(A) = 0.6, P(B) = 0.7
(i) P(A ∩ B) = P(A) P(B)
= (0.6) (0.7)
= 0.42

(ii) P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.6 + 0.7 – 0.42
= 0.88

(iii) P(B/A) = P(B) = 0.7

(iv) P(A^C ∩ B^C) = P(A^C) . P(B^C) (∵ Since A^C, B^C are also independent events)
= [1 – P(A)] [1 – P(B)]
= [1 – 0.6] [1 – 0.7]
= (0.4)(0.3)
= 0.12

Question 17.
A, B, C are three horses in a race. The probability of A winning the race is twice that of B and the probability of B is twice that of C. What are the probabilities of A, B, and C to win the race?
Solution:
If A, B, C are three independent events of an experiment such that P(A ∩ B^C ∩ C^C) = \(\frac{1}{4}\), P(A^C ∩ B ∩ C^C) = \(\frac{1}{8}\), P(A^C ∩ B^C ∩ C^C) = \(\frac{1}{4}\) then find P(A), P(B) and P(C).
Since A, B, C are independent events.

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Attempt any five questions.
• Each question carries seven marks.

Question 18.
If cos α + cos β + cos γ = 0 = sin α + sin β + sin γ, then prove that cos²α + cos²β + cos²γ = \(\frac{3}{2}\) = sin²α + sin²β + sin²γ.
Solution:
Let a = cos α + i sin α
b = cos β + i sin β
c = cos γ + i sin γ
a + b + c = (cos α + i sin α) + (cos β + i sin β) + (cos γ + i sin γ)
= (cos α + cos β + cos γ) + i (cos α + cos β + cos γ)
= 0 + i(0)
= 0
∴ a + b + c = 0
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{\cos \alpha+i \sin \alpha}+\frac{1}{\cos \beta+i \sin \beta}+\frac{1}{\cos \gamma+i \sin \gamma}\)
\(\frac{b c+c a+a b}{a b c}\) = cos α – i sin α + cos β – i sin β + cos γ – i sin γ
= (cos α + cos β + cos γ) + i(sin α + sin β + sin γ)
= 0 – i(0)
= 0
∴ ab + bc + ca = 0
(a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
⇒ 0 = a² + b² + c² + 2(0)
⇒ a² + b² + c² = 0
⇒ (cos α + i sin α)² + (cos β + i sin β)² + (cos γ + i sin γ)² = 0
⇒ cos 2α + i sin 2α + cos 2β + i sin 2β + cos 2γ + i sin 2γ = 0
⇒ (cos 2α + cos 2β + cos 2γ) + i (sin 2α + cos 2β + sin 2γ) = 0
Equation real parts on both sides, we have
cos 2α + cos 2β + cos 2γ = 0
⇒ 1 – 2 sin²α + 1 – 2 sin²β + 1 – 2 sin²γ = 0
⇒ 3 = 2(sin²α + sin²β + sin²γ)
⇒ sin²α + sin²β + sin²γ = \(\frac{3}{2}\)
Again cos 2α + cos 2β + cos 2γ = 0
⇒ 2 cos²α – 1 + 2 cos²β – 1 + 2 cos²γ – 1 = 0
⇒ 2(cos²α + cos²β + 2 cos²γ) = 3
⇒ cos²α + cos²β + cos²γ = \(\frac{3}{2}\)
∴ cos²α + cos²β + cos²γ = \(\frac{3}{2}\) = sin²α + sin²β + sin²γ

Question 19.
Solve the equation x⁴ – 10x³ + 26x² – 10x + 1 = 0.
Solution:
Given x⁴ – 10x³ + 26x² – 10x + 1 = 0
⇒ x² – 10x + 26 – \(\text { 10. } \frac{1}{x}+\frac{1}{x^2}\) = 0
⇒ \(\left(x^2+\frac{1}{x^2}\right)-10\left(x+\frac{1}{x}\right)\) + 26 = 0
Let x + \(\frac{1}{x}\) = t
Then x² + \(\frac{1}{x^2}\) = t² – 2
∴ (t² – 2) – 10t + 26 = 0
⇒ t² – 2 – 10t + 26 = 0
⇒ t² – 10t + 24 = 0
⇒ t² – 4t – 6t + 24 = 0
⇒ t(t – 4) – 6(t – 4) = 0
⇒ (t – 4) (t – 6) = 0
⇒ t = 4 (or) t = 6
∴ x + \(\frac{1}{x}\) = 4
⇒ x² + 1 = 4x
⇒ x² – 4x + 1 = 0
⇒ x = \(\frac{-(-4) \pm \sqrt{16-4.1 .1}}{2.1}\)
⇒ x = \(\frac{4 \pm \sqrt{12}}{2}\)
⇒ x = \(\frac{4 \pm 2 \sqrt{3}}{2}\)
⇒ x = 2 ± √3
∴ x + \(\frac{1}{x}\) = 6
⇒ x² + 1 = 6x
⇒ x² – 6x + 1 = 0
⇒ x = \(\frac{-(-6) \pm \sqrt{36-4.1 .1}}{2.1}\)
⇒ x = \(\frac{6 \pm \sqrt{32}}{2}\)
⇒ x = \(\frac{6 \pm 4 \sqrt{2}}{2}\)
⇒ x = 3 ± 2√2
∴ The roots are 2 ± √3, 3 ± 2√2

Question 20.
If the coefficients of r^th, (r + 1)^th and (r + 2)^nd terms in the expansion of (1 + x)ⁿ are in A.P. Then show that n² – (4r + 1)n + 4r² – 2 = 0.
Solution:
The coefficients of r^th, (r + 1)^th, and (r + 2)^th terms in the expansion of (1 + x)³ are ⁿC_r-1, ⁿC_r, and ⁿC_r+1 respectively.
Given ⁿC_r-1 + ⁿC_r+1 = 2 ⁿC_r are in A.P.
∴ ⁿC_r-1 + ⁿC_r+1 = 2 ⁿC_r

⇒ (n – r) (n – r + 1) = (r + 1) (2n – 3r + 2)
⇒ n² – 2nr + r² + n – r = 2nr – 3r² + 2r + 2n – 3r + 2
⇒ n² – 4nr + 4r² – n – 2 = 0
⇒ n² – (4r + 1)n + 4r² – 2 = 0

Question 21.
If x = \(\frac{1.3}{3.6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6.9}+\frac{1 \cdot 3 \cdot 5 \cdot 7}{3 \cdot 6 \cdot 9 \cdot 12}+\ldots\), then prove that 9x² + 24x = 11.
Solution:


⇒ 4 + 3x = 3√3
⇒ (4 + 3x)² = 27
⇒ 16 + 9x² + 24x = 27
∴ 9x² + 24x = 11

Question 22.
Find the mean deviation about the mean for the following data:

Marks Obtained	0-10	10-20	20-30	30-40	40-50
No. of Students	5	8	15	16	6

Solution:
Taking the assumed mean a = 25 and h = 10
Construct the table

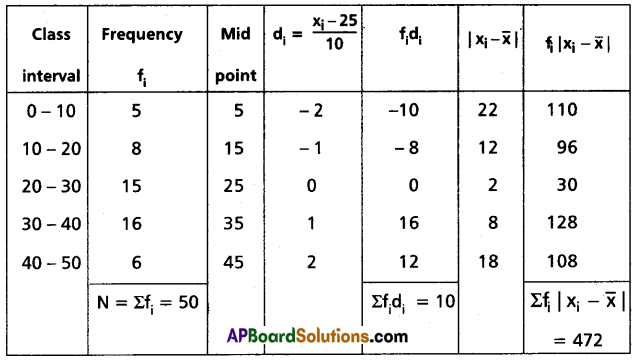
\(\bar{x}=\left(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\mathrm{N}}\right) \mathrm{h}\)
= 25 + (\(\frac{10}{50}\))10
= 27
∴ Mean deviation from the mean = \(\frac{1}{N} \Sigma f_i\left|x_i-\bar{x}\right|\)
= \(\frac{10}{50}\)(472)
= 9.44

Question 23.
State and prove the addition theorem on probability.
Solution:
Statement: If E₁ and E₂ are any two events of a random experiment and P is the probability function.
Then P(E₁ ∪ E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)
Case (i): When E₁ ∩ E₂ = φ
E₁ ∩ E₂ = φ
⇒ P (E₁ ∩ E₂) = 0
∴ P(E₁ ∪ E₂) = P(E₁) + P(E₂) [∵ from the union axiom]
= P(E₁) + P(E₂) – 0
= P(E₁) + P(E₂) – P(E₁ ∩ E₂)
Case (ii): When E₁ ∩ E₂ = φ
∴ E₁ ∪ E₂ can be expressed as union of 2 mutually exclusive events E₁ – E₂, E₂.
Hence, E₁ ∪ E₂ = (E₁ – E₂) ∪ E₂
Also (E₁ – E₂) ∩ E₂ = φ
∴ P(E₁ ∪ E₂) = P[(E₁ – E₂) ∪ E₂]
P(E₁ ∪ E₂) = P(E₁ – E₂) + P(E₂) ………(1) [∵ from the union axiom]
Also, E₁ can be expressed as the union of 2 mutually exclusive events E₁ – E₂, E₁ ∩ E₂.
Hence, E₁ = (E₁ – E₂) ∪ (E₁ ∩ E₂)
Also (E₁ – E₂) ∩ (E₁ ∩ E₂) = φ
∴ P(E₁) = P(E₁ – E₂) ∪ (E₁ ∩ E₂)] = P(E₁ – E₂) + P(E₁ ∩ E₂)
⇒ P(E₁ – E₂) = P(E₁) – P(E₁ ∩ E₂)
From (1 ),
P(E₁ ∪ E₂) = P(E₁) – P(E₁ ∩ E₂) + P(E₂) = P(E₁) + P(E₂) – P(E₁ ∩ E₂)

Question 24.
A random variable ‘X’ has the following probability distribution.

X = x	0	1	2	3	4	5	6	7
P(X = x)	0	K	2K	2K	3K	K2	2K2	7K2 + K

Find:
(i) K
(ii) Mean
(iii) P(0 < x < 5)
Solution:
We know P(X = x) = 1
⇒ P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) = 1
⇒ 0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
⇒ 10k² + 9k = 1
⇒ 10k² + 9k – 1 = 0
⇒ 10k² + 10k – k – 1 = 0
⇒ 10k(k + 1) – 1(k + 1) = 0
⇒ (k + 1) (10k – 1) = 0
⇒ k = -1 (or) \(\frac{1}{10}\)

(i) k = \(\frac{1}{10}\) Since k > 0

(ii) Mean = 0 (P = 0) + 1 P(X = 1) + 2 P(X = 2) + 3 P(X = 3) + 4 P(X = 4) + 5 P(X = 5) + 6 P(X = 6) + 7 P(X = 7)
= 0(0) + 1(k) + 2(2k) + 3(2k) + 4(3k) + 5(k²) + 6(2k²) + 7(7k² + k)
= 0 + k + 4k + 6k + 12k + 5k² + 12k² + 49k² + 7k
= 66k² + 30k
= \(66\left(\frac{1}{10}\right)^2+30\left(\frac{1}{10}\right)\)
= 66(\(\frac{1}{100}\)) + 3
= 0.66 + 3
= 3.66

(iii) P(0 < x < 5) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= k + 2k + 2k + 3k
= 8k
= 8(\(\frac{1}{10}\))
=0.8
∴ P(0 < x < 5) = 0.8