TS Inter 1st Year Maths 1B Question Paper March 2018

Access to a variety of TS Inter 1st Year Maths 1B Model Papers and TS Inter 1st Year Maths 1B Question Paper March 2018 allows students to familiarize themselves with different question patterns.

TS Inter 1st Year Maths 1B Question Paper March 2018

Time : 3 Hours
Max. Marks : 75

Note : This question paper consists of THREE sections A, B and C.

Section – A
(10 × 2 = 20 Marks)

I. Very short answer type questions :

1. Answer all the questions.
2. Each question carries two marks.

Question 1.
Find the value of x, if the slope of the line passing through (2, 5) and (x, 3) is 2.
Solution:
Given the Slope of the line passing through (2, 5) and (x, 3) is 2
⇒ \(\frac{3-5}{x-2}\) = 2
⇒ -2 = 2x – 4
⇒ 2x = 2
⇒ x = 1

Question 2.
Transform the equation x + y + 1 =0 into normal form.
Solution:
Given x + y + 1 = 0
⇒ x + y = -1
⇒ -x – y = 1
⇒ \(\frac{-x-y}{\sqrt{2}}\) = \(\frac{1}{\sqrt{2}}\)
⇒ \(x\left(\frac{-1}{\sqrt{2}}\right)+y\left(\frac{-1}{\sqrt{2}}\right)\) = \(\frac{1}{\sqrt{2}}\)
⇒ x cos \(\frac{5 \pi}{4}\) + y sin \(\frac{5 \pi}{4}\) = \(\frac{1}{\sqrt{2}}\) which is the required normal form.

Question 3.
Find the ratio in which the xz-plane divides the line joining A(-2, 3, 4) and B(1, 2, 3).
Solution:
Given A = (-2, 3, 4)
B = (1, 2, 3)
The XZ – Plane divides the line joining AB in the ratio
= -y₁ : y₂ = -3 : 2 = 3 : 2 externally.

Question 4.
Find the intercepts of the plane 4x + 3y – 2z + 2 = 0 on the Co-ordinate axes.
Solution:
Given plane equation is 4x + 3y – 2z + 2 = 0
⇒ 4x + 3y – 2z = – 2
⇒ \(\frac{4 x}{-2}+\frac{3 y}{-2}-\frac{2 z}{-2}\) = 1
⇒ \(\frac{x}{\frac{-1}{2}}+\frac{y}{\frac{-2}{3}}+\frac{z}{1}\) = 1
∴ X – intercept = \(\frac{-1}{2}\)
Y – intercept = \(\frac{-2}{3}\)
Z- intercept = 1.

Question 5.
Compute \(\lim _{x \rightarrow 0}\left(\frac{\sin a x}{\sin b x}\right)\)|, b ≠ 0, a ≠ b.
Solution:

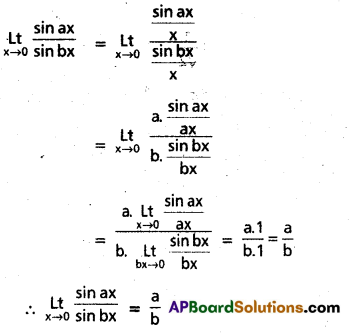
Question 6.
Compute \(\lim _{x \rightarrow \pi / 2}\left(\frac{\cos x}{x-\pi / 2}\right)\)
Solution:

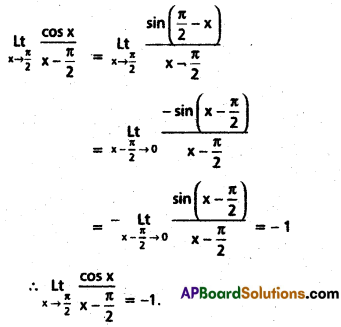
Question 7.
If y = \(\frac{a-x}{a+x}\)(x ≠ -a), find \(\frac{d y}{d x}\).
Solution:
Given y = \(\frac{a-x}{a+x}\)
differentiating w.r.to ‘x’ on both sides, we have

Question 8.
If y = (cot^-1 x³)², find \(\frac{d y}{d x}\).
Solution:
Given y = (cot^-1 x³)²
differentiate w.r.to ‘x’ on both sides, we have

Question 9.
If the increase in the side of a square is 2%, then find the approximate percentage of increase in its areas.
Solution:
Let x, A be the side and area of a square respectively.
Given \(\frac{\Delta x}{x}\) × 100 = 2
A = x²
∆A = 2x ∆x
\(\frac{\Delta \mathrm{A}}{\mathrm{A}}\) × 100 = \(\frac{2 x \Delta x}{x^2}\) × 100
= 2\(\frac{\Delta x}{x}\) × 100
∴ The approximate increase in the area is 4%.

Question 10.
Find the value of C in Lagrange’s mean value theorem for the function f(x) = x² – 1 on [2, 3].
Solution:
Let f(x) = x² – 1
Since f is a second degree polynomial
∴ f is continuous on [2, 3] and
f is derivable on (2, 3)
∴ f satisfies all the conditions of
Lagrange’s mean value theorem
∴ There c ∈ (2, 3) such that
f'(c) = \(\frac{f(3)-f(2)}{3-2}\)
⇒ f(c) = f(3) – f(2) ……. (1)
f(x) = x² – 1 ⇒ f'(x) = 2x
⇒ f'(c) = 2c
f(3) = 3² – 1 = 9 – 1 = 8
f(2) = 2² – 1 = 4 – 1 = 3
From (1)
2c = 8 – 3
⇒ 2c = 5
⇒ c = 5/2 ∈ (2, 3)

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions :

1. Attempt any Five questions.
2. Each question carries four marks.

Question 11.
Find the locus of the third vertex of a right angled triangle, the ends of whose hypotenuse are (4, 0) and (0, 4).
Solution:
Let A = (4, 0)
B = (0, 4)
Let p(x₁, y₁) be any point on the focus.

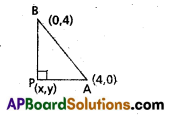
From fig
⇒ PA² + PB² + AB²
⇒ (x₁ – 4)² + (y₁ – 0)² + (x₁ – 0)² + (y₁ – 4)²
= (4 – 0)² + (0 – 4)²
⇒ \(x_1^2\) – 8x₁ + 16 + \(y_1^2\) + \(x_1^2\) + \(y_1^2\) – 8y₁ + 16 = 16 + 16
⇒ \(2 x_1^2\) + \(2 y_1^2\) – 8x₁ – 8y₁ = 0
⇒ \(x_1^2\) + \(y_1^2\) – 4x₁ – 4y₁ = 0
The focus of P is x² + y² – 4x – 4y = 0.

Question 12.
When the axes are rotated through an angle \(\frac{\pi}{6}\), find the transformed equation of x² + 2\(\sqrt{3}\)xy – y² = 2a².
Solution:

Question 13.
Find the value of k, if the liens 2x – 3y + k = 0, 3x – 4y – 13 = 0 and 8x – 11y – 33 = 0 are concurrent.
Solution:
Given line equations are
2x – 3y + k = 0 ……. (1)
3x – 4y – 13 = 0 …….. (2)
8x – 11y – 33 = 0 …… (3)
solving (2) and (1)

The point of intersection of (2) and (3) is (11, 5)
Since (1), (2), (3) are concurrent
∴ The point (11, 5) lies on (1)
∴ 2(11) – 3(5) + k = 0
⇒ 22 – 15 + k = 0
⇒ k + 7 = 0

Question 14.
Find the real constants a,b so that the function f given by

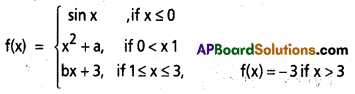
is continuous on R.
Solution:
Given f(x) sinx, if x ≤ 0

Since f is continuous at x = 3

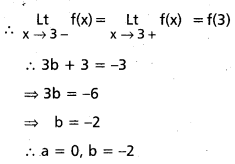
Question 15.
Find the derivative of x sin x from the first principle.
Solution:
Let f(x) = x sin x
By first principle

Question 16.
Show that at any point (x, y) on the curve y = b e^x/a, the length of the sub-tangent is a constant and the length of the subnormal is \(\frac{y^2}{a} .\)
Solution:
Given curve equation is y = be^x/a
differentiating w.r.to ‘x’ on both sides, we have

Question 17.
A particle is moving along a line according to S = f(t) = 4t³ – 3t² + 5t – 1 where S is measured in metres and t is measured in seconds. Find the velocity and acceleration at time t. At what time the acceleration is zero ?
Solution:
Given S = f(t) = 4t³ – 3t² + 5t – 1
Velocity \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 4(3t²) – 3 (2t) + 5(1) – 0
= 12t² – 6t + 5
Acceleration \(\frac{\mathrm{d}^2 \mathrm{~s}}{\mathrm{dt}^2}\) = 12 (2t) – 6(1) + 0
⇒ 24t = 6
⇒ t = \(\frac{1}{4}\)
⇒ 24t = 6
⇒ t = 4
∴ Acceleration is zero when t = \(\frac{1}{4}\) sec.

Section – C

III. Long answer type questions :

1. Attempt Any Five questions.
2. Each question carries Seven marks.

Question 18.
Find the circumcenter of the triangle whose vertices are (1, 3), (-3, 5) and (5,-1).
Solution:
Let A = (1, 3), B = (-3, 5), C = (5, -1)
Let s(α, β) be the circumcenter of the ∆ABC
∴ SA = SB = SC
SA = SB .

Question 19.
If the equation ax² + 2hxy + by² = 0 represents a pair of straight lines, then show that the angle between the lines is given by
cosθ = \(\frac{|a+b|}{\sqrt{(a-b)^2+4 h^2}}\)
Solution:
The equation ax² + 2hxy + by² = 0 ……. (1)
represent a pain of straight lines passing through the origin.
Let (1) represent lines be l₁x + m₁x = 0 …… (2) and
l₂x + m₂y = 0 …… (3)

Question 20.
Show that the lines joining the origin to the points of intersection of the curve x² – xy + y² + 3x + 3y – 2 = 0 and the straight line x – y – \(\sqrt{2}\) = 0 are mutually perpendicular.
Solution:
Equation of the curve is
x² – xy + y² + 3x + 3y – 2 = 0 …. (1)

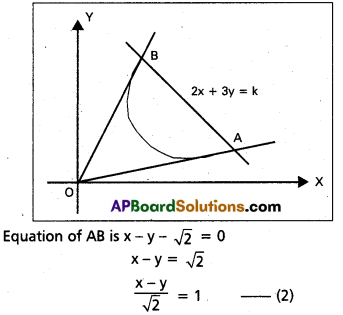
Homogenising, (1) with the help of (2) combined equation of OA, OB is

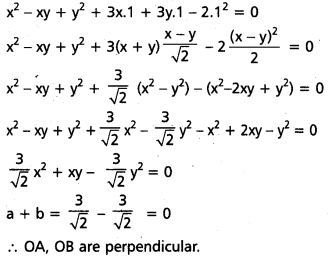
Question 21.
Find the angle between two diagonals of a cube.

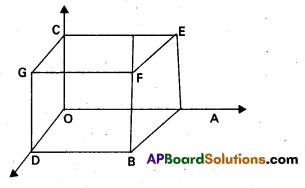
Solution:
Let ‘O’ one of the vertices of the cube taken as origin and the three sides OA, OB, OC are taken as Co-ordinate axes. Let OA = OB = OC = a the four diagonals are \(\overrightarrow{\mathrm{OF}}\), \(\overrightarrow{\mathrm{AG}}\), \(\overrightarrow{\mathrm{DE}}\) and \(\overrightarrow{\mathrm{BC}}\)
The Co-ordinates of the vertices of the cube are 0(0, 0, 0), A(a, 0, 0), B(0, a, 0), C(0, 0, a)
F(a, a, 0), D(a, a, 0), E(a, 0, a), G(0, a, a)
D.Rs of OF are (a – 0, a – 0, a – 0) = (a, a, a)
D.Rs of AG are (0 – a, a – 0, a – 0) = (-a, a, a)
If O is the angle between the diagonals OF and AG

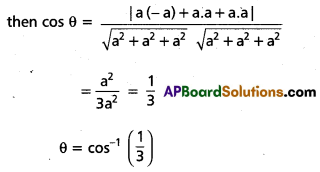
Similarly the angle between any pair of diagonals can be shown to be cos^-1\(\left(\frac{1}{3}\right)\).

Question 22.
If y = Tan^-1\(\left(\frac{\sqrt{1+x^2}+\sqrt{1-x^2}}{\sqrt{1+x^2}-\sqrt{1-x^2}}\right)\) for 0 < |x| < 1, find \(\frac{d y}{d x}\)
Solution:

Question 23.
Show that the equation of the tangent to the curve
\(\left(\frac{x}{a}\right)^n+\left(\frac{y}{b}\right)^n\) = 2 (a ≠ 0, b ≠ 0) at the point (a, b) is \(\frac{x}{a}+\frac{y}{b}\) = 2
Solution:


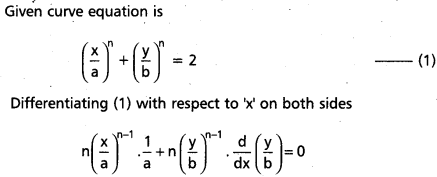
∴ The equation of the tangent to the curve at the point (a, b) is y – y₁ = m(x – x₁)

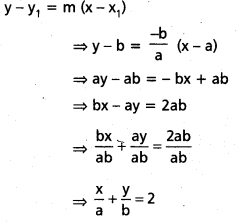
Question 24.
From a rectangular sheet of dimensions 30cm × 80 cm four equal squares of side x cm are removed at the corners and the sides are then turned up so as to form an open rectangular box. Find the value of x, so that the volume of the box is the greatest ?
Solution:
Length of the box = 80 – 2x = l
Breadth of the box = 30 – 2x = b

f(x) is maximum when x = \(\frac{20}{3}\)
Volume of the box is maximum when x = \(\frac{20}{3}\) cm