TS Inter 1st Year Maths 1A Question Paper May 2019

Thoroughly analyzing TS Inter 1st Year Maths 1A Model Papers and TS Inter 1st Year Maths 1A Question Paper May 2019 helps students identify their strengths and weaknesses.

TS Inter 1st Year Maths 1A Question Paper May 2019

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of three sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer All the questions.
• Each question carries Two marks.

Question 1.
If f: R – {0} → R is defined by f(x) = x³ – \(\frac{1}{x^3}\), then show that f(x) + f(\(\frac{1}{x}\)) = 0.
Solution:

Question 2.
Find the domain of the real valued function f(x) = \(\frac{2 x^2-5 x+7}{(x-1)(x-2)(x-3)}\).
Solution:
Given f(x) = \(\frac{2 x^2-5 x+7}{(x-1)(x-2)(x-3)}\)
f(x) ∈ R ⇒ (x – 1) (x – 2) (x – 3) ≠ 0
⇒ x ≠ 1, 2, 3
∴ Domain of f = R – {1, 2, 3}

Question 3.
If A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right]\) and det A = 45, then find x.
Solution:
Given A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right]\)
det A = 45
⇒ \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right]\) = 45
⇒ 1(3x + 24) = 45
⇒ 3x = 45 – 24
⇒ 3x = 21
⇒ x = 7

Question 4.
Find the trace of \(\left[\begin{array}{ccc}
1 & 3 & -5 \\
2 & -1 & 5 \\
2 & 0 & 1
\end{array}\right]\).
Solution:
Let A = \(\left[\begin{array}{ccc}
1 & 3 & -5 \\
2 & -1 & 5 \\
2 & 0 & 1
\end{array}\right]\)
Trace of (A) = 1 + (-1) + 1
= 1 – 1 + 1
= 1

Question 5.
Let \(\overline{\mathrm{a}}=\overline{\mathrm{i}}+2 \overline{\mathrm{j}}+3 \overline{\mathrm{k}}\) and \(\overline{\mathrm{b}}=3 \overline{\mathrm{i}}+\overline{\mathrm{j}}\). Find the unit vector in the direction of \(\overline{\mathrm{a}}+\overline{\mathrm{b}}\).
Solution:
Given \(\overline{\mathrm{a}}=\overline{\mathrm{i}}+2 \overline{\mathrm{j}}+3 \overline{\mathrm{k}}\)
\(\overline{\mathrm{b}}=3 \overline{\mathrm{i}}+\overline{\mathrm{j}}\)

Question 6.
Find the vector equation of the line passing through the point \(2 \bar{i}+3 \bar{j}+\bar{k}\) and parallel to the vector \(4 \bar{i}-2 \bar{j}+3 \bar{k}\).
Solution:

Question 7.
Find the angle between the vectors \(\overline{\mathrm{i}}+2 \overline{\mathrm{j}}+3 \overline{\mathrm{k}}\) and \(3 \overline{\mathbf{i}}-2 \overline{\mathbf{j}}+2 \overline{\mathrm{k}}\).
Solution:

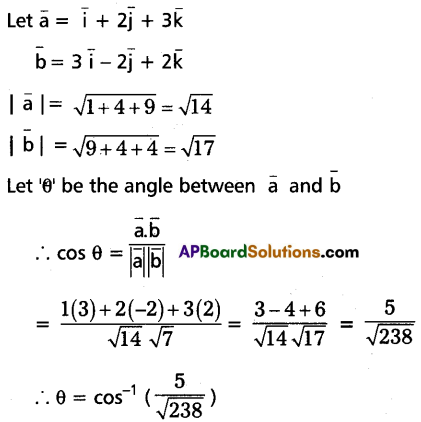
Question 8.
Express \(\frac{\left(\sqrt{3} \cos 25^{\circ}+\sin 25^{\circ}\right)}{2}\) as a sin of an angle.
Solution:
\(\frac{\left(\sqrt{3} \cos 25^{\circ}+\sin 25^{\circ}\right)}{2}=\frac{\sqrt{3} \cos 25^{\circ}}{2}+\frac{\sin 25^{\circ}}{2}\)
= \(\frac{\sqrt{3}}{2}\) cos 25° + \(\frac{1}{2}\) sin 25°
= sin 60° cos 25° + cos 60° sin 25°
= sin (60° + 25°)
= sin 85°

Question 9.
Express \(\frac{1-\cos \theta+\sin \theta}{1+\cos \theta+\sin \theta}\) in terms of \(\tan \frac{\theta}{2}\).
Solution:

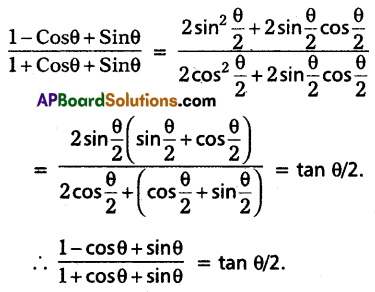
Question 10.
Prove that \(\frac{\tanh x}{{sech} x-1}+\frac{\tanh x}{{sech} x+1}\) = -2 cosech x, for x ≠ 0.
Solution:

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Attempt any Five questions.
• Each question carries Four marks.

Question 11.
If A = \(\left[\begin{array}{ccc}
2 & -1 & 2 \\
1 & 3 & -4
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & -2 \\
-3 & 0 \\
5 & 4
\end{array}\right]\), then show that (AB)’ = B’A’.
Solution:

Question 12.
Verify whether the triangle formed by the vectors \(3 \overline{\mathrm{i}}+5 \overline{\mathrm{j}}+2 \overline{\mathrm{k}}\), \(2 \overline{\mathrm{i}}-3 \overline{\mathrm{j}}-5 \bar{k},-5 \overline{\mathrm{i}}-2 \overline{\mathrm{j}}+3 \bar{k}\) is equilateral or not.
Solution:

∴ AB = BC = CA
∴ The given vectors form an equilateral triangle.

Question 13.
If θ is the angle between vectors \(\overline{\mathbf{i}}+\overline{\mathbf{j}}\) and \(\overline{\mathbf{j}}+\overline{\mathbf{k}}\), then find sin θ.
Solution:
Let \(\overline{\mathrm{a}}=\overline{\mathrm{i}}+\overline{\mathrm{j}}\)
\(\bar{b}=\bar{j}+\bar{k}\)

Question 14.
Prove that \(\frac{\cos ^3 \theta-\cos 3 \theta}{\cos \theta}+\frac{\sin ^3 \theta+\sin 3 \theta}{\sin \theta}\) = 3.
Solution:

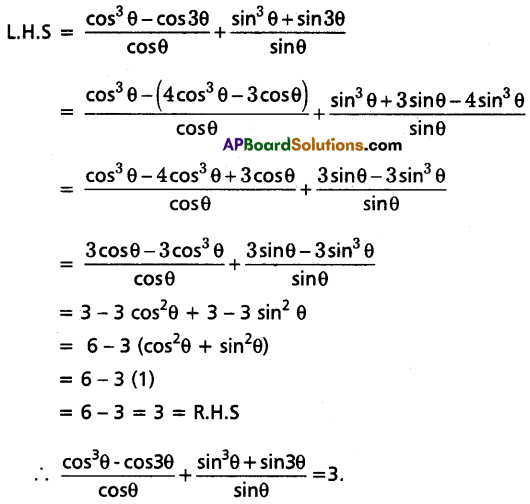
Question 15.
If α, β are the solutions of the equation a cos θ + b sin θ = c, where a, b, c ∈ R and if a² + b² > 0 and sin α ≠ sin β, then show that sin α + sin β = \(\frac{2 b c}{a^2+b^2}\).
Solution:
Given a cos θ + b sin θ = c
⇒ a cos θ = c – b sin θ
⇒ a² cos²θ = (c – b sin θ)²
⇒ a² (1 – sin²θ) = c² + b² sin²θ – 2bc sin θ
⇒ a² – a² sin²θ = c² + b² sin²θ – 2bc sin θ
⇒ (a² + b²) sin²θ – 2bc sin θ – (c² – a²) = 0 ………(1)
Since α and β are the solutions of the given equation.
∴ sin α, sin β are the roots of (1)
Sum of the roots sin α + sin β = \(\frac{-(-2 b c)}{a^2+b^2}=\frac{2 b c}{a^2+b^2}\).

Question 16.
Prove that \(\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}=\frac{S^2}{\Delta}\).
Solution:

Question 17.
Prove that \(\tan ^{-1}\left(\frac{1}{7}\right)+\tan ^{-1}\left(\frac{1}{13}\right)-\tan ^{-1}\left(\frac{2}{9}\right)\) = 0.
Solution:

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Attempt any FIVE questions.
• Each question carries Seven marks.

Question 18.
If f: A → B, g: B → C are any two bijective functions, then prove that gof: A → C is also a bijective function.
Solution:
Given f: A → B, g: B → C are two bijective functions.
f: A → B, g: B → C
⇒ gof: A → C.
(i) To prove gof: A → C is one-one
Let a₁, a₂ ∈ A.
(gof) (a₁) = (gof) (a₂)
⇒ g[f(a₁)] = g[f(a₂)]
⇒ f(a₁) = f(a₂) [∴ g is one-one]
⇒ a₁ = a₂ [∴ f is one-one]
∴ gof: A → C is one-one.
(ii) To prove gof: A → C is onto.
Let c ∈ C.
Since g: B → C is a bijection.
∴ There exists b ∈ B such that g(b) = c
Since f: A → B is a bijection.
∴ There exists a ∈ A such that f(a) = b
C = g(b)
= g(f(a))
= (gof) (a)
∴ There exists a ∈ A such that (gof) (a) = c.
∴ gof: A → C is onto.
∴ gof: A → C is one-one and onto.
∴ gof: A → C is bijection.

Question 19.
Using mathematical induction, prove the statement 1³ + 2³ + 3³ + …….. + n³ = \(\frac{\mathrm{n}^2(\mathrm{n}+1)^2}{4}\), ∀ n ∈ N.
Solution:
Let p(n) be the statement that
1³ + 2³ + 3³ + ……… + n³ = \(\frac{n^2(n+1)^2}{4}\)
If n = 1 then
L.H.S = 1³ = 1
R.H.S = \(\frac{1^2(1+1)^2}{4}=\frac{1(4)}{4}\) = 1
∴ L.H.S = R.H.S
∴ P(1) is true.
Assume that P(K) is true.
∴ 1³ + 2³ + 3³ + ……… + k³ = \(\frac{k^2(k+1)^2}{4}\)
1³ + 2³ + 3³ + …….. + k³ + (k + 1)³ = \(\frac{k^2(k+1)^2}{4}\) + (k + 1)³

∴ P(k + 1) is true.
By the principle of finite mathematical induction p(n) is true ∀ n ∈ N.
Hence 1³ + 2³ + 3³ + ……… + n³ = \(\frac{n^2(n+1)^2}{4}\) ∀ n ∈ N.

Question 20.
x + y + z = 1, 2x + 2y + 3z = 6, x + 4y + 9z = 3. Solve the system of equations by using the matrix inversion method.
Solution:
Given system of equations are
x + y + z = 1
2x + 2y + 3z = 6
x + 4y + 9z = 3
Given a system of equations can written as a matrix equation AX = B.

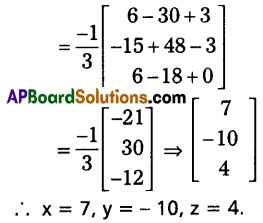
Question 21.
Show that \(\left|\begin{array}{lll}
1 & a^2 & a^3 \\
1 & b^2 & b^3 \\
1 & c^2 & c^3
\end{array}\right|\) = (a – b) (b – c) (c – a) (ab + bc + ca).

Question 22.
Find the shortest distance between the lines \(r=6 \bar{i}+2 \bar{j}+2 \bar{k}+t(\bar{i}-2 \bar{j}+2 \bar{k})\) and \(r=-4 \bar{i}-\bar{k}+s(3 \bar{i}-2 \bar{j}-2 \bar{k})\).
Solution:

Question 23.
If A + B + C = \(\frac{\pi}{2}\), then prove that cos 2A + cos 2B + cos 2C = 1 + 4 sin A sin B sin C.
Solution:
Given A + B + C = \(\frac{\pi}{2}\)
L.H.S = cos 2A + cos 2B + cos 2C
= \(2 \cos \left(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\right) \cos \left(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\right)\) + 1 – 2 sin²C
= 2 cos (A + B) cos (A – B) + 1 – 2 sin²C
= 1 + 2 cos (90° – C) cos (A – B) – 2 sin²C
= 1 + 2 sin C cos (A – B) – 2 sin²C
= 1 + 2 sin C [cos (A – B) – sin C]
= 1 + 2 sin C [cos (A – B) – sin {90° – (A + B)}]
= 1 + 2 sin C [cos(A – B) – cos (A + B)]
= 1 + 2 sin C [2 sin A sin B]
= 1 + 4 sin A sin B sin C
= R.H.S
∴ L.H.S = R.H.S
∴ cos 2A + cos 2B + cos 2C = 1 + 4 sin A sin B sin C.

Question 24.
In a ΔABC, prove that 4(r₁r₂ + r₂r₃+ r₃r₁) = (a + b + c)².
Solution:
L.H.S = 4(r₁r₂ + r₂r₃ + r₃r₁)

= 4s (3s – 2s)
= 4s (s)
= 4s²
= (2s)²
= (a + b + c)²
= R.H.S
∴ L.H.S = R.H.S
∴ 4(r₁r₂ + r₂r₃ + r₃r₁) = (a + b + c)²