TS 10th Class Maths Model Paper Set 7 with Solutions

The strategic use of TS 10th Class Maths Model Papers Set 7 can significantly enhance a student’s problem-solving skills.

TS SSC Maths Model Paper Set 7 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. Answer all the questions under Part – A on a separate answer book.
2. Write the answers to the questions under Part – B on the question paper itself and attach it to the answer book of Part – A.

Part – A (60 Marks)
Section – I (6 × 2 = 12 Marks)

Note:

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 1.
Is 7 × 5 × 3 × 2 + 3a composite number ? Justify your answer.
Answer:
Given number is 7 × 5 × 3 × 2 + 3
= 3(7 × 5 × 2 + 1)
= 3 × (70 + 1)
= 3 × 71
Here 3 and 71 are the prime numbers so the product of two primes is a composite number.
∴ 7 × 5 × 3 × 2 + 3 is a composite number.

Question 2.
p(x) = x² – 2x – 3, find the values of p(1) and p(0).
Answer:
Given polynomial is p(x) = x² – 2x – 3
p(1) = 1² – 2(1) – 3 = 1 – 2 – 3 = 1 – 5 = – 4
p(0) = 0² – 2(0) – 3 = 0 – 0 – 3 = – 3

Question 3.
Find the roots of x² – x – 12 = 0 using factorization method.
Answer:
x² – x – 12 = 0
x² – x – 12 = x² – 4x + 3x – 12
= x(x – 4) + 3(x – 4)
= (x – 4)(x + 3)
The roots of x² – x – 12 = 0 are the values of x for which (x – 4)(x + 3) = 0
x – 4 = 0 or x + 3 = 0
x = 4 or x = -3
Therefore the roots of x² – x -12 = 0 are 4 and -3.

Question 4.
Are the given triangles similar ?

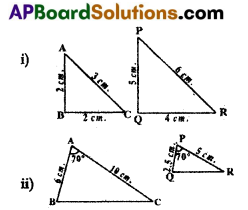
Answer:
i) No,
ii) No.

Question 5.
Consider the following situations. In each find out whether you need volume or area.
i) Quantity of water inside a bottle.
ii) Canvas need for making a tent.
Answer:
i) Volume
ii) Area.

Question 6.
A die is thrown once. Calculate the probability of getting a number less than 3.
Answer:
Possible outcomes in a single throw of a die is (1, 2, 3, 4, 5, 6} ∴ n(S) = 6
There are two numbers {1,2} less than 3.
∴ n(E) = 2
∴ Required probability = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\)

Section – II (6 × 4 = 24 Marks)

Note :

1. Answer ALL the following questions,
2. Each question carries 4 marks.

Question 7.
If log(\(\frac{x+y}{3}\)) = \(\frac{1}{2}\) (log x + log y) then prove that x² + y² = 7xy
Answer:
Given, log (\(\frac{x+y}{3}\)) = \(\frac{1}{2}\) (log x + log y)
log (\(\frac{x+y}{3}\)) = \(\frac{1}{2}\) log (xy) = log (xy)^1/2
⇒ \(\frac{x+y}{3}\) = (xy)^1/2
x + y = 3(xy)^1/2
squaring on both sides, (x + y)² = 9xy
x² + y² + 2xy = 9xy
x² + y² = 9xy – 2xy = 7xy
∴ x² + y² = 7xy

Question 8.
Obtain all other zeroes of x³ + 3x² – x – 3 if one of its zeroes is 1.
Answer:
Given polynomial x³ + 3x² – x – 3
One of its zeroes is 1
Therefore we can divide the polynomial by x – 1

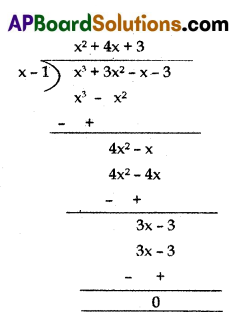
x³ + 3x² – x – 3
= (x – 1) (x² + 4x + 3)
= (x – 1) (x² + 3x + x + 3)
= (x – 1) (x (x + 3) + 1 (x + 3)
= (x – 1)(x + 3)(x + 1)
The other zeroes of the given polynomial are -3 and -1.

Question 9.
The outer dimensions of a bordered table are 72 cm and 108cm of the area of the table, excluding the border is 6400 cm². Write a quadratic equation.
Answer:
Let the width of the border be x cm
Length of the rectangle excluding the border = (108 – 2x) cm
Breadth of the rectangle excluding the border = (7x – 2x)cm
Area of the table excluding the border = (108 – 2x)(72 – 2x) = 6400.

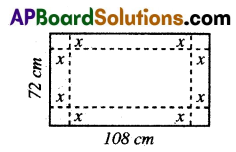
= 7776 – 216x – 144x + 4x² = 6400
4x² = 360x + 7776 – 6400 = 0
x² – 90x + 344 = 0

Question 10.
The king, queen and jack of clubs are removed from a pack of 52 playing cards and then the remaining pack is well shuffled. One card is selected from the remaining cards. Find the probability of getting:
i) a heart,
ii) a king,
iii) a club.
Answer:
Remaining cards = 52 – 3 = 49
P(heart) = \(\frac{13}{49}\); P(king) = \(\frac{3}{49}\)
P(club) = \(\frac{10}{49}\)

Question 11.
State whether the following statements are true or false. Justify your answer.
i) cot A is the product of cot and A.
ii) sin θ = \(\frac{4}{3}\) for some angle θ.
Answer:
i) False.
Cot A is used as an abbrevation for “the cotangent of the angle A.” It is the symbol which can not be separated.

ii) False.
The hypotenuse is the longest side in a right angled triangle. The value of Sin is always less than 1. (Refer here Sin θ = \(\frac{4}{3}\) which is greaterthan 1 and it is not possible for any θ.)

Question 12.
A person who is 1.65 m tall casts 1.8 in shadow. At the same instance, a lamp-post casts a shadow of 5.4 m. Find the height of the lamp-post
Answer:
In ΔABC and ΔPQR, ∠B = ∠Q = 90°, ∠C = ∠R (AC || PR, all the sun rays are parallel at any instance)
ΔABC ~ ΔPQR (by AA similarity)
\(\frac{A B}{P Q}\) = \(\frac{\mathrm{BC}}{\mathrm{QR}}\) (corresponding parts of similar triangles)
\(\frac{1.65}{P Q}=\frac{1.8}{5.4}\)
PQ = \(\frac{1.64 \times 5.4}{1.8}\) = 4.95 m
∴ The height of the lamp post is 4.95 m

Section – III (4 × 6 = 24 Marks)

Note :

1. Answer any 4 of the following questions,
2. Each question carries 6 marks.

Question 13.
If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first h terms.
Answer:
Sum of first 7 terms S_n = 49
S₇ = \(\frac{7}{2}\) [2a + (n – 1)d] = 49
= 7[2a + (7 – 1) d] = 98
2a + 6d = \(\frac{98}{7}\) = 14
a + 3d = 7 → (1)
Sum of first 17 terms
S₁₇ = 289
\(\frac{n}{2}\) [2a + (n – 1)d] = 289
\(\frac{17}{2}\)[2a + (17 – 1)d] = 289
\(\frac{17}{2}\) [2a + 16d] = 289
2a + 16d = 289 × \(\frac{2}{17}\)
2a + 16d = 34
a + 8d = 17 → (2)
Solving equation (1) & (2) by eliminating method

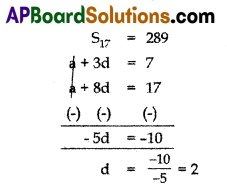
Substitute d = 2 in equation (1)
a + 3(2) = 7
a + 6 = 7
a = 7 – 6 = 1
Sum of first n terms
a + 3(2) =7
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S_n = \(\frac{n}{2}\)[2 × 1 + (n – 1)2]
= \(\frac{n}{2}\)[2 + 2n – 2]
S_n = \(\frac{n}{2}\) × 2n = n².

Question 14.
In a competitive exam, 3 marks are to be awarded for every correct answer and for every wrong answer, 1
mark will be deducted. Madhu scored 40 marks in this exam. Had 4 marks been awarded for each correct answer and 2 marks deducted for each incorrect answer,Madhu would have scored 50 marks. How many questions were there in the test? (Madhu attempted all the questions)
Answer:
Let the number of correct answers be x; and the number of wrong answers be y. When 3 marks are given for each correct answer and 1 mark deducted for each wrong answer, his score is 40 marks.
3x – y = 40 ………….. (1) His score would have been 50 marks if 4 marks were given for each correct answer and 2 marks deducted for each wrong answer. 4x – 2y = 50 ………….. (2)
Substitution method from equation (1),
y = 3x – 40 substitute in equation (2)
4x – 2 (3x – 40) = 50
4x – 6x + 80 = 50
– 2x = 50 – 80 = – 30
x = -30/-2
= 15
Substitute the value of x in equation (1) : 3(15)
-y = 40 ⇒ 45 – y = 40 ⇒ v =45 – 40 = 5
Total number of questions = x + y
= 15 + 5 = 20

Question 15.
Draw a circle of radius 6cm. From a point 10 cm away from its centre, construct tire pair of tangents to the circle and measure their lengths. Verify by using Pythagoras Theorem.
Answer:

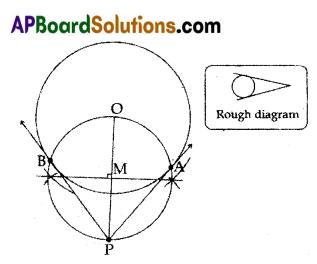
Steps of construction:
i) Let the centre of the given circle ‘O’ and ‘P’ be an external point Join PO and draw the perpendicular bisector of PO, which cuts it at the mid point M,
ii) Taking M as centre with radius PM or MO, we draw a circle that intersects the given circle at two points A and B.
iii) Join PA and PB. These are the required tangents of the circle.
Proof : From the figure, PO = 10 cm, OA = 6 cm.
Also ΔPOA is a right angled triangle.
By Pythagoras theorem,
PO² = PA² + OA² ⇒
PA² = PO² – OA² = 10² – 6² = 100 – 36 = 64
∴ PA = \(\sqrt{64}\) = 8 cm
In ΔOPB, ∠OBP = 90°. OB = 6 cm,
OP = 10 cm.
By Pythagoras theorem
OP² = OB² + BP²
⇒ BP² = OP² – OB²
BP² = 10² – 6² = 100 – 36 = 64
BP = \(\sqrt{64}\) = 8 cm.

Question 16.
Draw the graph for the polynomial p(x) = x² + 3x – 4 and hence find the zeroes from the graph.
Answer:
p(x) = x² + 3x – 4

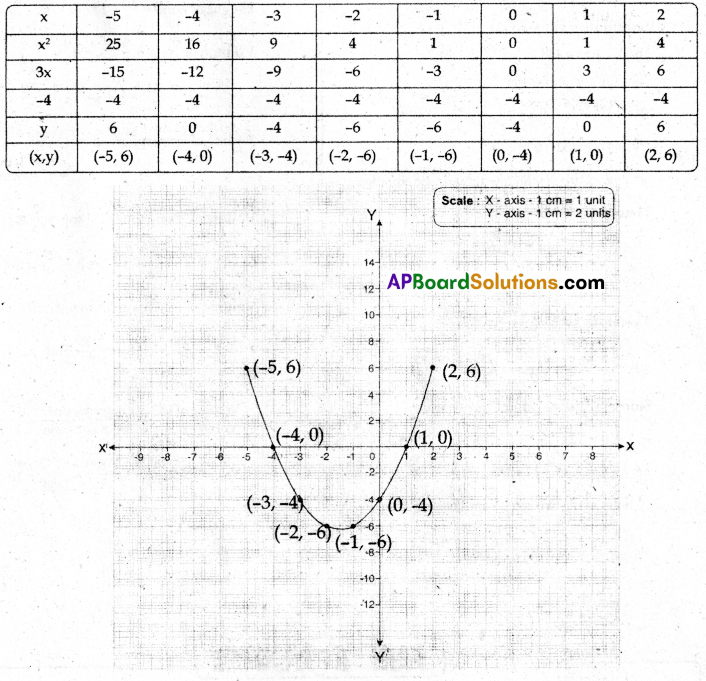
Zeroes of the given polynomial are -4, 1.

Question 17.
Sum of the areas of two squares is 468 m². If the difference of their perimeters is 24m find the sides of two squares.
Answer:
Let the sides of two squares be xm and ym.
Area of the first square is x²sq.m
Area of the second square is y²sq.m
Sum of the areas of two squares is x² + y²
Given sum of the areas is 468
x² + y² = 468 ……… (1)
Perimeter of the first square = 4x m
Perimeter of the second square = 4ym
Difference of their perimeters = 24
4x – 4y = 24
x – y = 6
x = 6 + y …………… (2)
Substitute x value in (1)
(6 + y)² + y² = 468
36 + 12y + y² + y² = 468
2y² + 12y + 36 – 468 = 0
2y² + 12y – 432 = 0
y² + 6y -216 = 0 which is a quadratic equation.
Here a = 1; b = 6; c = -216.
b² – 4ac = (6)² – 4 × 1(216)
= 36 + 864 = 900
Therefore y = \(\frac{-6 \pm \sqrt{900}}{2 \times 1}=\frac{-6 \pm 30}{2}\)
y = \(\frac{-6+30}{2}\), y = \(\frac{-6-30}{2}\) = \(\frac{24}{2}\) = 12 = \(\frac{-36}{2}\) = -18
Side of a square cannot be negative
∴ y = 12
x = 6 + y ⇒ x = 6 + 12 = 18
∴ Sides of the two square are 12m and 18m.

Question 18.
A container shaped like a right circular cylinder having diameter 12 cm. and height 15 cm. is full of ice cream. The icecream is to be filled into cones of height 12 cm. and diameter 6 era., having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Answer:
Diameter of cylinder = d = 12 cm
⇒ Radius of the cylinder = \(\frac{d}{2}\) = \(\frac{12}{2}\) cm = 6 cm
Height of the cylinder = h = 15 cm
Volume of the cylinder = πr²h
= \(\frac{22}{7}\) × 6 × 6 × 15 = \(\frac{11880}{7}\) cm³
Diameter of each cone = d₁ = 6 cm
Radius of cone = r₁ = \(\frac{d_1}{2}\) = \(\frac{12}{2}\)cm = 3cm
Height of cone = h₁ = 12 cm
Volume of cone = \(\frac{1}{3}\). πr₁²h₁
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 12 = \(\frac{792}{7}\) cm³
Radius of hemispherical top of the cone = r₁ = 3cm
Volume of hemispherical top = \(\frac{2}{3}\) πr₁³
\(\frac{2}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 3 = \(\frac{396}{7}\) cm³
Volume of ice cream in one cone
= \(\frac{792}{7}\) = \(\frac{396}{7}\) = \(\frac{1188}{7}\) cm³
No of required cones
= \(\frac{\text { Volume of icecream in container }}{\text { Volume of icecream in one cone }}\)
= \(\frac{11880 / 7}{1188 / 7}\) = \(\frac{11880}{7}\) \(\frac{7}{1188}\) = 10

Part – B (20 Marks)

Note :

1. Answer all the questions,
2. Each question carries 1 mark,
3. Answers are to be written in Question paper only,
4. Marks will not be awarded in any case of over uniting, rewriting or erased answers.

Note : Write the capital letters (A, B, C, D) showing the correct answer for the following questions in the brackets provided against them.

Question 1.
If A ⊂B then A∪(B – A) =
A) A
B) B
C) Φ
D) µ
Answer:
B) B

Question 2.
If the points (a, 0) (0, b) and (1, 1) are collinear, then \(\frac{1}{a}\) + \(\frac{1}{b}\) = …………….
A) 0
B) 1
C) 2
D) -1
Answer:
B) 1

Question 3.
In which quadrant does the point (-3, -3) lie ?
A) Q₁
B) Q₂
C) Q₃
D) Q₄
Answer:
C) Q₃

Question 4.
The sum of first n terms of the series a, 3a, 5a, …………. is
A) na
B) (2 n – 1) a
C) n²a
D) n²a²
Answer:
C) n²a

Question 5.
No. of odd numbers between 0 and 50
A) 24
B) 25
C) 23
D) 26
Answer:
B) 25

Question 6.
The roots of the quadratic equation \(\frac{11}{3+x}\) = 4 (3 – x)m
A) ±\(\frac{1}{5}\)
B) ±\(\frac{5}{2}\)
C) ±2
D) ±5
Answer:
B) ±\(\frac{5}{2}\)

Question 7.
The quadratic equation whose one root is 3 + √5 is
A) x² – 6x + 4 = 0
B) x² – 6x – 4 = 0
C) x² + 6x + 4 = 0
D) x² + 6x + 5 = 0
Answer:
A) x² – 6x + 4 = 0

Question 8.
The pair of equations x = 0 and y = 0 represents
A) parallel
B) perpendicular

D) ↔
Answer:
B) perpendicular

Question 9.
If α, β are zeroes of p(x) = x² – 5x + k and α – β = 1, then the value of ‘k’ is
A) µ
B) -6
C) 6
D) 5
Answer:
C) 6

Question 10.
The rational number between √2 and √3 is
A) \(\frac{6}{5}\)
B) \(\frac{3}{4}\)
C) \(\frac{3}{2}\)
D) \(\frac{4}{5}\)
Answer:
C) \(\frac{3}{2}\)

Question 11.
A man goes 150 m towards East and then 200 m towards North. How far is he from the starting point ?
A) 250 m
B) 160 m
C) 180 m
D) 150 m
Answer:
A) 250 m

Question 12.
A parallelogram ABCD and a triangle ABC are on the same and between the same parallel lines. If the area of the triangle ABE is 20 cm², then area of parallelogram ABCD is ……………. cm².
A) 20
B) 16
C) 40
D) 90
Answer:
C) 40

Question 13.
The number of tangents that can be drawn to a circle is …………….
A) 1
B) 2
C) 0
D) infinite
Answer:
D) infinite

Question 14.
Two spheres are in the ratio 3 : 5, what is the ratio of their surface areas ?
A) 9 : 16
B) 9 : 25
C) 25: 9
D) 16 : 1
Answer:
B) 9 : 25

Question 15.
Tan θ = 3/4 , then \(\frac{1-\cos \theta}{1+\cos \theta}\) = …………..
A) 9
B) -1
C) \(\frac{1}{9}\)
D) -9
Answer:
C) \(\frac{1}{9}\)

Question 16.
The length of the shadow of a tower is equal to its height, then the angle of elevation of the sun is ……………
A) 45°
B) 70°
C) 60°
D) 90°
Answer:
A) 45°

Question 17.
Two or more events of an experiment, where occurrence of all other events are called …………………… events.
A) Mutual
B) Non-considerable
C) Mutually exclusive
D) Considerable
Answer:
C) Mutually exclusive

Question 18.
The probability of getting a perfect square number from the number 1 to 10 is ………………..
A) \(\frac{1}{10}\)
B) \(\frac{3}{11}\)
C) \(\frac{2}{5}\)
D) \(\frac{1}{5}\)
Answer:
D) \(\frac{1}{5}\)

Question 19.
The median of scores x₁, x₂ and 2x is 6 and x₁ < 2x < x₂ then x₁ = ……………
A) 7
B) 3
C) 13
D) 31
Answer:
B) 3

Question 20.
Which of the following is not a measure of central tendancy ?
A) Mean
B) Median
C) Mode
D) Range
Answer:
C) Mode