TS 10th Class Maths Model Paper Set 5 with Solutions

The strategic use of TS 10th Class Maths Model Papers Set 5 can significantly enhance a student’s problem-solving skills.

TS SSC Maths Model Paper Set 5 with Solutions

Time: 3 Hours
Maximum Marks: 80

General Instructions:

1. Answer all the questions under Part – A on a separate answer book.
2. Write the answers to the questions under Part – B on the question paper itself and attach it to the answer book of Part – A.

Part – A (60 Marks)
Section – I (6 × 2 = 12 Marks)

Note :

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 1.
Is x (2x + 3) = x² + 5 a Quadratic equation ? Justify.
Solution:
x (2x + 3) = x² + 5
2x² + 3x = x² + 5
2x² + 3x – x² – 5 = 0
x² + 3x – 5 = 0
It is in the form of a x² + bx + c = 0.
So, the given equation is a quadratic equation.

Question 2.
Find the distance between the points (sec θ, 0) and (0, tan θ), when θ = 45°.
Solution:
Given points A(sec θ, 0) and B (0, tan θ) If θ = 45°,
then A(sec 45°, 0) and B (0, tan 45°)
A(√2,0) and B(0, 1)
∴ Distance between A, B
= \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
AB = \(\sqrt{(0-\sqrt{2})^2+(1-0)^2}\)
= \(\sqrt{2+1}\) = √3 units.
∴ Distance between (sec 45°, 0) and (0, tan 45°), when θ = 45° is √3 units

Question 3.
The solutions of the linear equation x + y = 8 are (1, 7), (2, 6) and (3, 5). The solutions of another linear equation 3x + 3y = 12 are (1, 3), (3, 1) and (0, 4). Plot these points on a graph sheet and draw lines.
Solution:

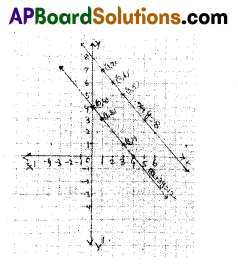
Question 4.
If the ratio of base radii of two right circular cylinder is 1 : 2 and the ratio of their heights is 2 : 3, then find the ratio of their volumes.
Solution:

∴ V₁ : V₂ = 1 : 6
∴ The ratio of the volumes of two cylinders = 1 : 6

Question 5.
In the given figure, if \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{2}{3}\), AE = 6 cm and AC = 15 cm, then is DE || BC ? Justify.

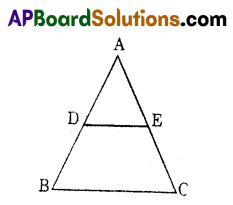
Solution:
Given \(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{2}{3}\),
AE = 6, and AC =15
∴ EC = AC – AE = 15 – 6 = 9
Now \(\frac{\mathrm{AE}}{\mathrm{EC}}\) = \(\frac{6}{9}\) = \(\frac{2}{3}\)
\(\frac{\mathrm{AD}}{\mathrm{DB}}\) = \(\frac{\mathrm{AE}}{\mathrm{EC}}\)
(By converse of BPT)
∴ DE//BC.

Question 6.
A circle is inscribed in ΔABC touching the sides AB, BC and CA at points D, E and F respectively. If AD = 3 cm, BE = 4 cm, CF = 5 cm, then find the perimeter of the triangle.

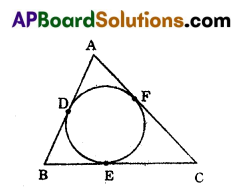
Solution:
Given AD = 3 cm, BE = 4 cm, CF = 5 cm AD = AF = 3 cm
BD = BE = 4 cm [Lengths of tan gents are equal]
CF = AF = 5 cm
∴ AB = AD + BD = 3 + 4 = 7 cm
BC = BE + EC = 4 + 5 = 9 cm
AC = AF + FC = 3 + 5 = 8 cm
∴ Perimeter of the
ΔABC = 7 + 9 + 8= 24 cm

Section – II (6 × 3 = 18 Marks)

 

Note :

1. Answer ALL the following questions.
2. Each question carries 2 marks.

Question 7.
Solve : 3x + 2y = 11 and 2x + 3y = 4.
Solution:
3x + 2y = 11 ……….. (1)
2x + 3y = 4 …………. (2)

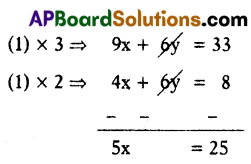
∴ x = \(\frac{25}{5}\) = 5
Substitute x = 5 in (1)
3(5) + 2y = 11
15 + 2y = 11
2y = 11 – 15
2y = -4
y = \(\frac{-4}{2}\) = -2
∴ Solution x = 5, y = -2

Question 8.
3, 6, 9, 12, ….. is an arithmetic progression. Find the sum of first 20 terms of the progression.
Solution:
Given A.P 3, 6, 9, 12, ……….
a = 3, d = a₂ – a₁ = 6 – 3 = 3, n = 20 S_n = ?
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
∴ Sum of 20 terms
S₂₀ = \(\frac{20}{2}\) [2(3) + (20 – 1)3]
= 10 [6 + 57] = 10 × 63 = 630
∴ Sum of 20 terms S₂₀ = 630.

Question 9.
If A = {4, 8, 12, 16, 20},
B = {6, 12, 18, 24, 30}, then show that n(A∪B) = n(A) + n(B) – n(A∩B).
Solution:
A = {4, 8, 12, 16, 20},
B = {6, 12, 18, 24, 30}
n(A) = 5, n(B) = 5
A∪B = {4, 8, 12, 16, 20}∪{6, 12, 18, 24, 30} = {4, 6, 8, 12, 16, 18, 20, 24, 30}
n(A∪B) = 9
A∩B = {4, 8, 12, 16, 20} ∩{6, 12, 18, 24, 30} = {12}
n(A∩B) = 1
n(A) + n(B) – n(A∩B)
= 5 + 5 – 1 = 10 – 1 = 9 = n(A∩B)
∴ n(A∪B) = n(A) + n(B) – n(A∩B)

Question 10.
Write the formula for median of a grouped data and explain each term of it.
Solution:
Median = l + \(\left[\frac{\frac{n}{2}-c f}{f}\right]\) × h
where,
l – lower boundary of median class.
n – number of observations.
cf – cumulative frequency of class preceding the median class.
f – frequency of median class.
h – size of the median class.

Question 11.
A bag contains 5 red, 8 white, 4 green colour balls. If a ball is selected randomly from the bag, then find the probability that selected ball is (i) a green ball, (ii) not a white ball.
Solution:
Red colour balls n(R) = 5
White colour balls n(W) = 8
Green colour balls n(G) = 4
∴ Total balls = 17
∴ The number of all possible outcomes n(S) = 17

i) The number of favourable outcomes to selected a green ball n(G) = 4
∴ P(G) = \(\frac{\mathrm{n}(\mathrm{G})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{4}{17}\)

ii) The number of favourable outcomes to selected not a white ball
= n((\(\overline{\mathbf{W}}\))) = 5 + 4 = 9
P((\(\overline{\mathbf{W}}\))) = \(\frac{\mathrm{n}(\overline{\mathrm{W}})}{\mathrm{n}(\mathrm{S})}\) = \(\frac{9}{17}\)

Question 12.
The statue stands on the top of a 3 metre tall pedestal. From a point on the ground angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the statue.
Solution:

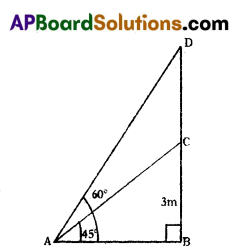
BC = Height of the pedestal = 3m
DC = Height of the statue
In ΔABC,
Tan 45° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
1 = \(\frac{3}{\mathrm{AB}}\)
∴ AB = 3 m
In ΔABD,
Tan 60° = \(\frac{\mathrm{BD}}{\mathrm{AB}}\) ⇒ 3 = \(\)
∴ BD = 3√3
3 + CD = 3
CD = 3√3 – 3
3(√3 – 1) = 3(1.732 – 1)
= 3 × 0.732 = 2.196 m
∴ Height of the statue CD = 2.196 m

Section – III (6 × 5 = 30 Marks)

Note :

1. Answer all the following questions.
2. In this section, every question has internal choice. Answer any one alternative.
3. Each question carries 5 marks.

Question 13.
A) Find the mode for the following data.

Solution:


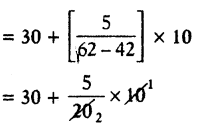
= 30 + 2.5 = 32.5
∴ Mode of the given data = 32.5

(OR)

B) A man observes top of a tower at an angle of elevation of 30°. When he walked 40 m towards the tower, the angle of elevation is changed to 60° Find the height of the tower and dis-tance from the first observation point to the tower.
Solution:
Given height of the tower we will find BC = 40 m; CD = x m

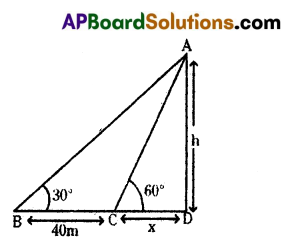
From figure tan 30° = \(\frac{h}{x+40}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{x+40}\)
x + 40 = √3h
x = √3h – 40 ………….. (1)
tan 60° = \(\frac{h}{x}\)
√3 = \(\frac{h}{\sqrt{3} h-40}\) [∵ from (1)]
3h – 40√3 = h
2h = 40√3 ⇒ h = 20√3 m
∴ Height of the tower = 20√3 m.
x = √3h – 40 = √3 × 20√3 – 40
= 3 × 20 -40 = 60 – 40 = 20m.
Distance from the first observation point to the tower.
BD = x + 40 = 20 + 40 = 60m.

Question 14.
A)Prove that √3 + √7 is an irrational number.
Solution:
Let us assume that √3 + √7 is a rational number.
Lut us √3 + √7 = \(\frac{\mathrm{a}}{\mathrm{b}}\), where a, b are coprimes and b ≠ 0
∴ √7 = \(\frac{\mathrm{a}}{\mathrm{b}}\) – √3
(√7)² = (\(\frac{\mathrm{a}}{\mathrm{b}}\) – √3)² (S.O.B.S)
7 = \(\frac{a^2}{b^2}\) – 2\(\frac{\mathrm{a}}{\mathrm{b}}\)√3 + 3
2\(\frac{\mathrm{a}}{\mathrm{b}}\)√3 = \(\frac{a^2}{b^2}\) + 3 – 7
2\(\frac{\mathrm{a}}{\mathrm{b}}\)√3 = \(\frac{a^2}{b^2}\) – 4
⇒ √3 = \(\frac{a^2-4 b^2}{b^2} \times \frac{b}{2 a}\)
∴ √3 = \(\frac{a^2-4 b^2}{2 a b}\)
Since, a, b are integers \(\frac{a^2-4 b^2}{2 a b}\) is a rational number.
So, √3 is also a rational number.
This contradicts the fact that √3 is irrational number.
Hence √3+ √7 is an irrational number.

(OR)

B) Prove that \(\frac{1+\sin \theta}{\cos \theta}+\frac{\cos \theta}{1+\sin \theta}\) = 2 sec θ.
Solution:
LHS = \(\frac{1+\sin \theta}{\cos \theta}+\frac{\cos \theta}{1+\sin \theta}\)


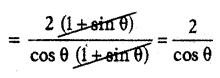
= 2 sec θ = RHS
∴ LHS = RHS

Question 15.
A) From the given Venn-diagram, write the sets A∪B, A∩B, A – B and B – A.

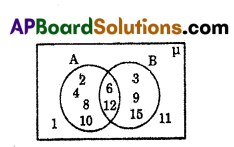
Solution:
i) A∪B = {2, 3, 4, 6, 8, 9, 10, 12, 15}
ii) A∩B = {6, 12}
iii) A – B = {2, 4, 8, 10}
iv) B – A = {3, 9, 15}

(OR)

B) A metallic vessel is in the shape of a right circular cylinder mounted over a hemisphere. The common diameter is 42 cm and the height of the cylindrical part is 21 cm. Find the capacity of the vessel. (Take π = \(\frac{22}{7}\))
Solution:
Common diameter of the cylinder and hemisphere d = 42 cm.
Common radii r = 21 cm
Height of the cylinder h = 21 cm.

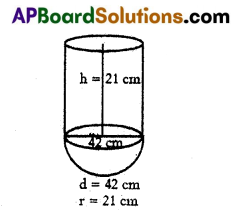
∴ Capacity of the vessel = Volume of cylinder + Volume of Hemisphere.
= πr²h + \(\frac{2}{3}\)πr³
= \(\frac{22}{7}\)(21)² × 21 × \(\frac{2}{3}\) × \(\frac{22}{7}\) (21)³
= \(\frac{22}{7}\) × 21³[1 + \(\frac{2}{3}\)]
= \(\frac{22}{7}\) × 21³ × \(\frac{5}{3}\) = \(\frac{22 \times 21^3 \times 5}{21}\)
= 22 × 21² × 5 = 48,510 cm³
∴ Capacity of the vessel = 48,510 cm³

Question 16.
A) A train travels 360 km at a uniform speed. If the speed had been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
The distance travelled = 360 km
Let the speed of the train = x kmph
Time taken to complete a journey = \(\frac{\text { distance }}{\text { speed }}\)
By problem (\(\frac{360}{x}-\frac{360}{x+5}\)) = 1
360(\(\frac{1}{x}-\frac{1}{x+5}\)) = 1
360(\(\frac{x+5-x}{x(x+5)}\)) = 1
\(\frac{5}{x^2+5 x}=\frac{11}{360}\)
x² + 5x = 1800
x + 5x – 1800 = 0
x + 45x – 40x – 1800 = 0
x (x + 45) – 40 (x + 45) = 0
(x + 45) (x – 40) = 0
x + 45 = 0 (or) x – 40 = 0
x = -45 or x = + 40
But x can’t be negative.
∴ The speed of the train = 40 kmph

(OR)

B) Show that the distance of the points (5, 12), (7, 24) and (35, 12) from the origin are arranged in the ascending order, forms an arithmetic progression, Find the common difference of the progression.
Solution:
i) Distance of the point (5, 12) from the origin (0, 0)
∴ Distance of the point (x, y) from origin (0, 0) = \(\sqrt{x^2+y^2}\)
= \(\sqrt{5^2+12^2}\) = \(\sqrt{25+144}\) = \(\sqrt{169}\)
= 13 units.

ii) Distance of the point (7, 24) from the origin (0, 0)
= \(\sqrt{7^2+24^2}\) = \(\sqrt{49+576}\)
= \(\sqrt{625}\) = 25 units.

iii) Distance of the point (35, 12) from the origin (0, 0)
= \(\sqrt{35^2+12^2}\) = \(\sqrt{1225+144}\)
= \(\sqrt{1369}\) = 37 units.
Above distance in ascending order.
13, 25, 37
a₁, a₂, a₃
a₂ – a₁ = 25 – 13 = 12
a₃ – a₂ = 37 – 25 = 12
a₂ – a₁ = a₃ – a₂
∴ 13, 25, 37 are in an A.P
Common difference d = a₂ – a₁ = 12

Question 17.
A) Draw the graph of the polynomial P(x) = x² – x – 2 and find the zeroes of the polynomial from the graph.
Solution:
Let y = x² – x – 2

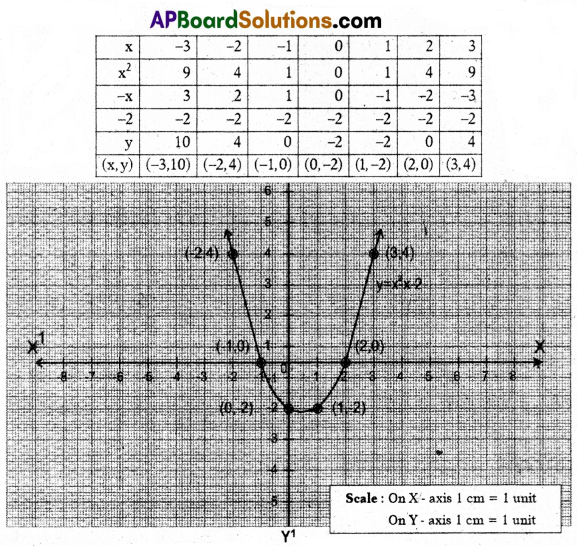
∴ Zeroes of the polynomial are 2, -1

(OR)

B) Draw the graph of x + y = 11 and x – y = 5. Find the solution of the pair of linear equations.
Solution:
Given x + y = 11 and x – y = 5
a₁x + b₁y + c₁ = 0; a₂x + b₂y + c₂ = 0
\(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) = \(\frac{1}{1}\); \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\) = \(\frac{1}{-1}\) ∴ \(\frac{\mathrm{a}_1}{\mathrm{a}_2}\) ≠ \(\frac{\mathrm{b}_1}{\mathrm{b}_2}\)
Hence the linear equations are consistent.

x + y = 11
x	y	(x, y)
0	11	(0, 11)
11	0	(11, 0)

x – y = 5
x	y	(x, y)
0	-5	(0, -5)
5	0	(5, 0)

∴ The lines intersecting at a point (8, 3)

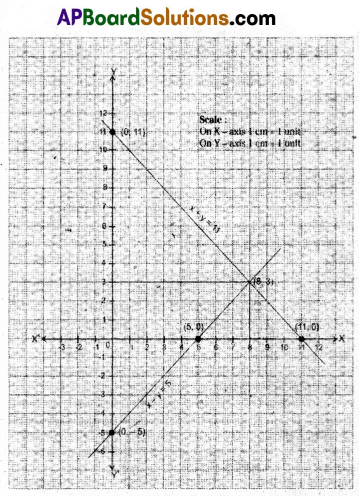
Check Method: Intersect at a point (8, 3)
x + y = 11
8 + 3 = 11
11 = 11

x – y = 5
8 – 3 = 5
5 = 5

Question 18.
A) Draw a circle of radius 4 cm. from a point 9 cm away from it’s centre, construct a pair of tangents to the circle.

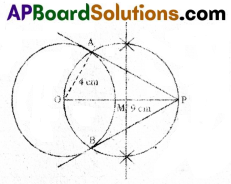
Solution:
OA = 4 cm, OP = 9 cm

Steps of construction:

1. Draw a circle with a radius 4 cm and “O” as centre.
2. Take a point such that OP = 9 cm. Join OP.
3. Draw a perpendicular bisector to OP which is bisects OP at M.
4. Draw a circle M as centre and PM as radius.
5. Let the circle intersects the given circle at ‘A’ and ‘B’,
6. Join P to A and B.
7. PA, PB are the required pair of tan-gents.

(OR)

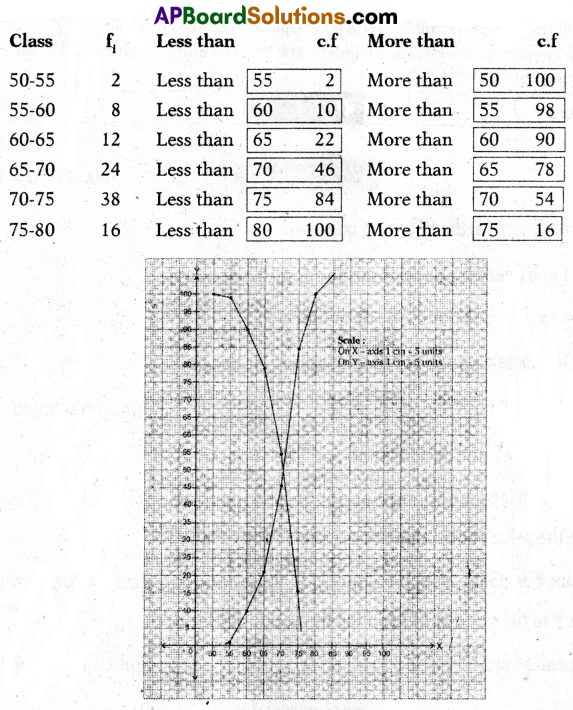
B) The following table gives the marks obtained by 100 students in SA – 1 exams in Mathematics subject.
Draw Ogive graph of less than and greater than.

Solution:
The given data is to be changed to more than frequency distribution type.

Part – B (20 Marks)

Note :

1. Answer all the questions.
2. Each question carries 1 mark.
3. Answers are to be written in the Question paper only.
4. Marks will not be awarded in any case of over writing, rewriting or erased answers.

Note : Write the capital letters (A, B, C, D) showing the correct answer for the following questions in the brackets provided against them. (Marks : 20 × 1 = 20)

Question 1.
If A = {x : x is a day of a week}, then the value of n(A) is …………..
A) 6
B) 4
C) 5
D) 7
Answer:
D) 7

Question 2.
The degree erf the polynomial p(x) = 3x³ + 0.x⁴ + 0x – 2x² + 4 is …………
A) 1
B) 2
C) 3
D) 4
Answer:
C) 3

Question 3.
The midpoint of the line segment joining the points (3, 5), (x, 3) is (4, 4), then the value of x is …………..
A) 3
B) 4
C) 5
D) 7
Answer:
C) 5

Question 4.
The decimal form of \(\frac{3}{4}\) is …………….
A) 0.75
B) 0.50
C) 0.25
D) 0.075
Answer:
A) 0.75

Question 5.
If 3x + 2y = 6, 9x + ky = 7 represents two inconsistent equations, then the value of k is ………………
A) 5
B) 6
C) 8
D) 7
Answer:
B) 6

Question 6.
The total cost of 4 pencils and 5 note books is Rs.180. The linear equation representing this data is …………….
A) x + y = 180
B) 4x + 5y = 180
C) 9x + y = 180
D) 4x + 5y = 20
Answer:
B) 4x + 5y = 180

Question 7.
If the sum of first n terms of an arithmetic progression is \(\frac{n^2+n}{2}\), then the sum of first 10 terms is ………………….
A) 55
B) 110
C) 50
D) 45
Answer:
A) 55

Question 8.
The sum of the roots of the Quadratic equation 2x² + 6x + 4 = 0 is ………………
A) 3
B) -3
C) 2
D) -2
Answer:
B) -3

Question 9.
The nature of roots of the Quadratic equation x² + 10x + 24 = 0 is ……………
A) Real and distinct.
B) Real and equal.
C) No real roots.
D) One root is positive and the other root is negative.
Answer:
A) Real and distinct.

Question 10.
In an arithmetic progression n^th term is a_n = a + (n – 1) d. In this formula ‘d’ represents …………..
A) Number of terms
B) n^thterm
C) First term
D) Common difference
Answer:
D) Common difference

Question 11.
From the given Ogive curve, the value of the median of the data is …………….

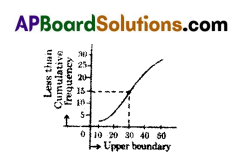
A) 20
B) 25
C) 15
D) 30
Answer:
D) 30

Question 12.
The curved surface area of a right circular cone is CSA = πrl. In this ‘l’ represents ………………..
A) Height
B) Radius
C) Slant height
D) Diameter
Answer:
C) Slant height

Question 13.
Among the following, the value which is not possible for the probability of an event is …………….
A) \(\frac{1}{3}\)
B) 0.5
C) 25%
D) \(\frac{4}{3}\)
Answer:
D) \(\frac{4}{3}\)

Question 14.
In ΔABC, DE || BC, AD = 6 cm, DB = 2 cm, DE = 9 cm and BC = x cm, then the value of x ,is ……………..

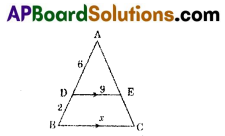
A) 6
B) 8
C) 9
D) 12
Answer:
D) 12

Question 15.
In the given figure, PA and PB are tangents drawn to the circle and AB is a chord. If PA = 6 cm and ∠PAB = 60°, then the length of the chord AB is ……………..

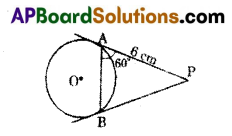
A) 5 cm
B) 6 cm
C) 7 cm
D) 4 cm
Answer:
B) 6 cm

Question 16.
In ΔABC, ∠B = 90°, AB = 100 cm and BC = 100 √3 cm, then the value of angle θ is ……………

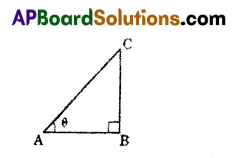
A) 30°
B) 60°
C) 45°
D) 25°
Answer:
B) 60°

Question 17.
If θ = 45°, then the value of \(\frac{1-\cos 2 \theta}{\sin 2 \theta}[latex] is …………….
A) 2
B) infinity
C) 1
D) 0
Answer:
C) 1

Question 18.
If one letter is selected randomly from the letters of the word “EXAMINATION”, then the probability of getting a vowel is …………..
A) [latex]\frac{5}{12}\)
B) \(\frac{6}{11}\)
C) \(\frac{4}{9}\)
D) \(\frac{5}{11}\)
Answer:
B) \(\frac{6}{11}\)

Question 19.
Which of the following is not true?
A) sin θ = \(\sqrt{1-\cos ^2 \theta}\)
B) sec²θ – tan²θ = 1
C) cos θ • cosec θ = 1
D) tan θ • cot θ = 1
Answer:
C) cos θ • cosec θ = 1

Question 20.
In the given figure, ‘O’ is the centre of the circle, OA and OB are radii. PA and PB are the tangents to the circle at points A and B. If ∠AOB = 120°, then the value of ∠APB is ……………

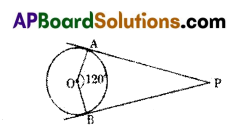
A) 60°
B) 30°
C) 90°
D) 45°
Answer:
A) 60°