AP Inter 2nd Year Maths 2A Question Paper May 2019

Thoroughly analyzing AP Inter 2nd Year Maths 2A Model Papers and AP Inter 2nd Year Maths 2A Question Paper May 2019 helps students identify their strengths and weaknesses.

AP Inter 2nd Year Maths 2A Question Paper May 2019

Time: 3 Hours
Maximum Marks: 75

Note: This question paper consists of THREE sections A, B, and C.

Section – A
(10 × 2 = 20 Marks)

I. Very Short Answer Type Questions.

• Answer ALL questions.
• Each question carries TWO marks.

Question 1.
Find the multiplicative inverse of 7 + 24i.
Solution:
The multiplicative inverse of a + ib is \(\frac{a}{a^2+b^2}-i \frac{b}{a^2+b^2}\)
∴ The multiplicative inverse of 7 + 24i is

Question 2.
Simplify i² + i⁴ + i⁶ + …….. up to (2n + 1) terms.
Solution:
i² + i⁴ + i⁶ + ………(2n + 1) terms
= i² + (i²)² + (i²)³ + ……….(2n + 1) terms
= -1 + (-1)² + (-1)³ + (-1)⁴ + ………(2n + 1) terms
= -1 + 1 – 1 + 1 – ………(2n + 1) terms
= -1
∴ i² + i⁴ + i⁶ + ……….(2n + 1) terms = -1.

Question 3.
If x = cis θ, then find the value of x⁶ + \(\frac{1}{x^6}\).
Solution:
x = cis θ = cos θ + i sin θ
∴ x⁶ = (cos θ + i sin θ)⁶ = cos 6θ + i sin 6θ
\(\frac{1}{x^6}=\frac{1}{\cos 6 \theta+i \sin 6 \theta}\) = cos 6θ – i sin 6θ
∴ x⁶ + \(\frac{1}{x^6}\) = cos 6θ + i sin 6θ + cos 6θ – i sin 6θ
∴ x⁶ + \(\frac{1}{x^6}\) = 2 cos 6θ

Question 4.
Form the quadratic equation whose roots are \(\frac{p-1}{p+q}\) and \(\frac{-(p+q)}{p-q}\) (p ≠ ±q).
Solution:

Question 5.
Find the algebraic equation whose roots are 2 times the roots of x⁵ – 2x⁴ + 3x³ – 2x² + 4x + 3 = 0.
Solution:
Let f(x) = x⁵ – 2x⁴ + 3x³ – 2x² + 4x + 3
The algebraic equation whose roots are 2 times the roots of f(x) = 0 is f(\(\frac{x}{2}\)) = 0.

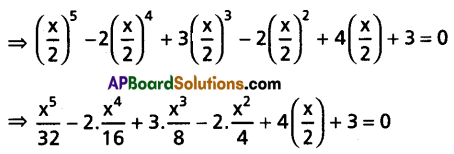
⇒ x⁵ – 4x⁴ + 12x³ – 16x² + 64x + 96 = 0.

Question 6.
Find the number of functions from a set A containing 5 elements into a set B containing 4 elements.
Solution:
Here n(A) = 5 and n(B) = 4
The number of functions from a set A into a set B is [n(B)]^n(A).
∴ The number of functions from set A into a set B is 4⁵.

Question 7.
If ¹⁵C_2r-1 = ¹⁵C_2r+4, find r.
Solution:
Given ¹⁵C_2r-1 = ¹⁵C_2r+4
⇒ 15 = 2r – 1 + 2r + 4
⇒ 15 = 4r + 3
⇒ 4r = 12
⇒ r = 3

Question 8.
If ²²C_r is the largest binomial coefficient in the expansion of (1 + x)²², find the value of ¹³C_r.
Solution:
Here n = 22 (even integer)
∴ Largest binomial co-efficient = \({ }^{\mathrm{n}} \mathrm{C}_{\left(\frac{\mathrm{n}}{2}\right)}\) = ²²C₁₁
∴ r = 11
∴ ¹³C_r = ¹³C₁₁
= ¹³C₂
= \(\frac{13 \times 12}{2}\)
= 78

Question 9.
Find the mean deviation from the mean of the following discrete data:
6, 7, 10, 12, 13, 4, 12, 16
Solution:
The arithmetic mean of the given data is
\(\bar{S}\) = \(\frac{6+7+10+12+13+4+12+16}{8}\)
= \(\frac{80}{8}\)
= 10
∴ Absolute values about mean = |6 – 10|, |7 – 10|, |10 – 10|, |10 – 12|, |10 – 13|, |10 – 4|, |10 – 12|, |10 – 16| = 4, 3, 0, 2, 3, 6, 2, 6
∴ Mean deviation = \(\frac{4+3+0+2+3+6+2+6}{8}\)
= \(\frac{26}{8}\)
= 3.25

Question 10.
For a binomial distribution with mean 6 and variance 2, find the first two terms of the distribution.
Solution:
Mean, np = 6
Variance, npq = 2
∴ \(\frac{n p q}{n p}=\frac{2}{6}=\frac{1}{3}\)
⇒ q = \(\frac{1}{3}\)
∴ p = 1 – q
= 1 – \(\frac{1}{3}\)
= \(\frac{2}{3}\)
∴ n(\(\frac{2}{3}\)) = 6
⇒ n = 9

Section – B
(5 × 4 = 20 Marks)

II. Short Answer Type Questions.

• Answer ANY FIVE questions.
• Each question carries FOUR marks.

Question 11.
If the real part of \(\left(\frac{z+1}{z+i}\right)\) is 1, then find the locus of z where z = x + iy.
Solution:
Given z = x + iy

Since real part of \(\left(\frac{z+1}{z+i}\right)\) is 1
∴ \(\frac{x(x+1)+y(y+1)}{x^2+(y+1)^2}\) = 1
⇒ x² + x + y² + y = x² + y² + 2y + 1
⇒ x – y – 1 = 0
∴ The locus of z is x – y – 1 = 0.

Question 12.
Prove that \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4, if x is real.
Solution:

⇒ 3yx² + 4yx + 4 = 4x + 1
⇒ 3yx² + (4y – 4)x + (y – 1) = 0
x ∈ R ⇒ (4y – 4)² – 4(3y) (y – 1) ≥ 0
⇒ 16y² – 32y + 16 – 12y² + 12y ≥ 0
⇒ 4y² – 20y + 16 ≥ 0
⇒ 4y² – 20y +16 = 0
⇒ y² – 5y + 4 = 0
⇒ (y – 1) (y – 14) = 0
⇒ y = 1, 4
⇒ 4y² – 20y +16 ≥ 0
⇒ y ≤ 1 (or) y ≥ 4
⇒ y does not lie between 1 and 4.
Since the y² coefficient the exp ≥ 0.
∴ \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4.

Question 13.
Find the number of 4-letter words that can be formed using the letters of the word MIRACLE. How many of them:
(i) Begin with a vowel
(ii) Begin and end with vowels
(iii) End with a consonant.
Solution:
The word MIRACLE has 7 letters with 3 vowels (I, A, E) and 4 consonants (M, R, C, L).
The No.of 4-letter words that can be formed by using these letters is ⁷p₄
= 7 × 6 × 5 × 4
= 840

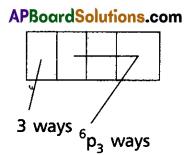
(i) For the required arrangements first place can be filled in 3 ways and the remaining three places can be filled with the remaining 6 letters it can be done in ⁶p₃ ways.
∴ The no.of 4 letter words that are begin with vowel = 3 × ⁶p₃
= 3 × 6 × 5 × 4
= 360
(ii) For the required arrangement first and last places can be filled with ³p₂ ways and the remaining two places can be filled remaining 5 letters it can done in ⁵p₂ ways.
∴ The no.of 4-letter words that begin and end with a vowel is ³p₂ × ⁵p₂
= 3 × 2 × 5 × 4
= 120

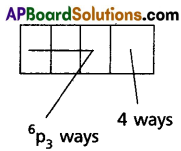
(iii) For the required arrangement, first we can fill the last place it can be done in 4 ways.
The remaining three places can be filled with the remaining 6 letters it can be done in ⁶p₃ ways.
∴ The no.of 4 letter words that are end with consonant = 4 × ⁶p₃
= 4 × 6 × 5 × 4
= 480

Question 14.
Prove that \(\frac{{ }^{4 n} C_{2 n}}{{ }^{2 n} C_n}=\frac{1.3 .5 \ldots \ldots . .(4 n-1)}{\{1 \cdot 3 \cdot 5 \ldots \ldots \ldots . .(2 n-1)\}^2}\).
Solution:

Question 15.
Resolve \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}\) into partial fractions.
Solution:
x⁴ + x² + 1 = x⁴ + 2x² + 1 – x²
= (x² + 1)² – x²
= (x² + 1 + x) (x² + 1 – x)
= (x² + x + 1) (x² – x + 1)
Let \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}=\frac{A x+B}{x^2+x+1}+\frac{C x+D}{x^2-x+1}\)
⇒ 3x³ – 2x² – 1 = (Ax + B) (x² – x + 1) + (Cx + D) (x² + x + 1)
Equating the coefficients of like terms, we have
A + C = 3 ………(1)
⇒ C = 3 – A
-A + B + C + D = -2 ………(2)
A – B + C + D = 0 ……….(3)
B + D = -1 ………(4)
⇒ D = -1 – B
Substitute C, D in (2)
-A + B + 3 – A – 1 – B = -2
⇒ -2A = -4
⇒ A = 2
∴ C = 3 – 2 = 1
Substitute C, D in (3)
A – B + 3 – A – 1 – B = 0
⇒ -2B = -2
⇒ B = 1
∴ D = -1 – 1 = -2
∴ A = 2, B = 1, C = 1, D = -2
∴ \(\frac{3 x^3-2 x^2-1}{x^4+x^2+1}=\frac{2 x+1}{x^2+x+1}+\frac{x-2}{x^2-x+1}\)

Question 16.
The probabilities of three mutually exclusive events are respectively given as \(\frac{1+3 P}{3}, \frac{1-P}{4}, \frac{1-2 P}{2}\). Prove that \(\frac{1}{3}\) ≤ P ≤ \(\frac{1}{2}\).
Solution:
∴ 0 ≤ \(\frac{1+3 p}{3}\) ≤ 1
⇒ 0 ≤ 1 + 3p ≤ 3
⇒ -1 ≤ 3p ≤ 2
⇒ \(\frac{-1}{3} \leq p \leq \frac{2}{3}\) …….(1)
∴ 0 ≤ \(\frac{1-p}{4}\) ≤ 1
⇒ 0 ≤ 1 – p ≤ 4
⇒ -1 ≤ -p ≤ 3
⇒ 1 ≥ p ≥ -3
⇒ -3 ≤ p ≤ 1 ……….(2)
∴ o ≤ \(\frac{1-2 p}{2}\) ≤ 1
⇒ 0 ≤ 1 – 2p ≤ 2
⇒ -1 ≤ – 2p ≤ 1
⇒ 1 ≥ 2p ≥ -1
⇒ -1 ≤ 2p ≤ 1
⇒ \(\frac{-1}{2} \leq p \leq \frac{1}{2}\) ………(3)
From (1), (2), (3) we have
\(\frac{1}{3} \leq p \leq \frac{1}{2} \Rightarrow p \in\left(\frac{1}{3}, \frac{1}{2}\right)\)

Question 17.
If A and B are independent events of a random experiment, show that A^C and B^C are also independent.
Solution:
Given A and B are independent events.
∴ P(A ∩ B) = P(A) . P(B)
P(A^C ∩ B^C) = P[(A ∪ B)^C]
= 1 – P(A ∪ B)
= 1 – [P(A) + P(B) – P(A ∩ B)]
= 1 – [P(A) + P(B) – P(A) + P(B)]
= 1 – P(A) – P(B) + P(A) . P(B)
= [1 – P(A)] – P(B) [1 – P(A)]
= [1 – P(A)] [1 – P(B)]
= P(A^C) . P(B^C)
∴ A^C and B^C are also independent.

Section – C
(5 × 7 = 35 Marks)

III. Long Answer Type Questions.

• Answer ANY FIVE questions.
• Each question carries SEVEN marks.

Question 18.
If α, β are the roots of the equation x² – 2x + 4 = 0, then for any n ∈ N show that \(\alpha^n+\beta^n=2^{n+1} \cos \left(\frac{n \pi}{3}\right)\).
Solution:

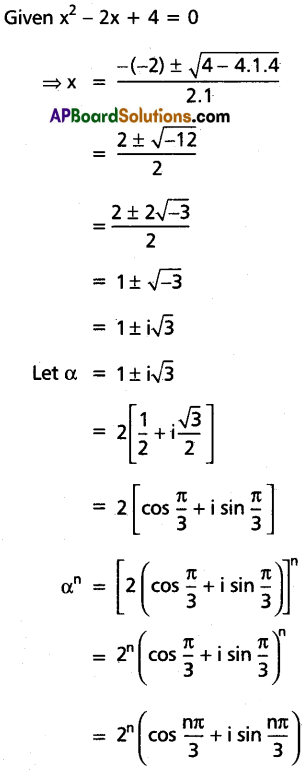
Question 19.
Find the polynomial equation whose roots are the translates of those of the equation x⁴ – 5x³ + 7x² – 17x + 11 = 0 by -2.
Solution:
Let f(x) ≡ x⁴ – 5x³ + 7x² – 17x + 11 = 0
The polynomial equation whose roots are translates of those of the equation f(x) = 0 by – 2 is f(x + 2) = 0
⇒ (x + 2)⁴ – 5(x + 2)³ + 7(x + 2)² – 17(x + 2) + 11 = 0

∴ Required equation is x⁴ + 3x³ + x² – 17x – 19 = 0.

Question 20.
If the coefficients of x⁹, x¹⁰, x¹¹ in the expansion of (1 + x)ⁿ are in A.P., then prove that n² – 41n + 398 = 0.
Solution:
The co-efficients of x⁹, x¹⁰, x¹¹ in the expansion of (1 + x)ⁿ are ⁿC₉, ⁿC₁₀, ⁿC₁₁.
Given that ⁿC₉, ⁿC₁₀, and ⁿC₁₁ are in A.P.
∴ ⁿC₉ + ⁿC₁₁ = 2 . ⁿC₁₀

⇒ \(\frac{110+n^2-10 n-9 n+90}{11(n-9)}\) = 2
⇒ n² – 19n + 200 = 22(n – 9)
⇒ n² – 19n + 200 = 22n – 198
⇒ n² – 41n + 398 = 0

Question 21.
If x = \(\frac{1.3}{3.6}+\frac{1 \cdot 3 \cdot 5}{3 \cdot 6 \cdot 9}+\frac{1 \cdot 3 \cdot 5 \cdot 7}{3 \cdot 6 \cdot 9 \cdot 12}+\)………, then prove that 9x² + 24x = 11.
Solution:



⇒ 4 + 3x = 3√3
⇒ (4 + 3x)² = 27
⇒ 16 + 9x² + 24x = 27
⇒ 9x² + 24x = 11

Question 22.
Find the mean deviation about the median for the following continuous distribution:

Marks Obtained	No. of Boys
0-10	6
10-20	8
20-30	14
30-40	16
40-50	4
50-60	2

Solution:
Construct the table

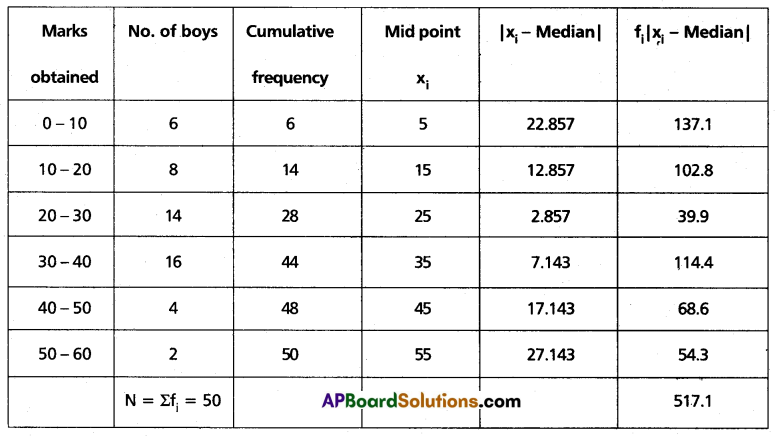
\(\frac{N}{2}=\frac{50}{2}\) = 25
∴ 20 – 30 is the median class.
∴ Median = L + \(\left(\frac{\frac{N}{2}-\text { Preceding cumulative Frequency }}{f}\right) i\)
= 20 + \(\left(\frac{25-14}{14}\right)\)10
= 20 + 7.857
= 27.857
∴ Mean deviation about median = \(\frac{1}{N} \sum_{i=1}^6 f_i\)|x_i – median|
= \(\frac{1}{50}\)(517.1)
= 10.34

Question 23.
Suppose an urn B₁ contains 2 white and 3 black balls and another urn B₂ contains 3 white and 4 black balls. One urn is selected at random and a ball is drawn from it. If the ball drawn is found to be black, find the probability that the urn chosen was B₁.
Solution:
Let E₁ and E₂ denote the events or selecting urns B₁ and B₂ respectively.
∴ P(E₁) = P(E₂) = \(\frac{1}{2}\)

Question 24.
A random variable X has the following probability distribution:

X = x	P(X = x)
0	0
1	k
2	2k
3	2k
4	3k
5	k2
6	2k2
7	7k2 + k

Find: (i) k (ii) the mean and (iii) P(0 < X < 5).
Solution:
We know P(X = x) = 1
⇒ P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + P(X = 5) + P(X = 6) + P(X = 7) = 1
⇒ 0 + k + 2k + 2k + 3k + k² + 2k² + 7k² + k = 1
⇒ 10k² + 9k = 1
⇒ 10k² + 9k – 1 = 0
⇒ 10k² + 10k – k – 1 = 0
⇒ 10k(k + 1) – 1(k + 1) = 0
⇒ (k + 1) (10k – 1) = 0
⇒ k = -1 (or) \(\frac{1}{10}\)
∴ k = \(\frac{1}{10}\) Since k > 0
(i) k = \(\frac{1}{10}\)

(ii) Mean = 0 (P = 0) + 1 P(X = 1) + 2 P(X = 2) + 3 P(X = 3) + 4 P(X = 4) + 5 P(X = 5) + 6 P(X = 6) + 7 P(X = 7)
= 0(0) + 1(k) + 2(2k) + 3(2k) + 4(3k) + 5(k²) + 6(2k²) + 7(7k² + k)
= 0 + k + 4k + 6k + 12k + 5k² + 12k² + 49k² + 7k
= 66k² + 30k
= \(66\left(\frac{1}{10}\right)^2+30\left(\frac{1}{10}\right)\)
= 66(\(\frac{1}{100}\)) + 3
= 0.66 + 3
= 3.66

(iii) P(0 < x < 5) = P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4)
= k + 2k + 2k + 3k
= 8k
= 8(\(\frac{1}{10}\))
= 0.8
∴ P(0 < x < 5) = 0.8.