AP Inter 1st Year Physics Important Questions Chapter 6 పని, శక్తి, సామర్ధ్యం

Students get through AP Inter 1st Year Physics Important Questions 6th Lesson పని, శక్తి, సామర్ధ్యం which are most likely to be asked in the exam.

AP Inter 1st Year Physics Important Questions 6th Lesson పని, శక్తి, సామర్ధ్యం

Very Short Answer Questions (అతిస్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
బలం వల్ల పని జరగని పరిస్థితులను తెలపండి. [Imp.Q][TS 15]
జవాబు:
పని W = \(\overline{\mathrm{F}}.\overline{\mathrm{S}}\) = |F||S|cos θ; θ = 90° అయితే cos90° = 0 ⇒ W = 0

1. బలం మరియు స్థానభ్రంశం పరస్పరం లంబంగా ఉన్నపుడు పని శూన్యమగును.
2. బలం పనిచేసినపుడు స్థానభ్రంశం శూన్యమైనపుడు కూడా పని శూన్యమగును.

ప్రశ్న 2.
పని, శక్తి, సామర్థ్యాలను నిర్వచించండి. వాటి SI ప్రమాణాలు తెలపండి. [Imp.Q]
జవాబు:
పని (W) :
ఒక వస్తువుపై స్థిరబలం పనిచేసినప్పుడు, ఆ వస్తువు బలం దిశలో స్థానభ్రంశం చెందితే అక్కడ పని జరిగింది అంటాం.
SI ప్రమాణం: 1 జౌల్ (J)

శక్తి : పని చేయగల ధారుడ్యాన్ని లేదా స్తోమతను శక్తి అంటారు.
SI ప్రమాణం-జౌల్; CGS ప్రమాణం – ఎర్గ్

సామర్ధ్యం (P) :
ఒక బలం వల్ల జరిగిన పని రేటును సామర్ధ్యం అని అంటారు. సామర్ధ్యం (P) = కాలం
SI ప్రమాణం : వాట్ (W) (లేదా) జౌల్ / సెకను; CGS ప్రమాణం : ఎర్గ్ / సెకను

ప్రశ్న 3.
గతిజశక్తి మరియు ద్రవ్యవేగాల మధ్య సంబంధాన్ని వ్రాయండి. [Imp.Q]
జవాబు:

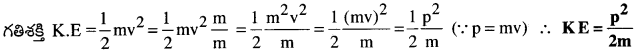
ప్రశ్న 4.
ఈ క్రింది సందర్భాలలో ఒక బలం చేసిన పని సంజ్ఞను తెలియచేయండి.
a) బకెటు బిగించిన తాడు సహాయంతో బావిలో నుంచి బకెట్ను తీసే సందర్భంలో మనిషి చేసిన పని
b) పై సందర్భంలో గురుత్వబలం చేసిన పని
జవాబు:
a) బావిలో నుండి బొక్కెనను పైకి లాగుచున్నపుడు మనిషి ప్రయోగించిన బలం, బొక్కెన స్థానభ్రంశము రెండూ పై వైపునకు ఉండును. కావున మనిషి చేసిన పని ధనాత్మకం.

b) బొక్కెనపై పని చేయు గురుత్వాకర్షణ బలం క్రింది దిశలో ఉండును. బొక్కెన స్థానభ్రంశం పై దిశలో ఉండును. కావున గురుత్వాకర్షణ బలం వలన జరిగిన పని ఋణాత్మకం.

ప్రశ్న 5.
ఈ క్రింది సందర్భాలలో ఒక బలం చేసిన పని సంజ్ఞను తెలియచేయండి.
a) ఒక వస్తువు వాలు తలంపై క్రిందికి జారుతున్నప్పుడు ఘర్షణ చేసిన పని
b) పై సందర్భంలో గురుత్వబలం చేసిన పని [Imp.Q]
జవాబు:
a) వాలు తలంపై జారుతున్న వస్తువు విషయంలో గమనదిశకు వ్యతిరేక దిశలో ఘర్షణ బలం పనిచేస్తుంది. అందువలన అక్కడ జరిగిన పని ఋణాత్మకము.

b) జరిగిన పని ధనాత్మకం. ఎందుకనగా గురుత్వబలానికి మరియు స్థానభ్రంశానికి మధ్య అల్పకోణం ఉంటుంది.

ప్రశ్న 6.
ఈ క్రింది సందర్భాలలో బలం వలన జరిగిన పని సంజ్ఞను తెల్పండి.
a) ఒక వస్తువు సమవేగంతో ఘర్షణ ఉన్న క్షితిజ సమాంతర తలంపై చలిస్తూ ఉంటే అనువర్తించిన బలం చేసిన పని
b) కంపిస్తున్న లోలకాన్ని విరామస్థితిలోకి తేవడానికి గాలి నిరోధక బలం చేసే పని
జవాబు:
a) వస్తువు పై పనిచేయుచున్న బలం, వస్తువు స్థానభ్రంశం ఒకే దిశలో ఉన్నవి కావున ఆ బలం వలన జరిగిన పని ధనాత్మకం.

b)గాలి ప్రయోగించు నిరోధ బలం ఎల్లప్పుడూ లోలకము స్థానభ్రంశమునకు వ్యతిరేక దిశలో ఉండును. అందువలన నిరోధ బలం వలన జరిగిన పని ఋణాత్మకం.

ప్రశ్న 7.
ఈ క్రింది ప్రతిపాదనలు సరియైనవో కాదో చెప్పండి. తగిన కారణములను ఇవ్వండి.
a) ఏ అంతర్భలాలు, బాహ్య బలాలు పనిచేస్తున్నప్పటికి ఒక వ్యవస్థ మొత్తం శక్తి నిత్యత్వంగా ఉంటుంది.
b) చంద్రుడు భూమి చుట్టూ ఒక భ్రమణం చేయడానికి భూమి గురుత్వ బలం చేసిన పని శూన్యం.
జవాబు:
a) ఈ ప్రతిపాదన సరియైనదే. వ్యవస్థ వియుక్త వ్యవస్థ (isolated system) అయినపుడు ఆ వ్యవస్థ మొత్తము శక్తి స్థిరముగా ఉండును.
గమనిక: శక్తి యొక్క అన్ని రూపములను గణనలోనికి తీసుకోవలయును.

(b) ఈ ప్రతిపాదన సరియైనదే. గరుత్వాకర్షణ బలం నిత్యత్వ బలం (conservative force). నిత్యత్వ బలం వలన ఒక సంవృత వలయంలో జరిగిన పని శూన్యము.

ప్రశ్న 8.
క్రింది సందర్భాలలో ఏ భౌతికరాశి స్థిరంగా ఉంటుంది? [Imp.Q]
i) స్థితిస్థాపక అభిఘాతంలో
ii) అస్థితిస్థాపక అభిఘాతంలో
జవాబు:
i) స్థితిస్థాపక అభిఘాతాలలో ద్రవ్యవేగం మరియు గతిజశక్తి రెండూ స్థిరంగా ఉంటాయి.

ii) అస్థితిస్థాపక అభిఘాతాలలో కేవలం ద్రవ్యవేగం మాత్రమే స్థిరంగా వుంటుంది.

ప్రశ్న 9.
‘h’ ఎత్తు నుండి స్వేచ్ఛగా క్రిందకు పడిన ఒక వస్తువు చదునైన నేలను తాకిన తరువాత h/2 ఎత్తుకు పైకి లేస్తే ఆ వస్తువుకు, నేలకు మధ్య ప్రత్యావస్థాన గుణకం ఎంత? [TS 18][Imp.Q]
జవాబు:
ఇక్కడ h₁ = h మరియు h₂ = h/2

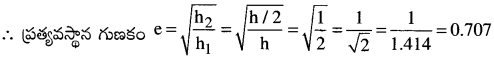
ప్రశ్న 10.
స్వేచ్ఛగా కొంత ఎత్తు నుండి భూమిపై పడ్డ వస్తువు అనేకసార్లు అదేచోట పడిలేచిన తరువాత అభిఘాతాలు ఆగిపోయేలోపు దాని మొత్తం స్థానభ్రంశం ఎంత? వస్తువుకు, భూమికి మధ్య ప్రత్యావస్థాన గుణకం ‘e’ అనుకోండి.
జవాబు:
మొత్తం స్థానభ్రంశం = h. ప్రయాణించిన మొత్తం దూరం = h (\(\frac{1+e^2}{1-e^2}\))

Short Answer Questions (స్వల్ప సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
స్థితిజశక్తి అంటే ఏమిటి ? గురుత్వ స్థితిజశక్తి సమాసాన్ని రాబట్టండి.
జవాబు:

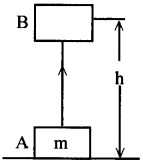
స్థితిజశక్తి :
తన స్థానము లేదా స్థితి వలన కాని వస్తువుకు ఉండే శక్తిని స్థితిజశక్తి అంటారు. ఉదా : రిజర్వాయర్లో గల నీటికి, చుట్టబడిన స్ప్రింగ్కు స్థితిశక్తి ఉంటుంది.

స్థితిశక్తి సమీకరణము :
‘m’ ద్రవ్యరాశి గల వస్తువు భూమిఉపరితలంపై నిశ్చలస్థితిలో ఉంది అనుకొనుము. ఆ వస్తువుపై పనిచేసే బలం దాని భారం mg కి సమానం. ఆ వస్తువును ‘h’ ఎత్తుకు లేవనెత్తడానికి అవసరమయ్యే బలం mg.
జరిగిన పని W = బలము × స్థానభ్రంశము = mg × h = mgh
వస్తువు మీద జరిగిన పని దానిలో శక్తి రూపంలో స్థితిశక్తిగా నిల్వఉంటుంది. కావున పని = P.E
∴ స్థితిశక్తి P.E = mgh

ప్రశ్న 2.
ఒకే ద్రవ్యవేగం కలిగి ఉన్న ఒక లారీ మరియు కార్లను విరామ స్థితికి తీసుకురావడానికి ఒకే బ్రేకు బలాన్ని ఉపయోగించారు. ఏ వాహనం తక్కువ కాలంలో విరామ స్థితికి వస్తుంది? ఏ వాహనం తక్కువ దూరంలో ఆగుతుంది. [Imp.Q]
జవాబు:
లారీ, కారు ఒకే ద్రవ్యవేగంతో చలిస్తున్నాయి మరియు వాటిపై పనిచేసే వ్యతిరేకబలం సమానం.

⇒ F × t = mv – mu ప్రకారం (తొలి వేగం = v, తుది వేగం = 0)
లారీ మరియు కారు తొలి ద్రవ్యవేగాలు mv సమానం. మరియు వానిపై ప్రయోగించిన బ్రేకుల బలాలు (F) సమానం. కనుక t లు కూడ సమానం. అనగా లారీ, కారు ఒకేసారి విరామ స్థితికి వచ్చును.

ప్రశ్న 3.
నిత్యత్వ మరియు అనిత్యత్వ బలాల మధ్య తేడాలను వ్రాయండి. వాటికి ఒక్కొక్క ఉదాహరణ ఇవ్వండి. [Imp.Q]
జవాబు:

నిత్యత్వ బలాలు	అనిత్యత్వ బలాలు
1. సంవృత వలయంలో ఏదైనా బలం వలన జరిగిన పని శూన్యమైతే దానిని నిత్యత్వ బలం అంటారు.	1. సంవృత వలయంలో ఏదైనా బలం వలన జరిగిన పని శూన్యం కాకపోతే దానిని అనిత్యత్వ బలం అంటారు.
2. ఈ బలాల వలన జరిగిన పని, దాని మార్గంపై ఆధారపడదు.	2. ఈ బలాల వలన జరిగిన పని, దాని మార్గంపై ఆధారపడుతుంది.
3. ఉదా || గురుత్వ బలం.	3. ఉదా || ఘర్షణ బలం.

ప్రశ్న 4.
ఏకమితీయ స్థితిస్థాపక అభిఘాతంలో అభిఘాతానికి ముందు రెండు వస్తువుల అభిగమన సాపేక్ష వేగం అభిఘాతం తరువాత వాటి నిగమన సాపేక్ష వేగానికి సమానమని చూపండి? [Imp.Q] [TS 18] [AP 20]
జవాబు:
A మరియు B అనే గోళాల ద్రవ్యరాశులు m₁, m₂ కలిగి, u₁ మరియు u₂ తొలివేగాలతో ప్రయాణిస్తూ అభిఘాతం చెందాయి. వాటి తుది వేగాలు v₁ మరియు v₂ అనుకొనుము.

రేఖీయ ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం
అభిఘాతం ముందు మొత్తం ద్రవ్యవేగం = అభిఘాతం తర్వాత మొత్తం ద్రవ్యవేగం
m₁ u₁ + m₂u₂ = m₁v₁ + m₂v₂
m₁(u₁ – v₁) = m₂(v₂ – u₂) ——–(1)
గతిశక్తి నిత్యత్వ నియమం ప్రకారం.

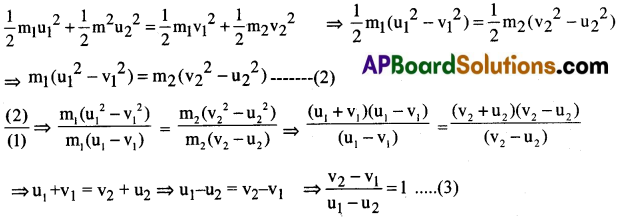
అనగా అభిఘాతం ముందు అభిగమన సాపేక్షవేగం = అభిఘాతం తర్వాత నిగమన సాపేక్షం.

ప్రశ్న 5.
రెండు సమాన ద్రవ్యరాశులు ఏటవాలు స్థితిస్థాపక అభిఘాతం చెందినప్పుడు రెండవ వస్తువు మొదట్లో విరామ స్థితిలో ఉన్నది. అభిఘాతం తరువాత అవి ఒకదానికొకటి లంబంగా చలిస్తాయని చూపండి.
జవాబు:

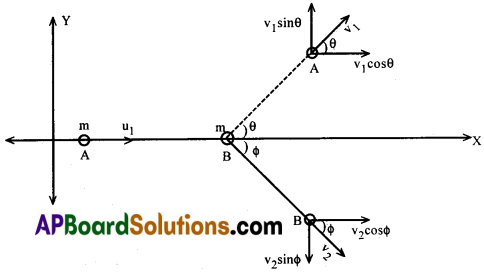
m ద్రవ్యరాశి గల వస్తువు u₁ వేగంతో X- అక్షము దిశలో ప్రయాణించుచూ విరామస్థితిలో ఉన్న m ద్రవ్యరాశి గల B అను వస్తువుతో స్థితిస్థాపక ద్విమితీయ అభిఘాతం జరిపినది అని అనుకొనుము.

అభిఘాతము తరువాత A అను వస్తువు X- అక్షముతో θ కోణం చేయుచూ v₁ వేగంతో చలించుచున్నదను కొనుము. అభిఘాతము తరువాత B అను వస్తువు X- అక్షముతో Φ కోణం చేయుచూ v₂ వేగంతో చలించుచున్నదను కొనుము.

స్థితి స్థాపక అభిఘాతం కనుక గతిశక్తి నియమం ప్రకారం

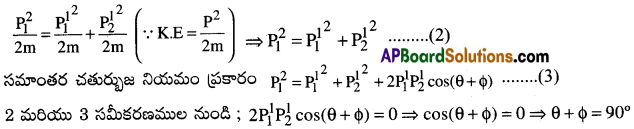
కావున ఆ రెండు వస్తువుల ద్విమితీయ స్థితిస్థాపక అభిఘాతం తరువాత పరస్పర లంబదిశలలో ప్రయాణించును.

ప్రశ్న 6.
కొంత ఎత్తు నుంచి స్వేచ్ఛగా కిందికి పడిన వస్తువు భూమితో ‘n’ అభిఘాతాలు చెందిన తరవాత అది పొందిన ఎత్తుకు సమీకరణాన్ని ఉత్పాదించండి.
జవాబు:
‘h’ ఎత్తు నుంచి ఒక బంతిని నేలపై జారవిడిచామనుకుందాం. బంతి u₁ వేగంతో నేలను ఢీకొని h₁ ఎత్తుకు లేస్తుంది అనుకోండి. అభిఘాతం ముందు అభిఘాతం తరువాత కూడా నేల వేగం శూన్యం (u₂ = v₂ = 0).

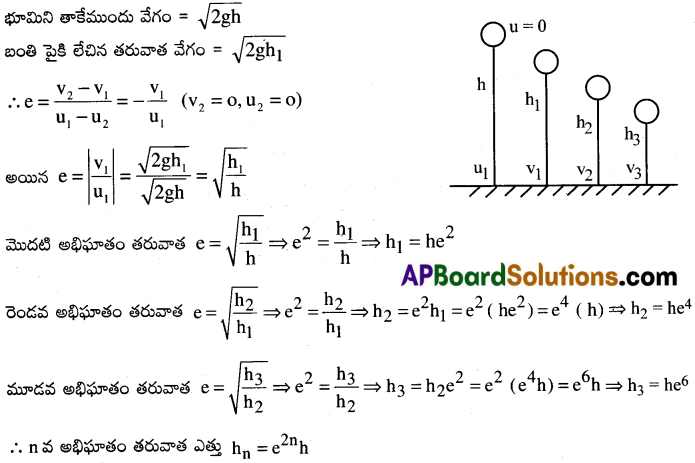
ప్రశ్న 7.
శక్తి నిత్యత్వ నియమును వివరించండి. [Imp.Q]
జవాబు:
ఒక వియుక్త వ్యవస్థ (isolated system) మొత్తము శక్తి స్థిరముగా ఉండును. అనగా వ్యవస్థలో శక్తి ఒక రూపములో నశించిన, అంతే శక్తి వేరొక రూపములలో జనించును. అనగా శక్తిని సృష్టించలేము లేక నశింపచేయలేము.

ఒక వ్యవస్థ యొక్క యాంత్రిక శక్తి వరకు ఆలోచించిన, వ్యవస్థ పై పనిచేయు బలములు నిత్యత్వమైనప్పుడు, యాంత్రిక శక్తి (స్థితిశక్తి + గతిశక్తి) స్థిరముగా ఉండును. కాని వ్యవస్థపై పనిచేయు బలములలో కొన్ని అనిత్యత్వములైనచో, యాంత్రిక శక్తిలోని కొంత భాగము ఉష్ణము, కాంతి, ధ్వని వంటి శక్తి రూపములలోనికి మారవచ్చును. కాని వ్యవస్థ యొక్క మొత్తము శక్తి స్థిరముగా ఉండును.

మొత్తము విశ్వమును ఒక వియుక్త వ్యవస్థగా భావించిన, ఈ విశ్వము మొత్తము శక్తి స్థిరము. విశ్వంలోని ఒక భాగం శక్తిని కోల్పోయిన, ఇంకొక భాగం అంతే శక్తిని గ్రహించును.

Long Answer Questions (దీర్ఘ సమాధాన ప్రశ్నలు)

ప్రశ్న 1.
పని, గతిజశక్తి భావనలను అభివృద్ధి పరచి ఇది పని శక్తి సిద్ధాంతానికి దారితీస్తుందని చూపండి. [AP 17][TS 15, 22]
జవాబు:
పని :
ఒక వస్తువు పై బలం ప్రయోగించినపుడు, బల ప్రయోగదిశలో వస్తువునకు స్థానభ్రంశం ఉన్నపుడు ఆ బలం వలన పని జరిగినది అని అంటారు. ప్రయోగించిన బలం \(\overrightarrow{F}\) వస్తువు స్థానభ్రంశం \(\overrightarrow{S}\) అయితే పని W = \(\overrightarrow{F}.\overrightarrow{S}\)

గతిశక్తి :
ఒక వస్తువునకు తన చలనం వలన సంక్రమించే శక్తిని గతిశక్తి అని అంటారు.
ఉదా : గమనంలో ఉన్న రైలు, ప్రవహించుచున్న నీరు మొదలైనవి. ‘m’ద్రవ్యరాశి గల వస్తువు v వేగంతో చలించుచున్నపుడు
దాని గతిశక్తి = \(\frac{1}{2}\)mv²

పని శక్తి సిద్ధాంతము ఉత్పాదన :
‘m’ ద్రవ్యరాశి కలిగి, తొలివేగం ‘u’ తో చలించే వస్తువుపై ‘F’ అనే స్థిర బలం పనిచేస్తుందని అనుకుందాం. t కాలంలో వస్తువు పొందిన స్థానభ్రంశం S మరియు తుది వేగం ‘ అనుకొనుము.

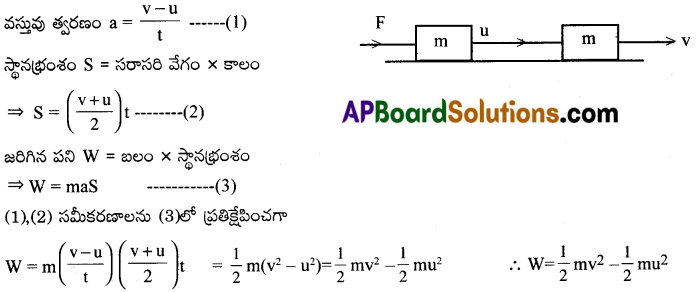
W = తుదిగతిశక్తి – తొలిగతిశక్తి
కావున పనిశక్తి సిద్ధాంతం నిరూపించబడింది.

నియమాలు :
మారుతున్న బలాలతో పనిచేస్తున్న ఒక వ్యవస్థలోని కణాలపై పని-శక్తి సిద్ధాంతం అనువర్తింపచేయవచ్చు.

ప్రశ్న 2.
అభిఘాతములు అనగా ఏమి? అభిఘాతములు ఎన్ని రకములుగా ఉండవచ్చును? ఏకమితీయ స్థితి స్థాపక అభిఘాత సిద్ధాంతమును వివరించండి. [TS 22][AP 19,20,22][Imp.Q]
జవాబు:
అభిఘాతము :
ఇతర బలాల ప్రభావం లేకుండా, రెండు వస్తువుల మధ్య అతి తక్కువ కాల వ్యవధిలో జరిగే అంతర చర్యల వల్ల ద్రవ్యవేగం వినిమయం జరుగుతుంది. దీనినే అభిఘాతం అంటారు.

అభిఘాతములు రెండు రకములు:
(i) స్థితిస్థాపక అభిఘాతం
(ii) అస్థితిస్థాపక అభిఘాతం

(i) స్థితిస్థాపక అభిఘాతం:
ద్రవ్యవేగ నిత్యత్వ నియమం, గతిశక్తి నిత్యత్వ నియమం రెండూ పాటించబడు అభిఘాతములను స్థితిస్థాపక అభిఘాతములు అని అంటారు.
ఉదా : రెండు బిలియర్డ్స్ బంతుల మధ్య అభిఘాతము, వాయు అణువుల మధ్య అభిఘాతములు

(ii) అస్థితిస్థాపక అభిఘాతం:
ద్రవ్యవేగ నిత్యత్వ నియమం పాటించబడి, గతిశక్తి నిత్యత్వ నియమం పాటించబడని అభిఘాతములను అస్థితి స్థాపక అభిఘాతములు అని అంటారు.
ఉదా : బ్యాట్ తో బంతిని కొట్టుట, బుల్లెట్ను చెక్కదిమ్మె లోనికి పేల్చుట.

m₁ ద్రవ్యరాశి గల ఒక గోళం u₁ వేగంతో చలిస్తూ, m₂ ద్రవ్యరాశి కలిగి అదే దిశలో u₂ వేగంతో చలించే మరొక గోళాన్ని ఢీ కొన్నదనుకోండి. అభిఘాతం తర్వాత వాటి వేగాలు వరుసగా v₁, v₂ అనుకోండి.

ఏకమితీయ స్థితిస్థాపక అభిఘాతాలలో ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం
అభిఘాతం ముందు మొత్తం ద్రవ్యవేగం = అభిఘాతం తర్వాత మొత్తం ద్రవ్యవేగం.
⇒ m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂ ⇒ m₁(u₁ – v₁) = m₂(v₂ – u₂) ——–(1)
గతిశక్తి నిత్యత్వ నియమం నుండి

ప్రశ్న 3.
శక్తి నిత్యత్వ నియమమును నిర్వచించి, స్వేచ్ఛగా పడు వస్తువు విషయంలో దానిని నిరూపించండి. [Imp.Q] [AP,TS 15,16,17,18,19,20]
జవాబు:
శక్తి నిత్యత్వ నియమం :
శక్తిని సృష్టించలేము, నాశనం చేయలేము, కాని ఒక రూపంలోని శక్తిని మరొక రూపంలోకి మార్చవచ్చును.
వ్యవస్థ యొక్క మొత్తం శక్తి ఎల్లప్పుడూ స్థిరము.

స్వేచ్ఛాపతన వస్తువు :
‘m’ద్రవ్యరాశి గల ఒక వస్తువు భూమి నుంచి ‘h’ ఎత్తులో ఉండే A అనే బిందువు నుంచి స్వేచ్ఛగా పడుతుంది అనుకొనుము.

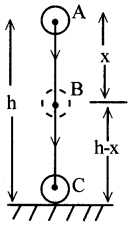
‘A’ బిందువు వద్ద :
స్థితిశక్తి P.E = mgh
A వద్ద వేగం v_A = u = 0
గతిశక్తి K.E = \(\frac{1}{2}\)mv²_A = m(0)² = 0
మొత్తంశక్తి T.E= P.E + K.E = mgh + 0 = mgh …..(1)

‘B’ బిందువు వద్ద :
స్థితిశక్తి P.E = mg(h – x) = mgh – mgx
మరియు B బిందువు వద్ద s = x, u = 0, v = v_B, a = +g
∴ v² – u² = 2as ⇒ v²_B = 2gx
ఇక్కడ K.E = \(\frac{1}{2}\)mv²_B = \(\frac{1}{2}\)m(2gx) = mgx
∴ T.E = P.E + K.E = mgh – mgx + mgx = mgh …….(2)

‘C’ బిందువు వద్ద :
స్థితిశక్తి P.E = mg (0) = 0, ‘C’ బిందువు వద్ద h = 0 కావున
మరియు C బిందువు వద్ద s = h, u = 0, v = v_c, a = +g
∴ v² – u² = 2as ⇒ v² = 2gh

ఇక్కడ K.E = \(\frac{1}{2}\)mv²_C = \(\frac{1}{2}\)m(2gh) = mgh
మొత్తంశక్తి T.E = P.E + K.E = 0 + mgh = mgh …….(3)
(1),(2),(3) ల నుండి మొత్తం శక్తి ‘స్థిరం’ అని తెలియచున్నది.
కావున శక్తి నిత్యత్వ నియమం నిరూపించబడింది.

Solved Problems (సాధించిన సమస్యలు)

ప్రశ్న 1.
బలము \(\overline{\mathrm{F}}=(3\overline{\mathrm{i}}+4\overline{\mathrm{j}}-5\overline{\mathrm{k}})\) ప్రమాణములు మరియు స్థాన భ్రంశము \(\overline{\mathrm{d}}=(5\overline{\mathrm{i}}+4\overline{\mathrm{j}}+3\overline{\mathrm{k}})\) ప్రమాణములు. వీని మధ్య కోణము ఎంత? \(\overline{\mathrm{d}}\) సదిశ దిశలో \(\overline{\mathrm{F}}\) విక్షేపాన్ని కనుక్కోండి.
సాధన:

ప్రశ్న 2.
సైకిలు పై పోవు వ్యక్తి జారుతూ 10 మీటర్ల దూరములో సైకిల్ ను అపివేసెను. ఈ ప్రక్రియలో సైకిల్ మీద రోడ్డు ప్రయోగించిన బలం 200 న్యూ. (a) రోడ్డు సైకిలు పై చేసిన పని ఎంత? (b) సైకిలు రోడ్డు పై చేసిన పని ఎంత?
సాధన:
(a) సైకిలును ఆపుటకు ప్రయోగించబడిన బలము, సైకిలు స్థానభ్రంశమునకు వ్యతిరేకదిశలో ఉండును. అనగా వాని మధ్య కోణము 180°.
కాబట్టి రోడ్డు చేసిన పని W_r = Fd cosθ = 200 × 10 × cos180° = -2000 J

(b) న్యూటను 3 వ గమన నియమం ప్రకారం, సైకిలు రోడ్డు పై 200 న్యూ. బలమును ప్రయోగించును. కాని రోడ్డు స్థాన భ్రంశము చెందదు. కాబట్టి సైకిలు రోడ్డు పై చేసిన పని శూన్యం.

ప్రశ్న 3.
ఒక పోలీసు అధికారి 50 గ్రా. బుల్లెట్ను 200 మీ/సె. వేగంతో ప్రేల్చెను. బుల్లెట్ 2 సెం.మీ. మందము గల చెక్క నుండి బయటకు వచ్చుచున్నప్పటికి దాని గతి శక్తి తొలి గతి శక్తిలో 10% ఉన్నచో చెక్క నుండి బయటకు వెలువడునపుడు దాని వేగం ఎంత? [TS 15]
సాధన:

ప్రశ్న 4.
ఒక లిఫ్ట్ మోయగలిగిన గరిష్ట భారం (లిఫ్ట్ + వ్యక్తులు) 1800 కి.గ్రా. ఆ లిఫ్ట్ 2 మీ/సె. స్థిరవేగంతో పైకి పోవుచున్నది. దాని చలనమును నిరోధించుచున్న బలం 4000 న్యూ. ఒక మోటారు లిఫ్టునకు అందించవలసిన కనీస సామర్ధ్యము ను వాట్టులలోను, అశ్వసామర్థ్యములలోను కనుగొనుము.
సాధన:
లిఫ్టు పై క్రింది దిశలో పని చేయుచున్న మొత్తము బలము F = mg + F_f = (1800 × 10) + 4000 = 22000N
లిఫ్ట్ 2మీ/సె స్థిర వేగంతో పైకి పోవుటకు మోటారు ప్రయోగించవలసిన కనీస బలం, ఈ బలమునకు సమానం. కనుక సామర్థ్యం, P = F.v = 22000 × 2 = 44000 W
మోటారు సామర్థ్యం (అశ్వ సామర్థ్య ప్రమాణములలో) = 59 hp (∵ 1 hp = 746W)

Exercise Problems

ప్రశ్న 1.
10 గ్రాములు ద్రవ్యరాశి గల ఒక పరీక్షనాళికలో కొంత ఈధర్ను 1 గ్రాము ద్రవ్యరాశి గల మూతతో బంధించిరి. పరీక్ష నాళికను వేడిచేసినపుడు ఈథర్ ప్రయోగించు ఒత్తిడితో మూత ఎగిరిపోవును. 5 సెం.మీ పొడవు గల తేలికైన దృఢ కడ్డీతో పరీక్ష నాళికను క్షితిజ సమాంతరముగా వ్రేలాడదీసిరి. దృఢ కడ్డీని ఆధారము చేసుకొని, పరీక్ష నాళిక నిలువు తలములో ఒక వృత్తమును పూర్తి చేయుటకు, మూత ఎంత కనీస వేగంతో పరీక్ష నాళిక నుండి బయటకు రావలయును? ఈథర్ ద్రవ్యరాశిని నిర్లక్ష్యము చేయవచ్చును.
సాధన:
పరీక్ష నాళిక ద్రవ్యరాశి, m_T = 10 గ్రా = 10 × 10^-3 కి.గ్రా
మూత ద్రవ్యరాశి, mc = 1 గ్రా = 1 × 10^-3 కి.గ్రా
కడ్డీ పొడవు = పరీక్ష నాళిక తిరుగు వృత్త వ్యాసార్థము = r = 5 సెం.మీ = 5 × 10^-2 మీ

వేడి చేయుటకు ముందు, పరీక్ష నాళిక మరియు దాని మూత విరామ స్థితిలో ఉండును. కావున వాని తొలి ద్రవ్యవేగము సున్న. ద్రవ్యవేగ నిత్యత్వ నియమం ప్రకారం, వేడి చేసిన తరువాత కూడ వాని మొత్తము ద్రవ్యవేగము సున్నకు సమానముగా ఉండవలయును.
మూత ద్రవ్యవేగం = పరీక్ష నాళిక ద్రవ్యవేగం

ప్రశ్న 2.
ఒక మర తుపాకి నిమిషమునకు 360 బుల్లెట్లను ప్రేల్చును. ఒక్కొక్క బుల్లెట్ వేగము 600 మీ/సె మరియు ద్రవ్యరాశి 5 గ్రా. అయిన మరతుపాకి సామర్థ్యము ఎంత? [TS 18][IPE’ 13, 13][AP 15, 16, 18, 19]
సాధన:
ఒక్కొక్క బుల్లెట్ ద్రవ్యరాశి (m) = 5గ్రా = 5 × 10^-3 కి.గ్రా, ఒక్కొక్క బుల్లెట్ వేగము (v) = 600 మీ/సె
తుపాకి గుండ్ల సంఖ్య (n) = 360; కాలం (t) = 1 నిమిషం = 60 సె; సామర్థ్యం (p) =?

ప్రశ్న 3.
8 మీటర్ల లోతు గల బావి నుండి ఉపరితలమునకు గంటకు 3425 మీ3 నీటిని పైకి తోడుటలో ఒక మోటారు సామర్థ్యములో ఉపయోగపడిన సామర్థ్యము ఎంత? మోటారు అశ్వసామర్థ్యము లో 40% వృధా అయిన దాని అసలు అశ్వ సామర్థ్యం ఎంత?
సాధన:
పైకి తోడిన నీటి ఘన పరిమాణం, v = 3425 మీ³., నీటి సాంద్రత d = 1000 కి.గ్రా/మీ³.
∴ పైకి తోడిన నీటి ద్రవ్యరాశి, m = ఘనపరిమాణంxసాంద్రత= 3425 × 10³ కి.గ్రా
నీరు పైకి వచ్చిన ఎత్తు(h) = 8 మీ, గురుత్వ త్వరణం(g) = 9.8 మీ. సె^-2
1 గంటలో మోటారు పంప్ చేసిన పని = mgh
= 3425 × 10³ × 9.8 × 8 = 268520 × 10³J

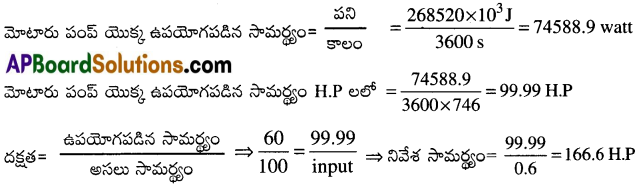
ప్రశ్న 4.
25 మీటర్ల లోతు గల బావి నుండి నిమిషమునకు 600 కి.గ్రా. ద్రవ్యరాశి గల నీటిని తోడి ఆ నీటిని 50 మీ/సె. వేగంతో బయటకు వదులుటకు ఒక మోటారు పంపనకు కావలసిన సామర్థ్యం ఎంత? [AP 15,18][TS 16,19,20,22]
సాధన:
బయటకు తోడవలసిన నీటి ద్రవ్యరాశి (m) = 600 కి.గ్రా
బావి లోతు (h) = 25 మీ
నీటిని పైకి తోడుటకు మోటారు చేయు వలసిన పని(W₁) = mgh = 600 × 9.8 × 25 = 147000 J
నీటి వేగము (v) = 50 మీ. సె^-1
నీటి ద్రవ్యరాశి(m) = 600 కి. గ్రా
నీటికి గతిశక్తి నిచ్చుటకు మోటారు చేయవలసిన పని, w₂ = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 600 × 2500 = 750000 J
మొత్తము చేయవలసిన పని, w = w₁ + w₂ = 147000 + 750000 = 897000J
కాలం (t) = 1 నిమిషం 60 సె.

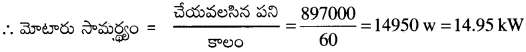
ప్రశ్న 5.
ఒక నిరూపక వ్యవస్థ మూల బిందువు వద్ద 5 కి.గ్రా. ద్రవ్యరాశి గల వస్తువు విరామస్థితిలో ఉన్నది. దానిపై F = (20 + 5x) న్యూ. బలం ధన X- అక్షము దిశలో పనిచేయుచున్నది. అయిన ఆ వస్తువును x = 0 నుండి x = 4 మీ దూరము వరకు జరుపుటకు ఆ బలం చేయవలసిన పని ఎంత?
సాధన:
వస్తువు ద్రవ్యరాశి (m) = 5 కి.గ్రా
వస్తువు పై బలం (F) = (20 + 5x) న్యూ
వస్తువును dx అను స్వల్ప దూరమును జరుపుటకు చేయవలసిన పని dw = Fdx
∴ x = 0 నుండి x = 4 వరకు వస్తువును జరుపుటకు చేయవలసిన మొత్తము పని

ప్రశ్న 6.
పటములో చూపినట్లు 5 కి.గ్రా. ద్రవ్యరాశి గల ఒక దిమ్మె నునుపైన వాలు తలము పై నుండి జారుచున్నది. వాలు తలము క్రింది చివరన అమర్చిన స్ప్రింగ్ యొక్క బలస్థిరాంకము 600నూ/మీ. దిమ్మె వేగము కనిష్టమగు సమయములో స్ప్రింగ్ లోని సంపీడ్యము ఎంత?
సాధన:
దిమ్మె ద్రవ్యరాశి m = 5 కి.గ్రా, K = 600 న్యూ/మీ, g = 10 మీ/సె², స్ప్రింగ్లోని సంపీడ్యము x =?

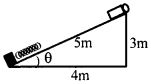
పటము నుండి, sinθ = 3/5
న్యూటను మూడవ గమన నియమం ప్రకారం,
దిమ్మె స్ప్రింగ్ పై ప్రయోగించు బలం F_B
= – స్ప్రింగ్ లోని పునః స్థాపక బలం F_R
F_B = F_R ⇒ mgsinθ = Kx.
⇒ 5 × 10 × \(\frac{3}{5}\) = 600 × x
⇒ 5 × 10 × \(\frac{3}{5}\) = 600 × x ⇒ x = \(\frac{30}{600}\) = 0.05m = 5cm

ప్రశ్న 7.
F = –\(\frac{K}{x^2}\)(x ≠ 0) అను బలము ఒక కణము పై X అక్షము దిశలో పని చేయుచున్నది. ఆ కణమును x = +a నుండి x = +2a వరకు స్థానభ్రంశము చెందించుటలో ఆ బలం చేసిన పని ఎంత? K ఒక ధనాత్మక స్థిరాంకము అనుకొనుము.
సాధన:

ప్రశ్న 8.
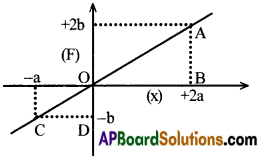
కణము స్థానము X తో కణము పై పనిచేయు బలం F మారు విధానము గ్రాఫ్ చూపబడినది. కణమును x = +a నుండి x = +2a వరకు స్థానభ్రంశము చెందించుటకు బలం చేయు పని ఎంత?

సాధన:
బలం చేసిన పని = x అక్షమునకు, f-x రేఖకు మధ్య గల వైశాల్యము
= OAB త్రిభుజ వైశాల్యము + OCD త్రిభుజ వైశాల్యము
= \(\frac{1}{2}\)× OB × AB – \(\frac{1}{2}\)× OD × CD (బలం దిశ వ్యతిరేకమయినది)
= \(\frac{1}{2}\)× 2a × 2b – \(\frac{1}{2}\) × b × a = 2ab – \(\frac{ab}{2}=\frac{3ab}{2}\)

ప్రశ్న 9.
క్షితిజ సమాంతర తలము నుండి 20 మీటర్ల ఎత్తుగల బిందువు వద్ద నుండి ఒక బంతిని 20 మీ/సె. వేగంతో నిట్టనిలువుగా క్రిందికి విసిరిరి. బంతి నేలను తాకి మరల 20 మీ. ఎత్తునకు లేచినది. అయిన క్షితిజ సమాంతర తలమునకు, బంతికి ‘మధ్యగల ప్రత్యవస్థాన గుణకము ఎంత? (g = 10m/s²)
సాధన:
క్రిందికి వచ్చున్నపుడు బంతి తొలి వేగం, u = 20 మీసె^-1.
బంతి నేలను తాకు లోపల ప్రయాణించు దూరం, s = h = 20 మీ
బంతి నేలను తాకునపుడు వేగం, u₁ = ?

బంతిని మొదటి వస్తువుగా నేలను రెండవ వస్తువుగా భావించుము. బంతికి, నేలకు జరిగిన అభిఘాతములో, అభిఘాతమునకు ముందు మరియు తరువాత నేల విరామస్థితిలో ఉండును. అభిఘాతమునకు ముందు బంతిదిశ, అభిఘాతము తరువాత బంతి దిశకు వ్యతిరేకముగా ఉండును.

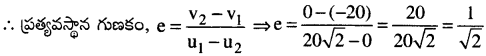
ప్రశ్న 10.
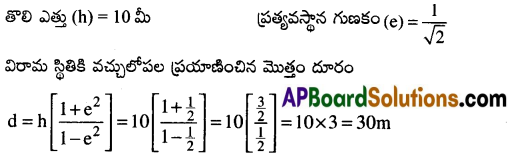
ఒక బంతి 10 మీటర్ల ఎత్తు నుండి ఒక క్షితిజ సమాంతర గట్టి ఉపరితలము పై పడి అనేక సార్లు పైకి, క్రిందికి ప్రయాణించినది. ఆ తలముల మధ్య ప్రత్యవస్థాన గుణకం 1/√2 అయిన బంతి విరామ స్థితికి (అనగా పైకి లేవకుండ) వచ్చు లోపల ప్రయాణించిన దూరం ఎంత?
సాధన:

ప్రశ్న 11.
కొంత ఎత్తు నుండి స్వేచ్ఛగా క్రిందికి పడుతూ ఉన్న 5 kg ద్రవ్వరాశి గలవస్తువు భూమి నుండి 10 m ఎత్తులో ఉన్నపుడు నిలువుగా క్రిందికి 20 m/s వేగం ఉన్న సందర్భంలో ఆ వస్తువు యొక్క మొత్తం శక్తిని కనుక్కోండి. (గురుత్వ త్వరణం 10 m/s² గా తీసుకోండి). [TS 16]
సాధన:
వస్తువు యొక్క ద్రవ్యరాశి(m) = 5kg; వస్తువు యొక్క ఎత్తు (h) = 10m
వస్తువు యొక్క వేగం (v) = 20m/s, గురుత్వ త్వరణం (g) = 10 m/s
స్థితిజ శక్తి = mgh = 5 × 10 × 10 = 500 J
= -×5 × 400=1000J
గతిజ శక్తి = \(\frac{1}{2}\)mv² = \(\frac{1}{2}\) × 5 × (20)² = \(\frac{1}{2}\)× 5 × 400 = 1000J
∴ మొత్తం శక్తి = స్థితిజ శక్తి + గతిజశక్తి = 500 + 1000 = 1500J